Judgment and Decision Making, vol. 7, no. 1, January 2012, pp. 1-18

In this paper, we document a violation of normative and descriptive models of decision making under risk. In contrast to uncertainty effects found by Gneezy, List and Wu (2006), some subjects in our experiments valued lotteries more than the best possible outcome. We show that the overbidding effect is more strongly related to individuals’ competitiveness traits than comprehension of the lottery’s payoff mechanism.

Keywords: Decision making under risk, competitiveness, lottery payoff comprehension, experiments.

1  Introduction

Decision making often involves choices between risky outcomes. Prospect theory and expected utility theory both posit that individuals balance outcomes and their (potentially weighted) probability of occurrence, which means that the certainty equivalent of a binary lottery will lie somewhere between the lowest and the highest outcomes. However, Gneezy, List and Wu (2006) document cases where individuals value a risky prospect less than its worst possible realization. They call this phenomenon the uncertainty effect and demonstrate its existence in various laboratory experiments (including real and hypothetical pricing tasks and inter-temporal choice tasks) as well as in a field experiment (a sportscard market). The uncertainty effect, however, disappears in within-subject designs and is observed only in lotteries that do not involve cash. The Gneezy, List and Wu (2006) study has sparked a small but growing literature examining the robustness of their findings. For example, Sonsino (2008) has found the occurrence of uncertainty effect in an internet-based, within-subject design. Keren and Willemsen (2009) argued, however, that Gneezy, List and Wu’s (2006) results were an artifact of poorly understood experimental instructions. Specifically, in a series of experiments, they replaced the lottery with a coin toss and a spinner wheel to clearly define payoff probabilities. They also added comprehension checks. Their new protocols eliminated the uncertainty effect almost completely. Similarly, Rydval et al. (2009) used physical lottery formats (i.e., drawing a good, a gift exchange or a deferred payment, from a closed bag containing two goods that are identical except for their face value) instead of verbal lottery descriptions and observed that the uncertainty effect almost disappeared.

On the other hand, Simonsohn (2009) argued that the uncertainty effect is neither caused by the fact that Gneezy, List and Wu’s (2006) manipulation of uncertainty was fully confounded by the number of outcomes presented to subjects nor that subjects may had erroneously believed that the lottery could result in a payment of $0. Instead, he argued that the uncertainty effect occurs as a consequence of direct risk aversion. Direct risk aversion arises from a literal distaste for uncertainty; i.e., uncertainty enters directly into people’s utility function.

Theoretically, Gill and Stone (2010) have showed that the uncertainty effect can arise in tournaments where two agents are competing to win a fixed monetary prize. Similarly, Andreoni and Sprenger (2010) argued that the uncertainty effect is not anomalous if certain and uncertain consumption is evaluated with different utility parameters. They argue that marginal utility for uncertain consumption diminishes more quickly than marginal utility for certain consumption. Because uncertain utility is more concave than certain utility, one can expect a gamble to be valued less than its worst possible outcome.

In this paper, we document cases of the polar opposite of the uncertainty effect found in Gneezy, List and Wu (2006), where individuals value the outcome of a risky prospect more than its best possible realization.¹ We demonstrate cases where subjects are willing to pay as much as three times the value of the best possible realization of a lottery in a second price auction. We term this effect the overbidding effect.² In addition to documenting the overbidding effect, we seek to identify the causes of the effect. Three non-exclusive possible explanations of the results we observe are 1) confusion about the auction mechanism 2) confusion or failure of comprehension about lotteries (i.e. subjects did not understand the payoff mechanism of a lottery), and 3) subjects derive utility from winning and being the “top dog” of the experiment (i.e. to walk out of the experiment as the “top dog” among their peers) (Shogren, et al., 2001). Regarding the first two issues, Plott and Zeiler (2005) show that the often-reported WTP-WTA disparity is likely a result of subjects’ confusion with the elicitation mechanism—suggesting that the WTP-WTA divergence is not an underlying feature of preference per se but rather a result of misunderstanding with the bidding mechanism.

It is tempting to attribute the overbidding effect to elements of the value elicitation mechanism. For example, in Kagel and Levin’s (1993) non-risky induced value experiments, subjects tended to slightly overbid in a second price auction. In these experiments, subjects are assigned a value, v, and the winner of the auction is paid the difference between his or her value and the second highest bid, which is the price: profit = v – price. In a second price auction, an individual’s weakly dominant strategy is to submit a bid equal to v, but as Kagel and Levin show, many people submit bids higher than v. Kagel and Levin (1993) attributed overbidding to either the dominant bidding strategy not being transparent or to weak learning feedback mechanisms in the second price sealed bid auction. Although this result is often taken as a stylized fact associated with second price auctions, Lusk and Shogren (2007) document that several more recent induced value studies that focus on all bidders’ values (not just the market price) tend to find behaviour more in-line with theoretical predicted bidding behaviour in the second price auction. Even if we accept the Kagel and Levin’s (1993) result of over-bidding in the second price auction, it is difficult to conclude that this is the primary cause of the behaviour observed here with lotteries where subjects’ values, v, are unknown. Although subjects in our experiments “overbid”, we would expect people’s bids to lie somewhere close to the expected payoff, not close to the maximum payoff of the lottery. Stated differently, the overbidding effect observed by Kagel and Levin (1993) might explain bids slightly higher than the expected value of the lottery but it cannot explain bids in excess of the maximum lottery payout.

We use an experimental design that varied the amount of training about the auction mechanism and amount of feedback after each round. Varying the amount of training allows us to directly test whether confusion with the elicitation mechanism may explain the observed results. On the other hand, the amount of feedback after each round allows us to test whether the mechanism may have induced more competitiveness to the sessions. We also measured subject’s personal traits regarding comprehension of how lotteries work as well as their competitiveness. Our results suggest that the overbidding effect can, in small part, be attributed to comprehension of how lotteries work, but that extensive training with the second price auction does not eliminate the overbidding effect, thus ruling out confusion with the elicitation mechanism as the primary cause of the overbidding. We find that comprehension is negatively related to the overbidding effect while competitiveness traits are positively related to overbidding behavior.

This paper is structured as follows: The next section discusses the design of our auction experiments followed by the data analysis and results. The last section contains the conclusions.

2  Experimental design

A lab experiment was conducted using the z-Tree software (Fischbacher, 2007). Subjects consisted of undergraduate students at Agricultural University of Athens in Greece. During the recruitment, the nature of the experiment and the expected earnings were not mentioned.

We used a 2^nd price Vickrey auction to determine the selling price of the lotteries. A 2x2 design was adopted varying the extent of training (minimal vs. extensive training) and posting of market clearing prices (posting vs. no posting of the 2^nd highest price). Each subject participated in only one treatment. The size of the groups varied from 17 to 18 subjects per treatment. Each treatment lasted no more than an hour. In total, 71 subjects participated in our experiments, which were conducted in March 2009.

Each session included four phases: the training phase, the choice task, the lottery auction phase and the post-experimental phase. Data from the choice task are analyzed elsewhere (Corrigan, et al., 2012). Subjects were given prior instructions on the overall layout of the session and were also reminded on the procedures at the beginning of each phase. Appendix C displays the experimental instructions for the full training and posted prices treatment. The instructions for the other treatments were adjusted accordingly.

2.1  The training phase

---

Table 1: Lotteries used in the experiment.

Bet pair	Lottery	Bet type	Probability of win	Amount of win	Probability of loss	Amount of loss	Expected payoff
1	A	P-bet	90%	4	10%	1	3.50
	B	$-bet	28%	16	72%	1.5	3.40
2	C	P-bet	80%	3	20%	1	2.20
	D	$-bet	24%	12	76%	1	2.12
3	E	P-bet	75%	2	25%	1	1.25
	F	$-bet	18%	9	82%	0.5	1.21

---

After arriving at the lab, subjects were randomly seated in front of a computer. Subjects were given fifteen Euros (15€) fee at the end of the experiment for their participation. We emphasized that although they were not given the money at the beginning of the experiment, the 15€ was theirs to use as they please and that they should think that they have this money already. To control for possible monetary endowment effects, subjects were also told that a random amount of money between 0.5€ and 3€ was going to be randomly assigned to each one of them.³ Everyone then received this random fee, which was added to their participation fee, as soon as the computerized phase of the experiment began. We emphasized to the subjects that the endowment they received was private information and that they should not communicate this information to other subjects in the lab. All transactions were completed at the end of the experiment. No information about this additional endowment was given during recruitment.

Subjects were then shown a short presentation about how the auctions work to familiarize them with the procedure. All instructions were in PowerPoint and were projected onto a screen in the front of the lab. The instructions emphasized that the subjects should not communicate with each other. Subjects were given an introduction and description about how the 2^nd price Vickrey auction works, a short example on how bids are sorted in a descending order and on how the 2^nd highest bid and the winner are selected. In addition, a numerical example was given to clearly show to subjects why it is in their best interest to bid exactly the amount the product is worth to them and to demonstrate the incentive compatibility of the auction. Subjects were then asked to take a short computerized test regarding the procedure composed of six true or false questions. Most subjects answered five or more questions correctly and only a handful answered as few as four out of six questions correctly. Correct answers were presented on subject’s screen after everyone completed the test. Given that the questions and answers were read aloud and thoroughly explained to subjects, we believe that any misunderstandings about the elicitation mechanism were cleared out before we moved to the next stage of training.

The set of instructions included a short section on what the subjects will see on their computer screen to familiarize them with the computerized part of the experiment. Instructions were also given on how subjects should submit their bids in the appropriate fields of their screen. We did not include a computer-training phase: all the subjects were students and already had computer experience.

We then provided subjects training on the second price auction mechanism. The first part of the training included five hypothetical multi-product⁴ auction rounds. We emphasized to the subjects that these rounds were intended to familiarize them with the auction procedure and although they would not have to pay any money to buy any product they should bid as if they were in a real auction and as if they really intended to buy the product. We also told them that one round and one product would be randomly chosen at the end of these rounds as binding. A screen with subjects’ hypothetical payoffs was displayed after these rounds.

In the second part of the training, we included five real multi-product auction rounds. The products we used were a Tobleron chocolate, a pack of Soft Kings cookies and Kraft’s Lacta chocolate. We emphasized to the subjects that these rounds were real and that if they chose to buy a product they would actually have to pay for it. Similar to the previous hypothetical rounds, one round and one product were randomly chosen as binding at the end of these rounds. A screen with subjects’ payoffs was displayed after these rounds. This procedure demonstrated to subjects that their bidding behavior could determine whether they would end up buying the product or not and that there is a cost associated with not revealing true values. Therefore, subjects experienced the cost of their decision during the experiment early on.

Subjects who participated in the minimal training treatment were not exposed to the full training as described above.⁵ Subjects in the minimal training treatment were not provided with a numerical example on how a 2^nd price auction works, were not given a computerized test and were not explicitly informed about the incentive compatibility of the auction. They also participated only in the hypothetical rounds, not in the real ones.

2.2  The choice phase

After the training phase, subjects made binary choices between lotteries. We asked subjects to indicate their preference for each of three pairs of lotteries with the understanding that each pair has an equal chance of being randomly selected as binding and that their decision or choice in each pair will be applied. Subjects were also informed that at the end of the choice phase and the lottery auction phase, a randomly generated number by the computer would determine which of the two phases would be selected as binding. Subjects during the training phase were shown numerical examples on what exactly would happen depending on the payoff of the lottery under winning and losing scenarios.

The three pairs of lotteries with their corresponding chances and expected payoffs are exhibited in Table 1. To avoid any order effect, bet pairs and lotteries in each pair were randomly shown in each subject’s screen.

Bet pairs 1 and 3 were adopted from Cox and Grether (1996).⁶ Bet pair 2 was added as a medium expected payoff category to the high and low expected payoff lotteries of Cox and Grether (1996). Notice that for bet pair 1, the bad outcome for the $-bet is worse than that for the P-bet.⁷ The opposite exists for bet pair 3, while for bet pair 2, the bad outcomes are equal.

The choice task is not used or analyzed in this paper and is not central in analyzing the overbidding effect that we observe. The choice task was used to explore the issue of preference reversals.⁸ Preference reversal studies typically ask subjects to choose between pairs of lotteries (e.g., lottery A vs. lottery B) and then ask subjects to price lotteries in an auction type mechanism. Ideally if a person chooses A over B in a choice task s/he should also price lottery A higher than lottery B, otherwise we observe a preference reversal. Preference reversal studies in the literature follow this exact sequence of tasks. A natural question that emerges is whether this specific order of tasks (i.e., having the choice task before the pricing task) affects the subsequent pricing task. The short answer is “no”. This has been examined by several studies in the literature (e.g., Grether & Plott, 1979, Hamm, 1979). If an order effect was present, this would be problem for tasks that are of a similar nature (e.g., Harrison, et al., 2005, Holt & Laury, 2002, Holt & Laury, 2005). Even if we assume the extreme position that an order effect exists this should not affect the importance our finding. There is still no plausible theory of preferences which can explain bidding more than the maximum value of a binary lottery.

In addition, the choice task does not give us any insight into the question we are asking: do people “overbid”? All we know is whether people chose one lottery over another. This does not tell us anything about whether people “overbid” because a choice of one lottery over another can always be explained by a particular preference (or level of risk aversion). Thus, the choice task data are not relevant for explaining the overbidding behavior we observe in our data.

2.3  The lottery auction phase

In the lottery auction phase, we presented subjects with the same six lotteries and asked subjects to indicate how much, if any, they were willing to pay to buy each of the lotteries. The appearance of the lotteries was ordered randomly for each subject and valuation was performed simultaneously for all lotteries and not sequentially.⁹ Subjects repeated the bidding task for ten consecutive rounds and were informed that if the lottery auction phase was chosen as binding, only one lottery and one round would then be randomly chosen as binding. In the treatment with posted market clearing prices, subjects were able to observe the 2^nd highest price and winner’s ID (which could not identify the winner since these were anonymously assigned by the computer), while in the no posted market clearing prices treatment, subjects were observing only the winner’s ID.

---

Table 2: Mean, median and maximum bids by rounds.

		Rounds
Lottery		1	2	3	4	5	6	7	8	9	10
A	Mean	1.54	1.96	2.17	2.29	2.25	2.35	2.31	2.29	2.42	2.39
	Median	1.00	1.70	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00
	Maximum bid	5.00	5.00	5.00	5.00	5.00	5.40	5.80	6.00	6.80	7.00
	% of overbidders	4.23	1.41	2.82	9.86	15.5	14.08	12.68	14.08	15.49	14.08
B	Mean	1.28	1.96	2.26	2.55	2.83	2.94	3.29	3.19	3.57	3.36
	Median	0.80	1.50	1.50	2.00	2.00	2.00	2.80	2.00	3.00	2.00
	Maximum bid	10.00	8.00	8.99	8.99	10.00	10.00	11.00	11.00	15.99	15.50
	% of overbidders	0	0	0	0	0	0	0	0	0	0
C	Mean	1.02	1.29	1.46	1.50	1.55	1.65	1.68	1.67	1.70	1.79
	Median	1.00	1.00	1.20	1.10	1.10	1.20	1.50	1.49	1.50	1.50
	Maximum bid	3.00	3.50	4.00	4.00	5.00	6.00	6.80	5.00	5.69	6.10
	% of overbidders	0	2.82	2.82	4.23	9.86	12.68	11.27	12.67	14.08	12.68
D	Mean	1.21	1.72	1.88	2.43	2.62	2.82	2.85	3.06	3.16	2.99
	Median	1.00	1.50	1.30	2.00	2.00	2.00	2.00	2.00	2.00	2.00
	Maximum bid	10.00	7.00	7.50	8.00	9.00	9.00	9.00	10.00	11.99	11.90
	% of overbidders	0	0	0	0	0	0	0	0	0	0
E	Mean	0.61	0.91	0.99	0.99	1.05	1.05	1.09	1.14	1.25	1.26
	Median	0.50	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	Maximum bid	2.00	2.56	2.50	2.98	5.00	3.55	4.39	4.76	5.99	6.23
	% of overbidders	0	2.82	5.63	7.04	11.27	7.04	5.63	9.86	11.27	11.27
F	Mean	0.97	1.42	1.76	1.94	2.18	2.47	2.52	2.59	2.76	2.57
	Median	0.50	1.00	1.60	1.50	1.90	2.00	1.50	1.90	2.00	1.50
	Maximum bid	8.00	6.00	7.00	7.00	7.00	7.30	7.10	10.00	9.00	10.00
	% of overbidders	0	0	0	0	0	0	0	1.41	0	1.41

---

2.4  The post-experimental phase

---

Table 3: Number of overbidders by rounds.

	Rounds
	1	2	3	4	5	6	7	8	9	10
Overbid for 1 lottery	3	5	5	7	8	3	3	6	6	3
Overbid for 2 lotteries	0	0	0	1	3	3	3	3	4	2
Overbid for 3 lotteries	0	0	1	2	4	5	4	5	5	7
Total	3	5	6	10	15	11	10	14	15	12

---

After the experiment, we collected standard socio-demographic information about subjects’ age, household size and economic position of their household (evaluated at a 5-likert scale) and also interviewed the subjects about their comprehension of the lottery’s payoff and their competitiveness traits. Specifically, we asked subjects four questions to assess their comprehension of a lottery’s payoff. The purpose was to investigate if subjects understood lottery payoffs and to assess if they were bidding out of confusion in the auction phase. We asked subjects to imagine themselves in a situation where they are given a lottery with 78% probability of winning 6€ and 22% probability of losing 2€. We then asked subjects to indicate the maximum payoff and the maximum loss of this lottery. We also asked subjects their overall profit (loss) if they bought this lottery for 4€ and then won (lost) the lottery. These questions were given in random order to each subject. We then summed up the correct answers to derive a “comprehension score” for each individual.

Another set of questions was provided to subjects aimed at determining their competitiveness trait. We adopted the scale developed by Brown, Cron and Slocum (1998). We asked subjects to indicate if they agree or disagree with four statements (given in random order) on a 7-point scale ranging from totally disagree to totally agree. A competitiveness score was created by summing people’s answers to the following four statements: (a) I enjoy working in situations involving competition with others; (b) It is important to me to perform better than others on a task; (c) I feel that winning is important in both work and games; and (d) I try harder when I am in competition with other people.

3  Results

Out of the six lotteries auctioned, subjects bid more than the maximum (but uncertain) outcomes for lotteries A, C, E and F (with maximum payoffs of 4€, 3€, 2€ and 9€ respectively, see Table 1).¹⁰ We did not observe similar behavior, however, for lotteries B and D (with maximum payoffs of 16€ and 12€ respectively, see Table 1). Table 2 shows the mean, median and maximum bid by round for the six lotteries. It also exhibits the percentage of subjects overbidding by round and lottery.¹¹ As evident in the table, the mean bid is increasing through the rounds, mainly due to some subjects bidding high for the lotteries. The median bid is relatively constant across rounds.

Overbidding behavior was simultaneously observed for multiple lotteries. Table 3 shows the number of overbidders for 1, 2 and 3 lotteries in any given round. Overbidding tended to begin for one lottery in the early rounds but then became more prevalent for other lotteries as the number of rounds increased.

Table 4 shows the number of distinct overbidders per round (this is the same as the row total in Table 3) and the total number of overbids in each round (aggregated over all lotteries). Note that when these figures deviate from each other, it is an indication that the extra overbids come from the same subjects that overbid on multiple lotteries. As shown in this table, subjects also tend to overbid for more than one lottery as the rounds progress. This can be seen in the third row of Table 4, which shows the ratio of total overbids over distinct overbidders (TMO/DMO). In the first two rounds, subjects-overbid for just one lottery out of six (ratio equals 1) while in the 10^th round, subjects overbid on average for more than two lotteries.

---

Table 4: Number of overbidders and overbids by rounds.

	Rounds
	1	2	3	4	5	6	7	8	9	10
Distinct overbidders (DMO)	3	5	6	10	15	11	10	14	15	12
Total overbids (TMO)	3	5	8	15	26	24	21	27	29	28
Ratio TMO/DMO	1.00	1.00	1.33	1.50	1.73	2.18	2.10	1.93	1.93	2.33

---

---

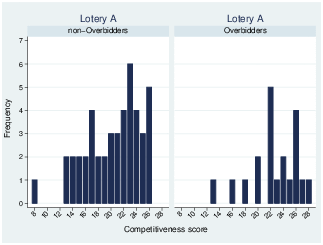
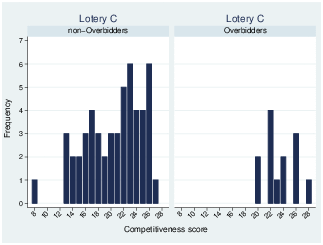
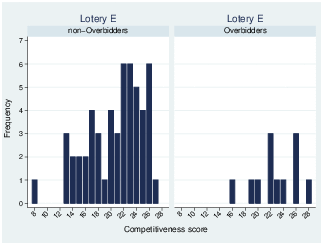
Figure 1: Distribution of competitiveness scores by bidder type

---

---

Figure 2: Distribution of comprehension scores by bidder type.

---

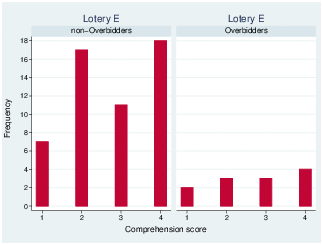
Table 5 shows the number of new overbidders (based on their id’s and aggregated over lotteries) that are added in every round. Results indicate that up to round 5, new subjects tend to imitate the overbidding behavior of subjects from earlier rounds. Hence, it appears that five rounds in our experiments are sufficient for the overbidding effect to arise and stabilize. In all, the documented overbidding behavior is caused by roughly one third (25 subjects) of the subjects in our experiments.

To explore why subjects tend to bid higher than the best possible outcome of the lotteries, we created dummy variables taking the value of one when a subject bid more than the best outcome of a lottery. Figures 1a, 1b, and 1c show the distribution of competitiveness scores for lotteries A, C, and E by bidder type where a subject is defined as an overbidder if s/he bids more than the maximum payoff of the lottery in at least one round. It is apparent that overbidders are on the right end of the distribution, implying that subjects with higher competitiveness traits are more likely to overbid.

Figures 2a, 2b, and 2c show the distribution of comprehension scores. Based on these results, we cannot claim that subjects overbid because they did not understand how the lottery mechanism works since subjects with good comprehension of the lottery mechanism (i.e., scores of 3 or 4) were also likely to overbid.

Table 6 shows the biserial correlation coefficients between the dichotomous variable that depicts whether a subject is an overbidder or not and the corresponding competitiveness and comprehension measures. There are positive medium sized correlations between the dichotomous variable and competitiveness traits. The correlation coefficients with the comprehension variable are negative and relatively lower in magnitude (especially for lottery E).

Table 7 shows correlation coefficients between the cumulative number of overbids across the ten rounds and the competitiveness/comprehension measures. Competitiveness traits exhibit positive correlations with the cumulative number of overbids across the ten rounds while comprehension of the lottery mechanism exhibits negative correlation with the number of overbids.

To further explore the role of treatment variables, namely posting of prices and extensive training, on overbidding behavior, we also calculated the correlation coefficients between the treatment variables and a dichotomous variable indicating whether a subject overbid (tetrachoric correlations) and between the treatment variables and the cumulative number of overbids (biserial correlations) (see Table 8). Results suggest that extensive training is positively and more strongly correlated with the overbidding effect than posting of prices. Therefore, it appears that both treatment variables can exacerbate the overbidding effect.

Similar conclusions can be drawn when we run regression models where we control for several predictors. This analysis is exhibited in Appendix B.

4  Conclusion

In this paper, we document violations in individuals’ valuation of risky prospects. Subjects in our experiments valued some lotteries more than the best possible outcome of the lotteries (i.e., overbidding effect). In some cases this can be as much as three times the maximum payoff of the lottery. Our results generally suggest that as the value of a risky prospect increases, the likelihood of observing an overbidding effect decreases. In addition, we do not observe an overbidding effect in lotteries with higher maximum payoffs (i.e., lotteries with maximum payoffs more than 9€). Our results also suggest that the probability of observing an overbidder’s effect is negatively related to the value of the maximum winning outcome and positively related to the likelihood of winning (see regression results in the Appendix).

In this paper, we also showed that the overbidding effect is more correlated with individuals’ competitiveness traits than with comprehension of the lottery’s payoff mechanism. Specifically, we find that competitiveness is positively related to overbidding behavior while comprehension is negatively related to the overbidding effect. That competitiveness influences bids tends to suggest that the overbidding effect may be an artifact associated with eliciting values using auction-type elicitation mechanism rather than a fundamental feature of people’s preferences. However, we cannot rule out this latter case as it appears that characteristics of the lottery (not just characteristics of the individual) also influence the extent of overbidding. Our results also suggest the possibility that confusion about how lotteries work (rather than with the elicitation mechanism) may be a reason for anomalous behaviour frequently observed in decision making under risk. We also showed that clearing out subject’s misconceptions about the elicitation mechanism exacerbated overbidding, thus ruling out failure of comprehension of the mechanism as a primary cause of the effect.

Our findings imply that, for experiments that involve risky prospects, we should try not only to interpret the results in light of the behavioral theories that have been advanced regarding how people value risky prospects, but also to develop theories on how people understand lotteries. We should also attempt to further examine how the environments created by the elicitation mechanisms themselves (rather than “true” underlying references) may cause certain types of anomalous behavior.

---

Table 5: Number of new overbidders by rounds.

	Rounds										Total
	1	2	3	4	5	6	7	8	9	10
Number of new overbidders	3	4	3	5	8	0	0	1	1	0	25

---

---

Table 6: Biserial correlation coefficients for overbidders by lottery. (Standard errors in parenthesis.)

	Lottery A	Lottery C	Lottery E
Competitiveness	0.242 (0.058)	0.298 (0.052)	0.290 (0.061)
Comprehension	−0.196 (0.066)	−0.258 (0.064)	−0.080 (0.081)

---

References

---

Table 7: Pearson correlation coefficients for number of overbids by lottery. (Standard errors are in parenthesis.)

	Lottery A	Lottery C	Lottery E
Competitiveness	0.187 (0.121)	0.192 (0.120)	0.166 (0.122)
Comprehension	−0.161 (0.122)	−0.188 (0.121)	−0.049 (0.125)

---

---

Table 8: Tetrachoric and biserial correlations by treatment variables and lottery. (Standard errors in parentheses.)

		Lottery A	Lottery C	Lottery E
Overbidders	Prices posted	0.173 (0.080)	0.272 (0.084)	0.280 (0.088)
	Training done	0.297 (0.078)	0.349 (0.082)	0.397 (0.084)
Number of overbids	Prices posted	0.153 (0.047)	0.216 (0.046)	0.207 (0.041)
	Training done	0.270 (0.044)	0.279 (0.046)	0.293 (0.053)

---

Appendix A: Unique bids and number of overbids

---

Table A1. Unique bids and number of overbids.

	Number of overbids
Unique bids	0	1	2	3	Total
1	33	1	2	1	37
2	52	8	0	0	60
3	98	8	0	1	107
4	176	9	6	2	193
5	147	12	6	12	177
6	103	11	5	17	136
Total	609	49	19	33	710

---

Appendix B: Conditional analysis

To gain further insights, we also estimated random effects probit models¹² that included as covariates the dummies for the treatments, a variable indicating the round, gender, age, perceived economic position of the household, household size, total fee (to control for money endowment effects), a variable indicating comprehension of the payoff mechanism of a lottery, and a variable indicating competitiveness traits of the subject.¹³ The coding of the variables is exhibited in Table B1. Variables that are not indicated to be dummy variables are treated as continuous variables. Some descriptive statistics of the associated variables are exhibited in Table B1.¹⁴

---

Table B1. Variables and variable description

Variable	Description	Mean	Std. dev.
WinLovLotA	Dummy, 1=subject bid over the best outcome for lottery A, 0=otherwise	0.11	0.31
WinLovLotC	Dummy, 1=subject bid over the best outcome for lottery C, 0=otherwise	0.08	0.26
WinLovLotE	Dummy, 1=subject bid over the best outcome for lottery E, 0=otherwise	0.09	0.28
TreatPrice	Dummy, 1=subject participated in the posted market clearing price treatment, 0= subject participated in the no-posted market clearing price treatment	0.51	0.50
TreatTrain	Dummy, 1=subject participated in the extensive training treatment, 0= subject participated in the minimal training treatment	0.51	0.50
Gender	Dummy, 1=male, 0=female	0.38	0.49
TotFee	Total endowment fee for participation	16.76	0.81
EconPosition1*	Dummy, 1=economic position of the household is good or very good, 0=otherwise	0.34	0.47
EconPosition2	Dummy, 1=economic position of the household is above average, 0=otherwise	0.26	0.44
EconPosition3	Dummy, 1=economic position of the household is average or worse, 0=otherwise	0.40	0.49
Age	Subject’s age	20.74	1.54
Hsize	Household size	4.45	1.11
Comprehension	Score of comprehension of lottery’s payoff mechanism	2.75	1.07
Competitiveness	Subject’s competitiveness traits	21.05	4.28
* Removed from estimation

---

Table B2 exhibits semi-elasticities of the form of ∂ (ln (Prob (Y = 1 | X)) ) /∂ (X) which indicate the percentage change in the probability of the dependent variable Y resulting from a unit change in X¹⁵. We can see from Table B2¹⁶ that both comprehension and competitiveness have a statistically significant effect on the probability of bidding more than the best outcome of the lottery. Specifically, competitiveness positively affects the probability of being an overbidder while, comprehension of the lottery’s payoff negatively affects the probability of being an overbidder. The effect of comprehension is, however, statistically significant for only one lottery (lottery C). One could therefore conclude that the observed behavior in the lab of bidding more than the best outcome of a lottery can be explained more by competitiveness traits and less by comprehension of the payoff mechanism of the lotteries. The magnitude of the effects also reflects this conclusion. For example, subjects that differ in their competitiveness by 25% in the employed scale (corresponding to a 6-point increase in competitiveness; given that competitiveness ranges from 4 to 28) are 7.3% more likely to overbid for lottery C.¹⁷ The corresponding effect (a 25% increase) for comprehension results in only a 4.7% decrease in the probability of overbidding for lottery C.

---

Table B2. Estimated semi-elasticities from random effects probit models and pooled probit model (overbidders). (Standard errors in parentheses.)

	Lottery A	Lottery C	Lottery E	Pooled model
Round	0.409** (++) (0.119)	1.258** (++) (0.406)	0.833** (++) (0.319)	0.359** (++) (0.086)
TreatPrice	1.575 (1.321)	12.978* (++) (7.117)	5.605 (4.038)	2.323** (++) (0.879)
TreatTrain	1.68 (1.395)	10.961 (++) (6.932)	7.467 (+) (4.954)	2.007** (++) (0.885)
Gender	3.112** (++) (1.453)	5.042 (4.178)	1.082 (3.233)	1.608 (+) (0.998)
TotFee	−0.106 (0.827)	4.711 (+) (3.418)	−1.306 (2.337)	0.175 (0.462)
EconPosition2	4.432** (++) (2.038)	8.972 (+) (5.901)	2.674 (4.989)	2.816** (++) (1.102)
EconPosition3	1.275 (1.645)	0.271 (4.416)	7.338 (5.291)	1.466 (1.134)
Age	−0.312 (0.411)	−1.583 (1.321)	−3.538** (++) (1.771)	−0.576** (++) (0.286)
Hsize	0.024 (0.513)	0.609 (1.901)	0.642 (1.589)	0.067 (0.254)
Comprehension	−0.897 (0.632)	−4.730* (++) (2.746)	−1.467 (1.639)	−0.878** (++) (0.299)
Competition	0.458** (++) (0.222)	1.810* (++) (1.085)	1.225 (++) (0.769)	0.369** (++) (0.114)
Probability of win	−	−	−	8.049** (++) (2.168)
Max payoff	−	−	−	−0.246** (++) (0.118)
Min payoff	−	−	−	0.662 (0.491)
Number of observations (groups)	650 (65)	650 (65)	650 (65)	3900
*(**) Semi-elasticity is statistically significant at the 10%(5%) level.
+(++) Corresponding coefficient is statistically significant at the 10%(5%) level.

---

These results further indicate that the overbidding effect is more likely to occur as the rounds evolve. For lottery C, posting the market clearing price between rounds did have an effect on the probability of being an overbidder. It is possible that posting of price information for the lottery exacerbated competitiveness. Training has a positive effect as well (note that the corresponding coefficients are statistically significant while the semi-elasticities are not; see footnote 15) which indicates that misconceptions about the elicitation mechanism is not the primary cause for the effect we observe. On the contrary, resolving any misconceptions resulted in higher bidding which made the overbidding effect more likely. As for the demographics, results suggest that males and younger subjects are more likely to be classified as overbidders than females and older subjects, respectively.

To further explore the issue of why subjects exhibited overbidding behavior only in specific lotteries, we estimated pooled probit regressions (last column in Table B2) where we used lottery characteristics (i.e., the probability of winning the lottery, the maximum payoff of the lottery and the minimum payoff of the lottery) as independent variables. Table B2 shows that the overbidding effect attenuates when we move to lotteries with high maximum payoffs, which explains why we did not observe such an effect for lotteries B and D. In addition, the probability of winning is positively associated with the probability of overbidding in any given lottery. It appears that moving from uncertain to certain outcomes (i.e., increasing the probability of winning) reduces the costs of misbehaving with respect to optimality.

To test whether the overbidding effect is associated with subjects deriving utility from being winners in previous round auctions we also estimated a specification where we included a dummy variable indicating whether the subject had won a previous round auction and a variable indicating the cumulative number of auctions the subject had won up to a round. Results provide further evidence that winning in any single previous round is not enough to cause the overbidding effect. However, the cumulative number of auctions won, positively affects the probability of overbidding. Results are provided in Table B3.¹⁸

---

Table B3. Estimated semi-elasticities from random effects probit models and pooled probit model (overbidders).

	Lottery A	Lottery C	Lottery E	Pooled model
Round	0.240 (+) (0.154)	0.698** (++) (0.355)	−0.008 (0.272)	0.424** (++) (0.101)
TreatPrice	2.491* (++) (1.353)	9.931* (++) (5.429)	5.375* (++) (3.090)	4.646** (++) (0.759)
TreatTrain	2.341 (++) (1.450)	8.437 (++) (5.208)	6.429* (++) (3.720)	3.543** (++) (0.704)
Gender	2.057 (+) (1.338)	3.132 (3.121)	−0.222 (2.340)	0.669 (0.506)
TotFee	−0.382 (0.762)	2.955 (2.558)	−1.690 (1.713)	−1.160** (++) (0.383)
EconPosition2	4.149** (++) (1.885)	6.676 (+) (4.398)	2.451 (3.671)	4.206** (++) (0.784)
EconPosition3	1.769 (1.537)	0.174 (3.237)	5.435 (+) (3.670)	1.917** (++) (0.656)
Age	−0.300 (0.365)	−1.039 (0.984)	−2.394* (++) (1.270)	−0.417** (++) (0.169)
Hsize	−0.232 (0.513)	0.285 (1.398)	0.433 (1.156)	−0.315 (0.233)
Comprehension	−0.760 (0.573)	−3.257 (++) (2.051)	−0.624 (1.214)	−0.653** (++) (0.253)
Competition	0.579** (++) (0.279)	1.294 (++) (0.803)	0.877 (+) (0.554)	0.436** (++) (0.097)
Previous round winner	1.087 (0.830)	0.848 (1.608)	−0.137 (1.513)	7.794** (++) (0.936)
Cumulative number of wins	0.898** (++) (0.390)	0.869 (0.764)	1.898** (++) (0.794)	1.352** (++) (0.222)
Probability of win	−	−	−	14.178** (++) (2.663)
Max payoff	−	−	−	−0.534** (++) (0.183)
Min payoff	−	−	−	0.885 (4.569)
Number of observations (groups)	585 (65)	585 (65)	585 (65)	3900
*(**) Semi-elasticity is statistically significant at the 10%(5%) level.
+ (++) Corresponding coefficient is statistically significant at the 10%(5%) level.

---

Table B4. Estimated semi-elasticities from random effects probit models and pooled probit model (overbidders). (Standard errors in parentheses.)

---

	Pooled model for lotteries A, C and E	Pooled model
Round	0.246** (++) (0.056)	0.251** (++) (0.053)
TreatPrice	1.652** (++) (0.602)	1.624** (++) (0.577)
TreatTrain	1.538** (++) (0.608)	1.475** (++) (0.608)
Gender	1.090 (0.720)	1.164* (+) (0.708)
TotFee	0.147 (0.329)	0.123 (0.327)
EconPosition2	2.002** (++) (0.783)	1.991** (++) (0.743)
EconPosition3	1.044 (0.799)	1.034 (0.793)
Age	−0.431** (++) (0.196)	−0.383** (++) (0.193)
Hsize	0.072 (0.180)	0.052 (0.178)
Comprehension	−0.659** (++) (0.207)	−0.615** (++) (0.194)
Competition	0.270** (++) (0.084)	0.261** (++) (0.079)
Probability of win	4.393 (8.518)	−
Max payoff	0.012 (0.721)	−
Lottery E	−	−1.011** (++) (0.414)
Lottery F	−	−2.871** (++) (0.843)
Lottery C	−	−1.263** (++) (0.299)
Number of observations	1950	3900
*(**) Semi-elasticity is statistically significant at the 10%(5%) level.
+(++) Corresponding coefficient is statistically significant at the 10%(5%) level. Notes: First column displays estimated semi-elasticities using only the sub-sample of lotteries A, C and E (the P-bet lotteries). Minimum payoff does not vary for these lotteries and was excluded from the covariate list. A model for lotteries B, D and F cannot be estimated due to low variability of the dependent variable. Second column of results displays estimated semi-elasticities using lottery dummies instead of lottery characteristics. Observations for lotteries B and D were dropped due to no variability of the dependent variable. Lottery A is the base category.

---

Appendix C: Experimental instructions

*

Department of Economics, University of Ioannina, University campus, 45110, Ioannina, Greece. Email: adrihout@cc.uoi.gr.

#

Department of Agricultural Economics & Agribusiness, University of Arkansas, USA. Email: rnayga@uark.edu.

%

Department of Agricultural Economics, Oklahoma State University, USA. Email: jayson.lusk@okstate.edu.

§

Department of Agricultural Economics & Rural Development, Agricultural University of Athens, Greece. Email: t.lazaridis@aua.gr.

1

We emphasize that it is not our objective in this study to replicate the uncertainty effect by any means. In fact, since we did not allow negative values in the lottery auction task in order to ensure that subjects do not bid negative values out of strategic reasons, we excluded the uncertainty effect by design. However, the effect we observe in the experiment is analogous to the opposite of the uncertainty effect and the discussion of the Gneezy, List and Wu (2006) study helps us place our finding in this context. While theories that explain the uncertainty effect have appeared in the literature, there is no coherent theory of preferences that can explain why someone would bid more than the maximum value of the lottery in our study. In this respect, our finding challenges the expected utility theory as well as prospect theory.

2

In the experimental auctions literature, overbidding is defined as bidding more than an assigned (induced) value (e.g., Cooper & Fang, 2008, Delgado, et al., 2008, Dorsey & Razzolini, 2003, Kagel, et al., 1987). In our paper we did not assign induced values; we instead elicited private (homegrown) values for the lotteries. Normally, we would expect subjects’ private value to lie somewhere between zero and the maximum payoff of the lottery. Bidding higher or lower than the expected payoff of the lottery could be reasonably explained by “risk loving” or “risk averse” preferences. In fact, since we did not induce values, the term overbidding in the sense used in the induced value auction literature, is not relevant to our study. Hence, in this study, we define overbidding as the extreme bidding we observe when subjects bid more than what a specific lottery can potentially payoff. We find this interesting in its own rights since it violates expected utility and prospect theories.

3

In every step that involved random drawings by the computer, we reassured subjects that the drawing was fair and that extra care was taken by the programmer to make sure that this is the case.

4

The products we used were a packet of gums, a bag of cookies and a bag of potato chips.

5

The training procedure that we adopted for the full training treatment is similar to the training procedure used by Plott and Zeiler (2005) to show that clearing out subjects’ misconceptions about the auction mechanism can turn off the endowment effect. In addition, in a paper where we analyze relative valuations from this experiment (Corrigan et al., 2012) we found that training can make a difference. We therefore believe that this type of training was effective in enhancing understanding or clearing out misconceptions.

6

We had to modify the chances into a percentage form since in the original paper these were given in a different format. The expected payoffs are very close to the ones reported in the original paper.

7

The P-bet lottery involves a bet with a high probability of winning a modest amount and a low probability of losing an even more modest amount and the $-bet involves a bet with a modest probability of winning a large amount and a high probability of winning a modest amount.

8

The data from the choice and the auction task are used to infer consistency of relative valuations in Corrigan et al. (2012).

9

The simultaneous appearance of lotteries may have triggered a carry-over effect i.e., carrying over one bid from one lottery to another. If this is true then the fact that one subject overbids in one lottery, makes it more likely to overbid in another lottery. To rule out this effect we examined the number of unique bids made by each subject by creating a variable assigned the value equal to the number of unique bids submitted by the subject (a subject who made the same bid every time gets 1; a subject who made a different bid for each lottery gets 6). The correlation of this measure with the number of overbids (number of lotteries that subject bids more than the maximum amount) is positive but low in magnitude (0.181). In addition, Table A1 in the appendix, indicates that overbids were most common among those who had a uniqueness score of 6, which means that the same bid is never carried over from lottery to lottery and that overbids are not the result of carry-over effects. We thank the editor for pointing this out to us.

10

Although the number of cases for lottery F was very small (2 cases).

11

Table 2 gives us an indication that overbidding is more prevalent for P-bets with high maximum payoffs than P-bets with low maximum payoffs. This does not explain why subjects bid more than the maximum payoff of the lottery. In theory, the auction mechanism we employ gives the incentive to bid one’s true value for the lottery. However, that private value should lie somewhere between zero and the maximum payoff of the lottery. The 2^nd price auction also poses some cost on misbehaving i.e., not bidding one’s true value for the lottery: the subject may have to pay more to buy the lottery in question than what s/he intended to. Obviously, for lotteries with high amounts of winning (lotteries B, D, F) subjects who overbid run the risk of losing more money if the positive outcome of the lottery is not realized. We show later in the paper that this overbidding behavior is mainly driven by competitiveness traits. Hence, it is an indication that subjects may be willing to experience the joy of competitiveness or winning when the possible cost of this behavior is low but not when it is high (given that in lotteries with small maximum amounts, subjects have higher probabilities of getting the positive outcome).

12

A probit model is a regression type approach appropriate when there is a binary outcome, as in our case. The probit model basically transforms the binary outcome into probabilities using the cumulative distribution function of the normal distribution. In addition, since the same units (subjects) were repeatedly sampled (multiple rounds in the auction; equivalent to a time dimension) at each level of the independent variables, our data have a panel structure. Using random effects at the individual level allows us to estimate trends in the binary outcome. See Gibbons and Hedeker (1994) for more details.

13

To account for the fact that bids may not be independent within a group of any given session we also added random effects for the group in the model. However, likelihood ratio tests showed that this model did not fit the data significantly better than the model without random effects for group. This may be an indication that the groups did not differ much in the “atmosphere of competition” that might have evolved during the auctions.

14

Since in the telephone interviews we were unable to establish contact with 6 subjects, subsequent tables refer to a sample size of 65 subjects out of the 71 that participated in the experimental auctions.

15

Table B2 shows the statistically significant semi-elasticities as well as the variables with statistically significant coefficients. We estimate semi-elasticities because the coefficients from a probit model are not quantitatively interpretable as in an OLS regressions. Therefore, coefficients are not displayed given that these are quantitatively meaningless. Semi-elasticities from a probit model are of the form ∂ ( ln( Prob( Y=1|X ) ) )/∂ X where Prob=Φ ( b^′X ) and Φ is the cumulative distribution function of the normal distribution. In OLS regression, tests of the significance of a predictor are based on t-tests of the coefficients. Similarly, in a probit model we can test for the significance of a variable by testing whether the coefficient is significantly different from zero. However, it might also be of interest whether an estimated semi-elasticity is significantly different from zero. The later is a test of whether a non-linear function of all the coefficients in the model is significantly different from zero and is not equivalent to a test of whether the coefficient is zero. Thus, Table B2 exhibits results from both tests.

16

We could not estimate a random effects probit model for lottery F due to small variability in the dependent variable.

17

This corresponds to multiplying the semi-elasticity by a factor of six.

18

We also estimated a pooled regression for lotteries A, C and E (the P-bets) separately and a pooled regression using lottery dummies instead of the probabilities and amounts of winning. A regression for lotteries B, D and F (the $-bets) cannot be estimated due to low variability of the dependent variable. Results are depicted in table B4 in the Appendix. It is evident that estimated effects (especially for the variables of interest, Comprehension and Competition) are robust across alternative models and specifications. We thank an anonymous reviewer for suggesting this.

This document was translated from L^AT_EX by H^EV^EA.