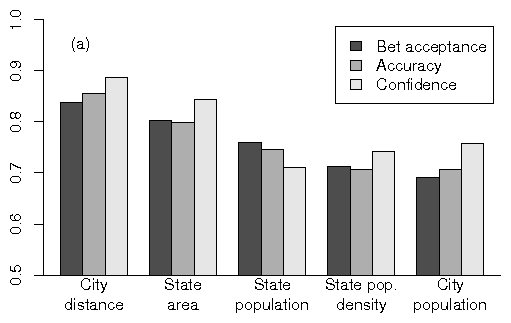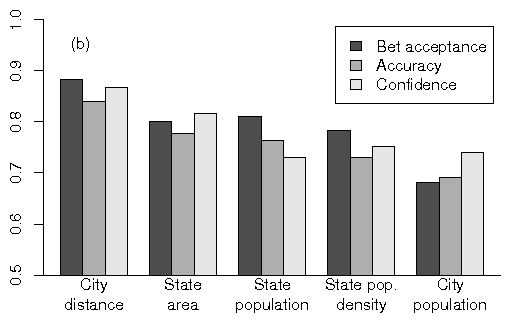The skill element in decision making under uncertainty: Control or competence?

Adam S. Goodie1   and Diana L. Young
University of Georgia

Judgment and Decision Making, vol. 2, no. 3, June 2007, pp. 189-203,

Abstract

Many natural decisions contain an element of skill. Modern conceptions of the skill component include control (Goodie, 2003) and competence (Heath & Tversky, 1991). The control hypothesis states that a task's skill component (the sensitivity of the task to skill) affects decision making; the competence hypothesis states decision making is affected only if the participant possesses the skill. Three experiments compared risk taking patterns between two groups. One group faced bets on random events, and another group faced bets on their answers to general knowledge questions, which is a task characterized by control. In Experiment 1, control increased risk taking markedly with all statistical properties held constant. In Experiment 2, decisions made in domains of varying difficulty, and by individuals of varying ability, yielded further qualified support for the role of competence. In Experiment 3, the role of control was replicated, and participants' perceptions of the differences in group treatments aligned more with the implications of the control hypothesis than with the competence hypothesis. Results offered support for the control hypothesis across a range of competence.

Keywords: control, competence, decision making, choice, betting, risk, overconfidence, college students.


1  Introduction

Decision researchers know a great deal about the terms of risk that people will accept and reject on random events such as the drawing of a lottery number, rolling a die, or pulling a poker chip from a bookbag. Less is known about how individuals accept or reject risk when they are betting on their own golf putts, stock picks, organizational decisions or answers to trivia questions.
Researchers readily build models of decision making around risky decisions based on random events. Much decision research is analogous to psychophysical perception research, relating psychological events to objective criteria. A bookbag with 70 percent white and 30 percent red poker chips presents a clear objective criterion to which subjective perceptions may readily be compared. Sinking a free throw does not present such a clear criterion with regard to its associated probabilities. For this reason, researchers have difficulty in evaluating performance relative to a normative criterion when the task is assessing the probability of a made free throw, as well as in establishing valid lawful relationships between relevant probabilities and decisions.

1.1  Ambiguity and skill

Ellsberg (1961) and many others have found that people are generally ambiguity averse; in the domain of gains, people prefer a prospect in which probabilities of possible outcomes are known to a prospect in which probabilities of the same outcomes are not stated (ambiguous) but have the same average value. The major exception to this is at very low probabilities, where ambiguity is preferred. In the domain of losses, these preferences are reversed.
Examination of the effect of a skill element constitutes a special case of ambiguity. What is Shaquille O'Neal's probability of making his next free throw? At the conclusion of the 2006-07 season, his career free throw rate was 52.5%, but his free throw rate for the season was only 42.2%. At his next free throw opportunity, he may be suffering from the flu, or coming off a terrible game, or on a hot streak, or he may merely believe he's on a hot streak (Gilovich, Vallone, & Tversky, 1985). Unlike a lottery draw, in which it is easier to construct a reasonable estimate of the probability of winning (for example, by reading the ticket), the sample space for a successful free throw is not clearly defined. In other words, the prediction of performance is variable over time in a skilled task, hence it is more difficult to predict on the basis of past performance. In fact, most definitions of skill state or imply that the person exerting skill can change the probability of success.
The existing evidence suggests that a skilled task that determines an uncertain outcome has an effect on probability assessment and decision making that is distinct from that of ambiguity alone. For example, in demonstrating the illusion of control, Langer (1975) showed that people responded differently to vague likelihoods when certain superficial characteristics of the prospects were distorted, for example when the familiar symbols of a deck of cards were replaced by unfamiliar symbols, or when participants were permitted to practice on a random mechanism similar to a roulette wheel. Langer argued that the changes in the appearance of a skill component caused changes in responses. Confidence ratings, bet acceptance and bet amounts were all affected by apparent control, although the illusion of control is not robust to multi-shot gambles (Koehler, Gibbs, & Hogarth, 1994). Participants bet more when given skill-relevant manipulations such as being able to choose whether to receive more cards in a simulated blackjack game, but not when given skill-irrelevant manipulations such as choosing a different dealer (Chau & Phillips, 1995). Also, participants high in desire for control bet more than those low in desire for control on events over which they had falsely perceived control. Those high in desire for control bet less than others on events over which they did not have illusory control (Burger & Schnerring, 1982).

1.2  Control and competence


Recent research has advanced two major conceptions of the role of skill in decision making: competence (Heath & Tversky, 1991) and control (Goodie, 2003). These conceptions have important commonalities, sharing an emphasis on the role that the skill component of a task plays in shaping decision making under uncertainty (apart from the probability and magnitude of possible outcomes. The control hypothesis claims that people bet more when skill makes a difference; the competence hypothesis claims the same effect but only when an individual possesses the relevant skill. Control is a property of the task: if the task requires actions that can be learned, then it is characterized by control, even if a participant has not yet learned the skill. Competence, on the other hand, is an interactive characteristic of both the task and the person: competence exists only if the task both can be learned (the task component) and has been learned (the person component).
Heath and Tversky (1991) argued that people prefer to bet on questions about knowledge topics in which they feel competent rather than incompetent. In their studies, participants chose to bet on either the correctness of their answer to a general knowledge question or a random event whose probability matched their previously stated confidence, with identical payoffs in each bet offer. Across an assortment of situations, when betting on questions drawn from intermixed domains, the proportion of times that participants chose to bet on their knowledge was a steeply increasing function of the probability of winning (Experiments 1 and 3). Because confidence consistently exceeded accuracy in these experiments, betting on a random event whose probability of winning was equal to confidence was more likely to win than betting on the belief itself, and Heath and Tversky (1991) noted that the acceptance of knowledge-based bets over random bets resulted in a 15% loss of expected earnings.
Heath and Tversky then (Experiment 4) tested the competence hypothesis by drawing questions from discrete domains in which participants believed themselves to be either competent or incompetent. They observed that, with subjective probability held constant, participants displayed a consistent behavioral pattern: bets in a domain of competence were preferred to bets on random events, which in turn were preferred to bets in a domain of incompetence. They concluded that people seek out ambiguity in domains of competence but avoid it in areas of incompetence.
Fox and Tversky (1995; Fox & Weber, 2002; see also Chow & Sarin, 2001) presented a companion to the competence hypothesis, the comparative ignorance hypothesis, positing that relative knowledge affects decisions most strongly when the contrast between conditions of greater and lesser competence is brought to the decision maker's attention.
These findings are notably contrary to the early ambiguity findings with random events: when evaluating bets on vaguely probable events with a skill component, participants preferred the ambiguous (skilled) option at high probabilities but preferred the unambiguous (random) option at low probabilities. However, the evidence specifically in support of the control hypothesis remains limited to Heath and Tversky's Experiment 4 comparing just two domains under unusual selection techniques, which are discussed at more length below.
More recent studies (Goodie, 2003) assessed risk attitude by pitting a bet on knowledge item against no bet at all, rather than a bet on a random event of equivalent probability. Goodie constructed bets on knowledge items to be fair, having zero average marginal value if confidence was well calibrated. In the first two experiments, bet acceptance sharply increased as confidence increased for knowledge bets, bearing a striking resemblance to the comparable data obtained by Heath and Tversky (1991) when using mixed-domain questions. In Experiment 3, one group considered bets on their knowledge. The other groups considered bets on events that appeared random to participants but that Goodie constructed to be identical in every statistical way to bets on knowledge. Participants accepted more bets on random events at low probabilities and more bets on their knowledge at high probabilities, revealing the anticipated crossover effect.
An important difference arises between studies that utilize questions drawn from a single domain (e.g., U.S. history) and those that use questions from mixed domains (e.g., Greek mythology, U.S. history, and sports). As Heath and Tversky (1991) noted in discussing the differences between single and mixed domains, low confidence items in mixed-domain populations will systematically include more questions from low-competence domains. Similarly, Gigerenzer (1991) noted the importance of utilizing single-domain questions in assessing confidence in answers. In a mixed-domain set of general knowledge questions, the methods used by the decision maker to generate confidence assessments become uninterpretable because the decision maker may be using a different reference set than the experimenter. Asking participants questions in a single domain allows for more reliable representations of confidence across all questions asked.
There is reason to expect that control per se influences decision making. Skinner (1996), in a major review of the literature, notes that "[w]hen people perceive that they have a high degree of control, they exert effort, try hard, initiate action, and persist in the face of failures and setbacks; they evince interest, optimism, sustained attention, problem solving, and an action orientation" (p. 556, cf. Seligman, 1975). Where control prevails, a prospect with negative expected value, narrowly conceived, might also be an opportunity to learn new skill that will result in future prospects with positive value, and might therefore be worth accepting. This is an interesting complement to the normative argument made by Frisch and Baron (1988; Baron, 2000) that other ambiguous prospects, even with positive expected value, might be worth postponing until further information is available to permit better-valued decisions. We argue that ambiguous prospects characterized by control, even with negative expected value, might be worth pursuing in order to set up better-valued decisions later. The possibility of accepting bets in order to increase skill does not apply when competence already exists, only when the possibility of exerting control to increase competence prevails.

1.3  The present experiments

The goals of this paper are: a) to compare across domains wherein people have different degrees of competence, in order to observe the degree to which variation in competence makes a difference in risk attitude; b) to extend the risk-attitude findings of Goodie (2003) to single-domain formats, a manipulation that made a considerable difference in the ambiguity-attitude findings of Heath and Tversky (1991); and c) to begin to compare the roles of competence and control in decisions under uncertainty. The present experiments test the competence hypothesis against the control hypothesis by eliciting betting decisions within domains of varying difficulty and among participants of varying ability.
The distinction between competence and control is most evident in a skill-based task in which a particular participant has little skill. The control hypothesis suggests people bet more when skill could be attained, the competence hypothesis only when it has been attained. We can best differentiate between these two hypotheses when skill could be attained but has not. The control hypothesis suggests the skill element does alter decision making under such conditions, whereas the competence hypothesis suggests it does not.

1.4  General Method

We report three experiments which use the methods developed by Goodie (2003; Campbell, Goodie, & Foster, 2004). The basic task of fair bets on knowledge uses three kinds of questions, administered in two phases.

1.4.1  Phase 1. General knowledge and confidence assessment

The first question type was a two-alternative forced choice question. Prior studies (Goodie, 2003) adapted questions from a collection (Nelson & Narens, 1980) that sampled from diverse domains. The present studies randomly selected questions from five well-defined domains. Three question populations selected two of the 50 U.S. states at random and asked for a binary comparison on one statistic: population, land area, or population density, manipulated between-subjects. The other two question populations randomly selected two of the 50 largest U.S. cities and elicited a comparison of the cities on either population or driving distance to Athens, Georgia.2
The second question type asked for an assessment of confidence in each question, placed in one of the following categories: 50-52%, 53-60%, 61-70%, 71-80%, 81-90%, 91-97%, and 98-100%. In a binary task such as this one, the range of 50%-100% reflects the full range of competence, from complete ignorance where accuracy would be 50% and confidence should not be much higher, to absolute knowledge where accuracy and confidence are both 100%. Confidence was taken as the midpoint of the selected confidence category. We used these categories to assess risk taking across a well-defined array of probabilities from chance to certainty, combining equal spacing of categories in the mid-range and greater discrimination near the endpoints. This range confers the advantages of reflecting all binary choices and being simple and easily understood, although it also bears the clear limitations of excluding half the probability spectrum. These studies adopted confidence elicitation methods without alteration from those used by Goodie (2003; Campbell et al., 2004).

1.4.2  Phase 2. Betting on answers

A third question type elicited acceptance or rejection of a bet on the correctness of each answer that was given. Participants played out these bets for point accumulations that were not backed by monetary incentives. In all conditions, participants faced a two-alternative choice between a certain outcome and a bet. The bet was always fair, having average value equal to the certain option if the participant's confidence judgment was well-calibrated. Its average value was less than that of the certain option if the participant was overconfident and greater than the certain option if the participant was underconfident. After accepting or rejecting the bet, the participant received feedback, including the correct answer to the question, the number of points gained or lost (including if no points were gained or lost), and the cumulative point total.

1.4.3  The betting formats

We used two betting formats, with Mixed gains and losses, and Gains Only. The Mixed format was used in order to reflect the structure of many risks which contain the possibility of either gain or loss. The Gains Only format was used to eliminate the complexity of possibly differing value and weighting for gains and losses. We designed both betting formats to provide average outcomes that were equal if the bet was accepted or rejected, assuming good calibration. Betting formats were always varied between subjects, or were kept constant within an experiment, so that no participant needed to comprehend, remember, or distinguish between both.
In the Mixed format, the certain option was no change in points, and the bet provided for a gain of 100 points if the answer was correct or a loss of 100 * confidence/(1-confidence) points if the answer was incorrect. For example, if a participant was 75% confident in an answer, then she considered a bet wherein she won 100 points if the answer was correct but a loss of 100 * (.75/.25) = 300 points if the answer was wrong. If she rejected the bet, she did not gain or lose any points.
In the Gains Only structure, the certain option was a gain of 100 points. The bet offered a gain of 100 /confidence points if the answer was correct and no gain if the answer was wrong. So, if the participant bet on an answer in which she had 75% confidence, she won 100/.75 = 133 points if the answer was correct but nothing if the answer was wrong. She gained 100 points if she rejected the bet. It is easy to show that the average outcome of accepting a bet in either format is equal to the certain option (no change in the Mixed format or a gain of 100 points in Gains Only) if p(correct) = confidence, less than the certain option if p(correct) confidence, and greater than the certain option if p(correct) confidence.
Table 1: Structure of the experiments
N Question Types Betting Format Survey
1 single domains mixed and gains-only No
1a 76 state population mixed No
1b 67 city population mixed No
1c 48 state population gains-only No
1d 35 city population gains-only No
2 single domains mixed and gains-only No
2a 112 5 groups* mixed No
2b 152 5 groups* gains-only No
3 185 state population gains-only Yes

1.4.4  "Answers" and "Random" groups

In Experiments 1 and 3, we randomly assigned participants to two groups that differed in whether they believed they were betting on their knowledge or on a random event. The Answers group bet on their answers, using either the Mixed or Gains Only format in different experiments. The Random group's bets held all statistical properties constant, differing from the Answers group's only in appearing to rely on random events rather than participants' answers. Many dimensions of bets on knowledge are determined by the participants' responses, such as the distribution of subjective probabilities of winning (determined by confidence), the frequency of winning (determined by accuracy), and any order effects on these dimensions (for example, if overconfidence declines with experience, cf. Sieck & Arkes, 2005, or accuracy declines with fatigue, or any number of other possibilities). By basing the apparently random bets on the participant's responses, we can rule out these and any other alternative explanations based on such statistical properties of the responses of participants in the Answers condition.
Bets that appeared stochastic in fact relied on participants' answers and confidence assessments in the knowledge questions. In the betting phase, each answer was converted into a bet on a seemingly random event with the stated probability of winning equal to assessed confidence in a corresponding trivia answer; the correctness of the corresponding answer determined the bet's outcome. For example, if a participant expressed 75% confidence in her answer to the first question, then the first bet she encountered in the betting phase instructed: A number will be chosen at random between 0 and 100, and to win the bet, the Chosen number must be less than or equal to the Magic Number. The Magic Number this time is: 75. If the chosen number is LESS THAN or equal to the Magic Number, you gain 100 points. If the chosen number is greater than the Magic Number, you lose 300 points. If the participant accepted the bet, she won the bet if her answer to the corresponding question was correct and lost the bet if her answer was incorrect. The Magic Number, the magnitude of the gain if the bet was won, and the determination of whether the bet was won or lost changed on each betting trial to reflect the confidence expressed in the corresponding answer from the first phase and whether it was correct.

1.4.5  Other general facets

In all experiments, we recruited participants from the Research Pool of the Psychology Department at the University of Georgia and compensated them with partial credit toward lower-division courses. We prevented participants from participating in more than one of the present experiments or in any additional related experiments. Participants ran in groups of up to three in a room with individual computer stations separated by five-foot-tall partitions. We omitted participants' data from analysis if they did not use more than three confidence categories, or if they showed evidence of not attending to the task (i.e., exclusive betting acceptance or rejection, or radical over- or underconfidence). Thirty participants were excluded for this reason (13 out of 239 in Experiment 1, 10 out of 274 in Experiment 2, and 7 out of 192 in Experiment 3). See Table 1 for a layout of the structure of our experimental design.

2  Experiment 1

The first experiment assessed the effect of a skill component using items from single domains, comparing participants betting on answers with those betting on random events. Four sub-experiments utilized different question populations and betting formats.

2.1  Method

In Experiment 1a (N=76; 37 in Answers and 39 in Random), participants answered binary choices comparing states' populations and faced bets constructed in the Mixed format. In Experiment 1b (N=67; 33 in Answers and 34 in Random), participants compared cities in population with bets in the Mixed format. In Experiment 1c (N=48; 23 in Answers and 25 in Random), participants compared states' populations with bets in the Gains Only format. In Experiment 1d (N= 35; 17 in Answers and 18 in Random), participants compared cities' populations with bets in the Gains Only format.

2.2  Results

2.2.1  Confidence, accuracy and calibration

Average confidence, accuracy and over/underconfidence are given in Table 2.

2.2.2  Bet acceptance

The principal finding of these experiments is that, using questions from single domains with all statistical properties of bets held constant between groups, participants consistently accepted more bets when betting on their answers than they did when betting on random events. These results are presented in Table 3 and show dramatically greater rates of bet acceptance in the Answers group in all four sub-experiments, which were statistically significant in all cases. Averaged across sub-experiments, those betting on their answers accepted 75.8% of all bets, and those betting on random events accepted 55.5% of all bets.
Table 2: Average confidence, accuracy and overconfidence in Experiment 1, and comparisons between Answers and Random groups.

Experiment Answers Random t df     p
1a .751 .753 0.07 74       .95
1b .768 .764 0.21 65       .83
1c .780 .726 2.31 46     .026
1d .778 .756 0.80 33       .43
1a .745 .757 0.73 74       .47
1b .713 .713 0.01 65       .99
1c .760 .751 0.50 46       .61
1d .665 .694 1.07 33       .29
1a .007 -.004       0.57 74       .57
1b .055 .051 0.19 65       .85
1c .020 -.025       1.52 46       .14
1d .113 .062 1.33 33     .051
Table 3: Overall percentage of bets accepted on answers and random events in Experiment 1.

Experiment Answers Random t df p
1a 73.9 55.2 4.17 74 .000
1b 73.8 62.1 2.41 65 .019
1c 80.2 55.0 4.90 46 .000
1d 75.2 49.8 2.67 33 .012
Average 75.8 55.5
Betting rates conditionalized on confidence are shown in Figure 1. We found higher betting rates when participants bet on their own knowledge, compared with bets that were identical in every statistical way but appeared to rely on random events, at all confidence levels in all sub-experiments. Because accuracy did not differ significantly between groups, neither group experienced a systematically greater proportion of won bets. In addition, because overconfidence did not differ significantly between groups, neither group benefited from a systematically more favorable outcome for betting. The comparison of the betting curves is thus an appropriate reflection of the different appearance of betting on knowledge versus betting on random events, rather than a reflection of differing probabilities or magnitude of possible outcomes. Had we found a trend of higher accuracy or overconfidence in either group, the higher bet acceptance among those betting on knowledge would have suggested a different explanation for the difference in bet acceptance other than the difference between groups.
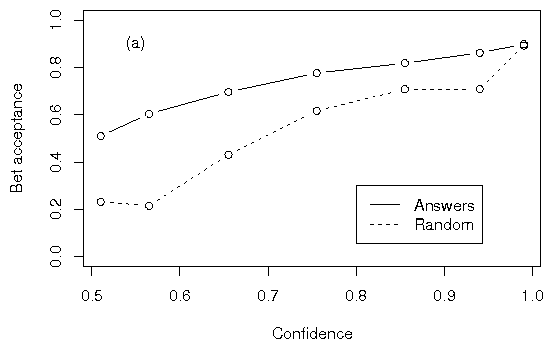
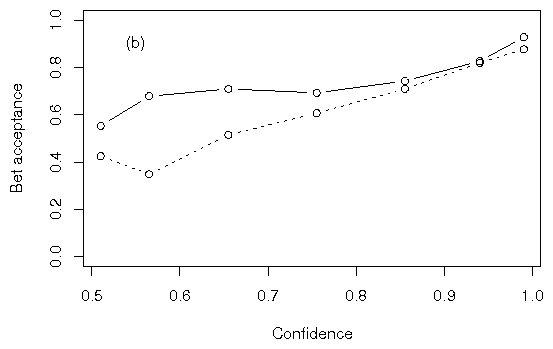
fig1a.pngfig1b.png
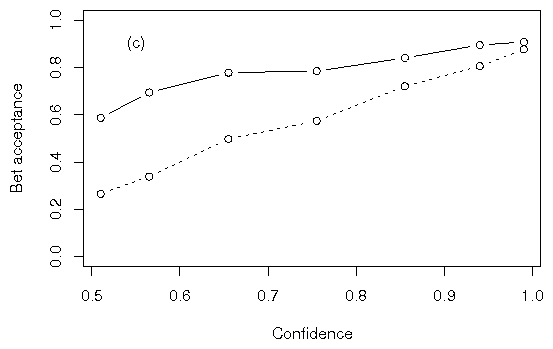
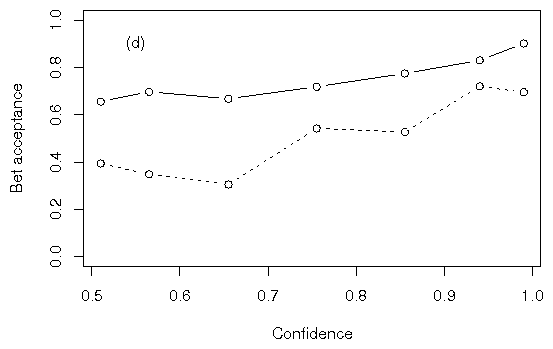fig1c.pngfig1d.png
Figure 1: Proportions of bets accepted in (a) Experiment 1a, (b) Experiment 1b, (c) Experiment 1c, and (d) Experiment 1d. Mean bet acceptance was aggregated across all subjects at each level of confidence, ignoring subject identity. At all confidence levels in all sub-experiments, participants accepted bets more frequently on answers than on random events.
The findings in bet acceptance mark a departure from what Goodie (2003, Experiment 3) observed with items from assorted domains, where participants bet on their knowledge relatively seldom at low levels of confidence and increasingly often as confidence increased. In the present experiments, rates of bet acceptance are higher for bets on answers at all levels of confidence, though there is still an increasing rate of bet acceptance as confidence increases, as can be seen in Figure 1. The comparison between the present experiments with single domains and past experiments with mixed domains resembles the trend across experiments in Heath and Tversky (1991). When Heath and Tversky narrowed the focus of questions, they observed a preference to bet on items in domains in which participants had competence that did not depend on probability level. That is, if a participant was competent in the domain of politics but felt uncertain about a particular political question, she still preferred to bet on that answer rather than an equally uncertain random event or item from a domain of incompetence. The current study incorporates the same narrowing of focus to a single domain, relative to the studies of Goodie (2003), and the same trend is observed: the increased risk preference does not depend on probability level.
Table 4: Descriptive statistics of confidence, accuracy, overconfidence and betting slope within the groups in Experiment 2.

Accuracy        Confidence Overconfidence
Experiment 2a        
City driving distance .856        .887 .030
State area .799        .843 .044
State population .746        .711 -.035      
State population density .707        .742 .035
City population .706        .758 .053
Experiment 2b        
City driving distance .840        .868 .028
State area .778        .817 .039
State population density .764        .730 -.033      
State population .730        .751 .021
City population .691        .741 .049

2.3  Discussion

These results indicate that control affects risk attitude when extended to the important case of a single domain, broadly across question populations. This supports the conclusion of Goodie (2003) that control affects risk attitude, but these findings suggest that the nature of that effect may be different within single domains than in mixed domains. Whereas in mixed domains participants showed betting proportions that were lower at low judged probabilities and higher at high judged probabilities (when compared to participants who bet on random events), participants who bet on their answers in this experiment accepted risk more often at all levels of confidence than those who bet on random events.
Goodie (2003) discussed the possibility of modeling the effect of control in terms of the probability weighting function proposed by Gonzalez and Wu (1999). This weighting function includes two parameters that are notable for their psychological plausibility: elevation, which reflects the overall attractiveness of risk; and curvature, which reflects the discriminability of different levels of probability. Goodie (2003), interpreting the betting proportions that increased with judged probability, speculated that the data could be accounted for by positing a more linear weighting function under conditions of control. The present data suggest that, when answering questions from well-defined domains with random sampling and transparent rules (i.e., under representative sampling), control may increase the attractiveness of risk and the elevation of the probability weighting function. However, these data do not permit firm conclusions on the mathematical form of the weighting function.

3  Experiment 2

In Experiment 1, the primary aim was to manipulate control to determine its effect on risky decisions in single domains. In Experiment 2, in order to test the competence hypothesis, we sought to observe differences in competence through both correlation and experimental manipulation and measure the effect of these competence differences on performance measures. One way to obtain diverse degrees of competence is to rely on naturally occurring variability in competence among participants, observing performance differences that depend correlationally on demonstrated knowledge in the content area. Another way is to observe differences that arise between groups when groups are given questions that differ in difficulty. We accomplished this by using five question populations: comparisons between pairs of U.S. states on population, land area and population density; and between pairs from among the fifty largest U.S. metropolitan areas on population and driving distance from Athens, Georgia. We assumed that some of these question populations would be more difficult than others and could be identified by showing a sizable degree of variability in average accuracy between groups. We also assumed that some participants would be more competent in each content area than others, which could be identified by differences in accuracy. Would people display different patterns of betting on a task characterized by control when they have different degrees of competence?3 If so, the competence hypothesis would be supported.
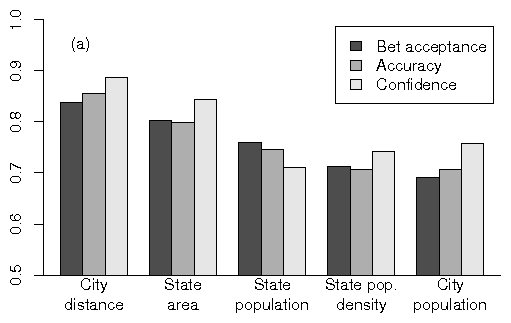
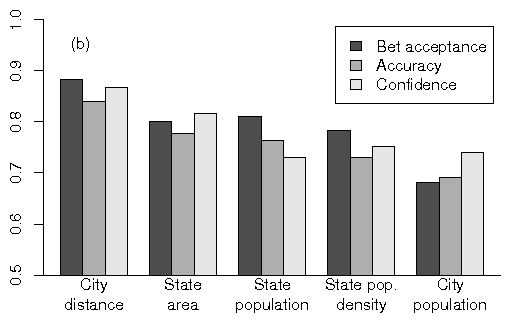fig2a.pngfig2b.png
Figure 2: Overall bet acceptance, accuracy and confidence in the five groups in (a) Experiment 2a and (b) Experiment 2b. Bet acceptance correlated strongly with accuracy, but this could be partly attributable to correlations between accuracy and confidence.

3.1  Method

Experiment 2a used the Mixed betting format; Experiment 2b used the Gains Only betting structure. We randomly divided participants (N=112 for Experiment 2a, 152 for Experiment 2b) into five groups, with each group differing in the domain of questions asked. Three groups answered questions seeking comparisons between pairs of randomly selected U.S. states on the dimensions of population (n=25 for Experiment 2a, 32 for Experiment 2b), land area (n=25 for Experiment 2a, 32 for Experiment 2b) and population density (n=25 for Experiment 2a, 32 for Experiment 2b). The other two groups made binary comparisons between U.S. cities on the dimension of metropolitan area population (n=18 for Experiment 2a, 28 for Experiment 2b) and driving distance from Athens, Georgia (n=19 for Experiment 2a, 28 for Experiment 2b).

3.2  Results

3.2.1  Confidence, accuracy and calibration

Confidence, accuracy and overconfidence values for the two sub-experiments are given in Table 4. Unlike in Experiment 1, differences in accuracy and confidence were not only expected but essential as a manipulation check for the effect of differential competence on betting.
Average accuracy at the group level ranged from .706 to .856 in Experiment 2a, and from .691 to .840 in Experiment 2b (Table 4). In a binary choice task, where the proportions are constrained to [0.5,1.0], this overall accuracy range of .165 is considerable. The differences among the groups defined by question domains were also statistically significant. In Experiment 2a, for accuracy, F (4,171)=22.2, p.001; for confidence, F (4,171)=22.6, p.001. In Experiment 2b, for accuracy, F(4,145)=18.9, p.001; for confidence, F(4,145)=15.0, p.001. The robustness of the differences in accuracy among the groups is reflected in a robust correlation of .864 between accuracy and confidence, using group averages in both sub-experiments as the unit of analysis.

3.2.2  Bet acceptance

Overall bet acceptance in the two sub-experiments is presented in Figure 2 as a function of groups, shown in descending order of accuracy among groups. Bet acceptance is closely correlated with accuracy at the group level - in Experiment 2a, r=.98; in Experiment 2b, r=.96 (each correlation based on five pairs). Such a correlation is the essential claim of the competence hypothesis; therefore, these very strong correlations constitute prima facie evidence for the competence hypothesis. However, one must remember that in such settings of betting on knowledge, betting frequency correlates positively with confidence, which is reflected in increasing betting curves such as those in Figure 1. Accuracy also correlates with confidence, as can also be seen in Figure 2 - in Experiment 2a, r=.88; in Experiment 2b, r=.84 at the group level. In short, when participants have competence, they also have high confidence, which may account for the increased bet acceptance. Consequently, as Heath and Tversky (1991) did in their Experiment 4, domains must be compared at equivalent levels of confidence.
We achieved this by comparing curves relating bet acceptance curves to confidence. Betting proportions across confidence categories for the five groups in both sub-experiments are shown in the two panels of Figure 3; each point on the graph represents the proportion of bets accepted at a given confidence level. The graph reflects increasing risk seeking as a function of subjective probability in all groups. Larger symbols reflect domains of greater accuracy. The competence hypothesis predicts larger symbols to appear above smaller symbols, and this prediction receives little support. It is clear that any differences between groups are small and do not reflect a consistent ordering as a function of competence.
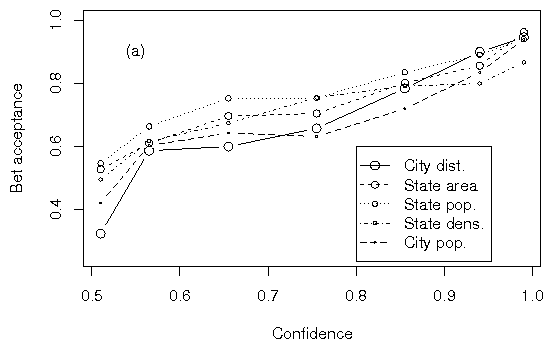
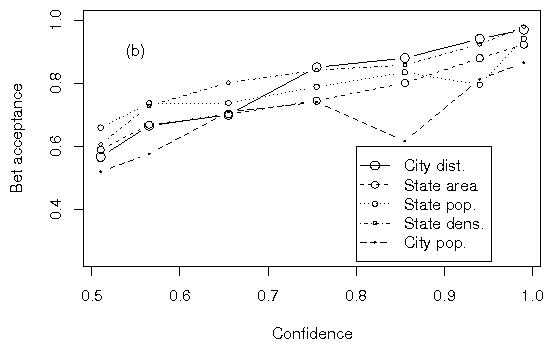fig3a.pngfig3b.png
Figure 3: Bet acceptance among the five groups in (a) Experiment 2a and (b) Experiment 2b. Groups with higher accuracy are depicted with larger symbols.

3.2.3  Individual variation

We also tested correlationally within groups for the effect of individual variation in competence on bet acceptance curves. For this analysis we constructed a linear model of each participant's betting function, using confidence level as the predictor variable and bet acceptance rate as the criterion. A linear model was used because the betting function has consistently been approximately linear at the group level in both Goodie (2003) and the present studies. This produced a slope and y-intercept for each participant. (Here, the y-axis reflects bet acceptance.) Then, in each sub-experiment, we computed a partial correlation between each individual's accuracy and the slope and intercept of their betting functions, controlling for the average accuracy observed in the participant's question domain group. We performed this partial correlation in order to observe only individual differences effects and not group treatment effects. In Experiment 2a, neither slope (r(170)=.089 ; p=.247) nor intercept (r(170)=-.038 ; p=.621) correlated significantly with accuracy. Given that slope was not significantly related to competence, the intercept was a reasonable measure of the overall attractiveness of risk. The absence of a significant correlation indicates that competence did not increase risk seeking. However, in Experiment 2b, as predicted by the competence hypothesis, accuracy did correlate positively and significantly with intercept (r(147)=.183, p.025), although the magnitude of the correlation is relatively small. (Slope and accuracy did not significantly correlate; r(147)=-.124, p=.133.)

3.3  Discussion

The results of these two sub-experiments provide further qualified support for the competence hypothesis. The correspondence between group-level accuracy and betting proportions is strikingly close, which, in addition to supporting the competence hypothesis, also bolsters the robustness of using binary choice tasks with a half-range probability spectrum. However, the correlations between accuracy and confidence, and between confidence and betting proportion, needed to be taken into account, and this diminished the strength of evidence in favor of the competence hypothesis. At the individual level, the partial correlation between accuracy and betting curve elevation was small but significant in Experiment 2b and non-significant in Experiment 2a.

4  Experiment 3

In Experiment 3, in addition to risk acceptance data, we sampled subjective measures of both competence and control. In this experiment, we replicated the methods of the earlier experiments but sought further to examine how participants' perceptions of their competence and control correlated with performance measures.

4.1  Method

Participants (N=185) all encountered state population comparisons, in the Gains Only betting format. They were divided into Answers (n=92) and Random (n=93) groups, which differed as they did in Experiment 1. In a third phase, all participants answered the following survey questions:
1. How competent do you feel you are at this task?
2. How do you think your abilities at this task compare to others?
3. How much control do you feel you had over this task?
4. If you were to do this task again one week from now, how much could you do between now and then to improve your performance?
Participants responded to these questions on a seven-point Likert scale labeled from 1 (not at all) to 7 (very much). The first two questions reflected responses to the term "competence" and to a definition of competence, respectively. The last two reflected responses to the term "control" and a definition of control utilized by Goodie (2003). The definition of competence conveyed in Question 2 reflects just one of multiple possible definitions. This definition is social in nature, comparing one's competence with that of others. For both Heath and Tversky (1991) and Fox and Tversky (1995), this is appropriate. We framed the survey question in a social-comparative way because non-comparative questions appeared to offer little more than synonyms of competence. The definition of control conveyed in Question 4 represented an attempt to reduce confusion about possible alternative definitions of the term control, such as internal control.

4.2  Results and Discussion

4.2.1  Calibration, overall bet acceptance and bet acceptance curves

Average confidence across both groups was .759, average accuracy was .751, and average overconfidence was .007. The difference between the two groups was less than .007, and statistically non-significant, for all three measures.
Once again, those betting on their own knowledge bet considerably more frequently than those betting on events that were identical in every statistical way but appeared random. The Answers group accepted 71.9% of all bets, whereas the Random group accepted only 45.6% of all bets. This difference was statistically significant (t(183)=7.77, p.001); thus, Study 3 replicated the large effect of control. Betting proportions across confidence categories for all three groups are shown in Figure 4 and reflect greater risk acceptance in all confidence categories when control prevails.
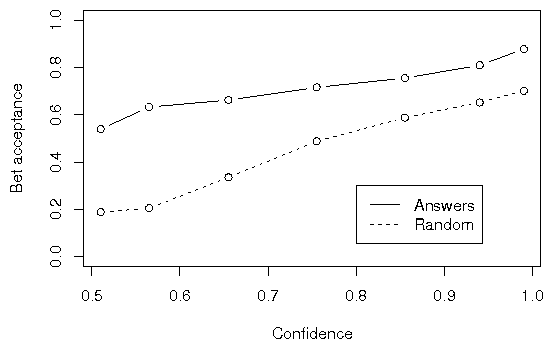fig4.png
Figure 4: Bet acceptance in the two groups in Experiment 3. As in Experiment 1, all calibration measures are equivalent, but the Answers group accepted significant more bets.

4.2.2  Survey results

Figure 5 depicts the survey results. On the seven-point scale that we used, there was a large difference between the groups in the perception of control as defined here (Question 4, t(183)=11.68, p.001). There was also a marginally significant effect on responding to the term "control" (Question 3, t(183)=1.78, p=.077). There was a small but statistically significant difference between the groups (t(182)=2.30; p=.023) in response to the term "competence" (Question 1) but in the opposite direction to that predicted by the competence hypothesis, with the Random group perceiving more competence than the Answers group. There was no difference between groups in perceptions of the social-comparative definition of competence (Question 2). It would appear from these survey data that, in the minds of our participants, the concept of control as defined here is prominent in explaining the effect of the control manipulation on risk taking. The term "control" itself, however, proved less compelling a description of the difference for our participants. Neither the term "competence" nor its social-comparative definition was able to account for how the groups perceived their conditions. This preliminary survey demonstrates that probability alterability appears to be pertinent to the perceived decision making processes of participants, but the terms "control" and "competence" may not be what they are thinking about.
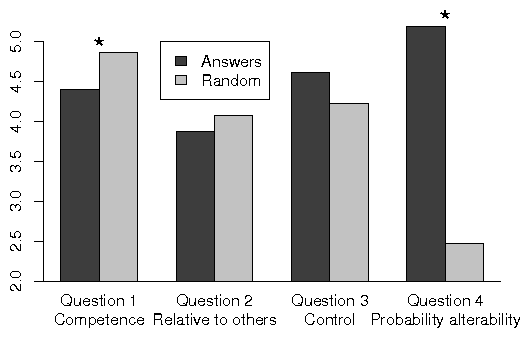fig5.png
Figure 5: Survey results in Experiment 3. All responses were made on a scale from 1 to 7. * p .05.

5  General Discussion

In three experiments, we assessed bet acceptance under ambiguity, where determination of the uncertain outcome was based on ability rather than a random event. This is a special case in the decision making literature, which has been treated both in terms of competence (Heath & Tversky, 1991) and control (Goodie, 2003). Control has been defined as a characteristic of the task wherein there are steps that could improve the probability of a favorable outcome. Competence is an interactive property of both the task and the individual, wherein improvement is possible and the participant has achieved it. According to the control hypothesis, it is the possibility of improvement that makes a difference.
In Experiment 1, using representative sampling in single domains, and with all statistical properties of bets held constant between groups, participants consistently accepted more bets when betting on their answers than when betting on random events. At all confidence levels in all experiments, those betting on their answers bet more frequently than those betting on a random event. These results provided strong support for the role of control in decision making.
In Experiment 2, overall bet acceptance was closely correlated with accuracy when assessed across the groups that were exposed to questions in differing domains. Such a correlation is the essential claim of the competence hypothesis. However, the trend of bet acceptance increasing with accuracy was not observed at the group level when acceptance was conditionalized on confidence. At the individual level, we found a significant correlation between accuracy and intercept within groups in Experiment 2b but not Experiment 2a.
In Experiment 3, as in Experiment 1, those betting on their own knowledge bet considerably more frequently than those betting on events that were identical in every statistical way but appeared random. Survey results indicated a large difference between the groups in the perception of control as defined here and a marginally significant effect on responding to the concept "control." We found no difference between groups in perceptions of the concept "competence" or its social-comparative definition.

5.1  Competence or control?

The current results provide strong support for the effect of control across a spectrum of degrees of competence, although there was also some degree of evidence in support of an effect of competence. Experiments 1 and 3 showed strong effects of control on risk acceptance. Importantly, those experiments used the question domains of city population and state population, which proved to be among the domains with the lowest accuracy in Experiment 2. The average accuracy using these two question domains was less than .75, lower than other domains. Yet, participants consistently chose to bet on them much more frequently than on equivalent random events. This provides evidence for the effect of control even when competence is relatively low. This supports the theoretical underpinning of control (Skinner, 1996) that people demonstrate more persistence and initiative when control prevails, perhaps to enhance future outcomes in domains where the likelihood of success can be increased.
In Experiment 3, the perceptions of participants suggested that the manipulation that had a profound effect on bet acceptance also affected probability alterability and, to an extent that was only marginally statistically significant, the term "control." This may be attributable at least in part to low accuracy; perhaps participants betting on their own answers would have rated competence higher in a similar setting but with easier questions. The conclusion remains, however, that control increases risk taking, even when competence is relatively low. These results are analogous to Cohen, Dearnaley, and Hansel's (1956) finding that inexperienced and experienced bus drivers assess future risky driving maneuvers similarly; both groups of drivers accept risk at a relatively similar rate.
We also found evidence to favor the competence hypothesis - that is, people accept risk more often when they perceive themselves to be competent than when they do not. In Experiment 2, bet acceptance at the group level correlated extremely closely with accuracy. However, when we controlled for the correlation between confidence and bet acceptance by examining bet acceptance curves, we found no group-level correlation between the intercept (overall elevation) of the betting curves and average accuracy within groups and only limited correlation at the individual level.
The present experiments utilized questions drawn from single domains, which allowed for a more accurate assessment of true confidence within that given set of questions than when utilizing questions drawn from mixed domains (as in Goodie, 2003). In that study, bet acceptance was low (Experiments 1 and 2) and lower than bet acceptance on matched random events (Experiment 3) at low levels of confidence. However, when low competence domains are removed in tests using single domains, bet acceptance at the lowest levels of confidence increases. The comparison between the present experiments and those of Goodie (2003) thus provides support for the competence hypothesis.

5.2  Why did the present studies find less strong evidence for the competence hypothesis?

The evidence to support the competence hypothesis was less strong in the present studies than in those of Heath and Tversky (1991). Perhaps the most striking finding of Heath and Tversky's studies came in their Experiment 4, where participants who perceived themselves as competent in one domain but incompetent in another consistently preferred to bet on a random event over an event of matched probability in the domain of incompetence. We didn't observe such an effect in these studies - any time participants could bet on their answers, they were considerably more prone to do so than bet on a random event, even when their answers were not terribly competent.
Why did this difference emerge? The answer may relate to a special feature of Heath and Tversky's sample. They sought participants who felt themselves of above-average competence in either football or political prediction, and also of below-average competence in the other domain. Of 110 participants they screened, 25 (23 percent) fit this criterion and constituted the sample. (Two of the 25 selected participants declined to participate.) If participants were well calibrated in evaluating their own abilities, and if these ratings were independent of each other, then half of all screened participants would fall on opposite sides of the median on the two measures. But less than a quarter satisfied the criterion. Most of the screened participants self-evaluated on the same side of the median for both tasks and were thus excluded. The data reflected only the rather small minority who placed themselves on opposite sides of the median for the two tasks. This could reveal participants who feel unusually weak competence in the weak area; it could reflect an individual difference that led these subjects, in contrast with the majority, to self-evaluate divergently in different domains. The larger effect observed by Heath and Tversky could also be attributable to their use of within-subjects designs, which may highlight comparisons among the three kinds of bets they employed.

5.3  Probability weighting and control

Goodie (2003) suggested that, within the framework of prospect theory (Kahneman & Tversky, 1979), the effect of control on decision making might most fruitfully be attributed to an effect on the probability weighting function considered from the perspective of the model offered by Gonzalez and Wu (1999). This model in turn relied on advances of Tversky and Wakker (1995) and Fox and Tversky (1995), demonstrating the psychological plausibility and empirical validity of considering a weighting function based on uncertain outcomes. These demonstrations culminated in a two-stage model (Fox & Tversky, 1998) wherein subjective probabilities elicited in a first stage can be weighted in a second stage in a comparable manner to objective (known) probabilities. The present studies adhered to this procedural framework.
In the studies of Goodie (2003), bet acceptance was an interactive function of confidence and control, such that participants accepted less often with control at low probabilities and more often with control at high probabilities. Goodie attributed this to an effect on the discriminability of probabilities. In the current experiments, no such interaction was evident: participants accepted more often with control than without across the entire spectrum of subjective probability. Thus, in the terms of Gonzalez and Wu's (1999) model, the effect of control may be better attributed to attractiveness. In short, people accept more risk under conditions of control than under conditions of no control. The idea of making weighting functions sensitive to properties of the setting other than perceived probability is not new. Kilka and Weber (2001) suggested that the probability weighting function should be "source dependent," which in their study reflected the degree of competence participants perceived in the domain of the uncertain judgment. The present experiments suggest that control may be a relevant and systematic dimension guiding the source dependence of the weighting function.

5.4  The importance of control

Natural decisions often contain an element of ability across domains. Examples of this include business-related decisions such as those in organizational management (Forlani, 2002; Hiller & Hambrick, 2005), marketing (White, Varadarajan, & Dacin, 2003), and investment (Fellner, Guth, & Maciejovsky, 2004); personal decisions such as mate selection (Hinsz, Matz, & Patience, 2001) and child rearing (Pridham, Denney, Pascoe, Chiu, & Creasey, 1995); health-related decisions such as dieting, exercise, diagnosis and treatment; law-related decisions such as regulation and jury decision making (Weinstock & Flaton, 2004), and even union leaders assessing random events, fictional elections and real elections (Maffioletti & Santoni, 2005). In all these cases, skill matters: some individuals can make systematically better decisions than others with more favorable consequences, and each individual can take steps to make better decisions. The effect of controllable situations on decision-making is an important aspect of decisions to study.
In one domain where control is present, March and Shapira (1987) famously cautioned decision theorists that organizational managers view the risks they take as being fundamentally different from gambling. To the extent this is true, it diminishes the applicability to management settings of the wealth of empirical decision research using real or hypothetical lottery pulls, rolls of dice, or poker chips drawn from bookbags. March and Shapira conclude, a bit cynically, that the distinction is a matter of "managerial conceit." In their view, managers suppose that the risks they take are different from (and better than) gambling because they are trained by societal norms to think so and also because among managers whose decisions have coincidentally succeeded, just as among a convention of lottery winners, the relative rate of winning is greater than the odds that are built into the game.
The present results build on March and Shapira's conclusion that the norms of society and the conceits of managers play a role in managerial decision making. In managerial settings and many other settings where control prevails - that is, where one's actions are thought to make a difference in the probability of success - the control itself makes a difference in decision making.
More generally, the control hypothesis has both positive and negative implications for applied decision making. The positive implication is that people may be expected to adopt a relatively broad horizon, sacrificing short-term expected value for the opportunity to learn and develop skill that will enhance future prospects. The negative implication is that, in cases where relatively short-term consequences are major - for example, when it is important not just to learn for the future but to manage the current organizational challenge, treat the current patient successfully, or win the current war - people may be excessively willing to accept risk even when they know they are incompetent.

5.5  Limitations and future directions

These results may have been different if participants in the Random groups were told that they were being given a bet concerning another participant's answer and confidence assessment. However, one might suspect that posing bets to participants in this manner may instead measure a different, unintended construct, such as skepticism in others' knowledge or social comparison (Moore & Kim, 2003).
Also the current studies only offered bets whose probabilities of winning were above 50%. This carries at least two limitations. First, of course, half the probability spectrum is excluded. Second, the excluded half is the lower half, and thus the many low-probability events that are the subject of much research cannot be directly addressed. However, although the range excludes half of the numerical range between 0 and 1, it reflects the full range of competence from random choice to full knowledge within a binary choice paradigm, and a wide swath of this possible range was encompassed within the present studies.
It is possible that participants would be motivated to perform differently for money than they did for points in these studies. The findings of Goodie and Fantino (1995) suggest that there may be little effect. In the end, we subscribe to the prescription to do it both ways (Hertwig & Ortmann, 1999), and have found essentially similar results using monetary incentives (Young, Goodie, & Hall, 2007).

5.6  Conclusions

The present results provide evidence that control affects decision making apart from competence. There is also new evidence that competence affects decision making. The unique contribution of control to decision making has important theoretical and applied implications, suggesting that decisions may be influenced by the opportunity to improve at tasks that can be learned, even at short-term expected loss, in order to create more advantageous prospects in the future.

References

Baron, J. (2000). Thinking and deciding, (Third Ed.) Cambridge University Press.
Burger, J. M., & Schnerring, D. A. (1982). The effects of desire for control and extrinsic rewards on the illusion of control and gambling. Motivation & Emotion, 6, 329-335.
Campbell, W. K., Goodie, A. S., & Foster, J. D. (2004). Narcissism, confidence and risk attitude. Journal of Behavioral Decision Making, 17, 297-311.
Chau, A. W., & Phillips, J. G. (1995). Effects of perceived control upon wagering and attributions in computer blackjack. Journal of General Psychology, 122, 253-269.
Chow, C. C., & Sarin, R. K. (2001). Comparative ignorance and the Ellsberg Paradox. Journal of Risk and Uncertainty, 22, 129-139.
Cohen, J., Dearnaley, E. J., & Hansel, C. E. M. (1956). Risk and hazard: Influence of training on the performance of bus drivers. Operational Research, 7, 67-82.
Ellsberg, D. (1961). Risk, ambiguity, and the Savage axioms. Quarterly Journal of Economics, 75, 643-669.
Fellner, G., Guth, W., & Maciejovsky, B. (2004). Illusion of expertise in portfolio decisions: An experimental approach. Journal of Economic Behavior and Organization, 55, 355-376.
Forlani, D. (2002). Risk and rationality: The influence of decision domain and perceived outcome control on managers' high-risk decisions. Journal of Behavioral Decision Making, 15, 125-140.
Fox, C. R., & Tversky, A. (1995). Ambiguity aversion and comparative ignorance. Quarterly Journal of Economics, 110, 585-603.
Fox, C. R., & Tversky, A. (1998). A belief-based account of decision under uncertainty. Management Science, 44, 879-895.
Fox, C. R., & Weber, M. (2002). Ambiguity aversion, comparative ignorance, and decision context. Organizational Behavior and Human Decision Processes, 88, 476-498.
Frisch, D., & Baron, J. (1988). Ambiguity and rationality. Journal of Behavioral Decision Making, 1, 149-157.
Gigerenzer, G. (1991). How to make cognitive illusions disappear: Beyond "heuristics and biases." In W. Stroebe & M. Hewstone (Eds.), European review of social psychology, (Vol. 2, pp.83-115). Chichester, England: Wiley.
Gilovich, T., Vallone, R., & Tversky, A. (1985). The hot hand in basketball: On the misperception of random sequences. Cognitive Psychology, 17, 295-314.
Gonzalez, R., & Wu, G. (1999). On the shape of the probability weighting function. Cognitive Psychology, 38, 129-166.
Goodie, A. S. (2003). Paradoxical betting on items of high confidence with low value: The effects of control on betting. Journal of Experimental Psychology: Learning, Memory, and Cognition, 29, 598-610.
Goodie, A. S., & Fantino, E. (1995). An experientially derived base-rate error in humans. Psychological Science, 6, 101-106.
Heath, C., & Tversky, A. (1991). Preference and belief - ambiguity and competence in choice under uncertainty. Journal of Risk and Uncertainty, 4, 5-28.
Hertwig, R., & Ortmann, A. (2001). Experimental practices in economics: A methodological challenge for psychologists? Behavioral and Brain Sciences, 24, 383-403.
Hiller, N. J., & Hambrick, D. C. (2005). Conceptualizing executive hubris: The role of (hyper-) core self-evaluations in strategic decision-making. Strategic Management Journal, 26, 297-319.
Hinsz, V. B., Matz, D. C., & Patience, R. A. (2001). Does women's hair signal reproductive potential? Journal of Experimental Social Psychology, 37, 166-172.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47, 263-291.
Kilka, M., & Weber, M. (2001). What determines the shape of the probability weighting function under uncertainty? Management Science, 47, 1712-1726.
Koehler, J. J., Gibbs, B. J., & Hogarth, R. M. (1994). Shattering the illusion of control: Multi-shot versus single-shot gambles. Journal of Behavioral Decision Making, 7, 183-191.
Langer, E. J. (1975). The illusion of control. Journal of Personality and Social Psychology, 32, 311-328.
Maffioletti, A., & Santoni, M. (2005). Do trade union leaders violate subjective expected utility?: Some insights from experimental data. Theory and Decision, 59, 207-253.
March, J. G., & Shapira, Z. (1987). Managerial perspectives on risk and risk-taking. Management Science, 33, 1404-1418.
Moore, D. A., & Kim, T. G. (2003). Myopic social prediction and the solo comparison effect. Journal of Personality and Social Psychology, 85, 1121-1135.
Nelson, T. O., & Narens, L. (1980). Norms of 300 general-information questions: Accuracy of recall, latency of recall, and feeling-of-knowing ratings. Journal of Verbal Learning and Verbal Behavior, 19, 338-368.
Pridham, K., Denney, N., Pascoe, J., Chiu, Y. M., & Creasey, D. (1995). Mothers solutions to child-rearing problems - conditions and processes. Journal of Marriage and the Family, 57, 785-799.
Seligman, M. E. P. (1975). Helplessness: On depression, development, and death. San Francisco: Freeman.
Sieck, W. R., & Arkes, H. R. (2005). The recalcitrance of overconfidence and its contribution to decision aid neglect. Journal of Behavioral Decision Making, 18, 29-53.
Skinner, E. A. (1996). A guide to constructs of control. Journal of Personality and Social Psychology, 17, 549-570.
Tversky, A., & Wakker, P. P. (1995). Risk attitudes and decision weights. Economectrica, 63, 1255-1280.
Weinstock, M. P., & Flaton, R. A. (2004). Evidence coverage and argument skills: Cognitive factors in a juror's verdict choice. Journal of Behavioral Decision Making, 17, 191-212.
White, J. C., Varadarajan, P. R., & Dacin, P. A. (2003). Market situation interpretation and response: The role of cognitive style, organizational culture, and information use. Journal of Marketing, 67, 63-79.
Young, D. L., Goodie, A. S., & Hall, D. B. (2007). Modeling effects of perceived control on the probability weighting function. Unpublished manuscript, University of Georgia.

Footnotes:

1This research was supported by National Institutes of Health research grant MH067827. Address correspondence to: Adam S. Goodie, Department of Psychology, University of Georgia, Athens, GA 30602-3013; Phone 706-542-6624; Fax 706-542-3275; Email goodie@uga.edu
2State population was taken as the 1999 Census Bureau estimate, and population density was the ratio of population to land area. Questions involving city comparisons used the 50 largest metropolitan areas in the continental U.S., to eliminate the confusion involved in considering driving distance to San Juan, Puerto. City population was taken as the population of the entire metropolitan area as identified by the Census Bureau (this was made clear in the instructions), and driving distance was the distance to the central city.
3In their empirical studies, Heath and Tversky (1991) established two levels of competence, but they did not claim that competence is an inherently binary construct. We take it to be a variable that can have several levels, and that may be continuous.

File translated from TEX by TTH, version 3.67.
On 14 Jun 2007, 16:19.