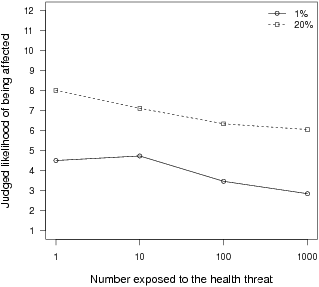
| Figure 1: The mean intuitive likelihood judgment as a function of the number of people exposed to the health threat and the probability of being affected in Experiment 1. The results are collapsed across the bacteria and carcinogen scenarios. |
Judgment and Decision Making, vol. 4, no. 6, October 2009, pp. 436-446
From group diffusion to ratio bias: Effects of denominator and numerator salience on intuitive risk and likelihood judgmentsPaul C. Price* and Teri V. Matthews |
The group-diffusion effect is the tendency for people to judge themselves to be less likely to experience a negative outcome as the total number of people exposed to the threat increases — even when the probability of the outcome is explicitly presented (Yamaguchi, 1998). In Experiment 1 we replicated this effect for two health threat scenarios using a variant of Yamaguchi’s original experimental paradigm. In Experiment 2, we showed that people also judge themselves to be less likely to be selected in a lottery as the number of people playing the lottery increases. In Experiment 3, we showed that explicitly presenting the number of people expected to be selected eliminates the group-diffusion effect, and in Experiment 4 we showed that presenting the number expected to be affected by a health threat without presenting the total number exposed to the threat produces a reverse effect. We propose, therefore, that the group-diffusion effect is related to the ratio bias. Both effects occur when people make risk or likelihood judgments based on information presented as a ratio. The difference is that the group-diffusion effect occurs when the denominator of the relevant ratio is more salient than the numerator, while the ratio bias occurs when the numerator is more salient than the denominator.
Keywords: risk judgment, probability judgment, group-diffusion effect,
ratio bias.
In many situations, there is “safety in numbers.” A person in a group is less susceptible to a wide variety of threats than a person who is alone. Consider, for example, a traveler who is walking in a strange city at night. If this person is in a group, he or she is probably less likely to get lost, less likely to be mugged, and more likely to receive help in the event that he or she twists an ankle. However, there are many other kinds of threats for which being part of a group makes no difference. Imagine, for example, a traveler who eats at a local restaurant. If the food in the restaurant were found to be contaminated with E. coli, then the person would be just as likely to get sick after dining in a group as after dining alone. There is evidence, however, that people tend to confuse the latter type of situation with the former. That is, people sometimes perceive an illusory safety in numbers.
In the first demonstration of this effect, Yamaguchi (1998) presented college students with one of six scenarios in which they were exposed to a threat (e.g., a carcinogen, a financial risk) and asked them to judge the probability that they would experience an associated negative outcome. One of his scenarios, for example, read as follows.
An infectious disease is prevalent in a foreign city. The disease comprises a fever and temperatures of over 39 degrees for more than a week together with severe diarrhea. Although the death rate is not high, the disease has after-effects such as total hair loss. The city authorities are afraid of losing tourists from abroad and have kept the matter confidential. A group of 10 Japanese tourists including yourself has arrived in the city and plan to stay for one week. How likely do you think it is that you will catch the disease if you stay as planned for one week?
For each scenario, there was an alone condition in which the participant was exposed to the threat alone (“You have arrived in the city …”), a small-group condition in which the participant was one of 10 people exposed, and a large-group condition in which anywhere from 100 to 1 million people were exposed, depending on the scenario.
Across all the scenarios, there was a strong tendency for participants to give lower probability judgments as the number of people exposed to the threat increased. Furthermore, the function relating group size to perceived risk was roughly logarithmic. There was a large drop in perceived risk from the alone to the small-group condition, with a smaller drop from the small-group to the large-group condition. Yamaguchi (1998) referred to this as the group-diffusion effect and he proposed that it occurs because people use an interdependence heuristic. They apply the general rule that “I am safer in a larger group” even when group size is irrelevant. According to Yamaguchi, the interdependence heuristic could have evolved as the cognitive concomitant of the motivational mechanisms that lead humans — and many other animals — to form and maintain social groups. Of course, these mechanisms evolved because there often is safety in numbers. Individuals in groups are better able to fend off attacks, find mates, find or create shelter, and forage successfully. But the group-diffusion effect is the result of over-applying this generally useful rule.
Our purpose in conducting the present research on the group-diffusion effect was twofold. First, we wanted to replicate it, because there have been only two published studies on it since Yamaguchi’s (1998), which was conducted in Japan. One replicated the basic effect in Hong Kong (Ho & Leung, 1998). The other was only partially successful in replicating the effect in the United States (Chua, Yamaguchi, & Yates, 2001, described in Yamaguchi et al., 2008), with the group-diffusion effect being observed for only two of the six scenarios tested. These results leave open the possibility — as Yamaguchi himself pointed out — that culture might play a role in the group-diffusion effect. Because both Japan and Hong Kong are culturally more collectivist than the United States (e.g., Triandis & Tramifow, 2001), participants in those countries might be more attentive to the number of people exposed to a threat or be more likely to apply the interdependence heuristic, perhaps because of their greater sense of collective control as opposed to individual control (Yamaguchi, Gelfand, Ohashi, & Zemba, 2005; Yamaguchi et al., 2008). It is important, therefore, to replicate the group-diffusion effect in an individualistic culture such as that of the United States.
Our second purpose in conducting this research was to consider an alternative explanation of the group-diffusion effect. Specifically, we thought it might be the result of people’s attending to and weighting the number of people exposed to the risk more heavily than other information in making their likelihood judgments. Consider two scenarios. In one, 1 person is expected to be taken ill out of 10 people exposed to a virus. In the other, 10 people are expected to be taken ill out of 100 people exposed. The probability that any individual will be taken ill is given by the ratio of the number of people expected to be affected to the number of people exposed, and of course the two probabilities in this example are the same (1/10 = 10/100 = 10%). However, if people attend to and weight the number of people exposed (the denominator of the fraction) more than the number expected to be affected (the numerator), then they would perceive lower risk when the number of people exposed is 100 than when it is 10. Note that there is no motivational component to our theory. People do not attend to and weight the denominator more than the numerator because it makes them feel safe. They attend to and weight it more because it is more attentionally salient.
A potential problem with this idea is that there is considerable research on a phenomenon called the ratio bias that seems to show just the opposite. When reasoning about likelihoods based on ratios, people attend to and weight numerators more than denominators. For example, Denes-Raj and Epstein (1994, following Piaget & Inhelder, 1951/1975) asked people to choose between two gambles. In one, they would win if they selected a red jelly bean from a bin containing 10 jelly beans, where one of them was red. In the other, they would win if they selected a red jelly bean from a bin containing 100 jelly beans, where between 5 and 9 of them were red. Surprisingly, many people preferred to select from the second bin, implying that they were focusing on the greater number of red jelly beans in that bin (for additional examples, see also Dale, Rudski, Schwarz, & Smith, 2007; Denes-Raj, Epstein, & Cole, 1995; Reyna & Brainerd, 2008). Yamagishi (1997) has shown something similar in the domain of risk perception. His participants judged the riskiness of various causes of death when the death rates were presented as ratios, and they appeared to attend to and weight the numerators more than the denominators. For example, they judged the risk of dying of cancer to be greater when told that it kills 1,286 people out of 10,000 than when told that it kills 24.14 people out of 100. The ratio bias has also been shown to influence the elicitation of health-state utilities (Pinto-Prades, Martinez-Perez, & Abellán-Perpiñán, 2006) and the perceived guilt of a defendant based on DNA evidence (Koehler & Macchi, 2004).
Our proposal, however, is that, although people attend to and weight the numerator more than the denominator in many situations, they do the opposite in others. Furthermore, this is mainly a consequence of the relative salience of the numerator and denominator. In terms of the classic jelly bean scenario that has been used to demonstrate the ratio bias, people might exhibit a group-diffusion effect — judging the likelihood of selecting a red jelly bean to be lower when there are 100 jelly beans in the bin than when there are 10 — if their attention is drawn primarily to the total number of jelly beans rather than the number of red ones. One way to do this might be to present the number of red jelly beans implicitly rather than explicitly by giving the total number of jelly beans along with the probability of selecting a red one (10%). Consider the analogous situation described in the following letter to a popular media columnist who answers people’s mathematical, scientific, and technical questions (vos Savant, 2006).
Family and friends have ganged up on me, but we agree to believe what you say. I say the odds of winning a six-number lottery (in which you choose the numbers) are the same whether 100 or 100,000 tickets are sold. They say the chances are better if only 100 are sold. Who’s right?
Although the chances of winning are the same regardless of how many tickets are sold, the letter writer’s family and friends appear to be influenced by that number — perhaps because it is the most salient one presented explicitly in the scenario.
The scenarios used by Yamaguchi (1998) are similar to our hypothetical jelly bean example and the lottery example above in that they seem to draw attention to the denominator of the relevant ratio — the number of people exposed to the threat. While all six of Yamaguchi’s scenarios prominently featured the number of people exposed to the threat, none of them explicitly presented the number of people expected to be affected. In one of his scenarios (and also in the scenarios of Ho & Leung, 1998), the probability of the negative outcome was presented (e.g., a 15% chance of developing cancer), but, given the difficulty that people have in understanding single-event probabilities (Gigerenzer, 1994), it seems likely that the number exposed to the threat remained a highly salient piece of information — certainly more salient than the non-presented or implicitly presented number of people expected to be affected.
Similar ideas have been explored by other researchers, although not in connection with the group-diffusion effect. For example, Stone et al. (2003) speculated that the greater impact of certain graphical risk communication methods occurs because these graphical methods emphasize the number of people expected to be affected more than the number exposed. For example, a bar graph that compared the gum-disease risk associated with two brands of toothpaste in terms of the number of people expected to be affected produced relatively large differences in what people were willing to pay for the two products (Stone, Yates, & Parker, 1997). However, Stone et al. (2003) found that a stacked bar graph that shows both the number expected to be affected and the total number who use each toothpaste produced much smaller differences on par with the differences produced by presenting the risks in terms of probabilities.
Bonner and Newell (2008), however, found no effect of a conceptually similar manipulation. They presented people with information about various causes of death in terms of the number of people who die per day from that cause or the number who die per year. For example, the frequency of death from cancer in Australia was presented as 100 deaths per day or as 36,500 deaths per year. In essence, these are ratios in which the number of deaths is the numerator and the time period is the denominator. These researchers also included a condition in which the number of deaths (the numerator) was made more salient (e.g., “100 people in Australia die every day from cancer.”) and a condition in which the time frame (the denominator) was made more salient (“Every day in Australia 100 people die from cancer.”). Consistent with research on the ratio bias, they found that most people rated the causes of death riskier in the per-year condition than in the per-day condition — with a minority showing the opposite effect. The salience manipulation, however, had no effect.
We began our research by replicating the group-diffusion effect on college students in the United States with two health scenarios to be sure that it occurs with participants from a more individualistic culture. We continued by replicating it again in Experiment 2, but in a new context. Instead of health-threat scenarios, we used lottery scenarios in which participants had a chance to lose or win money. Our rationale was that if participants exhibited a group-diffusion effect for a positive outcome (i.e., winning money), then it is unlikely that the effect is the result of an interdependence heuristic that is applied in response to a threat. Such a result would be consistent, however, with the idea that people simply attend to and weight the denominator of the relevant ratio more than the numerator. In Experiment 3, we show that the group-diffusion effect is eliminated when we change the scenarios slightly to include an explicit presentation of the numerator of the relevant ratio as well as the denominator. Finally, in Experiment 4, we show that explicitly presenting the numerator but not the denominator produces an effect in the opposite direction — a ratio bias. All of these results are consistent with our proposal that the group-diffusion effect is a result of people’s attending to and weighting the denominator of the relevant ratio more than the numerator. They also demonstrate a theoretical connection between the group-diffusion effect and the much better known ratio bias.
We decided to replicate the group-diffusion effect using a variant of Yamaguchi’s (1998) paradigm. The primary differences are that we used a within-subjects design in which participants responded to several scenarios that varied systematically in terms of the health threat under consideration, the objective probability of the negative outcome, and the number of people exposed to the threat. Second, we asked participants to make non-numeric likelihood judgments on a 12-point scale rather than numeric judgments on a standard percentage scale. The reason is that some non-normative likelihood judgment phenomena — such as the alternative-outcomes and dud-alternative effects — are observed only when people make non-numeric judgments (Windschitl & Krizan, 2005). This is probably because numeric response scales prompt people to treat their task as a mathematical one with a precise answer to be calculated, which they dutifully calculate. Because we are more interested in people’s intuitions about risk and likelihood, we decided to use the non-numeric response format.
The participants were 31 students at California State University, Fresno, who participated in return for partial credit in an introductory psychology course. There were 20 women, 6 men, and 5 participants whose sex was not recorded.
Participants completed a questionnaire with 16 short items loosely based on the scenarios used by Yamaguchi (1998). Eight of the items concerned a bacteria scenario and had the following general form.
Imagine that you are one of N people eating at a restaurant. Afterward, you find out that you were exposed to a certain kind of bacteria in the food. Furthermore, medical experts say that people exposed to these bacteria have a P probability of becoming seriously ill as a result.
The other eight items concerned a carcinogen scenario and had the following general form.
Imagine that you are one of N people in your neighborhood whose drinking water is found to be contaminated with a cancer-causing chemical. Scientists say that people exposed to this chemical have a P probability of developing liver cancer.
The number of people exposed to the health threat, N, was varied systematically across the items. It was either 1, 10, 100, or 1000. When N was 1, the wording of the scenario was changed slightly to seem more natural (e.g., “Imagine that you are eating alone in a restaurant.”). The objective probability of experiencing the threat, P, was also varied systematically across the items; it was either 1% or 20%. Thus, the items represented all 16 possible combinations of the number of people exposed (1, 10, 100, or 1000), the objective probability (1% or 20%), and the threat (bacteria or carcinogen). The items were arranged on the questionnaire in a randomized order, and a second form was created by reversing the order of the items.
The question that participants responded to for each item was of the form, What is your “gut feeling” about your chance of [becoming seriously ill / developing liver cancer]? They responded by circling one of 12 horizontally arrayed asterisks, anchored with the labels Extremely Poor Chance on the left-hand side and Extremely Good Chance on the right-hand side. Participants completed the questionnaire in small, non-interacting groups. They read a short set of instructions that described the use of the response scale and then completed the 16 items at their own pace.

Figure 1: The mean intuitive likelihood judgment as a function of the number of people exposed to the health threat and the probability of being affected in Experiment 1. The results are collapsed across the bacteria and carcinogen scenarios.
Each response was coded as an integer from 1 to 12, with lower numbers indicating a lower chance of experiencing the negative outcome. Despite the instructions, two participants circled an anchor label or a cluster of asterisks — rather than a single asterisk — for each item. These participants were dropped from the analyses. Two others circled an anchor label rather than an asterisk for just a few items. On these items, we coded the response as the most extreme response at that end of the scale (i.e., 1 or 12). The final analyses, therefore, were based on the responses of 29 participants.
Figure 1 presents the mean gut-feeling likelihood judgment as a function of the number exposed to the threat, separately for the two objective probabilities. As the figure shows, there was a clear group-diffusion effect, with participants judging their chances of experiencing the negative outcome to be lower as the number of people exposed to the threat increased.
To confirm this interpretation, we conducted a repeated-measures analysis of variance (ANOVA) with the number exposed, objective probability, and health threat as within-subjects factors, and item order as a between-subjects factor. There was no main effect of health threat, F(1,27) = 0.49, p = .49, or item order, F(1,27) = 0.01, p = .92, which is why the data are collapsed across these factors in Figure 1. Not surprisingly, there was a linear effect of objective probability, F(1,27) = 93.53, p < .001. Most importantly, for our purposes, is that there was a linear effect of the log of the group size, F(1,27) = 35.80, p < .001 — a group-diffusion effect. The only significant interaction was that among group size, threat, and item order, F(1,27) = 9.85, p = .004. Interactions involving item order are likely to be caused by participants’ responding differently to particular items when they happen to be near the beginning versus the end of the questionnaire. Because such effects are not relevant to our concerns here — and because they were inconsistent across the present studies — we do not discuss them further.
Recall that Bonner and Newell (2008) found evidence of individual differences in their study of ratio bias. While most of their participants judged causes of death to be riskier when they were presented in terms of the number dying per year, a significant minority showed the opposite effect. To look for such differences in the present experiment, we computed an effect for each participant by taking the simple correlation between the log of the group size and his or her likelihood judgments. These correlations ranged from –.70 to +.07, with a median of –.30. Only one participant had a positive correlation. Thus, we found no evidence of individual differences in the direction of the effect.
In summary, we convincingly replicated the group-diffusion effect using an American sample in Experiment 1. Again, our procedure differed from Yamaguchi’s (1998) in that we used a within-subjects design and a non-numeric response format. Of course it would be interesting to explore the extent to which these differences affect the results, but we chose to explore whether these results are best explained by the idea that people use an interdependence heuristic or by the idea that they are exhibiting a salience-based tendency to attend to and weight the denominator of the relevant ratio more than the numerator.
If the group-diffusion effect is the result of people’s using an interdependence heuristic, then it seems reasonable that they would exhibit the effect when judging their risk of experiencing negative outcomes as in Experiment 1. But what if people were to judge the likelihood that they would experience positive outcomes? We can think of two possibilities. One is that such situations would fail to cue the interdependence heuristic at all so that there would be no effect of the number exposed. A second possibility is that people would continue to feel safer in larger groups and that this positive feeling would cause them to judge themselves to be more likely to experience positive events — the opposite of a group-diffusion effect. On the other hand, if the group-diffusion effect is the result of a salience-based over-weighting of the number exposed, then people should judge themselves to be less likely to experience positive events, in addition to negative events, as the number exposed increases.
In Experiment 2, therefore, we used items that featured a lottery scenario. Participants imagined that they were in a room with N people and that each person had a P probability of being selected. For some items, the outcome of being selected was that they lost $50. For other items, the outcome was that they won $50. Again, our attentional explanation predicts that people should judge their likelihood of both losing and winning to decrease as the number of people participating in the lottery increases.
The participants were 38 students at California State University, Fresno, who participated in return for partial credit in an introductory psychology course. There were 21 women, 8 men, and 2 additional participants whose sex was not recorded.
Again, participants completed a questionnaire with 16 short items, all of the following general form.
Picture yourself as one of N people in a room. Everyone in the room has a P chance of being randomly selected to [win / lose] $50.
The 16 items represented the 16 different combinations of the number of people in the lottery (1, 10, 100, or 1000), the objective probability of being selected (1% or 20%), and the outcome (winning $50 or losing $50). The items were arranged on the questionnaire in a randomized order, and a second form was created by reversing the order of the items. For each item, participants responded to the question, What is your gut feeling” about your chance of being selected? They responded by circling one of 11 horizontally arrayed asterisks, anchored with the labels Extremely Poor Chance on the left-hand side and Extremely Good Chance on the right-hand side. The change from a 12-point scale in Experiment 1 to an 11-point scale in the rest of the experiments was incidental.
Each response was coded as an integer from 1 to 11, with lower numbers indicating a lower chance of experiencing the outcome. Again, two participants circled an anchor label for a small number of items and their responses for these items were coded as the most extreme response at that end of the scale (i.e., 1 or 11).
Figure 2 presents the mean likelihood judgment as a function of the number of people in the lottery, separately for the two objective probabilities and two outcomes. As the figure shows, there appears to have been a group-diffusion effect, with participants tending to judge themselves less likely to be selected as the number of people in the lottery increased. An ANOVA analogous to that described previously confirmed that there was no main effect of outcome, F(1,33) = 0.15, p = .70, or item order, F(1,33) = 0.09, p = .77. There was a linear effect of the objective probability, F(1,33) = 35.41, p < .001, and also a linear effect of the log of the number of people in the lottery, F(1,33) = 40.27, p < .001, confirming that there was an overall group-diffusion effect.
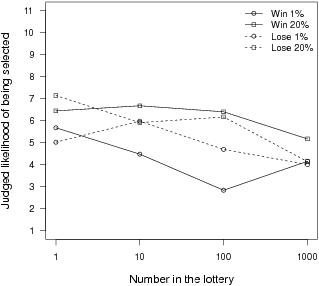
Figure 2: The mean intuitive likelihood judgment as a function of the number of people in the lottery, the probability of being selected, and the outcome of the lottery in Experiment 2.
There were also significant interactions between objective probability and outcome, F(1,33) = 6.15, p < .02, and among the number of people, objective probability, and outcome, F(1,33) = 4.85, p = .003. These seem to indicate that participants were more sensitive to the difference between the two probabilities for winning than for losing — and especially when there were 100 people in the lottery — although it is not immediately clear why this should be.
The evidence for individual differences in the direction of the effect
in this experiment is merely suggestive. Under the lose condition,
the simple correlations between the log of the group size and each
participant’s likelihood judgments ranged from –.95 to +.27, with a
median of
–.24. Only five of those correlations were positive and
only one exceeded .15. Thus, the effects were fairly consistent in
the lose condition. Under the win condition, however, the
correlations ranged from –.96 to +.64, with a median of –.02. To
examine the possibility of individual differences more closely —
especially in the win condition — we plotted individual
participants’ p values in Figure 3. Each p value is shown in
terms of both the proportion of p values expected to be less than or
equal to it and the proportion that was actually less than or equal
to it. For example, we would expect 5% of the p values
to be less than or equal to .05. Here a p value below .50 indicates a
negative correlation (a group-diffusion effect) and a p value
above .50 indicates a positive correlation (a ratio bias). Effects in
both directions would be indicated by a greater proportion of low
p values than expected (points appearing above the 1:1 diagonal on the
left) and a greater proportion of high p values than expected (points
appearing below the 1:1 diagonal on the right). The actual pattern,
however, shows no evidence of an effect in the opposite direction for
either the lose or win conditions.
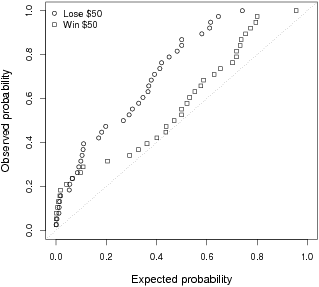
Figure 3: The proportion of individual participants’ p values that are less than or equal to the expected proportion for both the lose and win conditions in Experiment 2.
An alternative way of looking at individual differences involves examining the relationship between the size of the effect under the lose and win conditions across participants. To the extent that individual participants show a consistent group-diffusion effect across conditions, these variables should correlate highly. In fact, the correlation is surprisingly weak, r(36) = .12, p = .45. Figure 4 suggests that this might be because there was a distinct cluster of participants who had a substantial negative correlation under the lose condition but a substantial positive correlation under the win condition. This could represent a true “safety-in-numbers” effect for these participants. Being in a larger group caused them to give more optimistic judgments regardless of whether optimism meant a lower chance of losing or a higher chance of winning.
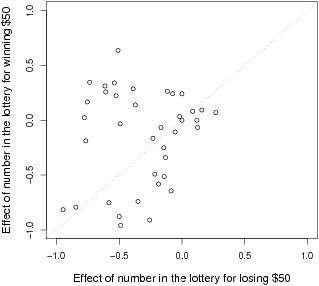
Figure 4: The relationship between the effect size under the lose and win conditions across participants in Experiment 2. The effect size is the simple correlation between the number of people in the lottery and the participant’s intuitive likelihood judgment.
Despite the suggestion of individual differences, the results of Experiment 2 are generally consistent with our salience explanation of the group-diffusion effect but inconsistent with Yamaguchi’s (1998) interdependence heuristic explanation. Experiment 3 was designed to test another straightforward implication of our explanation. If the way a scenario is presented calls as much attention to the number of people expected to be affected (the numerator of the relevant ratio) as to the number of people exposed (the denominator), then the group-diffusion effect should be eliminated. In Experiments 1 and 2, the numerator was not explicitly presented; it had to be inferred from the number exposed and the stated probability of being affected. In Experiment 3, we presented the numerator explicitly.
The participants were 43 students at California State University, Fresno, who participated in return for partial credit in an introductory psychology course. There were 33 women, 8 men, and 2 participants whose sex was not recorded.
Participants completed a questionnaire with 12 items of the following general form.
Picture yourself as one of N people in a room. n of the N people in the room will be randomly selected to [win / lose] $50.
In this experiment, N was either 10, 100, or 1000. (The structure of the task made it impossible to have a condition in which N was 1.) The value of n was chosen so that the probability of being selected was either 10% (e.g., n = 1 when N = 10) or 30% (e.g., n = 30 when N = 100). Note that we had to increase our lower probability from 1% to 10% in this experiment to avoid ratios of 0.10 out of 10. The 12 items, then, represented the 12 different combinations of the number of people in the lottery (10, 100, or 1000), the objective probability of being selected (10% or 30%), and the outcome (winning $50 or losing $50). The key is that participants were given the numerator (n) explicitly as opposed to having to infer it from N and P as in Experiments 1 and 2.
Again, the items were arranged on the questionnaire in a randomized order, and a second form was created by reversing the order of the items. For each item, participants responded to the same likelihood judgment question as in Experiment 2.
Each response was coded as an integer from 1 to 11, with lower numbers indicating a lower chance of experiencing the outcome. Five participants made unusable responses and were dropped from the analyses.
Figure 5 presents the mean likelihood judgment as a function of the number of people in the room, separately for the two objective probabilities and two outcomes. Again, there was no effect of winning versus losing, F(1,36) = 1.30, p = .26, or item order, F(1,36) = 0.05, p = .83, but there was a linear effect of the objective probability, F(1,36) = 35.83, p < .001. Most importantly — and unlike in Experiments 1 and 2 — there was no linear effect of the log of the group size, F(1,36) = 0.22, p = .64. Thus, explicitly including the numerator of the relevant ratio in addition to the denominator eliminated the group-diffusion effect, which is what we predicted based on our attentional explanation.
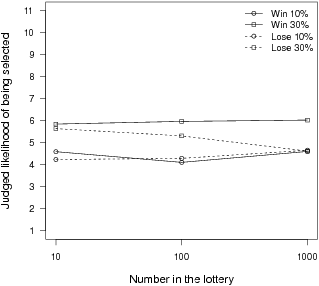
Figure 5: The mean intuitive likelihood judgment as a function of the number of people in the lottery, the probability of being selected, and the outcome of the lottery (winning vs. losing $50) in Experiment 3.
As in Experiment 2, there were also significant interactions between objective probability and outcome, F(1,36) = 7.02, p = .01, and among group size, objective probability, and outcome, F(1,36) = 6.16, p = .02. And again these seem to indicate that participants were more sensitive to the difference between the two probabilities for winning than for losing — especially for the larger group sizes.
Given the null effect of group size in Experiment 3, it is especially important to consider the possibility that there are individual differences in the direction of the effect that cancel each other out. Again, we computed the simple correlation between the log of the group size and each participant’s likelihood judgments separately for the lose and win conditions. In the lose condition, the correlations ranged from –.76 to +.82, with a median of –.12. In the win condition, the correlations ranged from –.92 to +.82, with a median of .00. Figure 6 shows, for individual participants’ p values in both the lose and win conditions, the proportion that would be expected to be less than or equal to that p value if there were no effect in either direction and the proportion that was actually less than or equal to it. Note that the observed values track the expected values quite closely, meaning that this appears to be a true null effect. The correlation between the effect size for the win and lose conditions across participants was somewhat higher than in Experiment 2, r(36) = .30, p = .07. And this time there was no indication of a subset of participants who were affected differently by the number of people in the room under the lose and win conditions.
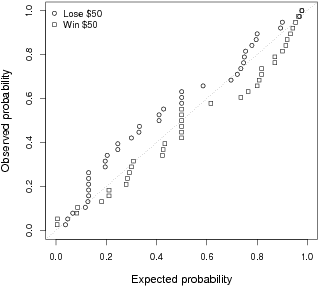
Figure 6: The proportion of individual participants’ p values that are less than or equal to the expected proportion for both the lose and win conditions in Experiment 3.
Experiments 1 through 3 have replicated the group-diffusion effect, shown that it occurs when people judge the risk of both negative and positive outcomes, and shown that explicitly presenting the numerator of the relevant ratio in addition to the denominator eliminates the effect. In Experiment 4, we addressed two issues. One is that we have not yet shown that the presence versus absence of information about the number of people expected to be affected determines whether or not we observe the group-diffusion effect in a single experiment in which all other factors are controlled. Experiment 2 demonstrated a group-diffusion effect when numerator information was not explicitly presented, while Experiment 3 failed to demonstrate an effect when both numerator and denominator information were explicitly presented. Although both experiments concerned losing and winning lotteries, the Experiment 2 scenarios explicitly presented the probability of being selected but the Experiment 3 scenarios did not. Experiment 4, therefore, included the denominator-only and numerator-plus-denominator conditions in the same study, while explicitly presenting the probability of being selected in both conditions. The second issue addressed by Experiment 4 is whether we can observe a reversal of the group-diffusion effect — a ratio bias — in a third condition in which we explicitly present only the numerator so that the denominator must be inferred.
In all three conditions, participants were given the probability of experiencing a negative health outcome. In the denominator-only condition, they were also given the number of people exposed to the threat but not the number expected to be affected, as in Experiments 1 and 2. In the numerator-plus-denominator condition, they were given both the number of people exposed and the number expected to be affected, similar to Experiment 3. In the numerator-only condition, they were given the number of people expected to be affected but not the number of people exposed. Our prediction was that we would observe a group-diffusion effect in the denominator-only condition, no effect in the numerator-plus-denominator condition, and a ratio bias in the numerator-only condition.
The participants were 88 students at California State University, Fresno, who participated in return for partial credit in a health psychology course or an introductory psychology course. There were 68 women, 16 men, and 4 participants whose sex was not recorded.
Participants completed a questionnaire with 12 items similar to those in Experiment 1. Participants were randomly assigned to one of three information conditions. In the denominator-only condition, the items were of the same general form as in Experiment 1. In the numerator-plus-denominator condition, the last sentence continued, “so [the medical experts] expect about n of the people to [become seriously ill / develop cancer],” where n was simply the specified percentage (P) of the N people exposed. In the numerator-only condition, the items still indicated the number of people expected to be affected, but they only indicated that “several” people were exposed instead of the precise number. In all three conditions, the number of people exposed to the health threat (N) was either 10, 100, or 1000, and the probability of being affected (P) was either 10% or 30%. These values, of course, determined the corresponding numbers of people expected to be affected (n). The 12 items, then, represented the 12 different combinations of the number of people exposed (N = 1, 10, 100, or 1000), the objective probability of being affected (P = 10% or 30%), and the health threat (bacteria or carcinogen).
Again, the items were arranged on the questionnaire in a randomized order, and a second form was created by reversing the order of the items. For each item, participants responded to the same likelihood judgment question as in Experiments 2 and 3.
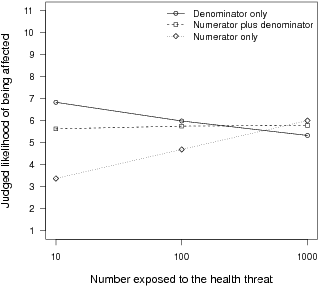
Figure 7: The mean intuitive likelihood judgment as a function of the number of people exposed to the health threat, separately for the three information conditions. The results are collapsed across the two probabilities and the two health threat scenarios.
Figure 7 presents the mean likelihood judgment as a function of the number of people exposed, separately for each information condition. Consistent with the previous studies, there was no main effect of health threat, F(1,82) = 0.83, p = .36, or of item order, F(1,82) = 0.93, p = .76, but there was a main effect of the objective probability, F(1,82) = 80.33, p < .001. Most strikingly, there was a significant interaction between the number exposed and the information condition, F(2,82) = 36.95, p < .001. There was a group-diffusion effect in the denominator only condition, F(1,28) = 21.37, p < .01, and no effect in the numerator-plus-denominator condition, F(1,28) = 0.41, p = .53 — replicating the previous results in a single experiment. But there was also a ratio bias in the numerator only condition, F (1,26) = 36.71, p < .001. Participants presented with explicit numerator information but no explicit denominator information judged their risk to be greater as the number of people exposed (and therefore the number expected to be affected) increased.
In the present studies, we replicated Yamaguchi’s (1998) group-diffusion effect on people’s intuitive likelihood judgments for health threat scenarios and extended it to lottery scenarios. People judged the likelihood of the various outcomes to be lower as the number of people exposed to the threat or involved in the lottery increased. In addition, we showed that explicitly presenting the number of people expected to be affected or selected (the numerator) in addition to the number exposed to the threat or playing the lottery (the denominator) eliminates the effect, and that explicitly presenting the numerator but not the denominator reverses the effect. This entire pattern of results seems inconsistent with Yamaguchi’s (1998) suggestion that the group-diffusion effect is the result of people’s using an interdependence heuristic and perceiving an illusory safety in numbers.
Instead, it is consistent with the idea that information can be presented so that participants attend to and weight either the denominator or the numerator more heavily in their likelihood judgments. Thus, this research dovetails nicely with research on the ratio bias (e.g., Denes-Raj & Epstein, 1994; Yamagishi, 1997). Our contention is that the primary difference between situations in which the group-diffusion effect is observed and situations in which the ratio bias is observed is the amount of attention drawn to the denominator versus the numerator of the relevant ratio. The group-diffusion effect is more likely to be observed when the denominator is more salient and the ratio bias is more likely to be observed when the numerator is more salient. This is consistent with the ideas of Reyna and Brainerd (2008), that the ratio bias occurs in part because reasoning about situations in which the members of a smaller category (e.g., people expected to be affected by the threat) are included in a larger category (e.g., people exposed to the threat) is inherently difficult. This inherent difficulty, combined with easily remembered or processed numerator information, is what produces the ratio bias. In essence, we are adding the idea that problems can also be structured so that the denominator is more easily remembered or processed, in which case there is a group-diffusion effect.
It is clear, though, that we still need a comprehensive theory that specifies all the conditions under which people are more sensitive to the denominator than the numerator of the relevant ratio and therefore allows us to predict when people will exhibit a group-diffusion effect, a ratio bias, or even a null effect. Consider, for example, that our Experiment 3 produced neither a ratio bias nor a group-diffusion effect. But previous research that explicitly presented both the numerator and the denominator produced ratio biases (Bonner & Newell, 2008; Yamagishi, 1997). One reason for this might be that there were additional factors that caused people in those previous studies to attend to and weight the numerator more than the denominator. In the case of Yamagishi’s study, this could be the fact that his questionnaire listed the number of people expected to die from each cause separately, but it presented the size of the reference class (e.g., 100 vs. 10,000) only once in the instructions at the beginning. By the time participants started in on their task, they may not have been thinking about the size of the reference class anymore. In the case of Bonner and Newell’s study, it could be that the verbal expressions every day versus ever year do not adequately communicate the quantitative fact that the latter is 365 times greater than the former, which prevents that manipulation from having much impact on people’s risk judgments.
Other factors are likely to influence the relative salience of the denominator and numerator as well. For example, in much of the research on ratio bias, participants choose between two lotteries described in terms of numerators and denominators. Under such conditions, numerators might have an especially large effect on people’s choices because they are generally easier to compare than denominators (Denes-Raj & Epstein, 1994). When people make intuitive likelihood judgments about individual lotteries, group-diffusion effects might be much easier to observe. Another factor is imaginability, which has been implicated as a cause of the ratio bias and similar effects (Koehler & Macchi, 2004; Newell, Mitchell, & Hayes, 2008). For example, Slovic, Monahan, and MacGregor (2000) found that a psychiatric patient was perceived as more dangerous when it was reported that 20 in 100 similar patients will commit a violent act than when it was reported that there is a 20% chance that the patient will commit a violent act. They argued that the “20 in 100” phrasing is more likely to bring to mind images of violent acts being committed. But perhaps denominators can be made more imaginable too. In fact, this might be part of the reason that we observed the group-diffusion effect here. We began each item by asking people explicitly to imagine the number of people exposed: “Imagine that you are one of N people….”
The development of a more comprehensive theory is important for the practical domain of risk communication. It is likely that there are many factors that effect the relative salience of the number of people exposed to a risk relative to the number expected to be affected. Creating the most effective methods of risk communication will require that we understand what they are.
Chua, H. F., Yamaguchi, S., & Yates, J. F. (2001, November). Explaining the risk diffusion effect: The illusion of safety in numbers. Poster presentation at the annual meeting of the Society for Judgment and Decision Making, Orlando, FL.
Dale, D., Rudski, J., Schwarz, A., & Smith, E. (2007). Innumeracy and incentives: A ratio bias experiment. Judgment and Decision Making, 2, 243–250.
Denes-Raj, V., & Epstein, S. (1994). Conflict between intuitive and rational processing: When people behave against their better judgment. Journal of Personality and Social Psychology, 66, 819–829.
Denes-Raj, V., Epstein, S., & Cole, J. (1995). The generality of the ratio bias phenomenon. Personality and Social Psychology Bulletin, 21, 1083–1092.
Gigerenzer, G. (1994). Why the distinction between single-event probabilities and frequencies is important for psychology (and vice versa). In G. Wright and P. Ayton (Eds.), Subjective probability (pp. 129–161). Chichester: Wiley.
Ho, A., & Leung, K. (1998). Group size effects on risk perception: A test of several hypotheses. Asian Journal of Social Psychology, 1, 133–145.
Koehler, J. J., & Macchi, L. (2004). Thinking about low-probability events: An exemplar-cuing theory. Psychological Science, 15, 540–546.
Newell, B. R., Mitchell, C. J., & Hayes, B. K. (2008). Getting scarred and winning lotteries: Effects of exemplar cuing and statistical format on imagining low-probability events. Journal of Behavioral Decision Making, 21, 317–335.
Piaget, J., & Inhelder, B. (1975). The origin of the idea of chance in children. New York: Norton (originally published 1951).
Pinto-Prades, J.-L., Martinez-Perez, J.-E., & Abellán-Perpiñán, J.-M. (2006). The influence of the ratio bias phenomenon on the elicitation of health states utilities. Judgment and Decision Making, 1, 118–133.
Reyna, V. F., & Brainerd, C. J. (2008). Numeracy, ratio bias, and denominator neglect in judgments of risk and probability. Learning and Individual Differences, 18, 89–107.
Slovic, P., Monahan, J., & MacGregor, D. G. (2000). Violence risk assessment and risk communication: The effects of using actual cases, providing instructions, and employing probability vs. frequency formats. Law and Human Behavior, 24, 271–296.
Stone, E. R., Sieck, W. R., Bull, B. E., Yates, J. F., Parks, S. C., & Rush, C. J. (2003). Foreground:background salience: Explaining the effects of graphical displays on risk avoidance. Organizational Behavior and Human Decision Processes, 90, 19–36.
Stone, E. R., Yates, J. F., & Parker, A. M. (1997). Effects of numerical and graphical displays on professed risk-taking behavior. Journal of Experimental Psychology: Applied, 3, 243–256.
Triandis, H., & Trafimow, D. (2001). Cross-national prevalence of collectivism. In C. Sedikides & M. Brewer (Eds.), Individual self, relational self, collective self (pp. 259–276). New York: Psychology Press.
vos Savant, M. (2006, December). Ask Marilyn. Parade Magazine, p. 9.
Windschitl, P. W., & Krizan, Z. (2005). Contingent approaches to making likelihood judgments about polychotomous cases: The influence of task factors. Journal of Behavioral Decision Making, 18, 281–303.
Yamagishi, K. (1997). When a 12.86% mortality is more dangerous than 24.14%: Implications for risk communication. Applied Cognitive Psychology, 11, 495–506.
Yamaguchi, S. (1998). Biased risk perceptions among Japanese: Illusion of interdependence among risk companions. Asian Journal of Social Psychology, 1, 117–131.
Yamaguchi, S., Gelfand, M., Ohashi, M., & Zemba, Y. (2005). The cultural psychology of control: Illusions of personal versus collective control in the United States and Japan. Journal of Cross-Cultural Psychology, 36, 750–761.
Yamaguchi, S., Okumura, T., Chua, H. F., Morio, H., & Yates, J. F. (2008). Levels of control across cultures: Conceptual and empirical analysis (pp. 123–144). In F. J. R. van de Vijver, D. A. van Hemert, & Y. H. Poortinga (Eds.), Multilevel analysis of individuals and cultures. New York: Erlbaum.
This document was translated from LATEX by HEVEA.