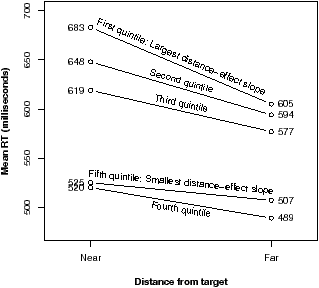
| Figure 1: Quintile split on the distance-effect slope across younger and older adults (n = 29/quintile). |
Judgment and Decision Making, vol. 3, no. 8, December 2008, pp. 619-635
Intuitive numbers guide decisionsEllen Peters* 1,2, Paul
Slovic1,2, Daniel Västfjäll1, and C. K. Mertz1 |
Measuring reaction times to number comparisons is thought to reveal a processing stage in elementary numerical cognition linked to internal, imprecise representations of number magnitudes. These intuitive representations of the mental number line have been demonstrated across species and human development but have been little explored in decision making. This paper develops and tests hypotheses about the influence of such evolutionarily ancient, intuitive numbers on human decisions. We demonstrate that individuals with more precise mental-number-line representations are higher in numeracy (number skills) consistent with previous research with children. Individuals with more precise representations (compared to those with less precise representations) also were more likely to choose larger, later amounts over smaller, immediate amounts, particularly with a larger proportional difference between the two monetary outcomes. In addition, they were more likely to choose an option with a larger proportional but smaller absolute difference compared to those with less precise representations. These results are consistent with intuitive number representations underlying: a) perceived differences between numbers, b) the extent to which proportional differences are weighed in decisions, and, ultimately, c) the valuation of decision options. Human decision processes involving numbers important to health and financial matters may be rooted in elementary, biological processes shared with other species.
Keywords: decision making, numerical cognition, numeracy, proportional
reasoning, individual differences.
Intuitive representations of the mental number line are defined as nonverbal representations of numerosity that are spontaneously activated in the presence of numeric information regardless of format (e.g., • • • •, 4, four; Dehaene, 1996). The representations are “inner marks” that allow verbal and nonverbal animals to “think unnamed numbers” (Koehler, 1950, cited in Gallistel, 1990). Trained monkeys, for example, can order objects 1–9 by their numerosity (Brannon & Terrace, 1998). Adult humans can perform arithmetic operations quickly on larger arrays of dots using these nonverbal mental magnitudes (Barth et al., 2006).
The number domain is a prime example where strong evidence points to a biologically determined, domain-specific representation of number and elementary arithmetic operations linked to the inferior parietal cortex, specifically the horizontal intra-parietal sulcus in both adults and children (Cantlon et al., 2006; Dehaene et al., 2003; Pinel et al., 2001, 2004). Arabic, spelled-out, and spoken numerals all activate this area so that it is thought to be involved in cross-modal, abstract representation and manipulation of the quantity meaning of numbers, rather than being activated by any specific number notation (Piazza et al., 2004). Numerical-cognition researchers believe that this basic numerical intuition lays the foundation for uniquely human mathematical reasoning (Wilson et al., 2006; Halberda et al., 2008).
Number intuitions, however, are limited in their representational power and do not directly support concepts of fractions, probabilities, or even the precise numbers important to many decisions. Although little research exists, processing these more sophisticated concepts is thought to be based nonetheless on humans’ basic “number sense” with brain areas originally developed for other purposes co-opted for nonintuitive, symbolic number processing. The goal of this paper is to develop and test hypotheses about the influence of such evolutionarily ancient, intuitive numbers on human decisions.
Numerical information is ubiquitous in the decisions that guide our lives, and it is generally assumed that if provided appropriate numbers, people will be numerate1 enough to understand and use them as intended. Less numerate individuals, however, fare less well in important medical and financial decisions involving numeric information (Estrada et al., 2004; Banks & Oldfield, 2007; Peters et al., 2006). The present research represents, to our knowledge, the first attempt to explore whether an evolutionarily ancient number-processing mechanism might influence adult numeracy as well as choices involving numeric information.
Table 1: The subjective difference between two numbers based on different logarithmic bases for mapping
numbers =
Number discrimination in human and non-human animals conforms at least qualitatively to Weber’s law such that the greater the reference numerosity, the more imprecisely human and non-human animals distinguish between it and nearby numerosities, causing confusions between nearby numbers — a distance effect. In their pioneering studies of the symbolic distance effect (symbolic numerals are numerosities conveyed with numeral symbols such as Arabic integers or spelled-out number words), Moyer and Landauer (1967) asked subjects to judge the numerical order of Arabic numerals as rapidly as possible (Is 2 greater than or less than 4?). Performance was determined by the relative numerical distance; the greater the distance between two numbers, the more quickly their order was judged and the fewer errors were made. Subjects are faster and more accurate in comparisons of 5 and 9 than they are in comparisons of 5 and 6. A size effect was subsequently found by Parkman (1971) such that the greater the numerical value of the smaller digit, the longer it took to judge their order, holding constant the difference between the numbers. As per Weber’s law, the discriminability of two magnitudes (whether symbolic or non symbolic) is a function of their ratio rather than their absolute difference (Dehaene, 1997). The symbolic distance effect and size effect are observed at least in the single- and double-digit ranges (e.g., Dehaene et al., 1990, but see Link, 1990). The distance effect represents the discriminability of magnitudes and the precision with which the mental number line is represented. It is measured as the slope or difference of the reaction times (RTs) when comparing numbers that are close together versus far apart. A smaller slope indicates greater numerical precision in the representations of the numbers being compared.
Moyer and Landauer’s (1967) notion of a perceptual comparator that explains the distance effect is shared by the bulk of the models of numerical cognition that differ in other respects (see Algom et al., 1996; Dehaene, 1996; Gallistel & Gelman, 2005; Link, 1990). In it, a perceived numerosity (greater than about three) is represented by a Gaussian-like distribution of activated numerosities. Each distribution has a fixed width and distributions of two numbers being compared will overlap more with smaller distances between two numbers and as numbers get larger, thus increasing reaction times (RTs) and errors in number-comparison tasks and explaining the distance effect.
Although competing mathematical formulations of the precision of mental-number-line representations exist (Dehaene & Changeux, 1993; Gallistel & Gelman, 2005), they make similar behavioral predictions in number-comparison studies and (we believe) in decision making. To begin with, more precise representations may be associated with numeracy skills linked with decision making in previous studies (Peters et al., 2006; Peters, Hibbard, et al., 2007). In support of this notion, children with more precise representations show better math ability compared to children with less precise representations (Halberda et al., 2008). This finding may be due to children with more precise representations discriminating numbers more easily and developing better math abilities as a result or because differences in the quantity or quality of engagement in formal mathematics might increase the precision of representations (or to some third factor that affects both measures). In the present paper we measure the precision of mental-number-line representations and test whether numeracy scores among college students were associated with the precision of their representations.
Hypothesis 1: Individuals with more precise representations will be higher in numeracy than those with less precise representations.
In decision making, individuals with more precise representations should also discriminate between two numbers better and perceive the numbers to be further apart than those with less precise representations. Numeric differences between options that are perceived as larger should result in a greater difference in the perceived values of the two options.
Human decision making likely derives in part from the same mechanisms evolved by other animals in response to risky natural environments (Weber et al., 2004). To the extent that intuitive rather than deliberative processing mediates human decision making, humans and animals should demonstrate similarities in choice processes. Animals spontaneously use numerosity based on ratios to make decisions (Meck & Church, 1983). Hauser et al. (2003), for example, found that untrained cotton-top tamarind monkeys oriented their heads towards a speaker more often when a novel number of syllables were spoken; “novelty” was indexed by the ratio between two numerosities independent of their absolute value.
We hypothesized that individuals with smaller distance-effect slopes (more precise representations) would perceive greater differences between two numbers compared to individuals with larger slopes and that this perception would, in turn, guide valuation processes underlying choice. The curve that relates numerical distance to reaction time is approximated by a logarithmic function (e.g., Dehaene, 1989).2 We hypothesized, therefore, that individual differences in the precision of mental-number-line representations would be due to individuals having different bases for the logarithmic function that converts symbolic numbers to perceived numbers. Logarithmic transformations of numbers have useful properties that can be applied to understanding the possible effects of individual differences in the precision of mental-number-line representations on the valuation of numeric differences.
To begin with, a logarithmic transformation means that the perceptual difference between two numbers will depend on their proportional difference and not their subtractive difference. For example, imagine that Person A’s representation depends on a natural-log (base e) transformation. A proportional difference of two (100 compared to 50 or 10 compared to 5) would engender a perceived difference of .693 (ln(2x)-ln(x) = .693 for all x; Table 1). The subjective difference between 100 and 50 would then be the same as that between 800 and 400 or 12 and 6. Barring any influence from other processes, this means that an individual who preferred a 60% chance to win $100 over a certain $50 will also tend to prefer a 60% chance to win $800 over $400 and 60% to win $12 over $6.
Second, Person A will always perceive a greater difference between two numbers compared to Person B who has a larger base for the logarithmic transformation. For example, imagine that Person B demonstrates a larger distance-effect slope than Person A and his representation uses a log10 transformation (compared to A’s natural-log transformation). In this case, with a proportional difference of two, B would perceive a difference of .301 (log10(2x)-log10(x) = .301 for all x) whereas A would perceive a difference of .693 (ln(2x)-ln(x) = .693 for all x). Thus, Person A would perceive a bigger difference than B on the subjective number scale.
Hypothesis 2: Individuals with more precise representations of the mental number line will make choices consistent with valuing the same proportional difference more than individuals with less precise representations.
We test this hypothesis in Study 1’s intertemporal choices between immediate, smaller rewards and later, larger rewards as well as in Study 2’s choice between options that offer larger absolute differences but smaller proportional differences and an option that offers a smaller absolute difference but larger proportional difference.
The extent of the difference in preferences among those with more and less precise representations, however, should depend on the extent of the proportional difference between two numbers in a choice. Specifically, perceptual differences between individuals who vary in the precision of their mental-number-line representations will be greater with larger proportional differences between two numbers. With a larger compared to a smaller proportional difference, Person A would perceive an even greater difference than Person B. For example, a proportional difference of five would engender perceived differences of 1.609 and .699 for Person A and Person B, respectively (see Table 1), suggesting that both individuals would value five times more of X more than they would twice more of X, but Person A would find it even more attractive than Person B.
Hypothesis 3: Individuals with greater precision will weigh proportional differences among numeric attributes even more in choice than those with less precise representations when larger compared to smaller proportional differences exist between numeric attributes.
We test this hypothesis in Study 1 with two intertemporal choices (a choice between an immediate, smaller reward and a delayed, larger reward) that differ in the extent of the proportional difference between the two monetary rewards.
Given indication of the existence of individual differences in the precision of mental-number-line representations and their link with higher order number skills in children (Halberda et al., 2008), the overarching aim of this paper is to measure individual differences in precision using a distance-effect paradigm and then to relate this measure to performance in two decision tasks. The decision tasks we chose are quite different on the surface but contain elements of number comparisons (absolute versus proportional differences) that should relate to the precision of mental-number-line representations. Because such representations have been associated with number skills in children, we also test this relation in an adult sample. Subsequently, we test for the effects of these representations on decisions with and without controlling for numeracy and age. For simplicity, the distance-effect task and two decision tasks are presented as three separate studies, but all three tasks were conducted with the same group of subjects.
Table 2: Sample characteristics in the younger and older age groups.
Characteristic (N = 80)
(N = 65)
Inferential test for difference between two age groups Mean age t(87.7) = –64.7a**** Age range % female χ2 (df = 1) = .24 Speed of processing t(142) = 12.0**** Working memory t(120) = 3.8a*** Vocabulary t(143) = –8.1**** Numeracy t(143) = 3.6*** Education t(76.8) = –4.3a**** Health t(140) = 2.9** a Due to unequal variances, a Satterthwaite approximation was used to calculate df and t-values. *p < .05. **p < .01. ***p < .001. ****p < .0001.
Younger and older subjects were recruited in order to examine the generalizability of effects at the two ends of the adult continuum. Some evidence also suggests that older adults may rely more than younger adults on automatic mechanisms, such as mental-number-line representations, rather than controlled processes in judgment and decision processes (Peters, Hess, et al., 2007).
Initially-recruited subjects included 83 younger adults from the University of Oregon who received course credit for participation and 79 older adults from local senior centers who were paid $20 each for their participation (an additional $5 each was donated to their senior center).
Subjects first completed a number-comparison (distance-effect) study conducted on a computer, and then responded to the two decision tasks3, measures of numeracy (Lipkus et al., 2001; see Appendix A for items), fluid intelligence, and crystallized intelligence and responded to some demographic questions. For fluid intelligence, the WAIS III Letter-Number Sequencing and digit-symbol substitution tasks (Wechsler, 1997) were used to assess working memory functioning and processing speed, respectively. Higher scores on each task mean better working memory and faster speed of processing, respectively. For crystallized intelligence, subjects completed Vocabulary Test II (parts 1 and 2) from the Kit of Factor-Referenced Tests (Ekstrom et al., 1976).
We conducted two distance-effect tasks modeled on prior research (Dehaene, 1996; Temple & Posner, 1998). In each task, a quantity was shown in the middle of the computer screen and subjects responded whether the quantity shown was bigger or smaller than a target quantity (e.g., Is 4 bigger or smaller than 5?). After responding to a given quantity, that quantity would disappear and the next quantity would appear. No feedback about accuracy was provided. The target quantity was held constant in each block. Reaction time (RT) and accuracy were recorded for each response. Half of the subjects responded “larger” with the right hand and “smaller” with the left; for the other half of the subjects, this was reversed. Half of the subjects in each hand condition completed a Standard task (described below) first followed immediately by a Modified task; order was reversed for the other half of the subjects.
In the Standard distance-effect task with single-digit numerosities, subjects were presented with one of four Arabic integers 1, 4, 6, and 9 in one block and corresponding arrays of dots in another block and were asked to press one of two large buttons to indicate as quickly and accurately as possible whether the quantity shown was larger or smaller than “5”. The Arabic integers were displayed at 2 cm height. The dots were displayed in a 5x5 cm square, one dot taking up the whole square and more dots condensed to fit that space. Half of the quantities shown were close to the target 5 (4 and 6); the other half were numerically farther from the target 5 (1 and 9). Subjects were shown two blocks per notation type with 8 practice trials and 80 experimental trials per block. Block order was counterbalanced across subjects.
A Modified distance-effect task, using numbers between 0 and 1 that are often important in decision making, was also conducted. The procedure was similar to the standard task except that subjects were presented with quantities corresponding to 10%, 25%, 40%, 60%, 75%, and 90% in three notation types (decimals, e.g., “.10”, frequencies, e.g., “10 out of 100”, and percentages, e.g., “10%”) and were asked to indicate as quickly and accurately as possible whether the quantity shown was bigger or smaller than the target “50%.” The quantities represented three distances from 50%: near, middle, and far. The middle quantity was included only to make the Standard and Modified task appear more different. The stimuli were 2 cm high and varied in width. The width of “X out of 100” was the longest, at approximately 12 cm in length. Subjects responded to six blocks (two per notation type) with 12 practice trials and 120 experimental trials per block.
Three younger adults and fourteen older adults were excluded from analyses due to computer problems, loud noises during the computer task, or inattention to the task, for a total of 145 subjects (80 younger adults and 65 older adults) used in the analyses. The two age groups included similar proportions of female subjects. Younger adults scored higher than their older counterparts on measures of processing speed, working memory, and numeracy, and scored lower on vocabulary. Younger adults reported fewer years of education and better health. See Table 2.
We first report reaction-time and error results from the distance-effect tasks and analyze their relation with numeracy. Using a hierarchical linear modeling approach, we estimate the distance effect shown by each subject across notations and subsequently use this measure of the precision of mental-number-line representations to test hypotheses in two decision tasks.
Data from the standard and the modified distance-effect tasks were combined. However, to have comparable data from both tasks, we deleted all RTs associated with the mid-distance on the modified task (analyses of the modified task were similar with and without these middle values). RTs that were judged as too fast and indicative of inattention were deleted.4 RTs over 3 standard deviations from the subject’s mean (after standardizing within the Standard and Modified tasks) were also treated as missing (Ratcliff, 1993) (total = 4.1% missing data). The proportion of errors was low (mean errors = 1.9%; range = 0–8.9%).
Then, for each subject, the average unstandardized RT for each notation type, distance (near and far) and magnitude was computed first across all RTs for correct and incorrect trials. The 20 average RTs per subject (5 notations x 2 distances x 2 bigger/smaller than target) were then entered into a random-effects model using SAS PROC MIXED.5,6 All subjects had complete data. Predictors of these average RTs were age group (coded –1 for younger adults and +1 for older adults) and numeracy (a continuous variable and mean-deviated) at Level 2 and distance (coded as –1 for near and +1 for far), and notation (entered as a categorical variable) at Level 1. The model also included five two-way interactions (age group with notation and distance, notation with distance, numeracy with age group and distance) and the three-way interaction of numeracy, age group, and distance). In a separate analysis, the number of errors made by each subject was entered at Level 2 to test for between-subjects speed-accuracy tradeoffs and was entered at Level 1 for each subject in each of the 20 cells to test for within-subjects speed-accuracy tradeoffs. Subjects who were faster overall (the between-subjects effect) made significantly more errors in this task, F(1,141)=21.03, p<.001. However, inclusion of the number of errors at Level 1 and Level 2 did not substantially change the effect of distance or its interaction with numeracy.7 Because no such tradeoff (bias) was evident within subjects, F(1, 2368) = .98, p = .32, and previous research was based on RTs to correct trials only, we present analyses based on mean RTs to correct trials only throughout the rest of the paper. Analyses of RTs and of the relation of individual differences in the distance effect with performance in the decision tasks were similar, however, with and without inclusion of incorrect trials. The relation of these individual differences to numeracy and to decision performance was also similar when the individual differences were re-estimated from a weighted average of the distance effect based on RTs and on errors.
The model results corroborated previous findings and demonstrated a significant interaction between the distance effect and numeracy such that individuals higher in numeracy showed smaller distance effects (i.e., more precise representations of the mental number line). Because the focus of the present paper is on the relation of the distance-effect slope with decision making and not on the distance effect itself, full results of the model can been found in Appendix B.
Smaller slopes (less of an RT change between near and far comparisons; see Figure 1) indicate greater precision of representations of the mental number line. The difference from the smallest to the largest distance effect was about 1/10 of one second (mean of the average RT for far comparisons minus the average RT for near comparisons = –45 msec, range = –115 to +9 msec). We examined the reliability of the measure first by examining the correlations between mean RT differences for number comparisons that were near versus far among the five notations. The distance effect appears to be a reliable individual-difference construct across notations (Cronbach’s alpha = .76).

Figure 1: Quintile split on the distance-effect slope across younger and older adults (n = 29/quintile).
To examine individual differences, the random-effects model was used to approximate each subject’s distance-effect slope (which represents the degree to which numbers near versus far from a target can be discriminated from the target and thus represents the precision of mental numbers) by modeling each subject’s average RT to near and far magnitudes separately for each notation. For each individual, the near RT was subtracted from the far RT by notation and then averaged across all notations and divided by a constant of one to produce the “slope” variable. This choice of denominator allows us to interpret results in the decision tasks based on millisecond changes in the size of the distance effect. Since the resulting slope variable was significantly skewed, one outlier was winsorized from –103 to –90.5. The reliability of the distance-effect measure was calculated for each individual and then averaged across individuals (average reliability, λ, of the ordinary least squares estimator as a measure of the distance-effect slope = .72; Raudenbush & Bryk, 2002). Consistent with Hypothesis 1, smaller distance-effect slopes were moderately correlated with higher numeracy (r = .29, p < .0018). See Appendix B for further discussion of this relation. Hypothesis 1 was supported.
If multiple sources of information exist in a decision (even if it is multiple transformations of given numbers), then individuals who represent the mental number line more precisely should perceive a proportional difference between two numbers as greater than those who have less precise representations, and they should weigh it more in decisions.9 Thus, we predict that the proportional difference between magnitudes of an immediate and a delayed reward (rather than their simple subtractive difference) will matter more for individuals with smaller distance-effect slopes compared to those with larger slopes (Hypothesis 2). In addition, the extent of the perceived difference between two monetary rewards for those with smaller slopes compared to larger slopes will be larger with larger proportional differences between the monetary rewards (Hypothesis 3). As a result, the distance-effect slope should be a better predictor of intertemporal choices when the proportional difference between the rewards is larger (compared to smaller) even if the subtractive difference between the rewards is smaller.10
Subjects (N = 129; 64 were younger adults) responded to two hypothetical intertemporal choices. One choice had a small proportion difference between the monetary rewards offered, but a larger subtractive difference ($100 now or $110 in a month). The second choice ($10 now or $15 in a week) had a larger proportional difference and a smaller subtractive difference (it also offered a greater implied rate of return). Subjects responded to both problems on a 12-point preference scale ranging from –6 = much prefer [the smaller reward] now to +6 = much prefer [the larger reward] later; no zero-point was included.
If we ignore time-delay differences and treat dollar differences simply as symbolic numbers, then smaller slopes, which indicate more precision, should lead to a greater perceived difference between the two monetary rewards, particularly when a larger proportional difference exists such as in the $10/$15 choice. This means that individuals with smaller slopes should be particularly likely to choose the delayed rewards in this choice. Going back to our initial example for illustration, Person A with the natural-log transformation would perceive a difference between 100 and 110 of .095 whereas Person B (log10 transformation) would perceive a .041 difference. Log transformations of 10 versus 15 ( the second choice) demonstrate a greater difference in perceived number between Persons A and B (.405 for Person A and .176 for Person B). Thus, we predict a greater association of the slope (due to proportional differences) independent of numeracy with preferences in the $10/$15 choice as compared to the $100/$110 choice.
Subjects tended to prefer the smaller, immediate reward in the $100/$110 choice (mean preference = –1.4; SD = 4.7) and the larger, later reward in the $10/$15 choice (mean preference = 1.8; SD = 4.3). Individuals who delayed reward in one choice also tended to delay reward in the other choice (r = .51, p < .001). Simple correlations of the distance-effect slope with choices provided preliminary support for Hypothesis 3; in the $10/$15 choice (with the greater proportional difference), individuals with smaller (less negative) distance-effect slopes were more likely to delay rewards; no such relation existed in the $100/$110 choice (r = .18, p < .05, and –.03, ns, respectively, in the $10/$15 and $100/$110 choices). A test of these two dependent correlations indicated that they were significantly different, supporting Hypothesis 3 that responses will be associated with the distance-effect slope and more so for larger than smaller proportional differences between outcomes, T2(126) = –2.4, p = .0211 (Steiger, 1980).
Table 3: Intertemporal choice — General-linear-model results of the scaled preference (–6=much prefer immediate reward to +6=much prefer delayed reward) by the distance-effect slope, age, numeracy, and gender.
F(10, 115) = 1.2,
ns, R2 = .09
F(10,115) = 2.1,
p < .05, R2 = .15
Predictor Intercept Age Numeracy Slope Age*Numeracy Age*Slope Numeracy*Slope Age*Numeracy*Slope Gender Gender*Numeracy Gender*Slope †p < .10. *p < .05. **p < .01. ***p < .001.
We also controlled for age and numeracy in analyses of the effects of the precision of mental-number-line representations (measured by the distance-effect slope) on decisions for statistical reasons12 and because previous aging literature suggests the potential for differential effects of numeracy and the distance-effect slope on choices of younger and older adults. In Study 1, we tested two general linear models to examine the effect of the distance-effect slope separately on each choice controlling for numeracy and age (all variables are mean-deviated) and test whether the slope predicted choices over and above the influence of age and numeracy. The 2- and 3-way interactions of age with numeracy and slope were added to test the hypothesis that the decisions of older adults might reflect more automatic processes such as the distance effect than controlled processes such as numeracy compared to younger adults (Peters, Hess, et al., 2007). Gender and its interactions with numeracy and slope were also included because Frederick (2005) found gender differences in the influence of numeracy on intertemporal choices. Age group and gender were treated as categorical variables and slope and numeracy were treated as continuous.
For the $100/$110 decision, no variable attained conventional significance after controlling for all other predictors (see Table 3 for inferential statistics).
For the $10/$15 decision, individuals with smaller distance-effect slopes delayed reward significantly more often (means = 2.5 and 1.2, respectively, for those with smaller and larger slopes based on a median split of the slope). Examination of parameter estimates in Table 3 indicates that, for every one millisecond decrease in the size of the distance effect, preferences for $15 in a week (over $10 now) increased by .08 units on the preference scale. Individuals with smaller distance-effect slopes delayed reward significantly more often only in the $10/$15 choice. Hypothesis 2 (that individuals with more precise representations will value the same proportional difference more than individuals with less precise representations, regardless of the size of the proportional difference) received only partial support since the effect of slope on the $100/$110 choice was not significant. Hypothesis 3, which posited a larger effect of the slope in choices with larger compared to smaller proportional differences, was supported. Predicted preferences (shown in Figure 2) illustrate this effect controlling for all other factors13.
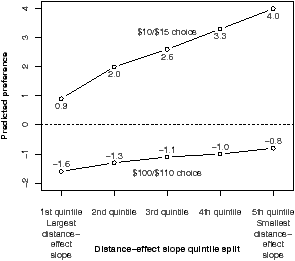
Figure 2: Study 1. Predicted preference by slope quintile split (–6 = prefer immediate reward to +6 = prefer delayed reward).
Thus, the precision of the mental number line appears to influence choices and to influence them more when a larger proportional difference existed between two options, as indicated by the significant difference in dependent correlations.
Are the effects due to general intelligence? Controlling for individual differences in continuous measures of working memory, speed of processing, and vocabulary in the analyses of the two choices in Table 3 revealed little difference in the influence of the slope on choices between $100 and $110 (the coefficient for the slope was .021, p = .60 in Table 3 and .031, p = .45 after controlling for the three measures) or between $10 and $15 (the coefficient for the slope was .076, p = .03 in Table 3 and .071, p = .05 after controlling for the three measures). Simple correlations of the slope with the $100/$110 and $10/$15 choices were r = –.03 and .18, respectively, without the three measures and .01 and .18, respectively, with them. Intelligence, as assessed by these proxy measures, does not explain the effects of the precision of mental-number-line representations on these intertemporal choices.
The influence of the distance-effect slope on intertemporal choices suggests the possibility of a stable component of discount factors that could be modeled (Soman et al., 2005). Like Soman et al., we also suggest a nonlinear effect in such choices. However, while they discuss a nonlinearity for outcomes due to time (immediate rewards are processed differently than delayed rewards; see also McClure et al., 2004), we argue for a nonlinearity independent of their proposed effect based on the proportional difference in the two monetary outcomes.
A limitation of this study is that we did not equate overall preferences or time delay across the two choices. It is possible that the precision of mental-number-line representations may have been associated with choices, not only because of a proportional difference in the monetary outcomes but also because precision could be associated with sensitivity to timing processes as well (Meck & Church, 1983).14 In Study 2, we examine the relation of precision in a choice that pits proportional differences against absolute differences in the absence of any timing differences.
We next employed a task designed by Fetherstonhaugh et al. (1997) to discriminate the influence of proportional reasoning from subtractive differences in choices, when subtractive differences are normatively relevant.
In the task, subjects (N=120; 60 were younger adults15) were told to imagine that they distributed money for a charitable foundation to institutions that develop treatments for serious diseases. In the current choice, they were to select one proposal to fund (awarding $10 million) from three submitted proposals. Institution X proposed to treat a disease and reduce deaths from approximately 15,000/year to about 5,000/year, Institution Y would reduce deaths from approximately 160,000/year to 145,000/year, and Institution Z would reduce deaths from approximately 290,000/year to 270,000/year. Note that a choice of Institution Z saves the greatest number of lives (about 20,000) but the smallest proportion of lives (6.9%) whereas Institution X saves the fewest number of lives (about 5,000) but the greatest proportion (67%).
We expected that individuals with more precise mental-number-line representations (smaller distance-effect slopes) would perceive the differences in proportions as greater and, as a result, would be more likely than other subjects to choose Institution X, the option that saved the greatest proportion of lives (but fewest number of lives). Greater numeracy, on the other hand, might be expected to relate to choosing Institution Z to save the greatest absolute number of lives as it has been associated with a greater weighting of absolute numeric differences in choice (Peters et al., 2006).
Examination of the simple effect of the distance-effect slope revealed a non significant trend in the expected direction (43% and 26% of those with smaller and larger slopes, respectively, chose X). As in Study 1, we next analyzed the choice results controlling for age, numeracy, and their interactions with the slope.
As hypothesized, individuals with smaller distance-effect slopes appeared to value the larger proportional difference more; they chose Institution X (which saved a smaller number of lives but a greater proportion of lives) more often than those with larger distance effects (see Table 4 for inferential statistics based on logistic regression16 and Figure 3 for predicted choices based on the slope on average across age and numeracy and after controlling for the interactions). Neither numeracy nor its interaction with the distance-effect slope was significantly related to performance in the logistic regression.17 Thus, contrary to the hypothesis that the effects of numeracy and the distance-effect slope would be dissociable, higher numeracy was not associated with a greater weighing of absolute differences (although smaller slopes were associated with a greater weighing of the larger proportional difference after controlling for numeracy). The possible differential effects of the precision of mental-number-line representations and numeracy deserve further study.
Table 4: Logistic-regression results of Institution-X choices in the charitable-foundation task.
Predictor Estimate (df = 1) Wald χ2 Intercept –.61 7.31** Age .50 4.96* Numeracy .11 0.63 Slope .04 3.85* Age*Numeracy .04 0.10 Age*Slope –.003 0.03 Numeracy*Slope –.003 0.08 Age*Numeracy*Slope .02 2.77† †p < .10. *p < .05. **p < .01. ***p < .001.
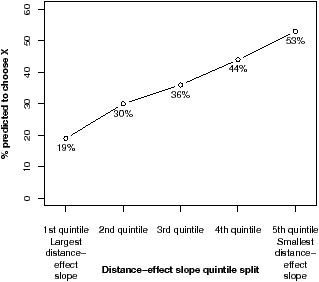
Figure 3: Study 2. Predicted probability of choosing Institution X by distance-effect slope quintile.
Note that the effect of greatest interest here cannot be explained by the simple assumption that those with smaller distance-effect slopes are simply better at everything; here they are more likely to give the normatively incorrect response.
The marginal three-way interaction between age, numeracy, and slope in Table 4 suggests the possible presence of different effects of the precision of mental-number-line representations on choices among younger and older adults. Hypotheses from the cognitive-aging literature suggest that choices of younger adults may be driven more by controlled processes (perhaps such as numeracy) whereas the decisions of older adults may be driven more by automatic processes (perhaps such as the precision of representations; Peters, Hess, et al., 2007). Contrary to this hypothesis, however, it appears from Table 5 that the choices of younger adults and of highly numerate older adults were more consistent with our precision-of-representations hypothesis; in all three comparisons of large to small slope (less numerate younger adults, highly numerate younger adults, and highly numerate older adults), individuals with smaller slopes (more precise representations of the mental number line) chose Institution X more often than those with larger slopes.18
Table 5: Proportion of choices of Institution X among younger and older individuals who vary in the precision of mental-number-line representations (shown as a median split on the distance-effect slope) and numeracy (low scores = 4–8; high scores = 9–11 out of 11 possible)
Younger adults Older adults Less numerate Highly numerate Total
After partialling out the effects of the three proxy intelligence measures, the distance-effect slope was still as predictive of choices; the coefficient for the slope (slope estimate = .04 in Table 4) remained .04 with the addition of the three proxy measures. Individuals with smaller distance-effect slopes appear to value the option with the largest proportional savings of lives (that saved the fewest lives) more than individuals with larger distance-effect slopes.
Previous research has emphasized numeracy as an important factor in health and financial decisions. Results of the present paper suggest that another key concept may be precision of mental-number-line representations that, while modestly related to numeracy, is a separable and measurable construct.
In the present studies, individual differences in this precision, as measured by differences in reaction times, ranged across a mere tenth of a second and appeared to influence numerical reasoning in decisions based on proportional differences. This evolutionarily ancient intuitive sense of numbers was independently associated with choices whereas higher-level numeracy skills were not. Intuitive number representations appear to underlie: a) perceived differences between numbers, b) the extent to which proportional differences are weighed in decisions, and, ultimately, c) the valuation of decision options. The effects remained after controlling for proxy intelligence measures.
To further explore possible effects of individual differences in mental-number-line representations, we plot hypothetical logarithmic mappings from symbolic numbers to perceived numbers in Figure 4 and discuss implications for decision making. As in the Introduction, each line represents an individual, one of whom, Person A, has a smaller logarithmic base for the mapping compared to Person B (A demonstrates a smaller distance-effect slope than B and represents numbers more precisely).
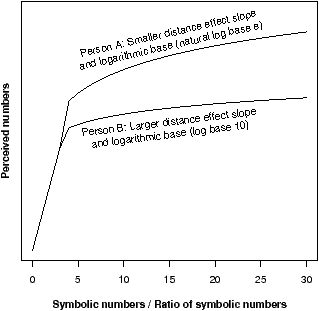
Figure 4: Hypothetical logarithmic mappings from symbolic numbers on the x-axis to subjective (or perceived) numbers on the y-axis. Each line represents a hypothetical individual with a different logarithmic base for the transformation.
Six characteristics of the graph in Figure 4 should be noted. First, an exact linear transformation was used for symbolic numbers 1, 2, and 3 due to a separate process that is not a focus of the present paper (i.e., subitizing; Feigenson et al., 2004). Second, both lines follow Weber’s Law with marginal increases in perceived numbers decreasing with increases in symbolic numbers; this perceptual effect may explain the property of diminishing marginal returns (e.g., Prospect Theory, Kahneman & Tversky, 1979) and suggests the possible existence of a stable component of value that could be modeled across situations at the individual level. As a result and as noted in Hypothesis 2 in the Introduction, the perceptual difference between two numbers (which should influence choices between options) will depend on their proportional difference and not their subtractive difference (see Weber et al., 2004).
Third, an individual with a smaller base for the logarithmic transformation (Person A) will always perceive a greater difference between two numbers than an individual with a larger base (Person B), as illustrated by the line for Person A always being above the line for Person B. Fourth, the difference in perceived numbers between the two individuals expands with increasing symbolic numbers (the lines get further apart at higher numbers as the line for Person B gets flatter than that for Person A at smaller numbers). One implication is that Person B with the larger base will not only perceive numbers less precisely but will demonstrate greater insensitivity to large numbers compared to Person A (e.g., large numbers of human lives; Slovic, 2007; Fetherstonhaugh et al., 1997). Fifth, the x-axis can be used to represent either a symbolic number (such as 10 or a proportional difference between two numbers (such as 10 times more); the figure is accurate for ratios only for ratios greater than 3, however, as we chose to represent 1, 2, and 3 as having exact representations due to subitizing (see the first point above). Finally, and as suggested in Hypothesis, individuals with more precise representations will perceive larger proportional differences as even bigger (compared to those with less precise representations) than smaller proportional differences.
Although not a major focus of the present paper, mean age differences were found in both numeracy and the distance-effect slope when other predictors were not controlled for (see Table 2 and the latter part of Appendix B). One might have expected older adults to rely relatively more than their younger counterparts on intuitive processes such as the distance-effect slope and to rely relatively less on deliberative processes such as that assessed in the numeracy measure (Mather, 2006; Peters, Hess, et al., 2007). This expectation, however, was not supported in our data. Instead, when controlling for other predictors such as numeracy and the distance-effect slope, no age differences were found in the intertemporal choice task, providing some basis for speculation that such factors could underlie, at least in part, observed age differences in decision making. In Study 2, however, older adults were more likely than younger adults to choose the institution that saved the larger proportion but smallest absolute number of lives; in addition, a marginally significant three-way interaction occurred between age, numeracy, and the slope. More targeted future research may discover that we can begin to explain some age differences in decisions involving numeric information through a consideration of numeracy and the precision of mental-number-line representations.
Researchers studying judgment and choice have found that decisions are based on some combination of stable values learned from experience and preferences that are constructed from the decision context (Lichtenstein & Slovic, 2006; Payne et al., 1999). We propose an additional view that intuitive representations of the mental number line also influence valuation across multiple, otherwise unrelated, decision contexts and may provide a stable component of perceived value that can be modeled.
Individuals are increasingly being asked to make decisions about vital life issues in which numbers play a major role. The evolutionarily ancient mechanism described here appears to guide in part such modern-day choices. The present results imply that these mental-number-line representations can potentially support or degrade decision quality. It seems likely that they would most often improve decision quality, however, because more precise representations would allow a decision maker to distinguish better between numeric attributes in choice (e.g., mortgage rates in buying a home, survival rates in choosing a cancer treatment).
More broadly, our proposed framework may lay the foundation for a better understanding of the oft-cited link between greater educational attainment and improved health and wealth (Goesling & Baker, 2008; Goldman & Smith, 2002; Deary, 2008). Greater education may lead to improved intuitions about numbers as well as greater numeracy. These two related, but separable, number skills may lead to improved decision skills in situations that involve an understanding and use of numbers, and ultimately may lead to better choices about health and financial risks (e.g., Bruine de Bruin, Parker, & Fischhoff, 2007). The extent to which formal education influences the learning of lower-level number intuitions, and subsequently guides the development of decision competencies used to make risky health and financial decisions, remains to be tested.
Algom, D., Dekel, A., & Pansky, A. (1996). The perception of number from the separability of the stimulus: The Stroop effect revisited. Memory & Cognition, 24, 557–572.
Banks, J., & Oldfield, Z. (2007). Understanding pensions: Cognitive function, numerical ability and retirement saving. Fiscal Studies, 28, 143–170.
Barth, H., La Mont, K., Lipton, J., Dehaene, S., Kanwisher, N., & Spelke, E. (2006). Non-symbolic arithmetic in adults and young children. Cognition, 98, 199–222.
Brannon, E. M., & Terrace, H. S. (1998). Ordering of the numerosities 1 to 9 by monkeys. Science, 23, 746–749.
Bruine de Bruin, W., Parker, A. M., & Fischhoff, B. (2007). Individual differences in adult decision-making competence. Journal of Personality and Social Psychology, 92, 938–956.
Cantlon, J. F., Brannon, E. M., Carter, E. J., & Pelphrey, K. A. (2006). Functional imaging of numerical processing in adults and four-year-old children. PLoS Biology, 4, e125.
Deary, I. (2008). Why do intelligent people live longer? Nature, 456, 175–176.
Dehaene, S. (1989). The psychophysics of numerical comparison: A reexamination of apparently incompatible data. Perception & Psychophysics, 45, 557–566.
Dehaene, S. (1996). The organization of brain activations in number comparison: Event-related potentials and the additive-factors method. Journal of Cognitive Neuroscience, 1, 47–68.
Dehaene, S. (1997). The number sense: How the mind creates mathematics. New York: Oxford University Press.
Dehaene, S., & Changeux, J.-P. (1993). Development of elementary numerical abilities: A neuronal model. Journal of Cognitive Neuroscience, 5, 390–407.
Dehaene, S., Dupoux, E., & Mehler, J. (1990). Is numerical comparison digital? Analogical and symbolic effects in two-digit number comparison. Journal of Experimental Psychology: Human Perception and Performance, 16, 626–641.
Dehaene, S., Izard, V., Spelke, E. & Pica, P. (2008). Log or linear? Distinct intuitions of the number scale in western and Amazonian indigene cultures. Science, 320, 1217–1220.
Dehaene, S., Piazza, M., Pinel, P., & Cohen, L. (2003). Three parietal circuits for number processing. Cognitive Neuropsychology, 20, 487–506.
Ekstrom, R. B., French, J. W., Harman, H., & Derman, D. (1976). Kit of factor-referenced cognitive tests (rev. ed.). Princeton, NJ: Educational Testing Service.
Estrada, C. A., Martin-Hryniewicz, M., Peek, B. T., Collins, C., & Byrd, J. C. (2004). Literacy and numeracy skills and anticoagulation control. American Journal of the Medical Sciences, 328, 88–93.
Feigenson, L., Dehaene, S., & Spelke, E. (2004). Core systems of number. Trends in Cognitive Sciences, 8, 307–314.
Fetherstonhaugh, D., Slovic, P., Johnson, S. M., & Friedrich, J. (1997). Insensitivity to the value of human life: A study of psychophysical numbing. Journal of Risk and Uncertainty, 14, 283–300.
Frederick, S. (2005). Cognitive reflection and decision making. Journal of Economic Perspectives, 19, 24–42.
Gallistel, C. R. (1990). The organization of learning. Cambridge: MIT Press.
Gallistel, C. R., & Gelman, R. (2005). Mathematical cognition. In K. Holyoak & R. Morrison (Eds.), The Cambridge handbook of thinking and reasoning (pp. 559–588). Cambridge: Cambridge University Press.
Geary, D. C., & Lin, J. (1998). Numerical cognition: Age-related differences in the speed of executing biologically primary and biologically secondary processes. Experimental Aging Research, 24, 101–137.
Gelman, R., & Butterworth, B. (2005). Number and language: How are they related? Trends in Cognitive Sciences, 9, 6–10.
Goesling, B., & Baker, D. P. (2008). Three faces of international inequality. Research in Social Stratification and Mobility, 26, 183–198.
Goldman, D. & Smith, J. (2002). Can patient self-management help explain the SES health gradient? Proceedings of the National Academy of Sciences, 99, 10929 –10934.
Halberda, J., Mazzocco, M., & Feigenson, L. (2008). Individual differences in non-verbal number acuity correlate with maths achievement. Nature, 455, 665–668.
Hauser, M. D., Tsao, F., Garcia, P., & Spelke, E. S. (2003). Evolutionary foundations of number: Spontaneous representations of numerical magnitudes by cotton-top tamarins. Proceedings of the Royal Society, London, B270, 1441–1446.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47, 263–291.
Koechlin, E., Naccache, L., Block, E., & Dehaene, S. (1999). Primed numbers: Exploring the modularity of numerical representations with masked and unmasked semantic priming. Journal of Experimental Psychology: Human Perception and Performance, 25, 1882–1905.
Koehler, O. (1950). The ability of birds to "count". Bulletin of Animal Behavior, 9, 41–50.
Lichtenstein, S., & Slovic, P. (Eds.). (2006). The construction of preference. New York: Cambridge University Press.
Link, S. (1990). Modeling imageless thought: The relative judgment theory of numerical comparisons. Journal of Mathematical Psychology, 34, 2–41.
Lipkus, I. M., Samsa, G., & Rimer, B. K. (2001). General performance on a numeracy scale among highly educated samples. Medical Decision Making, 21, 37–44.
Mather, M. (2006). A review of decision making processes: Weighing the risks and benefits of aging. In L.L. Carstensen & C.R. Hartel (Eds.), When I’m 64 (pp. 145–173). Washington, DC: National Academies Press.
McClure, S. M., Laibson, D. I., Loewenstein, G., & Cohen, J. D. (2004). Separate neural systems value immediate and delayed monetary rewards. Science, 306, 503–507.
Meck, W., & Church, R. (1983). A mode control model of counting and timing processes. Journal of Experimental Psychology: Animal Behavior Processes, 9, 320–334.
Moyer, R. S., & Landauer, T. K. (1967). Time required for judgements of numerical inequality. Nature, 215, 1519–1520.
Nieder, A., Miller, E. K. (2003) Coding of cognitive magnitude compressed scaling of numerical information in the primate prefrontal cortex. Neuron, 37, 149–157.
Parkman, J. M. (1971). Temporal aspects of digit and letter inequality judgments. Journal of Experimental Psychology, 91, 191–205.
Payne, J., Bettman, J., & Schkade, D. (1999). Measuring constructed preferences: Towards a building code. Journal of Risk and Uncertainty, 19, 243–270.
Peters, E., Hess, T. M., Västfjäll, D., & Auman, C. (2007). Adult age differences in dual information processes: Implications for the role of affective and deliberative processes in older adults’ decision making. Perspectives on Psychological Science, 2, 1–23.
Peters, E., Hibbard, J.H., Slovic, P., & Dieckmann, N.F. (2007). Numeracy skill and the communication, comprehension, and use of risk and benefit information. Health Affairs, 26, 741–748.
Peters, E., Västfjäll, D., Slovic, P., Mertz, C. K., Mazzocco, K., & Dickert, S. (2006). Numeracy and decision making. Psychological Science, 17, 407–413.
Piazza, M., Izard, V., Pinel, P., Le Bihan, D., & Dehaene, S. (2004). Turning curves for numerosity in the human intraparietal sulcus. Neuron, 44, 547–555.
Pinel, P., Riviere, D., Le Bihan, D., & Dehaene, S. (2001). Modulation of parietal activation by semantic distance in a number comparison task. NeuroImage, 14, 1013–1026.
Pinel, P., Piazza, M., Le Bihan, D., & Dehaene, S. (2004). Distributed and overlapping cerebral representations of number, size, and luminance during comparative judgments. Neuron, 41, 1–20.
Ratcliff, R. (1993). Methods for dealing with reaction time outliers. Psychological Bulletin, 114, 510–532.
Raudenbush, S., & Bryk, A. S. (2002). Hierarchical linear models: Applications and data analysis methods (2nd ed.). Thousand Oaks, CA: Sage.
Schaalje, G. B., McBride, J. B., & Fellingham, W., (2001, April). Approximations to distributions of test statistics in complex mixed linear models using SAS™ PROC MIXED. Paper presented at SUGI26 Proceedings, Long Beach, CA. Retrieved April 2, 2008, from http://www2.sas.com/proceedings/ sugi26/p262--26.pdf
Siegler, R. S., & Opfer, J. E. (2003). The development of numerical estimation: Evidence for multiple representations of numerical quantity. Psychological Science, 14, 237–243.
Slovic, P. (2007). “If I look at the mass I will never act”: Psychic numbing and genocide. Judgment and Decision Making, 2, 79–95. Retrieved August 25, 2008, from http://journal.sjdm.org/vol2.2.htm
Soman, D., Ainslie, G., Frederick, S., Li, X., Lynch, J., Moreau, P., et al. (2005). The psychology of intertemporal discounting: Why are distant events valued differently from proximal ones? Marketing Letters, 16, 347–360.
Steiger, J. (1980). Tests for comparing elements of a correlation matrix. Psychological Bulletin, 87, 145–251.
Sternberg, S. (1969). The discovery of processing stages. Acta Psychologica 30, 276–315.
Temple, E., & Posner, M. I. (1998). Brain mechanisms of quantity are similar in 5-year-old children and adults. Proceedings of the National Academy of Sciences (PNAS), 95, 7836–7841.
Townsend, J. T. (1992). On the proper scales for reaction time. Hillsdale, NJ: Lawrence Erlbaum.
Weber, E. U., Shafir, S., & Blais, A-R. (2004). Predicting risk sensitivity in humans and lower animals: Risk as variance or coefficient of variation. Psychological Review, 111, 430–445.
Wechsler, D. (1997). Wechsler adult intelligence scale. (3rd ed.). New York: Psychological Corporation.
Wilson, A. J., Dehaene, S., Pinel, P., Revkin, S., Cohen, L., & Cohen, D. (2006). Principles underlying the design of “The Number Race,” an adaptive computer game for remediation of dyscalculia. Behavioral and Brain Functions, 2, 1–14.
Zauberman, G., Kim, B.K., Malkoc, S.A., & Bettman, J.R. (2008). Discounting time and time discounting: Subjective time perception and intertemporal preferences. Journal of Marketing Research. In press.
Table B1. Results of random-effects model of mean correct reaction times.
working memory, processing speed, and vocabulary
Predictor Age group Notation Distance Numeracy Age*Notation Age*Distance Age*Numeracy Notation* Distance Distance*Numeracy Age*Distance*Numeracy Working memory Processing speed Vocabulary Note. Results of random-effects model of mean correct and incorrect reaction times were quite similar, did not show evidence of a speed-accuracy trade off, and are not reported. †p < .10. *p < .05. **p < .01. ***p < .001.
Numbers — you may not use a calculator for any of these questions.
1. Imagine that we roll a fair, six-sided die 1,000 times. (That would mean that we roll one die from a pair of dice.) Out of 1,000 rolls, how many times do you think the die would come up as an even number? Answer:
2. In the BIG BUCKS LOTTERY, the chances of winning a $10.00 prize are 1%. What is your best guess about how many people would win a $10.00 prize if 1,000 people each buy a single ticket from BIG BUCKS? Answer:
people
3. In the ACME PUBLISHING SWEEPSTAKES, the chance of winning a car is 1 in 1,000. What percent of tickets of ACME PUBLISHING SWEEPSTAKES win a car? Answer:
%
4. Which of the following numbers represents the biggest risk of getting a disease?
1 in 100
1 in 1000
1 in 10
5. Which of the following numbers represents the biggest risk of getting a disease?
1%
10%
5%
6. If Person A’s risk of getting a disease is 1% in ten years, and Person B’s risk is double that of A’s, what is B’s risk? Answer:
% in
years
7. If Person A’s chance of getting a disease is 1 in 100 in ten years, and person B’s risk is double that of A, what is B’s risk? Answer:
in
years
8. If the chance of getting a disease is 10%, how many people would be expected to get the disease:
A: Out of 100? Answer:
people
B: Out of 1000? Answer:
people
9. If the chance of getting a disease is 20 out of 100, this would be the same as having a
% chance of getting the disease.
10. The chance of getting a viral infection is .0005. Out of 10,000 people, about how many of them are expected to get infected? Answer:
people
Table B2. General linear model predicting numeracy scores.
R-squared = .17
R-squared = .25
Predictor (df = 1)
(df = 1)
Gender (–1 = male, +1 = female) Age group Distance-effect slope Working memory Processing speed Vocabulary *p < .05. **p < .01. ***p < .001.
In this model of RTs to correct trials, younger adults responded faster than their older counterparts (see Table B1). RTs also differed by notation and distance. The effect of notation and distance did not differ by age, independent of the other predictors in the model. This lack of age difference in the distance-effect slope is consistent with previous literature (Geary & Lin, 1998). The distance effect did differ by notation, consistent with more recent research (Koechlin et al., 1999).
Across the life span, highly numerate individuals were faster than the less numerate at these number-comparison judgments; numeracy was marginally less predictive of reaction times for older than younger adults. In addition, the slope of the distance effect was significantly smaller for the high numerate (the mean RT difference between near and far numbers was –48 and –40 msec for individuals low and high in numeracy, respectively). The effect of numeracy on the distance effect did not differ by age although this effect approached significance (p = .11), with a tendency for a smaller association between numeracy and the distance effect among older adults. The inclusion of measures of working memory, processing speed, and vocabulary substantially reduced the effects of age on comparing numbers in this task, but otherwise had little influence on the results (see far right column of Table B1).
Results of a more traditional repeated-measures analysis of variance (ANOVA) including all main effects and interactions were similar to those of the random-effects model (e.g., the two-way interaction between distance and numeracy was significant, F(1, 137) = 4.09, p < .05). In this more traditional ANOVA, the distance effect did not differ by whether individuals responded larger on the left or on the right (and thus we did not include left/right in the random-effects model for reasons of parsimony).
According to Sternberg’s (1969) classic additive-factors model, the violation of additivity between distance and numeracy indicates that they influence the same stage of processing numbers, namely the internal operation that maps symbolic numbers to the mental number line and determines the quantities of the two compared stimuli (Dehaene, 1996). Thus, the more numerate appear to map numerals to mental representations more precisely than the less numerate. The fact that less numerate people have both longer RTs and a steeper slope has led to the suggestion that reaction times should be transformed to force equivalent slopes. However, as Sternberg has argued effectively, because reaction time is a measure of central nervous system processes, RTs should be treated as interval data (Townsend, 1992). Thus, we use the untransformed mean RT.
Table B3. General linear model predicting distance-effect slopes.
R-squared = .06
R-squared = .10
Predictor Gender (–1 = male, +1 = female) Age group Working memory Processing speed Vocabulary *p < .05. **p < .01. ***p < .001.
Alternative explanations exist for the associations of overall number-comparison speed and distance-effect slope and of numeracy and the slope. One possible explanation for the latter correlation is that individuals with more precise representations are better able to learn higher-order math skills. Our correlational data cannot speak to this possibility, but it is suggestive of interesting future studies in educating math skills and the precision of mental-number-line representations. Recent research in numerical cognition is consistent with this explanation (Dehaene et al., 2008; Halberda et al., 2008).
A second alternative explanation for both correlational results is a scaling artifact. The additive-factors method used to test the link between numeracy and the distance-effect slope requires that RTs be treated as interval data and thus without transformation (Sternberg, 1969; Townsend, 1992); a scaling effect could result in a smaller slope for the highly numerate simply because they are faster and their RTs get closer to a floor compared to the less numerate (Ratcliff, 1993). Past studies in numerical cognition have established a series of three additive component processes or stages in reaction times and event-related potentials to number comparisons (Dehaene, 1996; Temple & Posner, 1998). In particular, a separation appears to exist among the three stages of 1) stimulus identification (manipulated through notation), 2) access to magnitude representations (manipulated through distance), and 3) motor preparation (manipulated through larger being indicated with a left or a right hand press). In a random-effects model of mean correct RTs with distance and notation at Level 1 and left/right, numeracy, and age at Level 2, we tested the interaction of numeracy with each of the three stages. Numeracy interacted significantly only with distance and not with notation or left/right, suggesting that numeracy differentiates the specific effect of distance rather than the other factors. In addition, a comparison of RTs to the Arabic integers 1, 4, 6, and 9 (to a target “5”) between this study and that of Dehaene (1996) suggests that our reaction times do not show a floor effect. In particular, number-comparison responses of Dehaene’s subjects averaged 380 msec compared to 477 msec to the same integers in the present study. The comparison is not a perfect one, however, as Dehaene’s subjects first participated in a pretest to familiarize them with the task and to reject exceptionally slow or fast subjects. The findings that: 1) numeracy was significantly associated with only one of the three factors in the additive-factors method, 2) more extreme reaction times to the same Arabic integers were found in Dehaene (1996), and 3) Halberda et al. (2008) found that more precise representations were associated with better math skills in children who completed a very different number-comparison task (not dependent on RTs) suggest that our results are less likely due to a scaling artifact. Greater numeracy appears to be associated with more precise representations of the mental number line.
We next examine factors that predict numeracy and the distance-effect slope. Previous findings have demonstrated that women score lower than men on numeracy measures; the relation of gender with the precision of representations of the mental number line has not been a focus. First, using a general linear model of numeracy scores, we examined the effects of gender, age group, measures of fluid and crystallized intelligence, and the distance-effect slope. The model was highly significant (see Table B2). Men, younger adults, and those with higher vocabulary scores scored higher in numeracy. The link between numeracy and the distance-effect slope remained after controlling for the other variables in the model. In particular, the b-value for the slope was .03 with and without controlling for the three proxy measures of intelligence.
In predictions of distance-effect slopes, the only significant predictor was processing speed, with individuals who processed information more quickly also demonstrating less steep slopes. See Table B3. Neither gender nor age provided significant, independent prediction of the variability in distance-effect slopes after controlling for the effects of fluid and crystallized intelligence. Older age was predictive of larger distance-effect slopes (less precise representations) without controlling for these proxy intelligence measures.
This document was translated from LATEX by HEVEA.