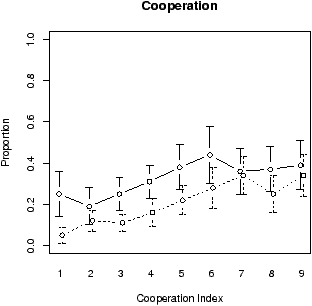
| Figure 2: Mean cooperation and prediction for the games played in the low range and high range conditions. |
Judgment and Decision Making, vol. 3, no. 6, August 2008, pp. 463-475
Debiasing context effects in strategic decisions: Playing against a consistent opponent can correct perceptual but not reinforcement biasesIvo Vlaev* and Nick Chater |
Vlaev and Chater (2006) demonstrated that the
cooperativeness of previously seen prisoner’s
dilemma games biases choices and predictions in the current game. These
effects were: a) assimilation to the mean cooperativeness of the played
games caused by action reinforcement, and b) perceptual contrast with
the preceding games depending on the range and the rank order of their
cooperativeness. We demonstrate that, when playing against choice
strategies that are not biased by such factors, perceptual biases
disappear and only assimilation bias caused by reinforcement persists.
This suggests that reinforcement learning is a powerful source of
inconsistency in strategic interaction, which may not be eliminated
even if the other players are unbiased and the markets are efficient.
Keywords: judgment, cooperation, prisoner’s dilemma, context effects, perception, reinforcement learning.
To explain the behaviour of markets we need a model of the decision-making behaviour of buyers and sellers. To understand how such agents (people and firms) interact in the economy we need to model the strategies people (e.g., managers) select when the outcome of a situation depends also on the decisions of others agents. Thus, an economic understanding of the various markets, of strategic interaction between firms, and indeed of the economy at large, requires understanding how people trade-off payoff and uncertainty when they interact with each other. When decisions are interactive and the outcomes depend also on the decisions of other people, the choice process has a recursive quality: each player makes decisions in the context of assumptions about the decisions of the other player, but the other player may equally choose on the basis of assumptions about the decisions of the first player. Game theory attempts to deal with this recursiveness by introducing the concept of a Nash equilibrium (Nash, 1950, 1951) — a pair of decisions are in Nash equilibrium if neither player would obtain a higher expected utility by making a different decision, given that the other player’s decision is fixed; and game theory continuously refines this notion. (Fudenberg & Tirole, 1991, provide an introduction and review.)
Using experimental methods, psychologists and economists have tested how realistic are such assumptions and approximations, and have found considerable discrepancy between actual behaviour and the predictions of game theory. (See, for example, Kagel & Roth, 1995, for a review.) For example, in any Prisoner’s Dilemma (PD) game, the Nash equilibrium is, notoriously, that both players behave uncooperatively (in real life, the problem of cooperation is that it can secure mutual benefits, but, by cooperating people risk being exploited). However, many studies showed that behaviour of people playing PD game deviates (systematically) from theoretical predictions, i.e., people cooperate more than expected (see Kagel & Roth, 1995). There are various accounts of this behaviour, some including factors such as misunderstanding of the game, role of repetition of the play and the resulting reputation and retaliation affects, irrationality, motivation (incentives, altruism), communication, and so on. (See Sally, 1995, for a review.)
More recently, Vlaev and Chater (2006) tested one of the basic assumptions in game theory that is not typically challenged in experimental work: that each game is considered separately and the resulting choice of strategy should be based only on the attributes of the current game. This study presented a psychological phenomenon, game relativity, which is an anomaly for normative theories of strategic decision-making. Specifically, the reported results seem to indicate that people do not possess a well-defined notion of the utility of a strategy and the “cooperativeness” of a game in particular, and instead, people’s perceived utility for a strategy appears highly context-sensitive and it depends on the other recently played games.
Vlaev and Chater’s (2006) experiments were based on research on fundamental cognitive processes in psychophysics, which are related to perception and representation of sensory magnitudes such as loudness, brightness, or weight. Note that in judging the utility of decision strategies in games, people must assess the magnitudes of risk and return that are associated with each strategy. In this respect, Stewart, Chater, Stott, and Reimers (2003) had earlier argued that some of the factors that determine how people assess these magnitudes might be similar to factors underlying assessment of psychophysical magnitudes. There is substantial evidence that people are poor at providing stable absolute judgments of such magnitudes and are heavily influenced by the other options presented to them in the recent past or available at the time of choice. (See Laming, 1997, for an extensive discussion of this evidence.) Such context effects are consistent with people making perceptual judgments on the basis of relative magnitude information, rather than absolute magnitude information. (Stewart, Brown, & Chater, 2005, provide a model and review.)
Applying these ideas to strategic decision making in PD games, if the representation of the cooperativeness of a game is also similar to the representation of these simple perceptual dimensions (i.e., similar underlying cognitive processes are involved), then preceding material might be expected to influence current judgments and decisions in games, as it does in the perceptual case.1 Vlaev and Chater (2006) tested whether the game’s attributes like “cooperativeness”, measured by Rapoport and Chammah’s (1965) cooperation index (CI)2, behave like those of perceptual stimuli, and they found similar context effects. Here we provide a brief summary of these experiments, which are essential background for understanding the argument behind the follow-up study presented in this article. In the various experiments and conditions of this study, the participants played PD games with varying CI, and we tested whether manipulating properties of the distribution of the CI (like mean, range, and rank) would affect the cooperation rate and the predicted cooperation of the other players.
Experiment 1 tested Helson’s (1964) adaptation-level theory. In contrast to the predictions of adaptation-level theory, we did not find contrast effects, depending on whether a particular game is above or below the mean CI (i.e., the adaptation level) — games above (below) the mean were not perceived as exaggeratedly more (less) cooperative. Instead, the condition with a higher mean cooperativeness caused more, rather than less, cooperation across all game types. This effect of the mean CI can be explained simply by the assumption that cooperativeness is influenced by the amount (frequency) of observed cooperation that participants received, independent of which game they are playing. This fits with reinforcement accounts of game playing, including PD (Erev & Roth, 1998, 2002), which predict that more cooperative games (on average) would lead to more cooperative feedback that reinforces each player to cooperate more across all games. In other words, the mean reinforcement may have caused the observed assimilation effects.
In Experiments 2, the range difference between the games along the CI scale was manipulated while keeping their ranks constant. The range of presented games produced a contrast effect so that that games that were further from the minimum CI value in the sequence were perceived as more “cooperative.” In Experiment 3, we varied the rank order between the games along the CI scale, while keeping their range differences constant, and found that the rank had a significant impact on prediction and choice behaviour. The same game, presented with high rank amongst the other games in the sequence (condition) produced significantly higher cooperation and prediction than when the same game had a low rank. Thus, the results from Experiments 2 and 3 supported the predictions about perceptual contrast, in line with the range frequency theory (Parducci, 1965, 1995), according to which the neutral point of the judgment scale did not correspond to the mean of the contextual events but rather to a compromise between the midpoint defined by the range of the distribution and the median. The neutral point thus depended on the skew of the distribution and was affected by the rank of the particular stimulus in this distribution. For example, satisfaction judgments would be different in two distributions of experiences that have different skew of their intensities or quality levels (and hence will have different rank orders for these stimuli) even if the means of the two distributions are the same.
The contextual effects caused by the mean, range, and rank of the distribution confirmed our expectations that these relativity effects are due to some general underlying cognitive mechanisms. One is related to perception, and in particular, the representation of perceptual magnitudes, as we discussed earlier. The second fundamental mechanism is related to response (action) generation, because agents tend to repeat actions (e.g., C or D) according to the average degree of reinforcement with which each action is associated (i.e., the utility for the agent of the outcome of the game reinforces the chosen strategy). From a psychological point of view, reinforcement corresponds to following Thorndike’s (1911) classic law of effect — repeating behaviours to degree that they are followed by positive outcomes; and stamping out behaviours to the degree that they are followed by negative outcomes. For example, in the context of PD, a reinforcement learner will follow the strategy that brings higher payoff without logical thinking about the strategic structure of the game (in other words, reinforcement learner follows the more rewarding choice instead of inferring the dominant strategy (see Chater, Vlaev, & Grinberg, 2008, for a demonstration of stable cooperation in one-shot sequential play, in which player’s choices are correlated so that they tend to play C when their opponents also play C, and they tend to play D when their opponents also play D, which on average reinforces C). Vlaev and Chater (2006) demonstrate that, when people make interactive strategic decisions, these two principles, perceptual vs. action related, can create biases in terms of overreaction (or under-reaction) to particular attributes of games (like cooperativeness) depending on the environmental distribution of that attribute.
None of the existing studies, however, have investigated whether these context effects also hold when playing against a consistent opponent. Here we do not mean a “rational” opponent who should permanently defect in PD. By a consistent player, we mean a player whose responses are completely determined by the current game, and not influenced either by the structure of previous games, or the history of past responses. Thus, such player is consistent across contexts. Because consistent players are uninfluenced by context, they may potentially act to “damp down,” rather than amplify, contextual effects on the experimental participant — which may arise if both human participants are influenced by the same contextual factors, hence potentially creating a “bubble” of over- and under-cooperating due to the perceptual or response biases. In our study, the consistent player was a computer algorithm, not a human participant (the participants were told this, although the algorithm is not specified). The most psychologically natural model of the consistent player assumes that the probability of cooperation depends on the “cooperativeness” of the game, which is negatively related to the incentive for each player to defect, and also negatively related to the “damage” done to the other player, if one defects. Here we use the cooperation index (CI) which provides a good measure of the typical level of cooperation observed experimentally in PD games (Rapoport & Chammah, 1965).3
The test described in this article is important because it measures the power and sustainability of the perceptual and response biases documented by Vlaev and Chater (2006), which will reveal whether such biases are going to persist in real markets where any overreaction is suboptimal as it can be exploited. In other words, it is good to be cooperative when the situation permits as both players would be better off, if both cooperate4 (even though this logic makes sense only for repeated games, Vlaev and Chater, 2006, have shown that people do expect others to cooperate in one-shot interaction too, even though each player individually always better to defect), but being over-cooperative gives additional incentive to other (less cooperative) players to exploit you.
The unbiased opponent was created by programmed play, in which the participants had to play “against the computer.” In this setting, the computer was pre-programmed to cooperate with a frequency (probability) reflecting the values of the CI of each game. For example, the computer was programmed to cooperate 50% of the time when playing games with index .5. An alternative design would be to program the computer to respond randomly (i.e., to cooperate 50% of the time). However, such a design would not be as powerful evidence about the strength of the biases under question, because the computer generated feedback is more ambiguous about the cooperativeness of the various games (CIs). Thus, players will receive a weaker feedback (signal) when the games are less or more cooperative, and various biases are more likely to thrive in such an ambiguous environment. On the other side, the policy of cooperating according to CI gives less freedom of interpretation about the cooperativeness of the various games.
Note that, even if people think that they are playing a “repeated PD game” (i.e., they think of themselves as playing ‘the same’ program every time, rather than a different person each time), this should not affect our key argument, because, given the program is uninfluenced by prior context, then it does not matter if the game is repeated or not. Actually, if the game is seen as repeated, then that should make the effect of the consistent opponent even stronger, which should, in turn, further weaken the context effects, because the players would be more likely to reciprocate their consistent opponent.
To accomplish our research objective, we replicated the design of the three experiments described by Vlaev and Chater (2006). In particular, the manipulated contextual variables were the parameters of the statistical distribution of the cooperativeness of the games in the sequence — mean, range, and rank — which were equivalent to Vlaev and Chater’s Experiments 1, 2, and 3 respectively. (Here we present the three studies together for brevity of exposition.) The dependent variables were the average cooperation rate in each group, and the expected (predicted) cooperation of the other players.
a) Abstract structure
Other 1 2
b) Cooperation index .1
Other 1 2
c) Cooperation index .9
Other 1 2
Figure 1: The structure of the Prisoner’s Dilemma game: a) Abstract structure; b) Uncooperative game with CI = 0.1; c) Cooperative game with CI = 0.9.
There were 48 participants in this experiment divided into groups of 8 participants per condition with two conditions per distribution manipulation — mean, range, and rank. The participants were recruited from the student population via Oxford University’s Experimental Economics Research Group mailing list. The participants were paid in cash at the end of the session £2 fixed fee and up to £7 in total, with an approximate average of £6 depending on their performance.
Figure 1a illustrates the structure of the PD game. Figure 1b illustrates a very uncooperative game with index .1, while Figure 1c illustrates a very cooperative game with index .9. PD game is defined by the inequality T < C < D < S. We used the abstract version of the game where C is the payoff if both “cooperate” and play 1, D is the payoff if both “defect” and play 2, T is the payoff for the defector who plays 2 while the other cooperates and plays 1, is the payoff for the cooperator who plays 1 while the other defects and plays 2. The game with index .1 is very uncooperative, i.e., it is characterised by high temptation to defect because there is a potential increase of the payoff from the cooperative outcome (CC), which gives 10 units, to the DC or CD outcomes giving 20 units, and a low potential loss if both defect (DD) because the decrease from the outcome with mutual cooperation (CC) to mutual defection (DD) is from 10 to 8 units; while the very cooperative game with index .9 is characterised with a low relative gain from defection because there are only two units increase from CC giving 19 units to DC or CD giving 20 units, and a high potential loss of eighteen units when the comparison is between mutual cooperation (CC) giving 19 units and mutual defection (DD) offering only 1 unit.
Table 1: Prisoner’s Dilemma games used in the experiments.
The initial payoffs of each game were additionally multiplied by 4, 7 and 10 in order to minimise the impact of absolute payoff values on people’s judgments (so there were four versions of each game index in terms of the magnitudes of the payoffs), and in order to control for the effects related to the absolute magnitude of the received payoff from each round and to reduce the salience to participants of the repetition of CI values. Table 1 presents all nine CI game types in terms of their four payoff magnitudes. The three experiments presented in this article used subsets of these games.
In this study, we replicated the design of the experiments described by Vlaev and Chater (2006). Here we provide a summary of the three designs, which manipulated the mean, range, or rank of the distribution of the CI in the experimental session.
Table 2: Distribution of the CI along the whole session in the Low Mean and High Mean conditions.
Condition Cooperation Index 2-10 Low Mean High Mean
There were two between-participants conditions. In both conditions, games were chosen across full range of CI values (from .1 to .9). The different frequencies of games in each condition is shown in Table 2. The numbers in the second and third row of the table represent the frequency of appearance of each CI indicated in the top row. Thus, for example, the game with index .1 appeared 16 times in the Low Mean condition and only twice in the High Mean condition, while game with index .9 appeared twice in the Low Mean condition and in 16 of the trials in the High Mean condition. Thus the mean of the distribution (of the CI) in Low Mean condition was .33 while the mean in the High Mean condition was .67. Helson’s (1964) adaptation-level theory implies that the CI of any individual game will be perceived not absolutely, but in terms of the mean (the adaptation level) of the sequence of games. Therefore, games with CI .4 to .6 should be perceived as much less cooperative when below the mean CI (.67) in the High Mean condition, while these games should be seen as more cooperative when above the mean CI (.33) in the Low Mean condition. Note that in both conditions, games .1 to .3 are below the mean, and games .7 to .9 are above the mean; and therefore these six games should not differ between the conditions. Therefore, according to adaptation-level theory, the average cooperation rate across all games (in the session sequence) should be higher in the Low Mean distribution. On other side, reinforcement account predicts (as shown by Vlaev & Chater, 2006) higher cooperation across all games in the High Mean condition. Note also that, in both conditions of this experiment, each game was in the same position in relation to the other games in terms of range (distance between the ends of the CI scale) and rank.
There were two conditions in the experiment, and there were three CI values per condition. One value, .5, occurred in both conditions. We manipulated between conditions how much higher (lower) this game is from the lowest (highest) game in the sequence. In one condition, games had indexes of .1, .5, and .6, and in the other the indexes were .4, .5, and .9. Thus, the range distance of game .5 from the minimum value of the set is higher in the condition with games .1, .5, and .6, i.e., where this distance is three units (and hence we denote it here as the High Range condition) compared to this range distance in the condition with games .4, .5, and .9, where the distance of game .5 from the minimum value of the set equals only one unit (and denoted here as the Low Range condition). In such a design, we expected the game with index .5 in the High Range condition to be perceived as more cooperative. Note also that the game with index .5 is second in rank in both conditions and thus the rank was not expected to produce any effects.
In this experiment, we kept the range of the presented games the same in all conditions and varied the rank order of the games (in terms of the CI). There were two groups playing games in conditions with different rank order between the games. The first condition included games with index .1, .5, .6, .7, .8, and .9, while in the second condition people played games with index .1, .2, .3, .4, .5, and .9. The expectation was that games with index .5 would be overvalued (perceived as a more cooperative) in the second group because these games are fifth in rank compared with games with index .5 in the first group, in which they are second in rank.
Vlaev and Chater (2006) described these three tests as independent experiments (with two conditions each), but here we summarise them as one study with six independent (between-subject) groups (conditions). In this study, the computer was pre-programmed to cooperate with a frequency reflecting the values of the CI of each game. For example, the computer was programmed to cooperate 10% of the time when CI = 0.1, 50% when CI = .5, and 90% when CI = 0.9.
The participants were informed that the computer was pre-programmed to respond according to the strategy that is used by the majority of people in the context of these particular games (which was true, in the sense that people tend to cooperate increasingly more in games with higher CI). By debriefing the participants at the end of the session, we made sure that they were convinced that the program responds like a human player, because the results may vary depending on whether people think they are playing people like them. If so, they will tend to think the other person will behave like them (presumably — and in fact Vlaev & Chater’s, 2006, prediction data showed this); and people will also tend to play C if they think the other will play C and play D when they think the other will play D — so there is a potential for amplification. On the other hand, if people think they are playing people unlike them, their initial preference to play C does not so directly imply that the opponent (program) is likely to do this too. So that may break the cycle. This pattern is analogous with people investing in a market with other people like them, vs. investing in a market against agents unlike them (e.g., a day trader investing in market governed by programmed trades; or perhaps just by highly sophisticated analysts).


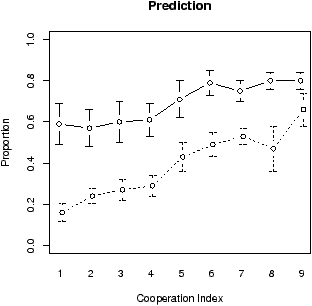
Figure 2: Mean cooperation and prediction for the games played in the low range and high range conditions.
Each condition consisted of a sequence of rounds of PD game. On each round of the game, the participants saw a matrix of the game on the computer screen and they had to make a judgment and a decision (the screen outlook is presented in Appendix A and the instructions are presented in Appendix B).
The judgment was to state how probable it was that the other would play 1 in this game. In order to make an estimation they had to move the slider on the screen, using the pointer of the mouse, to the position between 0 and 100%, which reflected their subjective prediction of the probability (likelihood) that the other player will choose to play “1” in the current round. They were awarded additional points for the accuracy of these predictions and these points were later converted into part payment for the experiment. Note that, even if people played the dominant (rational) strategy (according to game theory) and always defected and expected defection by others), measuring such predictions could still indicate some biases in their perceptions, depending on the previous games. And such subjective prediction is relevant for decision making in games because this judgment should affect people’s choice of strategy (e.g., to cooperate or defect). After making the prediction judgment, the participants had to state how confident they were in this prediction by moving another slider on the screen to the position between 0 and 100%, which reflected their subjective confidence.5 Finally, they had to choose their decision strategy (1 or 2). After both players in each pair (i.e., the participant and the computer) had made their decisions, the round ended and the participants were informed on the screen about the decision made by the computer, and about the received payoff from the game and from the accuracy of the prediction. In order to focus participants’ attention on the differences between the games, it was explicitly stated in the instruction that in every round the payoff values in the matrix would change and we were interested in how these relative changes in the game matrix influenced people’s decision strategy. There was also a detailed explanation of the strategic payoff structure of the game. This aimed to ensure that participants did not stop attending to each game and start playing according to some general rule (e.g., always defect), behaviour that we have observed in the past.
At the end of the experiment the accumulated score (in points) was transferred into cash according to an exchange rate, i.e., the experiment was conducted incentive-compatibly, and thus the participants were paid for their participation in cash according to their performance. The laboratory that we used is equipped with twenty computer terminals, which were isolated in a separate cubical so it was impossible for the participants to see the monitors of the other players or to communicate with them. There were 96 rounds in the session plus four rounds just for training at the beginning of the experimental session, which lasted up to 60 min (including the instructions and the time for training). The games were presented in a different random sequence for each participant.
Figure 2 present the mean cooperation and prediction for every game in each of the two conditions. All results presented here were averaged over all participants in each condition. The error bars represent the standard error of the mean, which is also presented in all other figures. The general trend was that the average cooperation increased as the CI increases in value, which indicates that the participants were sensitive to the index and showed differential behaviour depending on the values of the index. There was a higher cooperation rate on average (over all games and participants) in the negatively skewed distribution, where the mean rate was 0.38, compared to the positive skew condition, where the cooperation rate was 0.14, and this difference was statistically significant, t(14) = 2.27, p = .039. The general pattern in the results was that participants expected more cooperation as the value of the CI increased in each condition, and also there was higher predicted cooperation for almost every game in the negatively skewed condition compared to the positively skewed one. The average prediction rate across all games was significantly higher in the negative skew condition compared to the positive skew condition where the mean prediction in the negative skew was 0.75 versus 0.30 in the positive skew, t(14) = 7.32, p < .001.
Figure 3: Mean cooperation and prediction for the games played in the low rank and high rank conditions.
The figures for the mean cooperation rates and mean prediction for all games in every condition are shown in Figure 3. Again, in both conditions, there was a clear tendency the cooperation to be higher in games with index .6 than in games with index .5, which indicates that the participants were sensitive to the difference between these games. However, there was no significant difference between the cooperation in the low range and high range conditions, t(14) = 0.77, p = .450; this result could be taken as an evidence that the participants tended in their choice strategy to reciprocate the programmed responses of the computer. The prediction responses in the high range condition show pure assimilation effect towards the mean CI in this condition, which equals ∼.40 (and indeed the mean predictions in the three games are all just above this mean value of the CI). The responses in the low range condition were not assimilated and show a linear tendency to increase along the CI. For this design, the difference between the average prediction rate for game with index .5 in the two conditions was not statistically significant, t(14) = 1.41, p = .179, which is most likely due to the conditioning effect of the unbiased programmed feedback.
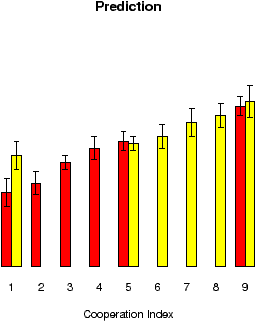
Figure 4: Mean cooperation and prediction for the games played in the low rank and high rank conditions.
The figures for the mean cooperation rates and mean prediction responses for all games and averaged over all participants in every condition are shown in Figure 4. As before, the general trends is that both the cooperation and prediction responses increase proportionally (roughly linearly) to the CI, which indicates participants’ differential behaviour with respect to the CI. However, the difference between the average cooperation rate for game .5 in the Low Rank and High Rank conditions was not significant t(14) = 0.32, p = .757, which suggests that people tend to match their choices to the programmed frequencies of cooperation, and this might be interpreted as a form of a tit-for-tat strategy against the computer. There was also not significant difference between the predictions for games with index .5 in the Low Rank and High Rank conditions, t(14) = 0.12, p = .904. This result again suggests that the participants were very sensitive to the programmed response and can learn to predict the relative frequencies produced by the computer; which probably enables them also to form an absolute judgment of the cooperativeness of the games, and the context effects are not strong enough to counter this effect.
In this programmed design, we did not observe perceptual contrast effects caused by the range and the rank on both cooperative choices and prediction judgments (however, Vlaev & Chater, 2006, observed such contrast effect during interactive play) when the opponent plays unbiased strategy reflecting the cooperativeness of each game. This elimination of perceptual biases is most likely due to the conditioning effect of the programmed strategies of the opponent and indicates that people tend to reciprocate the strategy of the other player (i.e., what they think the other player will do). However, such judgment and choice conditioning was not found when the frequency of the different CIs was manipulated, which affected the mean cooperativeness in each condition. This result shows a very striking dissociation between the biasing effects of perception and action reinforcement; and implies that the latter is more powerful biasing force in decision making.
In summary, the assimilation persists in Experiment 1 and the “debiasing” in the other two experiments is attributed this to the consistent strategies used by the computer opponent. We do not think that the results can be attributed just to the effect of playing a computer opponent, because the participants were affected by the cooperation rate, as if the computer were a person. Thus, the players were reciprocating the computer as if it were like any other human opponent. Also, note that the magnitude of the “assimilation bias” is comparable to our earlier study — the average difference (High minus Low) in the earlier study is 0.18 vs. 0.24 in this study; which demonstrates that the participants in both studies responded to their opponents in a similar way irrespectively of whether they play against human or computer opponent. Therefore, if we program the computer to play in those conditions as the human opponents did (i.e., to be “biased”), then the participants play will be biased too (and also, we will not be able to differentiate between “genuine” perceptual bias and bias due to reciprocating the biased computer).
We use the term of manipulating ranks in the rank condition but not in the mean condition. However, some interpretations of range-frequency theory (Parducci, 1965, 1995) would consider both rank manipulations, but one based on relative frequencies and the other based on relative stimulus spacing. These often produce the same effects (Parducci & Perrett, 1971), but can produce different effects (Parducci & Wedell, 1986). Thus, there is an issue whether rank effects could be explained by relative differences based either on the “type” of the contextual stimuli (i.e., stimulus spacing matters — e.g., CI .5 is subjectively judged as .6 after seeing .1 and .3, and as .7 after seeing .1, .2, .4), or on the “tokens” (exemplars) in the context (i.e., frequencies change how each item is judged — e.g., .5 may be seen as .6 after .4 is presented five times and as .7 after .4 is presented ten times). Our assumption here is that only “type”, not “token” effects matter — i.e., people do not change their subjective perception of the CI values irrespectively of how many times they see each CI (e.g., seeing five times game with index .4 and ten times game with index .5 does not change how .6 game is perceived and ranked). This strong assumption, partially motivated by the unresolved ambiguity on this issue in the psychophysics literature, is also supported by two empirical findings. First is that, if not instructed otherwise, people have a tendency to repeat the same responses to the same stimuli (Haubensak, 1992). And second, in our earlier study (Vlaev & Chater, 2006) we demonstrated, using the “game differentiability” test, that people can reliably rank the games along the full continuum of the CI, which indicates that all levels can reliably be identified and categorized as separate “types.” In summary, in our study we assume that judgment is affected by how many (not how often) CI levels below the target items are presented in the session.
Even if our interpretation of range-frequency theory is too strong, and raw frequencies matter, it is still the case that the frequency (token) based effects in Experiment 1 (if they exist) should work in the opposite direction — producing contrast (similar to adaptation-level theory), not the observed assimilation. Thus, in the Low Mean condition, higher CI levels should be overvalued due to the many low-rank CIs, while in the High Mean condition, lower CI levels should be undervalued due to the many CIs with higher rank, and as a result, range-frequency predicts higher ratings in the Low Mean condition (or no effect at all due to the consistent pre-programmed response). So, the fact that we observed assimilation effect (i.e., higher ratings in the High Mean condition) speaks against the existence of mere frequency based rank effects. Note also that Vlaev and Chater (2006) also interpreted rank effects as caused by relative spacing (types) (Experiment 3), not relative frequencies (tokens), and the latter was again interpreted as assimilating effect of the mean (Experiment 1).
In the mean manipulation design, the assimilation of judgment and choice behaviour is a suboptimal (Pareto-inferior) bias, because it does not reciprocate the feedback from the other player (i.e., the participants cooperate too much relative to the frequency of the opponent, and thus risk to be exploited because they are more likely to choose C when the opponent plays D). Such behaviour is most likely caused by different average reinforcements received in the two conditions. Note that reinforcement learning methods are based on the average amount of reinforcement that each behaviour (i.e., the two responses C or D) actually receives. Such a reinforcement difference would appear when only the mean is manipulated, and as a result the average payoff received for C will be higher in the condition with more cooperative games; because each time a player chooses C in this condition, the other player is more likely also to play C, while in the less cooperative condition, C response is more likely to meet a D response. In other words, reinforcement learning is driving behaviour by using the mean received reward (payoff) for each action as a guide to change the probability for each action accordingly. This happens even though the response of the computer did not change between the two conditions. We have already shown similarly powerful effect of reinforcement in causing sustained cooperation when players’ choices are correlated by an exogenous factor (e.g., the cooperativeness of the specific PD chosen), because thus they obtain greater average reinforcement for cooperating than for defecting (Chater, Vlaev, & Grinberg, 2008).
The fact that C gets higher payoff on average in the negatively skewed condition also answers the question whether action reinforcement versus predicted reinforcement is driving choice behaviour. If predicted reinforcement (punishment) was behind players’ actions then there will be more defection in the more cooperative condition where D play is more likely to meet a C response, which is more profitable than D meeting D play. The increased cooperation in the cooperative condition, therefore, suggests that actual reinforcement (instead of anticipated reinforcement) was guiding judgment and choices behaviour. This conclusion is also supported by Vlaev and Chater’s (2006) finding that the assimilation was caused only by reinforcement and not by perceptual assimilation (see Experiment 1B).
Note that the persistence of the reinforcement bias is even more striking when people are playing a computer, which should make people less biased, because there is no amplification of biases typically observed when playing against other humans (i.e., when people may think other players have the same biases and want to do the same as them). The reinforcement bias is also surprising if we assume that the participants were playing a “repeated PD” with the program, because then the players should be more likely to reciprocate their consistent opponent, which should make the effect of the consistent strategy even stronger (i.e., the results should be less biased), which did not happen in our study.
The type of sequential effects found in psychophysical research on judgment is also of interest here, because it sheds light on the dynamics of the judgment and choice process. The responses, regarded as a time series, show autocorrelational structure. Typically the data are analysed using multiple regression in which the stimulus and the response on the preceding trial enter as predictors after the contribution of the current stimulus has been factored out (accounted for). A robust finding is that current responses tend to be contrasted (i.e., negatively correlated) with previous stimuli and assimilated (positively correlated) toward previous responses. Moreover, there is an interaction between the previous stimulus and previous response as two time-lagged variables. The assimilation towards the previous response seems to be modulated by the difference between the previous and current stimulus (Jesteadt, Luce, & Green, 1977; Petzold, 1981). The closer are the stimuli, the stronger is the assimilation. In the mean manipulation study, the CIs were closest to each other — the difference was only one unit on the CI scale as all nine levels were presented in the sequence (while in the range and rank manipulations, the difference between some of the stimuli was much bigger), which must have had an amplifying effect on the assimilation. Note that the assimilation would be even more magnified due to the incentive structure of the game task where responses are rewarded with payoffs (something not done in standard psychophysical tasks), which adds extra weight (importance) to actions relative to perceptions.
In summary, when there is nothing in the distribution of games that could affect (and bias) people’s perception of the cooperativeness of each game, judgments and choices are simply based on the average reinforcement of each action (strategy C and D respectively) and also on the absolute cooperativeness of the game (indicated by the sensitivity to the CI). Thus, the main conclusion from this experiment is that the mean of the distribution (when there is no variability of the range and the rank) causes strong contextual biases, and even playing consistent opponents cannot overpower the assimilation effect based on action reinforcement. Such biases are likely to emerge in real markets, when, for example, a company is competing in different business environments (varying in cooperativeness) and managerial choices reflect pricing decisions and revenues (also, see any management textbook for many business cases represented as PD type of situations). A variety of other real world settings may have the structure of a PD game, including trade talks, arms races, and pollution control. Therefore, our results have serious implications for such cases.
Our results also have implications for economic models, in which reinforcement learning models can provide tractable and plausible models of economic behaviour in various economic contexts (see Erev & Roth, 1998, 2002, for examples). Note that the effects on predicted cooperation also imply that we can create economic institution (or business environments), which promote the subjective perception and expectation of cooperative environment. This, in turn, might increase the social capital in the community of managers, employees, or neighbours.
Bonacich, P. (1972). Norms and cohesion as adaptive responses to potential conflict: An experimental study. Sociometry, 35, 357–375.
Chater, N., Vlaev, I., & Grinberg, M. (2008). A new consequence of Simpson’s paradox: Stable cooperation in one-shot prisoner’s dilemma from populations of individualistic learning agents. Journal of Experimental Psychology: General, 136 (3), (lead article).
Fudenberg, D., & Tirole J. (1991). Game theory. Cambridge, MA: MIT Press.
Garner, W. R. (1953). An informational analysis of absolute judgments of loudness. Journal of Experimental Psychology, 46, 373–380.
Goehring, D. J. & Kahan, J. P. (1976). The uniform n-person prisoner’s dilemma game: Construction and test of an index of cooperation. Journal of Conflict Resolution, 20, 111–128.
Haubensak, G. (1992). The consistency model: A process model for absolute judgments. Journal of Experimental Psychology: Human Perception and Performance, 18, 303–309.
Helson, H. (1964). Adaptation-level theory. New York: Harper & Row.
Holland, M. K., & Lockhead, G. R. (1968). Sequential effects in absolute judgments of loudness. Perception and Psychophysics, 3, 409–414.
Jesteadt, W., Luce, R. D., & Green, D. M. (1977). Sequential effects of the judgments of loudness. Journal of Experimental Psychology: Human Perception and Performance, 3, 92–104.
Kagel, J. H., & Roth, A. E. (1995). The handbook of experimental economics. Princeton, NJ: Princeton University Press.
Kelley, H. H., & Thibaut, J. W. (1978). Interpersonal relations: A theory of interdependence. New York: Wiley.
Laming, D. R. J. (1997). The measurement of sensation. London: Oxford University Press.
Lockhead, G. R. (1984). Sequential predictors of choice in psychophysical tasks. In S. Kornblum & J. Requin (Eds.), Preparatory states and processes (pp. 27–47). Hillsdale, NJ: Erlbaum.
Nash, J. F. (1950). The bargaining problem. Econometrica, 18, 155–162.
Nash, J. F. (1951). Noncooperative games. Annals of Mathematics, 54, 289–295.
Parducci, A. (1965). Category judgment: A range-frequency theory. Psychological Review, 72, 407–418.
Parducci, A. (1995). Happiness, pleasure and judgment: The contextual theory and its applications. Mahwah, NJ: Lawrence Erlbaum.
Parducci, A., & Perrett, L. F. (1971). Category rating scales: Effects of relative spacing and frequency of stimulus values. Journal of Experimental Psychology Monograph, 89, 427–452.
Parducci, A., & Wedell, D. H. (1986). The category effect with rating scales: Number of categories, number of stimuli, and method of presentation. Journal of Experimental Psychology: Human Perception and Performance, 12, 496–516.
Petzold, P. (1981). Distance effects on sequential dependencies in categorical judgments. Journal of Experimental Psychology: Human Perception and Performance, 7, 1371–1385.
Rapoport, A., & Chammah, A. (1965). Prisoner’s dilemma: a study in conflict and cooperation. Ann Arbor: University of Michigan Press.
Sally, D. (1995), Conversation and cooperation in social dilemmas. A meta-analysis of experiments from 1958 to 1992, Rationality and Society, 7, 58–92.
Steele, M. W., & Tedeschi, J. T. (1967). Matrix indices and strategy choices in mixed-motive games. Journal of Conflict Resolution, 11, 198–205.
Stewart, N., Brown, G. D. A., & Chater, N. (2002). Sequence effects in categorization of simple perceptual stimuli. Journal of Experimental Psychology: Learning, Memory, and Cognition, 28, 3–11.
Stewart, N., Brown, G. D. A., & Chater, N. (2005). Absolute identification by relative judgment. Psychological Review, 112, 881–911.
Stewart, N., Chater, N., Stott, H. P., & Reimers, S. (2003). Prospect relativity: How choice options influence decision under risk. Journal of Experimental Psychology: General, 132, 23–46.
Thorndike, E. L. (1911). Animal intelligence: An experimental study of the associative processes in animals. Psychological Review Monograph Supplement, 2, Whole No. 8.
Vlaev, I., & Chater, N. (2006). Game relativity: How context influences strategic decision making. Journal of Experimental Psychology: Learning, Memory, and Cognition, 32, 131–149.
Appendix A: Screen outlook

Ward, L. M., & Lockhead, G. R. (1970). Sequential effect and memory in category judgment. Journal of Experimental Psychology, 84, 27–34.
Ward, L. M., & Lockhead, G. R. (1971). Response system processes in absolute judgment. Perception & Psychophysics, 9, 73–78.
Zizzo, D. J., & Tan, J. H. W. (2003). Game harmony as a predictor of cooperation in 2 x 2 games. Oxford University Department of Economics Discussion Paper n. 151.
Welcome to the Department of Economics. You are about to take part in an experimental study of interactive decision-making. You will be paid for your participation in cash depending on your performance, and hence different participants may earn different amounts.
This experiment will consist of some number of interactive rounds of the decision making game shown on the computer screen. What you earn depends partly on your decisions and partly on the decisions of the computer. You will be playing against a pre-programmed strategy. The strategy is generalized from previous experiments with these games in which people had to play against each other, so the strategy reflects real human behaviour.
The rules of the game are the following. There are two players in this game — YOU and the OTHER player. After you have been paired, each player is simultaneously be asked to make a choice according to the structure of the game presented as the matrix that is shown on the computer screen. Your decision options are presented as the two rows of the matrix and you can choose either row 1 or row 2, and the decision options of the other player are presented as the two columns in the matrix, as either column1 or column 2. After each player has made a choice, payoffs for the round are determined based on the choices made. There are four possible outcomes of the game organized as the four cells in the matrix. The outcome of the game is the cell where the chosen row and column strategies (1 or 2) cross with each other. Payoffs to each player are indicated by the numbers in the cells of the matrix. The payoffs to you are in red and appear in the left side of each cell, while the payoffs to the other player are in blue and appear in the right of each cell. The units are in points. Thus, if you choose 1 and the other player chooses 1 you receive a payoff of 2 points, while the other player receives a payoff of 2 points. If you choose 1 and the other chooses 2 then you receive a payoff of 0 points while the other receives a payoff of 4 points. If you choose 2 and the other player chooses 1 then you receive a payoff of 4 points, while the other player receives a payoff of 0 points. Lastly, if you choose 2 and the other subject chooses 2, you receive a payoff of 1 point, while the other receives a payoff of 1 point.
In every round the values in the matrix will change and we are interested in how these changes influence people’s strategy for making decisions. So, do pay attention to the relative changes of the payoff values. The computer is pre-programmed to respond intelligently according to the strategy that is used by the majority of people when they play these particular games. So in order to play optimally you will have to pay attention to the variation of the payoffs in the game matrix.
Throughout the experiment, you will be told what is currently happening at the bottom of the screen in the same box in which is the instruction you are reading at the moment. The history table shows the history of your previous rounds.
In addition, in each round before making your choice you have to make two judgments:
(1) The first question will be “How probable do you think it is that the other player will play 1 in this game?” In order to make an estimation you need to move the slider on the screen, using the pointer of your mouse, to the position between 0 and 100, which reflects you subjective prediction of the probability (likelihood) that the other player will choose to play 1 in the current round, and then click the button “OK” positioned on the right side of the slider. Note that you will be awarded additional points for the accuracy of your predictions in each round. This is the scheme on which the guess payments are determined. If you are 100% correct in your prediction then you double your received points. If you are 0% correct then you will receive only the points from the game. In general, for every percentage point your guess is `out’, i.e., the difference between your predicted probability and the other’s choice, a deduction is made from an amount equal to the received amount from the game. Thus for example, if your payment from the round is 10 points and you are 50% correct in your prediction that the other will play 1 in the current round, then you will gain 5 points in addition to the 10 points received from the game. If your gain is 0 points then of course your prediction will not affect your additional gain.
(2) The second question is “How confident are you in your estimation?” and is related to your subjective confidence in your first estimation of the probability that the other player will choose 1. Again, you have to use the slider on the screen, and by using the pointer of your mouse, to move the slider to the position between 0 (indicating no confidence at all) and 100% (indicating that you are absolutely certain). There will be no reward to for this task but please take this task seriously as well.
In every round the values in the matrix will change. The ratios between the payoffs differ and you have to pay attention to the relative values of the payoffs in each game in order to make good decisions and correct predictions. In some games it might be more rewarding not to go for the highest possible payoff and it could be more strategic to choose the other alternative. Your final earnings in cash will be the sum of your payoffs from all rounds plus the rewards based on the correctness of your predictions.
Now feel free to play with the game and sliders on the screen in order to get used to the procedure. When you feel ready to start the experiment and play for real click the button “Start” with the pointer of the mouse.
This document was translated from LATEX by HEVEA.