Judgment and Decision Making, vol. 3,
no. 2, February 2008, pp. 181-190
The effects of total sleep deprivation on bayesian updatingDavid L. Dickinson* 1, and Sean P. A. Drummond2,3
1 Dept. of Economics, Appalachian State University
2 Department of Psychiatry, Laboratory for Sleep and Behavioral
Neuroscience,
University of California, San Diego
3 Psychology Service, Veterans Affairs San Diego Healthcare
System |
Subjects performed a decision task (Grether, 1980) in both a well-rested
and experimentally sleep-deprived state. We found two main results: 1)
final choice accuracy was unaffected by sleep deprivation, and yet 2)
the estimated decision model differed significantly following
sleep-deprivation. Following sleep deprivation, subjects placed
significantly less weight on new information in forming their beliefs.
Because the altered decision process still maintains decision accuracy,
it may suggest that increased accident and error rates attributed to
reduced sleep in modern society stem from reduced auxiliary function
performance (e.g., slowed reaction time, reduced motor skills) or other
components of decision making, rather than the inability to integrate
multiple pieces of information.
Keywords: Bayes rule, uncertainty, information, experiments, sleep.
1 Introduction
A large volume of evidence suggests that individuals in industrialized
nations are becoming increasingly sleep-deprived. According to a
recent poll conducted by the National Sleep Foundation, the
average American adult slept less than 7 hours per night in 2005. The
nightly average was 7.5 hours in 1975 and 9 hours per night in 1910
(Coren, 1996). This trend has significant implications given the known
effects of sleep deprivation: decreased motor and cognitive
performance, reduced vigilance and reaction time, worsened mood, and
reduced ability to think flexibly (Pilcher & Huffcutt, 1996; Harrison
& Horne, 1999, 2000). Indeed, even 7 hours of habitual sleep per
night leads to significantly diminished cognitive performance relative
to 8 or 9 hours (Van Dongen, et al, 2003; Belenky, et al., 2003), which
causes us to wonder about the more hidden decision effects of
sleep loss. Nearly 50 million Americans, close to 25% of all adults,
are estimated to suffer from some level of sleep deprivation,1 and so the
effects of sleep deprivation on decision-making have widespread
implications.
Many occupations promote a culture of sleep deprivation (e.g., emergency
personnel, air traffic controllers, medical residents, military
personnel, long-haul truck drivers, shift workers). Sleep deprivation
costs the U.S. economy $40 billion dollars annually in lost
productivity (Stoller, 1997). Additionally, it results in increased
workplace accident rates (Melamed & Oksenberg, 2002; Akerstedt et al,
2002), increased absenteeism (Phillips et al., 1991; Kupperman et al.,
1995), greater medical morbidity and related costs (Drake et al.,
2004), and even slower career advancement (Johnson & Spinweber, 1983).
Across numerous settings (work, home, driving, public accidents) Leger
(1994) estimated the costs of accidents attributable to sleepiness at
$43-$56 billion, in 1988 dollars. Sleep deprivation has also been
implicated in several major historical disasters, including the Space
Shuttle Challenger explosion, the Exxon Valdez oil spill, and the
Chernobyl Nuclear plant explosion (Coren, 1996). In sum, the impact of
sleep deprivation in the workplace and on society as a whole, while
difficult to measure precisely, is massive.
This paper reports results from a laboratory study that examines the
effects of sleep deprivation on information processing. Examinations
of flexible thinking, strategy updating, and risk assessment are
relatively new to sleep research (see references in Harrison & Horne,
2000; McKenna et al, 2007, Killgore et al, 2006). Past research has
utilized complex multi-modal tasks or operational settings that cannot
identify specific aspects of decision-making affected by sleep
deprivation. For example, Harrison and Horne (1999) utilize a
marketing simulation game, and they report that 36 hours of total sleep
deprivation led to stereotyped decisions failing to integrate previous
feedback, resulting in large financial losses and production errors.
In operational settings, similarly global outcome measures are reported
(e.g., Friedl et al., 2004; Weinger and Ancoli-Israel, 2002). A recent
meta-analysis of 60 studies found that “clinical
outcomes”, the culmination of many decisions, were
negatively impacted by physician sleep loss (Philibert, 2005).
Thus, neither laboratory nor applied sleep deprivation studies have
measured discrete, quantifiable decision parameters free of confounds.
Even the well-known Iowa Gambling Task (IGT), which has been used to
examine risky choice behavior in the sleep literature (Killgore et al.,
2006), does not allow the researcher to separate risk attitude from
subjective probability formation — the latter results from the fact
that there is missing information with respect to outcome probabilities
in the IGT. McKenna et al. (2007) addressed this issue and showed that
sleep deprivation desensitizes the decision-maker to risk.
In general, the mechanism by which sleep deprivation alters decision
making remains unclear. Given that many real-world decisions involve
multiple cognitive processes, it is important to separately examine
several of those components in an effort to determine which may be
specifically impacted by sleep deprivation and which may not. The
studies examining risk preference cited above are examples of such
work. Another process found in many decisions is the ability to
integrate multiple pieces of information into a decision. Sleep
deprivation might alter subject tendencies to utilize one or more
pieces of information in decision-making.2 Or, the arrival of new information
may elicit an impulsive response as subjects react to new evidence, and
this impulse may be altered following sleep deprivation. The current
study examines this specific aspect of decision-making through the
study of Bayesian updating. The experiment is administered to subjects
both well-rested and after 22–25 hours (µ=22.72,
σ=.60) of controlled total sleep deprivation. For
comparison to previous economics research, we replicate the Bayes rule
experiment of Grether (1980).
One can examine the effects of sleep deprivation on the ability to
integrate information into a decision from at least two perspectives,
each with their own strengths and weaknesses. One involves asking
whether individuals can calculate the true Bayesian probability given
base rate probabilities and new sample evidence. This requires asking
subjects for their judgment of the actual probability of event A
occurring and, therefore, focuses on finding the
“ideal” answer to a problem.
Although this approach has merit, our interest was in determining the
weight placed on the odds and evidence when an actual forced choice was
made (i.e., A was more likely to occur). Such a scenario is more
aligned with many naturally-occurring decision environments in everyday
life. For example, one may have to decide which of two routes to a
destination is faster right now given the prior knowledge of
the rate of traffic on each route and the new information of the
current day and time. A surgeon may have to decide to perform an
emergency procedure given prior knowledge of the relative success of
the procedure and the new information of the current condition of the
patient. In short, when individuals make real decisions, they must
often choose a specific course of action (i.e., a dichotomous choice)
rather than a probability estimate. It is the influence of sleep
deprivation on making such decisions that is our interest.
Because information updating is a fundamental component of decision
making under uncertainty, this research is relevant to a wide variety
of behavioral applications. Sleep research has indirectly pointed
towards failed information assimilation under sleep deprivation (e.g.,
increased hesitance and reduced focus among sleep-deprived junior
doctors in Goldman et al, 1972, and increased stereotyping of
responses in Harrison & Horne 1997, 1998). However, more direct
evidence is needed, and Harrison and Horne (2000) recognize the lack
of sleep deprivation research on specific decision models. As
behavioral economics continues to explore decision-making, one cannot
ignore the evidence indicating that many decision-makers are often
sleep-deprived to some degree. Sleep loss effects on decision-making
would also imply a potential confound in some experimental data sets:
students employed as shift workers, or students during exam week, may
include relatively more sleep-deprived subjects than other
populations.3
2 Methods
As noted, the experiments replicate the Grether (1980) design for a
hand-run Bayes rule decision task. Two bingo cages are each filled
with six colored balls: Cage A is filled with four green and two red
balls, and Cage B is filled with three red and three green balls. Six
draws, with replacement, were made from one of the cages behind an
opaque divider. Each subject was informed of a
“prior” probability of using Cage
A in terms of a die roll. For example, a 1/3 prior odds of Cage A was
implemented by selecting Cage A if the die roll was 1–2 (3–6 implied
use of Cage B). Subjects did not see the actual die roll but were
shown each ball drawn, and after six draws they were asked to indicate
whether the balls came from Cage A or B.
It is important to note that we do not vary the new evidence sample size
in our design, rather just the strength of the evidence in favor of
Cage A. Griffin and Tversky (1992) show that, though both strength of
evidence and sample size contribute to the likelihood ratio
for the event in question, subjects place more weight on the sample
proportion in favor of a particular outcome. Our results, therefore,
do not speak to subject weighting on new evidence in general, but
rather new evidence as represented by sample proportion in our
design.4 It would, however, be interesting to explore
the weight of evidence through sample size as another manipulation for
future research. Importantly, subjects in our design were not
required to memorize the sample drawn, which would confound our task
with short-term memory skills. A correct (incorrect) cage response
resulted in payment of $12 ($2).
Each round or trial — choose the cage, draw the sample, indicate which
cage was used — was repeated six times, with one well-rested and one
sleep-deprivation trial randomly selected for payment after the final
Bayes rule experiment — subjects did not know their accuracy or
winnings until after all decisions were made. The design was balanced
across prior A odds of 1/3, 1/2, and 2/3, which occurred in a random
order chosen for each subject.5 Because an accurate cage choice pays more, it is incentive
compatible to indicate Cage A if one’s subjective
(posterior) probability of Cage A is greater than 50%. A Bayesian
subject will equally consider both the prior odds and sample evidence
in making choices.
2.1 Subjects
A total of 24 subjects, were administered the Bayes rules experiment as
part of their participation in a total sleep deprivation study, which
involved a stay of several consecutive nights and days in the
Laboratory for Sleep and Chronobiology at the University of
California-San Diego.6 These 24
subjects ranged in age from 18 and 39 years of age (µ=23.83,
σ=5.37), Subjects were compensated a flat fee for
participation in the sleep study, but it was made clear that these
experiments afforded the opportunity to earn extra cash payoffs based
on the experiment outcomes. Testing on various cognitive dimensions
occurred approximately every two hours during their lab stay. Each
subject completed the basic 30-minute (6-trial) Bayes rule experiment
twice; once in a well-rested state, and once after 22–24 hours of total
sleep deprivation. Both administrations of the task occurred during
morning hours for all subjects, so that there is no confound between
sleep loss and natural circadian sleep-wake cycles. The total number
of observations is N=288 (N=144 well-rested and N=144 following sleep
deprivation).
Screening criteria allowed right-handed, healthy, and
“normal” sleeper subjects — those
with consistent sleep-wake schedules to include 7–9 hours in bed each
night. Subjects are indirectly monitored for one week prior to
reporting to the sleep lab by keeping a sleep journal and wearing an
actigraph.7 During this
week, subjects are required to keep normal sleep-wake routines and
refrain from use of stimulants for 72 hours prior to reporting to the
lab. In short, all subjects (including Control subjects, discussed
later in this section) enter the lab in a similar well-rested state.
During the total sleep deprivation treatment, subjects were not allowed
any sleep, not allowed stimulants of any sort, and they were under
constant supervision by lab staff to ensure this. Figure 1 describes
the basic timeline of the subjects’ lab stay relative
to their participation in these decision experiments.
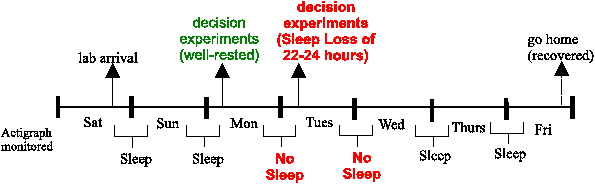
| Figure 1: A week in the sleep lab: time line. (Some subjects stayed in
the lab one less day and participated in a one-night sleep-deprivation
study. Our examination of sleep-loss effects after one night of sleep
deprivation allowed us to combine subjects from different sleep
studies, whether they participated in a one-night or two-night study.) |
2.2 Experimental design issues
In a more recent paper, Grether (1992) notes that there are limitations
to his simpler 1980 design. The dichotomous choice of Cage A or B does
not allow us to infer strength of belief (i.e., 55% versus 95%
certain that the balls came from Cage A), though this is possible using
a rather complicated incentive compatible probability elicitation
procedure (see Grether, 1992). As noted earlier, the dichotomous
choice environment more closely mirrors naturally-occurring decision
environments. Additionally, the more simple dichotomous choice design
is easier to understand, which is important given that subjects
complete one of the trials following sleep deprivation. On the other
hand, the dichotomous choice environment implies that simple decision
heuristics may be available, which could possibly confound an
examination of Bayesian updating. We present data and analysis,
however, that strongly support the conclusion that subjects weight
both prior odds and new evidence in making their decisions.
Because of the existing sleep protocol, subjects always performed the
task first well-rested and then following sleep deprivation. Given the
potential learning confound in our main data, we also recruited an
additional 12 control subjects (mean age µ=24.12,
σ=4.28) who performed the Bayes rule task twice (N=144 total
observations), at approximately 22–24 hours apart on consecutive
mornings, but they were well-rested both times. Decision model
estimates for the control subjects show no significant
differences across the two administrations of the task — contrary to
the main finding in the sleep deprivation data. In other words, we
find no evidence that the differences in decision-making we report in
the next section are due to subject learning. Additionally, if
subjects learned, choice accuracy would be higher in the second Bayes
rule experiment, but it is not. Or, learning might imply that a
particular empirical model should better fit the data as choices
converge to a particular set of model parameters — Grether (1980) finds
this for experienced subjects, for example. Our results also show that
this is not the case. We are therefore confident in attributing the
second-trial effects to sleep deprivation.
3 Results
Table 1 shows the aggregate data in terms of the proportion of overall
subject choices of Cage A relative to the total observations for a
particular combination of prior odds, PA, and evidence.
For comparison, the Bayesian posterior probabilities — those
calculated by Bayes rule — are included in parenthesis in each
instance. At this point, the aggregate data offer the best estimate of
overall “strength of belief” for
our pooled data, given that each individual subject makes a simple
dichotomous choice. A quick scan of Table 1 clearly highlights that,
holding PA constant, the proportion of subject choices
of Cage A increases as the evidence favors Cage A (i.e., as more green
balls are drawn in the sample evidence). It is also the case that,
holding the evidence constant, the proportion of choices of Cage A
rises with PA. Both of these observations are true for
the well-rested and sleep-deprived subsamples. In short, the evidence
is supportive of the hypothesis that subjects care about both prior
odds and evidence in forming belief. We next turn to our decision
model estimates to examine relative weights placed on each source of
information.
| Table 1: Proportion of Cage A choices as a fraction of total
observations (Bayesian probabilities in parenthesis) |
| Evidence | Well-rested | Total Sleep
Deprivation |
|
Green | Red | PA=.33 | PA=.50 | PA=.67 | PA=.33 | PA=.50 | PA=.67 |
| 0 | 6 | -- (.04) | -- (.08) | -- (.15) | -- (.04) | -- (.08) | -- (.15) |
| 1 | 5 | 0/6 (.08) | 0/3 (.15) | -- (.26) | 1/6 (.08) | 1/5 (.15) | 0/3 (.26) |
| 2 | 4 | 0/7 (.15) | 0/9 (.26) | 1/2 (.41) | 1/5 (.15) | 0/7 (.26) | 4/9 (.41) |
| 3 | 3 | 0/13 (.26) | 3/15 (.41) | 9/13 (.58) | 2/15 (.26) | 1/15(.41) | 6/11 (.58) |
| 4 | 2 | 9/17 (.41) | 10/13 (.58) | 20/21 (.73) | 3/14 (.41) | 8/9 (.58) | 12/14 (.73) |
| 5 | 1 | 3/3 (.58) | 7/7 (.73) | 8/8 (.85) | 3/4 (.58) | 8/9 (.73) | 8/8 (.85) |
| 6 | 0 | -- (.74) | 1/1
(.85) | 5/5 (.92) | 2/2 (.74) | 5/6 (.85) | 2/2 (.92) |
| Cage A=4 Green, 2 Red Balls; Cage B=3 Green, 3 Red Balls. |
The decision model estimates we report account for the potential
non-independence of decisions of a given subject across trials as a
subject-specific random effect, but our results are robust to
error-term specification. Here, as in Grether (1980), we estimate the
following decision model:
|
Yit* = α + β1 ln LR(A)t + β2 ln
| ⎛
⎜
⎜
⎝ | | | | ⎞
⎟
⎟
⎠ | |
+ µi + εit
(1) |
where Yit* is the subject
i’s subjective log odds in favor of Cage A in trial t,
LR(A)t is the likelihood ratio (evidence) for Cage A,
and ( PA/1−PA ) is the prior odds ratio for Cage
A. The dichotomous variable Yit is observed
equal to 1 if Yit* ≥ 0, and so
we estimate (1) using a random effects probit technique. Grether
(1980) estimates logit results for this model, without accounting for
subject-specific random effects, and so our econometric specifications
are similar but not identical. The Bayes rule hypothesis is that
α=0, and
β1 = β2 > 0, while
overweighting the evidence implies
β1 > β2 ≥ 0.
Grether (1980) found that, for most groups, subjects overweight the
evidence relative to the prior odds.
To evaluate the effects of sleep deprivation (SD), we estimate the
decision model with a dummy variable SD=0,1 and interaction terms
allowing for SD-specific effects on either prior odds and/or new
evidence weighting. Specifically, we estimate:
|
| | Yit* = α + β1 ln LR(A)t + β2 ln
| ⎛
⎜
⎜
⎝ | | | | ⎞
⎟
⎟
⎠ | |
|
| | | |
| + β3 · SDit + β4 (ln LR(A)t · SDit)
| | | |
| + β5 | ⎛
⎜
⎜
⎝ | ln | ⎛
⎜
⎜
⎝ | | | | ⎞
⎟
⎟
⎠ | · SDit
| ⎞
⎟
⎟
⎠ | + µi + εit
|
| | | (2) |
|
And finally, to evaluate the potential learning confound, we estimate a
model similar to (2) for the control data, except with a dummy variable
and interaction terms to account for the second administration of the
task. That is, the control subject model estimated is:
|
| |
Yit* = α + β1 ln LR(A)t + β2 ln
| ⎛
⎜
⎜
⎝ | | | | ⎞
⎟
⎟
⎠ | |
|
| | | |
| + β3 · 2ndAdminit
+ β4 (ln LR(A)t · 2ndAdmit)
| | | |
| + β5 | ⎛
⎜
⎜
⎝ | ln | ⎛
⎜
⎜
⎝ | | | | ⎞
⎟
⎟
⎠ | · 2ndAdminit
| ⎞
⎟
⎟
⎠ | + µi + εit
|
| | | (3) |
|
| Table 2: Probit estimates of Yit* models
(1), (2), and (3) (random effects specification. p-values given in parenthesis). |
| | Model (1)
Main data
(N=288) | Model (2)
Main data
(N=288) | Model (3)
Control subjects
(N=144) |
|
Coefficient estimated | Coeff. | marg.
effect | Coeff. | marg.
Effect | Coeff. | Marg.
Effect |
| Constant | 0.03
(.83) | 0.01
(.83) | 0.14
(.61) | 0.051
(.61) | –0.01
(.97) | –0.004
(.96) |
β1
(evidence) | 1.27
(.00)*** | 0.48
(.00)*** | 2.41
(.00)*** | 0.90
(.00)*** | 1.40
(.00)*** | 0.55
(.00)*** |
β2
(prior odds) | 1.10
(.00)*** | 0.42
(.00)*** | 1.53
(.00)*** | 0.57
(.00)*** | 1.51
(.00)*** | 0.60
(.00)*** |
β3
(SD/2nd day) | -- | -- | –0.21
(.48) | –0.08
(.48) | –0.77
(.30) | –0.30
(.30) |
β4
(SD/2nd
day*evidence) | -- | -- | –1.43
(.00)*** | –0.53
(.00)*** | 0.69
(.22) | 0.27
(.22) |
β5
(SD/2nd day*prior odds) | -- | -- | –0.59
(.24) | –0.22
(.24) | 0.03
(.96) | 0.01
(.97) |
% correctly predicted
by model | 84.38% | 84.38% | 85.42% |
The estimation results of models (1), (2), and (3), are shown in Table
2, and the models are all reasonably accurate at predicting subject
choices. The consistency across models is that both prior odds and
new evidence are significant predictors of Cage A choice. Model (1)
is most similar to the Grether (1980) estimations8, though the tendency in the
pooled data (i.e., both well-rested and sleep-deprived sessions) to
overweight the evidence is not statistically significant.9 Model (2) offers just one way to estimate the
effects of sleep deprivation on the decision weight placed on prior
odds versus new evidence, but our results are robust to different
estimation approaches.
The estimation of model (2) highlights the key result that, following
sleep loss, the decision weight placed on the new evidence is
significantly reduced (see cells in boldface). The results from Model (3)
do not show a similar effect of the second-day session in the control
subjects, thus indicating that our key result is not caused by
learning or ordering of the tasks. We arrive at the same basic
conclusion if we directly test this by pooling all data (i.e.,
experimental and control data) and including dummy variables and
interactions terms to examine whether our key main finding is robust.
To do this, we create a dummy variable for Control subjects
and for the Session (=1 for second session). Note that
Session=1 and Control=0 implies a sleep-deprived
subject, and estimate the following model:
|
| | Yit* = α + β1 ln LR(A)t + β2 ln
| ⎛
⎜
⎜
⎝ | | | | ⎞
⎟
⎟
⎠ | |
|
|
| |
| | | + β3 Session
+ β4 Control
+ β5 (ln LR(A)t · Session)
| |
| | | + β6 (ln LR(A)t · Control)
+ β7 (Session · Control)
| |
| | | + β8 (ln LR(A)t · Session · Control)
+ µi + εit
| (4) |
|
| Table 3: Summary results from pooled data (experimental and
Control). |
| Parameter | α | β1 | β2 | β3 | β4 | β5 | β6 | β7 | β8 |
| Marginal effect | 0.05 | 0.84 | 0.48 | –0.07 | –0.05 | –0.46 | –0.34 | –0.07 | 0.73 |
| p-value (two-tailed test) | 0.61 | 0.00 | 0.00 | 0.51 | 0.78 | 0.01 | 0.04 | 0.64 | 0.02 |
As can be seen in Table 3 results, both the evidence and the prior odds
matter in the expected way, with subjects overweighting the evidence
(p=.01 for the χ2 test of
β1 = β2) in making their
Cage A choice. Control subjects weight the evidence less than the main
experiment subjects (β6 < 0). Most
importantly, the interaction between lnLR(A)*Session*Control)
indicates that control subject increase the weight they place
on the evidence in the second session
(β8 > 0). Because the general
tendency is to reduce weight on the evidence in the second session
(β5 < 0), this indicates a fundamental
difference in the second session effect for Control subjects versus
main experiment subjects (for whom session two means
“sleep-deprived”). In fact, these
results indicate there may be a general trend to increase the weight
placed on evidence when one repeats the task a day later, but sleep
loss reverses that tendency. This supports our claim that the
reduction in estimated decision weight on new evidence following sleep
deprivation in Table 2 is not driven by the ordering of our
treatments.
Our second result is quite intriguing. Though the estimated decision
model significantly differs following sleep loss, choice accuracy is
maintained. Whether well-rested or sleep-deprived, subjects indicated
the correct cage 67–68% of the time.10 To the extent that relevant new information is
valuable, our Model (2) results in Table 2 indicate that accuracy
might be expected to drop, in general, following sleep deprivation
because the decision-weight on new evidence falls. However,
well-rested subjects were overweighting the new evidence relative to
efficient Bayesian updating (i.e., β1 > β2 in Model 2,
p=.03). Thus, the altered decision process following sleep
deprivation reduces (non-Bayesian) hyper-focus on new
information — this should, ceteris paribus, increase choice
accuracy. That choice accuracy is not altered following total sleep
deprivation may result from our simple dichotomous choice environment,
and is therefore not a general result. A more sensitive outcome
measure, such as probability estimates, may highlight interesting
effects masked in our design. Nevertheless, our design recreates a
dichotomous choice environment that is similar to many real-world
environments where choice is among two courses of action.
Actual choice accuracy may be biased if the more likely Cage, based on
Bayesian updated probabilities, is often not the actual Cage (just by
random chance). However, further examination of subject choices
indicate that they coincide with the more likely Bayesian event 85%
and 84% of the time when subjects are well-rested and sleep-deprived,
respectively.11 We also note that our
second result (i.e., maintained choice accuracy following sleep loss)
implies equal accuracy only in assessing the likelihood of being in
state A versus state B. In many cases, an individual cannot choose the
decision environment, and so it is important to note that our results
do not imply that all decisions, in general, are resilient to
short-term sleep loss.
4 Discussion
Our results are significant in today’s modern
sleep-deprived society. Existing research has not thoroughly examined
the effects of sleep deprivation on decision-making, and the present
results on Bayesian updating suggest certain components of
decision-making are resilient to at least some level of sleep loss.
That is, we find no evidence that roughly 24 hours of total sleep
deprivation affects the quality of final choices in this binary choice
environment, and these results do not appear to mask important
individual subject differences in the data.12
Of course, decision accuracy in this environment may deteriorate with
longer bouts of sleep deprivation, but more extended periods of sleep
loss would have less external relevance. For example, Van Dongen et
al., (2003) show that some of the effects of 24 hours of sleep
deprivation are replicated when subjects get 4–6 hours of sleep per
night for up to a week (i.e., partial but chronic sleep deprivation),
which may reflect more typical sleep loss. Decision quality may also
suffer under more complex tasks, but caution must be exercised in any
more complex task design so as to not confound the pure task of
probability updating with other decision-making dimensions (e.g.,
short-term memory). Because total sleep deprivation has been shown to
impair functioning in other areas (e.g., short-term memory, reaction
time, motor function), our evidence suggests that the empirical data on
increased accidents/errors due to sleep loss are not necessarily
attributable to reduced abilities to integrate multiple pieces of
information into a decision. This argues for additional research to
more thoroughly examine this surprising finding.
Our experiment involves an unavoidable risky decision environment.
Emerging evidence indicates that sleep deprivation may lead individuals
to select, on average, more risky decision environments (McKenna et
al., 2007). Though we find error rates to be unaffected by
sleep deprivation (in our simple task), the cost of each error may be
higher in a riskier scenario. In our related research, individuals
seem desensitized to risk following approximately 24 hours of total
sleep deprivation (McKenna et al., 2007), with preferences converging
towards risk neutrality in both the payoff gains and loss domains.
This has interesting implications for, among others, military personnel
choosing to engage or not engage in a riskier outcome scenario, or a
physician choosing between two courses of surgical action.
The finding of significant differences in estimated decision models for
well-rested versus sleep-deprived subjects also merits further
exploration. Our results are consistent with recent research that has
found that underlying cognitive processes may be quite different
following sleep deprivation even though task performance is unaffected
(Drummond et al., 2000; Venkatraman et al., 2007). As such, the change
in estimated decision model we find may be a first clue to the types of
decision-related cognitive processes altered following sleep loss. For
example, if the trend to decrease the weight placed on the evidence
continues with longer bouts of sleep deprivation, this might suggest
that individuals are eventually unable to integrate multiple pieces of
information into a decision, instead relying on only a single variable
and/or a stereo-typed response.
One might hypothesize that subjects run up against the constraints of
bounded rationality following sleep deprivation, thus forcing a change
in their methods of inference. For example, Gigerenzer and Goldstein
(1996) showed that simplistic models of inference need not do worse
than more complex algorithms. In may merely be a coincidence in our
data that the estimated decision model following sleep deprivation
appears Bayesian (i.e., equal weighting of prior odds and evidence).
For example, subjects appear to place less weight on both evidence
and prior odds following sleep deprivation, except that the
estimated effect on prior odds is smaller in magnitude not
statistically significant (p=.24, see Model (2) in Table 2). This may
indicate that what appears Bayesian may actually be an artifact of
subjects weighting all sources of information to (varied) lesser
degrees following sleep loss. While our studied was not designed to
discriminate between use of simple heuristics, it would be useful to
explore heuristics further in a distinct sleep study.
Decreased flexibility in responding to external stimuli during sleep
deprivation has been reported by other authors (Harrison and Horne,
1998 and 1999). A possible related explanation for our results might
be that subjects put less effort into calculating the actual
probability of a given outcome during sleep deprivation and instead
rely on approximating the answer (Drummond et al., 1999). This could
be similar to verbatim decisions and gist decisions in Fuzzy Trace
Theory (Reynanerd, 1991) and would be consistent with the finding of
less weight being placed on both the prior odds and the sample evidence
in the decision model following sleep deprivation. Finally, the
effects of sleep deprivation reported here may result more from an
impairment in the ability to integrate information during sleep loss,
rather than specifically related to decision making per se. While the
process of integrating information has not been well studied during
sleep deprivation, several studies report deficits in the ability to
maintain and manipulate information in working memory during sleep
deprivation (Bartel et al., 2004; Chee et al., 2006; Malemed and
Oksenberg, 2002; Smith et al., 2002; Turner et al., 2007), and this
would be expected to impair one’s ability to integrate
multiple sources of information during decisions.
Evidence from behavioral neuroscience studies indicate that biological
processes are altered following sleep deprivation. For example,
Drummond et al. (2000) studied behavioral and neural outcomes in free
recall memory tasks. Though behavioral outcomes showed no significant
change, neural responses following sleep deprivation were significantly
different. Such results are consistent with a hypothesis of
“compensatory recruitment”,
whereby distinct brain regions may be recruited to compensate for the
adverse condition of sleep loss. Others have reported similar
increases in brain activation and intact performance during sleep
deprivation on a variety of tasks (Drummond et al, 2001, 2004, 2005;
Portas et al, 1998; Chee & Choo, 2004), and Stricker et al (2006) have
reported changes in the neural networks that perform a given task after
sleep deprivation. Hsu et al., (2005) examined decision-making under
uncertainty in a neuroeconomics experiment, and they suggest a
multi-regional neural system for evaluating uncertainty.
Though we examine only behavioral outcomes in this paper, the evidence
we find may be a clue indicating neural activation differences in
information-updating environments. For example, the ventrolateral
prefrontal cortex (VLPC) has been implicated in the neural process of
integrating new contingencies (Paulus, et al, 2004) while the
dorsolateral prefrontal cortex (DLPFC) plays a major role in
integrating multiple pieces of information (Cabeza & Nyberg, 2000;
Cohen et al, 1997). Thus, we might hypothesize decreased activation of
the VLPC and/or DLPFC following sleep deprivation. Existing sleep
research suggests that compensatory activation may occur in the
parietal lobes following sleep loss, thus maintaining performance
(e.g., Drummond et al., 2000, 2001, 2005). While this is suggestive,
further research is certainly necessary, because it highlights that our
understanding of judgments and decision-making following sleep
deprivation is incomplete at best.
References
Akerstedt, T., Fredlund, P., Gillberg, M., & Jansson, B. (2002). A
prospective study of fatal occupational accidents -- relationship to
sleeping difficulties and occupational factors. Journal of
Sleep Research, 11, 69–71.
Bartel, P., Offermeier, W., Smith, F., & Becker, P. (2004). Attention
and working memory in resident anesthetists after night duty: group
and individual effects. Occupational and Environmental
Medicine, 61, 167–70.
Belenky, G., Wesensten, N. J., Thorn, D. R., Thomas, M. L., Sing, H. C.,
Redmond, D. P., Russo, M. B., & Balkin, T.J.. (2003). Patterns of
performance degradation and restoration during sleep restriction and
subsequent recovery: A sleep dose-response study. Journal of
Sleep Research, 12, 1–12.
Biddle, J. E., & Hamermesh, D. S. (1990). Sleep and the allocation of
time. Journal of Political Economy, 98, 922–43.
Cabeza, R. & Nyberg, L. (2000). Imaging cognition II: An empirical
review of 275 PET and fMRI studies. Journal of Cognitive
Neuroscience, 12, 1–47.
Chee, M. W. L., & Choo, W. C. (2004). Functional imaging of working
memory after 24 hr of total sleep deprivation. Journal of
Neuroscience, 24, 4560–4567.
Chee, M. W. L., Chuah, Y. M. L., Venkatraman, V., Chan, W. Y., Philip,
P., & Dinges, D. (2006). Functional imaging of working memory
following normal sleep and after 24 and 35 h of sleep deprivation:
Correlations of fronto-parietal activiation with performance.
NeuroImage, 31, 419–28.
Cohen, J. D., Perlstein, W. M., Braver, T. S., Nystrom, L. E., Noll, D.
C., Jonides, J. & Smith, E. E. (1997). Temporal dynamics of brain
activation during a working memory task. Nature, 386,
604–8.
Coren, S. (1996). Sleep Thieves. New York: Free Press.
Drake, C. L., Roehrs, T., Richardson, G., Walsh, J. K., & Roth, T.
(2004). Shift work sleep disorder: Prevalence and consequences beyond
that of symptomatic day workers. Sleep, 27, 1453–62.
Drummond, S. P. A., Brown, G. G., Gillin, J. C., Stricker, J. L., Wong,
E. C., & Buxton, R. B. (2000). Altered brain response to verbal
learning following sleep deprivation. Nature, 403,
655–57.
Drummond, S. P. A., Brown, G. G., Salamat, J. S., & Gillin, J. C.
(2004). Increasing task difficulty facilitates the cerebral
compensatory response to total sleep deprivation. Sleep,
27, 445–51.
Drummond, S. P. A., Brown, G. G., Stricker, J. L., Buxton, R. B., Wong,
E. C., & Gillin, J. C. (1999). Sleep deprivation-induced reduction
in cortical functional response to serial subtraction.
Neuroreport, 10, 3745–48.
Drummond, S. P. A., Meloy, M. J., Yanagi, M. A., Orff, H. J., & Brown,
G. G. (2005). Compensatory recruitment after sleep deprivation and
the relationship with performance. Psychiatry Research:
Neuroimaging, 140, 211–23
Drummond, S. P. A., Gillin, J. C., & Brown, G. G. (2001). Increased
cerebral response during a divided attention task following sleep
deprivation. Journal of Sleep Research, 10. 85–92.
Friedl, K. E., Mallis, M. M., Ahlers, S. T., Popkin, S. M., & Larkin,
W. (2004). Research requirements for operational decision-making using
models of fatigue and performance. Aviation Space &
Environmental Medicine, 75, A192–9.
Gigerenzer, G., & Goldstein, D. G. (1996). Reasoning the fast and
frugal way: Models of bounded rationality. Psychological
Review, 103, 650–69.
Goldman, L. T., McDonough, M. T., & Rosemond, G. P. (1972). Stresses
affecting surgical performance and learning. Journal of
Surgical Research, 12, 83–86.
Grether, D. M. (1980). Bayes Rule as a descriptive model: The
representativeness heuristic. Quarterly Journal of Economics,
95, 537–557.
Grether, D. M. (1992). Testing Bayes rule and the representativeness
heuristic: Some experimental evidence. Journal of Economic
Behavior and Organization, 17, 31–57.
Griffin, D., & Tversky, A. (1992). The Weighing of evidence and the
determinants of confidence. Cognitive Psychology, 24, 411–35.
Harrison, Y., & Horne, J. A. (2000). The impact of sleep deprivation
on decision making: A review. Journal of Experimental
Psychology: Applied, 6, 236–49.
Harrison, Y., & Horne, J. A. (1999). One night of sleep loss impairs
innovative thinking and flexible decision making.
Organizational Behavior and Human Decision Processes,
78, 128–45.
Harrison, Y., & Horne, J. A. (1997). Sleep deprivation affects
speech. Sleep, 20, 871–77.
Harrison, Y., & Horne, J. A. (1998). Sleep loss impairs short and
novel language tasks having a prefrontal focus. Journal of
Sleep Research, 7, 95–100.
Hsu, M., Bhatt, M., Adolphs, R., Tranel, D., & Camerer, C. F. (2005).
Neural Systems responding to degrees of uncertainty in human
decision-making. Science, 310, 1680–83.
Johnson, L. C., & Spinweber, C. L. (1983). Good and poor sleepers
differ in Navy performance. Military Medicine, 148,
727–31.
Kamstra, M. J., Kramer, L. A., & Levi, M. D. (2000). Losing Sleep at
the Market: The daylight saving anomaly. American Economic
Review, 90, 1005–11.
Killgore, W. D., Balkan, T. J., & Wesensten, N. J. (2006). Impaired
decision making following 49 h of sleep deprivation. Journal
of Sleep Research, 15, 7–13.
Kuppermann, M., Lubeck, D. P., Mazonson, P. D., Patrick, D. L.,
Steward, A. L., Buesching, D. P., & Fifer, S. K. (1995). Sleep
problems and their correlates in a working population.
Journal of General Internal Medicine, 10, 25–32.
Leger, D. (1994). The cost of sleep-related accidents: A report for
the National Commission on Sleep Disorders Research. Sleep,
17, 84–93.
McElroy, T., & Seta, J. J. (2003). Framing effects: An
analytic-holistic perspective. Journal of Experimental Social
Psychology, 39, 610–17.
McKenna, B., Dickinson, D. L., Orff, H., & Drummond, S. P. A. (2007).
The effects of one-night of sleep deprivation on known-risk and
ambiguous-risk decisions. Journal of Sleep Research,
16, 245–52.
Melamed, S., & Oksenberg, A. (2002). Excessive daytime sleepiness and
risk of occupational injuries in non-shift daytime workers.
Sleep, 25, 315–22.
Paulus, M. P., Feinstein, J. S., Tapert, S. F., & Liu, T. T. (2004).
Trend detection via temporal difference model predicts inferior
prefrontal cortex activiation during acquisition of advantageous action
selection. Neuroimage, 21, 733–43.
Philibert, I. (2005). Sleep loss and performance in residents and
nonphysicians: a meta-analytic examination. Sleep,
28, 1392–402.
Phillips, B., Magan, L., Gerhardstein, C. & Cecil, B. (1991). Shift work,
sleep quality, and worker health: A study of police officers. Southern
Medical Journal, 84, 1176–1184, 1196.
Pilcher, J. J. & Huffcutt, A. I. (1996). Effects of sleep deprivation
on performance: A meta-analysis. Sleep, 19, 318–26.
Portas, C. M., Rees, G., Howseman, A. M., Josephs, O., Turner, R., &
Frith, C. D. (1998). A specific role for the thalamus in mediating
the interaction of attention and arousal in humans. Journal of
Neuroscience, 18, 8979–89.
Reynanerd, C. J. (1991). Fuzzy-trace theory and
children’s acquisition of scientific and mathematical
concept. Learning and Individual Differences, 3, 27–60.
Smith, M. E., McEvoy, L. K., & Gevins, A. (2002). The impact of
moderate sleep loss on neurophysiological signals during working-memory
task performance. Sleep, 25, 784–94.
Stoller, M. K. (1997). The socio-economics of insomnia: The materials
and methods. European Psychiatry, 12, 41s-48s.
Stricker, J. L., Brown, G. G., Wetherell, L. A., & Drummond, S. P. A.
(2006). The impact of sleep deprivation and task difficulty on
networks of FMRI brain response. Journal of the International
Neuropsychological Society, 12, 591–7.
Van Dongen, H. P. A., Maislin, G., Mullington, J. M., & Dinges, D. F.
(2003). The cumulative cost of additional wakefulness: Dose-response
effects on neurobehavioral functions and sleep physiology from chronic
sleep restriction and total sleep deprivation. Sleep,
26, 117–26.
Venkatraman V., Chuah, Y. M. L., & Huettel, S. A. (2007). Sleep
deprivation elevates expectation of gains and attenuates response to
losses following risky decisions. Sleep, 30, 603–9
Turner, T. H., Brown, G. G., Drummond, S. P. A., & Salamat, J. S.
(2007). Total sleep deprivation’s effects on component
processes of verbal working memory. Neuropsychology, 21,
787–95.
Weinger, M. B., & Ancoli-Israel, S. (2002). Sleep deprivation and
clinical performance. Journal of the American Medical
Association, 287, 955–7.
This document was translated from LATEX by
HEVEA.
