Judgment and Decision Making, Vol. 12, No. 6, November 2017, pp. 563-571
Between me and we: The importance of self-profit versus social justifiability for ethical decision making
Sina A. Klein*
Isabel Thielmann#
Benjamin E. Hilbig# $
Ingo ZettlerX
|
Current theories of dishonest behavior suggest that both individual
profits and the availability of justifications drive
cheating. Although some evidence hints that cheating behavior is
most prevalent when both self-profit and social justifications are
present, the relative impact of each of these factors is
insufficiently understood. This study provides a fine-grained
analysis of the trade-off between self-profit versus social
justifiability. In a non-student online sample, we assessed
dishonest behavior in a coin-tossing task, involving six conditions
which systematically varied both self-profit and social
justifiability (in terms of social welfare), such that a decrease in
the former was associated with the exact same increase in the
latter. Results showed that self-profit outweighed social
justifiability, but that there was also an effect of social
justifications.
Keywords: dishonest behavior; cheating; social justification; self-profit; social welfare
1 Introduction
Dishonest behavior is prevalent in various everyday situations, ranging
from private context (e.g., cheating in romantic relationships),
semi-public settings (e.g., tax evasion), to large public crises (e.g.,
cheating on pollution emissions tests). Corresponding to this
significance of dishonesty for inter-individual relations and society
at large, research on the determinants of dishonest behavior has
recently seen an upsurge of interest, most prominently in the field of
behavioral ethics (Bazerman & Gino, 2012; Gino & Shalvi, 2015; Mazar,
Amir & Ariely, 2008), which studies dishonesty in the form of cheating
behavior – that is, misreporting facts in order to increase gains (most
typically, monetary payoffs).
Generally speaking, dishonesty yields potential individual benefits
that likely drive the high prevalence of dishonest behavior. Indeed,
recent evidence suggests that a substantial proportion of individuals
take potential gains into account and become more willing to lie as
incentives increase (Hilbig & Thielmann, 2017). However, dishonesty
may also incur costs: First, potential punishment or sanctions may
result in external costs for the cheater (Becker, 1968).
Moreover, psychological approaches to dishonesty emphasize that
cheating may also incur internal (i.e., psychological) costs,
namely, a threat to individuals’ positive self-image (Mazar et al.,
2008). The possibility of cheating thus creates a dilemma in which
self-profit and the motivation to maintain a positive self-image
conflict. In turn, individuals are assumed to engage in
ethical maneuvering (Shalvi, Handgraaf & de Dreu, 2011) to
find a compromise between the desire to make a profit and the desire
to be an honest person.
A prominent strategy to maintain a positive self-view in the face of
dishonest behavior is the use of so-called self-serving
justifications which may reduce the internal costs of cheating by
“providing reasons for questionable behaviors and making them appear
less unethical” (Shalvi, Gino, Barkan & Ayal, 2015, p. 125). Indeed,
prior research shows that cheating typically increases if self-serving
justifications are available as, for instance, in ambiguous situations.
Specifically, when cheating was attributable to an “unintentional”
mistake such as a confusion of payoff-relevant die rolls that had been
produced or even merely observed (Bassarek et al., 2017, Shalvi, Dana,
Handgraaf & de Dreu, 2011), participants were more likely to cheat than if such
attribution was impossible. The same was found for choices in an
ambiguous cheating paradigm in which higher ambiguity led to a higher
willingness to lie (Pittarello, Leib, Gordon-Hecker & Shalvi, 2015).
In addition to ambiguous situations, feelings of entitlement and
deserving have been found to increase cheating (Poon, Chen & DeWall,
2013; Schindler & Pfattheicher, 2017), most plausibly because they are
likewise used to justify cheating. Finally, people seem to avoid major
lies (i.e., lies that necessitate a large distortion of facts) because
they are less easily justifiable than more minor ones (Hilbig &
Hessler, 2013, Shalvi, Handgraaf, et al., 2011).
Another way to justify cheating applies to situations in which other
individuals will additionally benefit from one’s dishonesty (so-called
self-serving altruism; e.g., Shalvi et al., 2015). In such
situations providing a social justification, cheating has
been found to substantially increase. For instance, in a set of
studies, participants’ payoff for the number of allegedly solved tasks
was either given to the participant herself (pro-self
cheating), split between her and another participant
(self-other cheating), or entirely given to another
participant (other-only cheating) (Gino, Ayal & Ariely,
2013; Wiltermuth, 2011). Participants cheated significantly more when
cheating incurred a personal benefit and was socially
justifiable (i.e., self-other cheating) than when either self-profit
or social justifications were present (i.e., pro-self or other-only
cheating; for similar findings see also Biziou-van-Pol, Haenen,
Novaro, Liberman & Capraro, 2015). The authors concluded that
individuals care about both self-profit and justifications in their
decision to behave dishonestly. Interestingly, no meaningful
differences in cheating rates were apparent between the pro-self and
other-only conditions (Gino et al. 2013; Wiltermuth, 2011). In a
similar vein, individuals lied less in a deception game for their own
profit when their lie implied concurrent costs for another individual
(Erat & Gneezy, 2012; Gneezy, 2005), most plausibly because this
reduces one’s justification for lying.
Taken together, extant evidence suggests that the conjoint presence of
self-profit and social justifications – in terms of benefits for
others – increases dishonesty and outweighs the effect of self-profit
and social justifications alone. However, the relative importance of
self-profit versus social justifiability for cheating behavior remains
unclear. Specifically, previous studies (e.g., Gino et al., 2013;
Wiltermuth, 2011) typically implemented self-other cheating in a way
that provided the exact same extent of self-profit and social
justifiability1 for
dishonest behavior (e.g., 1€ for the cheating individual and 1€ for
another individual).
To allow for a more fine-grained analysis of the importance
individuals place to self-profit versus social justification, we
compared individuals’ willingness to cheat across different conditions
in which we systematically increased individuals’ self-profit while
simultaneously decreasing the strength of (social) justifiability of
cheating. More specifically, we implemented six cheating conditions,
each of which was characterized by a pre-defined ratio of how a
monetary gain was split between the cheater herself and another
unknown participant. That is, a decrease in self-profit from one
condition to the next was associated with the exact same increase in
social justifiability, manipulated in terms of an increase in
absolute social welfare defined as the sum of payoffs. By
implication, the end points of this gradual design were pro-self
cheating (i.e., high self-profit but no social justification) and
social welfare maximizing cheating (i.e., high strength of social
justification but no self-profit). Overall, the experimental design
thus allowed for a direct and straightforward test of the relative
importance of self-profit versus social justifiability in a decision
to cheat.
2 Method
| Table 1: Overview of self- and other-profit as well as resulting social welfare
in the six cheating conditions. |
| Condition | Self-profit | Other-profit | Social welfare |
| 1 (other-only) | 0€ | 5€ x 2 =10€ | 10€ |
| 2 | 1€ | 4€ x 2 = 8€ | 9€ |
| 3 | 2€ | 3€ x 2 = 6€ | 8€ |
| 4 | 3€ | 2€ x 2 = 4€ | 7€ |
| 5 | 4€ | 1€ x 2 = 2€ | 6€ |
| 6 (pro-self) | 5€ | 0€ x 2 = 0€ | 5€ |
2.1 Measures and design
To assess dishonest behavior, we relied on a commonly used cheating
paradigm that implements a probabilistic link between participants’
reports and actual cheating (Fischbacher & Föllmi-Heusi, 2013;
Moshagen, Hilbig, Erdfelder & Moritz, 2014; Shalvi, Dana et al.,
2011; Shalvi, Handgraaf et al., 2011). Specifically, we used the
following coin-tossing task (Hilbig & Zettler, 2015): Participants
take a coin, are informed about the target side (i.e., heads or
tails), and toss the coin in private for a specified number of times
(in our case twice). Their task is to simply report whether a certain
number of successes (the coin turning up target side) was obtained,
which is associated with certain payoffs. Clearly, participants can
misreport the number of successes (or even not toss a coin at all)
while anonymity is fully preserved since it is impossible to determine
the actual outcomes of the coin tosses of any one
individual. Nonetheless, since the probability of a certain number of
successes in a certain number of tosses can be directly calculated
from the binomial distribution, the actual probability of dishonesty
(i.e., participants reporting the payoff-maximizing number of
successes irrespective of the actual successes obtained) can be
estimated (Moshagen & Hilbig, 2017).
As sketched above, the experiment implemented a within-subjects design
with six conditions, which were presented to participants in
counterbalanced order. In each condition, participants tossed the coin
twice and generated 5€ (approximately 5.34 US$ at the time of data
collection) if they reported having obtained two successes in exactly
two tosses (the baseline probability of this to occur assuming full
honesty is 25%). The 5€ were then split in a pre-specified ratio
(which varied across conditions) between the participant herself and
another participant. The crucial manipulation was how the 5€ would be
split: As shown in Table 1, self-profit increased in 1€-steps across
the six conditions whereas social welfare (the absolute sum of
payoffs) decreased in 1€-steps. To achieve the manipulation of social
welfare, the share for the other participant was always doubled by the
experimenter (much like in a public goods game or similar social
dilemmas; e.g., Kollock, 1998). For instance, condition 3 specified a
split of 2€ for the participant herself and 3€ for the other unknown
person. The latter amount was doubled, resulting in a 6€ payoff for
the other and thus a total social welfare of 2€ + 6€ = 8€. In
condition 4, by comparison, the split was 3€ for the cheater and 2€
for the other unknown person, resulting in a social welfare of 3€ +
2*2€ = 7€. Consequently, there is a 1€ increase in self-profit and a
1€ decrease in social welfare from condition 3 to 4. Notably, in the
end point conditions 1 and 6, either self-profit (pro-self cheating)
or social justifications (other-only cheating) were given but not
both. These end-point conditions thus make the current study
comparable to previous studies that mostly used pro-self and/or
other-only cheating. In addition, the inclusion of other-only cheating
allowed us to specifically test whether there is an additive effect of
social justifications beyond self-profit, meaning that cheating also
occurs if only profiting another person. (Instructions, materials, and
data are available through the journal’s table of
contents.)
Importantly, depending on the relative importance of self-profit and
social justifiability, cheating rates should differ in systematic ways
across the six conditions: If self-profit is the predominant driver of
dishonesty, cheating rates should increase with self-profit, despite
the corresponding decrease in social justifiability (i.e., loss in
social welfare). If, in turn, social justifiability is the predominant
driver of dishonesty, cheating rates should increase with social
justifiability, despite the corresponding decrease in
self-profit. Finally, if self-profit and social justifiability are of
comparable importance such that they compensate for each other,
cheating rates should be highly similar across conditions.
2.2 Procedure and participants
The experiment was conducted as a web-based study via
Bilendi, a professional panel provider in
Germany. Participants first provided informed consent and demographic
information. Next, they completed a personality
questionnaire2 not pertinent
to this investigation, before receiving detailed instructions on the
coin-tossing task. That is, participants were told that they were
going to complete six trials of the same task that differed only with
regard to how the to-be-generated 5€ is split between themselves and a
randomly selected other participant. Participants were informed that
the other participant was another unknown person (also participating
in the study) in each trial and that one trial would ultimately be
selected at random to determine their own and the other’s payoffs. In
each trial, participants then received information about the self- and
other-profit at stake, and were also provided with a randomly
determined target side for the coin toss (determined anew in each
trial). Participants were instructed to take a coin, to toss it twice,
and to report whether the target side occurred twice in exactly two
tosses. Correspondingly, the response options were “Yes, the coin
turned up target side in both tosses” and “No, the coin did not turn
up target side in both tosses”. Participants were aware that nobody
would be able to observe their tosses and that the outcome depended
entirely on whether they reported having obtained two
successes. If participants indicated that the target side occurred
twice, they generated 5€ that were split between themselves and
another randomly chosen participant as specified in the specific
trial. If participants indicated that the target side did not occur
twice, no payoff was generated in the specific trial at hand and the
5€ remained in the experimental budget. Once participants had
completed the six coin-toss trials, we selected one trial at random
and informed participants about their own and the other’s payoff
resulting from their own response in this particular trial.
| Table 2: Observed proportion of “yes”-responses, associated estimate of
the probability of dishonesty (95% confidence intervals of this
estimate in parentheses), and test of the latter probability against 0
(i.e., whether cheating occurred), separately per condition |
.
| Condition | Observed proportion of “yes”-responses | Probability of dishonesty d | Test of d against 0 |
| 1 (other-only) | .36 | .15 [.06; .24] | Δ G2(1) = 12.92, p < .001, Cohen’s
ω = .10 |
| 2 | .36 | .15 [.06; .24] | Δ G2(1) = 12.92, p < .001,
Cohen’s ω = .10 |
| 3 | .44 | .26 [.17; .35] | Δ G2(1) = 36.80, p < .001,
Cohen’s ω = .17 |
| 4 | .45 | .26 [.17; .35] | Δ G2(1) = 38.55, p < .001.
Cohen’s ω = .17 |
| 5 | .51 | .35 [.26; .44] | Δ G2(1) = 67.18, p < .001,
Cohen’s ω = .23 |
| 6 (pro-self) | .44 | .25 [.16; .34] | Δ G2(1) = 35.08, p < .001,
Cohen’s ω = .17 |
After data collection, participants received their payment consisting
of a flat fee, the additional payout from their own coin toss (if
any), and (if applicable) the additional payout from another’s coin
toss (M = 2.93€ in addition to the flat fee). Payment was
entirely handled by the recruiting panel provider, who was blind to
the specific task at hand, thus further increasing anonymity of
participants. Of note, conducting the study online via a professional
panel provider allowed us to recruit a particularly diverse sample
(N = 2103). That is, participants were virtually equally
distributed across the sexes (51.2% female) and spanned a broad age
range from 19 to 67 years (M = 39.9, SD = 12.7). The
majority of participants (70.5%) were employed, only 9.5% were
students.
3 Results
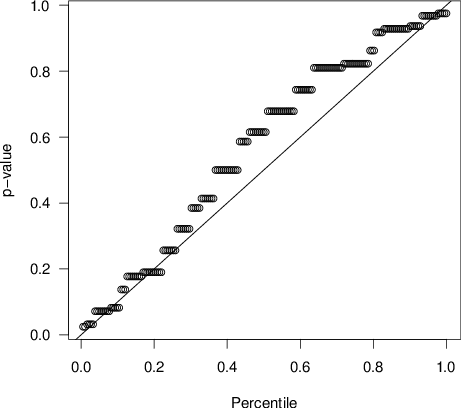
| Figure 1: Distribution of one-tailed p-values of
inter-correlations (Kendall’s τ ) between responses (1 = “yes”, 0
= “no”) in the coin-tossing task and experimental condition per
participant (n = 182, as 28 participants gave the same
responses in all conditions and could thus not be included in this
analysis). |
Table 2 reports the observed proportion of “yes”-responses per
condition. As can be seen, the proportion of “yes”-responses was within
the typical range found in these types of paradigms, that is,
consistently above the baseline probability of winning (.25), but not
substantially more than twice as large. However, since there is
necessarily a non-zero chance of two actual successes in two tosses,
the observed rate of “yes”-responses conflates cheating and legitimate
wins. Thus, for each condition we additionally calculated an estimate
of the rate of cheating by
where p("yes") denotes the observed proportion of
“yes”-responses and p denotes the baseline probability of
winning (.25) (for formal details, see Moshagen & Hilbig, 2017). The
estimated probability of dishonesty ( d), which is
equivalent to the proportion of dishonest participants in the present
design, was consistently larger than 0 and smaller than .40. As is
apparent in Table 2, all likelihood-ratio tests testing the probability
of dishonesty against 0 for each condition were significant, thus
confirming that cheating occurred in all conditions.
Next, we tested whether and how dishonesty differed across conditions.
As can be seen descriptively in Table 2, the probability of dishonesty
tended to increase across conditions. To analyze this potential effect
of condition on cheating behavior, we analyzed “yes”-responses per
individual per condition using a multi-level logistic regression as
implemented in the glmer function of the lme4 package (Bates,
Maechler, Bolker & Walker, 2015) in R (R Core Team, 2017).4
Specifically, we included a subject-level random intercept and
specified the experimental condition as fixed linear effect to predict
“yes”-responses (coded as 1, “no”-responses as 0). Mirroring the
descriptive pattern summarized in Table 2 – and implying that cheating
indeed increased with increasing self-profit – results showed a
significant positive effect of condition on the probability to respond
“yes”, B = .11, SE = .04, p = .001. Notably, adding
a random slope to the model to account for potential individual
variation in the effect of condition on “yes”-responses did not
improve model fit, χ2(df = 2) = 0.03, p =
.986. This implies that, overall, individuals were similarly
responsive to changes in self-profit versus social justifiability,
meaning that there was a general tendency to become more likely to
cheat the higher the self-profit.
The conclusion that individuals were generally more likely to
cheat with increasing self-profit was also supported by the
distribution of p-values for the individual-level
correlation between responses and conditions. Specifically, we
calculated the one-tailed p-value for Kendall’s τ
between responses (1 = “yes”, 0 = “no”) and condition (1–6) for each
individual and plotted the resulting p-values against their
percentile rank (Figure 1; for details on this procedure, see Baron,
2010). Each point in the plot represents the p-value of one
single participant for the hypothesis that “yes”-responses become less
likely from condition 1 (other-only cheating) to condition 6 (pro-self
cheating). If there is no relation between the variables of interest
(here: responses and condition), all p-values should
roughly fall on the diagonal which implies a uniform (random)
distribution. Apparently, however, the p-values
systematically deviated from the diagonal, clustering above the
diagonal in the upper right part of the plot. This implies that
if participants reacted to the experimental manipulation of
self-profit versus social welfare, their willingness to respond “yes”
increased with increasing self-profit, confirming the general
preference for self-interest over social justifiability on the
individual level. In turn, essentially no participant showed a clear
preference for social welfare and thus for social justifiability over
self-profit, as indicated by the absence of systematic deviation from
the diagonal in the lower left part of Figure 1.5
Finally, as is apparent in Table 2, there was one notable exception to
the trend of an increasing probability of dishonesty with increasing
self-profit. Specifically, dishonesty was not largest in condition 6
incorporating self-profit only (i.e., pro-self cheating): Once social
justifiability was absent (i.e., social welfare dropped to zero), the
estimated probability of dishonesty again decreased. To test whether
this decrease was significant, we conducted an analysis using the same
random-intercept regression model from above but adding a dummy
variable contrasting the pro-self cheating condition 6 (codes as 1)
against the remaining conditions 1–5 involving some degree of social
justifiability (coded as 0). Confirming that cheating indeed decreased
once social justifiability was completely absent, the dummy variable
yielded a significant negative effect on “yes”-responses, B =
−.50, SE = .22, p = .022, whereas the general positive
trend of increasing probability of “yes”-responses with higher
self-profit still remained significant, B = .19, SE = .05,
p < .001. This implies that cheating consistently
increased with increasing self-profit but only as long as cheating was
still somehow justifiable.
4 Discussion
Dishonest behavior is highly prevalent in everyday life, arguably
because it yields noteworthy profits for the cheating individual.
However, since cheating also appears to bear costs such as posing a
threat to one’s moral self-image (Mazar et al., 2008), individuals are
assumed to seek justifications that render dishonest behavior
subjectively less severe. For instance, whenever cheating incurs a
profit for others in addition to oneself, individuals are more willing
to cheat because cheating is socially justifiable (Shalvi et al.,
2015). However, it is unclear just how self-profit affects
cheating vis-à-vis social justifiability. To close this gap, the
present experiment investigated the relative impact of both
determinants using a gradual design in which self-profit and social
justifiability (in terms of social welfare) were inversely related.
Specifically, across six conditions using a coin-tossing task, the
strength of social justifications decreased to the exact same extent as
self-profit increased, with the end point conditions of this design
implementing either pure other-profit or pure self-profit.
Overall, our results imply that cheating occurred in each condition,
but to a notably different extent across conditions. Specifically,
cheating increased with increasing self-profit and decreasing strength
of social justifications. This shows that self-profit is the primary
driver of dishonesty, suggesting that individuals place more
importance on what they personally gain from cheating than on what is
gained in total (in terms of social welfare). Nonetheless, cheating
also occurred in the other-only condition in which only social
justifiability was present whereas self-profit was zero. Also, once
social justifiability was absent (social welfare dropped to zero),
cheating decreased (despite the further increase in
self-profit). Taken together, these findings demonstrate an effect of
social justifiability beyond self-profits: Justifications alone
suffice to produce some cheating, and cheating is clearly fostered if
social justifications are available in addition to self-profit.
Notably, the present results are highly compatible with previous
studies investigating cheating behavior. First, the rate of dishonesty
in the pure pro-self condition 6 (d = .25) is perfectly
consistent with the mean rate of dishonesty found across many studies
using similar paradigms (median estimate of d across studies
= .24; Hilbig & Hessler, 2013; Hilbig, Moshagen & Zettler, 2016;
Hilbig & Zettler, 2015; Moshagen et al., 2014; Thielmann, Hilbig,
Zettler & Mosagen, 2017; Zettler, Hilbig, Moshagen & de Vries, 2015;
see also Abeler, Nosenzo & Raynold, 2016, for a recent
meta-analysis). Second, a significant rate of dishonesty in the
other-only condition corresponds to findings showing that people cheat
not only to profit themselves but also (and exclusively) to profit
others (Erat & Gneezy, 2012). This – as well as the significant
cheating rates in the remaining conditions 2, 3, and 4 in which
other-profit exceeded self-profit – once again indicates that
participants are even willing to cheat if this result in larger
benefits for another and thus makes the participant relatively worse
off. By implication, individuals seem to care more about their
absolute self-profit than about direct social comparison to another
individual. Finally, evidence shows that cheating rates typically peak
in the joint presence of self-profit and social justifications (Gino
et al. 2013; Wiltermuth, 2011), especially when self-profits are
relatively high (Erat & Gneezy, 2012). In our experiment, the highest
probability of dishonesty (d5 = .35)
also occurred when both social justifications and self-profit were
present – specifically, when self-profit was highest but social
justifiability was still given.
Although our study extends prior findings in providing first evidence
on the relative impact of self-profit and social justifiability for
dishonesty to occur, future research might investigate whether
self-profit outweighs social justifications in
general. First, social justifications could become more important
than self-profit when they are manipulated in another way than via
social welfare. For instance, previous research shows that cheating
for the benefit of another is especially prevalent when the other is a
person in need, a finding that has been referred to as the
robin-hood-effect (Gino & Pierce, 2010a, 2010b). This
implies that dishonesty for the mere benefit of another might be
higher than observed in the present study when the beneficiary is
needier than the cheating individual herself. A gradual design as the
one used in our experiment with the beneficiary being a needy person
(with varying need) instead of some random other participant might
thus provide further insight into the relative importance of
self-profit and social justifications.
Second, we cannot rule out that social justifiability might be more
important than self-profit for other groups of participants stemming
from different societies or cultures, respectively, and/or being
recruited in a different way. The sample in our study consisted of
people registered in a panel for participating in online studies. One
could argue that the main goal of participating in these studies is to
make money. Thus, the fact that self-profit outweighed social
justifiability might be specific for such sample types. Although (i)
our findings are overall compatible with much previous evidence using
other samples and (ii) not a single participant of our sample actually
appeared to place more weight on social justifications than on
self-profit, future research should investigate the possibility that
the relative weight assigned to self-profit and social justifiability
might depend on characteristics of the specific sample or other
moderators such as culture, personality, or whether losses rather than
gains are at stake (Erat & Gneezy, 2012; Gneezy, 2005; Schindler &
Pfattheicher, 2017).
In conclusion, the present work contributes to the understanding of the
relative influence of self-profit versus social justifiability on
people’s decision to cheat. Our data suggests that self-profit is the
primary driver of cheating behavior – whereas profits for others have
an additive, but smaller impact. As such, people seem to care more
about their ultimate gains from cheating than about whether their
dishonesty is socially justifiable.
References
Abeler, J., Nosenzo, D., & Raymond, C. (2016). Preferences for
truth-telling. CeDEx Discussion Paper 2016-13, Center for
Decision Research & Experimental Economics.
Ashton, M. C., & Lee, K. (2009). The HEXACO-60: A short measure of the
major dimensions of personality. Journal of Personality
Assessment, 91(4), 340–345. https://doi.org/10.1080/00223890902935878.
Bassarek, C., Leib, M., Mischkowski, D., Strang, S., Glöckner, A., & Shalvi, S. (2017). What provides justification for cheating – producing
or observing counterfactuals? Journal of Behavioral Decision
Making, 30(4), 964–975. http://dx.doi.org/ 10.1002/bdm.2013
Batchelder, W. H., & Riefer, D. M. (1999). Theoretical and empirical
review of multinomial process tree modeling. Psychonomic
Bulletin & Review, 6, 57–86. http://dx.doi.org/10.3758/BF03210812.
Baron, J. (2009). Looking at individual subjects in research on judgment
and decision making (or anything). Acta Psychologica Sinica,
42, 1–11.
Bates, D., Maechler, M., Bolker, B., & Walker, S. (2015). Fitting
linear mixed-effects models using lme4. Journal of Statistical
Software, 67(1), 1–48. http://dx.doi.org/10.18637/jss.v067.i01.
Bazerman, M. H., & Gino, F. (2012). Behavioral ethics: Toward a
deeper understanding of moral judgment and dishonesty. Annual
Review of Law and Social Science. (8),
85–104. http://dx.doi.org/10.1146/annurev-lawsocsci-102811-173815.
Becker, G. S. (1968). Crime and punishment: An economic approach.
Journal of Political Economy, 76(2),
169–217. http://dx.doi.org/10.1086/259394.
Biziou-van-Pol, L., Haenen, J., Novaro, A., Liberman, A. O., & Capraro,
V. (2015). Does telling white lies signal pro-social preferences?
Judgment and Decision Making, 10(6), 538–548.
Erat, S., & Gneezy, U. (2012). White Lies. Management Science,
58(4), 723–733. http://dx.doi.org/10.1287/mnsc.1110.1449.
Erdfelder, E., Auer, T.-S., Hilbig, B. E., Aßfalg, A., Moshagen, M.,
& Nadarevic, L. (2009). Multinomial processing tree models.
Zeitschrift für Psychologie - Journal of Psychology,
217(3),
108–124. http://dx.doi.org/10.1027/0044-3409.217.3.108.
Fischbacher, U., & Föllmi-Heusi, F. (2013). Lies in disguise - An
experimental study on cheating. Journal of the European
Economic Association, 11(3), 525–547. http://dx.doi.org/10.1111/jeea.12014.
Gino, F., Ayal, S., & Ariely, D. (2013). Self-serving altruism? The
lure of unethical actions that benefit others. Journal of
Economic Behavior & Organization, 93,
285–292. http://dx.doi.org/10.1016/j.jebo.2013.04.005
Gino, F., & Pierce, L. (2010a). Robin Hood under the hood: Wealth-based
discrimination in illicit customer help. Organization Science,
21(6), 1176–1194. http://dx.doi.org/ 10.1287/orsc.1090.0498.
Gino, F., & Pierce, L. (2010b). Lying to level the playing field: Why
people may dishonestly help or hurt others to create equity.
Journal of Business Ethics, 95, 89–103.
http://dx.doi.org/10.1007/s10551-011-0792-2.
Gino, F., & Shalvi, S. (2015). Editorial overview: Morality and ethics:
New directions in the study of morality and ethics. Current
Opinion in Psychology, 6, v-viii.
http://dx.doi.org/10.1016/j.copsyc.2015.11.001.
Gneezy, U. (2005). Deception: The role of consequences. The
American Economic Review, 95(1), 384–395. http://dx.doi.org/10.1257/0002828053828662.
Grünwald, P. D. (2007). The minimum description length
principle. Cambridge, MA: MIT Press.
Heck, D. W., Moshagen, M., & Erdfelder, E. (2014). Model selection by
minimum description length: Lower-bound sample sizes for the Fisher
information approximation. Journal of Mathematical Psychology,
60, 29–34. http://dx.doi.org/10.1016/j.jmp.2014.06.002.
Heck, D. W., Wagenmakers, E.-J., & Morey, R. D. (2015). Testing order
constraints: Qualitative differences between Bayes factors and
normalized maximum likelihood. Statistics & Probability
Letters, 105, 157–162. http://dx.doi.org/10.1016/j.spl.2015.06.014.
Hilbig, B. E., & Hessler, C. M. (2013). What lies beneath: How the
distance between truth and lie drives dishonesty. Journal of
Experimental Social Psychology, 49(2), 263–266.
http://dx.doi.org/10.1016/j.jesp.2012.11.010.
Hilbig, B. E., Moshagen, M., & Zettler, I. (2016). Prediction consistency:
A test of the equivalence assumption across different indicators of the
same construct. European Journal of Personality, 30, 637–647.
http://dx.doi.org/10.1002/per.2085.
Hilbig, B. E. & Thielmann, I. (2017). Does everyone have a price? On
the role of payoff magnitude for ethical decision making.
Cognition, 163, 15–25. http://dx.doi.org/ 10.1016/j.cognition.2017.02.011.
Hilbig, B. E., & Zettler, I. (2015). When the cat’s away, some mice
will play: A basic trait account of dishonest behavior. Journal
of Research in Personality, 57, 72–88.
http://dx.doi.org/10.1016/j.jrp.2015.04.003.
Kollock, P. (1998). Social dilemmas: The anatomy of cooperation.
Annual Review of Sociology, 24,
183–214. http://dx.doi.org/10.1146/annurev.soc.24.1.183.
Knapp, B. R., & Batchelder, W. H. (2004). Representing parametric order
constraints in multi-trial applications of multinomial processing tree
models. Journal of Mathematical Psychology, 48,
215–229. http://dx.doi.org/ 10.1016/j.jmp.2004.03.002.
Mazar, N., Amir, O., & Ariely, D. (2008). The dishonesty of honest
people: A theory of self-concept maintenance. Journal of
Marketing Research, 45(6), 633–644. http://dx.doi.org/10.1509/jmkr.45.6.633.
Moshagen, M. (2010). multiTree: A computer program for the analysis of
multinomial processing tree models. Behavior Research Methods,
42(1), 42–54. http://dx.doi.org/ 10.3758/BRM.42.1.42.
Moshagen, M., & Hilbig, B. E. (2017) The statistical analysis of
cheating paradigms. Behavior Research Methods, 49,
724–732. http://dx.doi.org/ 10.3758/s13428-016-0729-x.
Moshagen, M., Hilbig, B. E., & Zettler, I. (2014). Faktorenstruktur,
psychometrische Eigenschaften und Messinvarianz der deutschsprachigen
Version des 60-Item HEXACO Persönlichkeitsinventars. Diagnostica,
60(2), 86–97.https://doi.org/10.1026/0012-1924/a000112.
Moshagen, M., Hilbig, B. E., Erdfelder, E., & Moritz, A. (2014). An
experimental validation method for questioning techniques that assess
sensitive issues. Experimental Psychology, 61(1),
48–54. http://dx.doi.org/10.1027/1618-3169/a000226.
Myung, J. I. (2000). The importance of complexity in model selection.
Journal of Mathematical Psychology, 44(1), 190–204.
http://dx.doi.org/10.1006/jmps.1999.1283.
Myung, J. I., Navarro, D. J., & Pitt, M. A. (2006). Model selection by
normalized maximum likelihood. Journal of Mathematical
Psychology, 50(2), 167–179. http://dx.doi.org/ 10.1016/j.jmp.2005.06.008.
Pittarello, A., Leib, M., Gordon-Hecker, T., & Shalvi, S. (2015).
Justifications shape ethical blind spots. Psychological
Science, 26(6), 794–804. http://dx.doi.org/10.1177/0956797615571018.
Poon, K. T., Chen, Z., & DeWall, C. N. (2013). Feeling entitled to more
ostracism increases dishonest behavior. Personality and Social
Psychology Bulletin, 39, 1227–1239.
R Core Team (2017). R: A Language and Environment for
Statistical Computing. Vienna, Austria: R Foundation for Statistical
Computing. https://www.R-project.org/.
Rissanen, J. J. (1996). Fisher information and stochastic complexity.
IEEE Transactions on Information Theory, 42, 40–47.
Schindler, S., & Pfattheicher, S. (2017). The frame of the game:
Loss-framing increases dishonest behavior. Journal of
Experimental Social Psychology, 69, 172–177.
Shalvi, S., Gino, F., Barkan, R., & Ayal, S. (2015). Self-serving
justifications: Doing wrong and feeling moral. Current
Directions in Psychological Science, 24(2), 125–130.
http://dx.doi.org/10.1177/0963721414553264.
Shalvi, S., Dana, J., Handgraaf, M. J., & de Dreu, C. K. (2011).
Justified ethicality: Observing desired counterfactuals modifies
ethical perceptions and behavior. Organizational Behavior and
Human Decision Processes, 115(2), 181–190.
http://dx.doi.org/10.1016/j.obhdp.2011.02.001.
Shalvi, S., Handgraaf, M. J. J., & de Dreu, C. K. (2011). Ethical
manoeuvring: Why people avoid both major and minor lies.
British Journal of Management, 22, 16–27.
http://dx.doi.org/10.1111/j.1467-8551.2010.00709.x.
Thielmann, I., Hilbig, B. E., Zettler, I., & Moshagen, M. (2017).
On measuring the sixth basic personality dimension: A comparison
between HEXACO Honesty-Humility and Big Six Honesty-Propriety.
Assessment, 24(8), 1024–1036.http://dx.doi.org/10.1177/1073191116638411.
Wiltermuth, S. S. (2011). Cheating more when the spoils are split.
Organizational Behavior and Human Decision Processes,
115(2), 157–168. http://dx.doi.org/10.1016/j.obhdp.2010.10.001.
Wu, H., Myung, J. I., & Batchelder, W. H. (2010). On the minimum
description length complexity of multinomial processing tree models.
Journal of Mathematical Psychology, 54(3), 291–303.
http://dx.doi.org/10.1016/j.jmp.2010.02.001.
Zettler, I., Hilbig, B. E., Moshagen, M. & De Vries, R. (2015).
Dishonest responding or true virtue? A behavioural test of Impression
Management. Personality and Individual Differences, 81,
107–111.
Appendix
Given that the observed rate of “yes”-responses in the coin-tossing
task conflates cheating and legitimate wins, corresponding effect
sizes are necessarily underestimated (Moshagen & Hilbig, 2017). The
analysis reported in this appendix relies directly on the estimated
probability of dishonesty. Analyses were conducted within the
multinomial processing tree model framework (Batchelder & Riefer,
1999; Erdfelder et al., 2009) using the multiTree software (Moshagen,
2010). The model estimating the probability of dishonesty (per
condition) comprises two parameters: The first, d, is the
probability of dishonesty (of an individual respondent in this
situation). Dishonest respondents answer “yes” irrespective of the
outcome of the coin-tossing task. If one is honest (probability
1−d), the response depends on the outcome of the coin-tossing task:
In case of two successes (which occurs with probability p), one
responds “yes”, otherwise (probability 1−p) “no”. The value of p
(which represents the second parameter in the model) is known from the
binomial distribution (.25 in our paradigm) and thus fixed to this
value in all analyses. For the entire experiment, the full (baseline)
model comprises six such trees (one per condition) with distinct free
parameters representing the probability of dishonesty (i.e.,
d1−6) and a single p-parameter fixed to .25 across all
conditions. The full model equations and corresponding raw data file
can be found through the journal’s table of
contents.
Corresponding to data analyses within the multinomial processing tree
framework, our original sample size considerations were based on an a
priori power analysis within this framework using multiTree (Moshagen,
2010). Specifically, we determined the sample size required to detect
differences in the rate of dishonesty (with assumend dishonesty rates
increasing in equal step sizes from 0 in the other-only condition to
0.3 in the pro-self condition) across conditions (tested against a
model assuming that dishonesty is constant across conditions) with high
power of 1−β = .95 at α = .05. The power analysis
yielded a required sample size of N = 142 per condition and
thus N = 852 observations in total, which we considered a
lower-bound estimate. Notably, the required sample size also clearly
exceeds the minimum-N required for the model comparisons
reported below which is N = 45 (Heck, Moshagen & Erdfelder,
2014). We recruited N = 210 participants who completed the
study, generating 1260 observations in total.
Corresponding to our main research question whether cheating differs
as a function of self-profit versus social justifications, we first
analyzed whether all d-parameters can be constrained to equality
(i.e., d1 = d2= d3= d4= d5= d6) which is
implied by the hypothesis that self-profit and social justifications
are equally important. This model fitted significantly worse than the
baseline model allowing all d-parameters to vary freely
(Δ G2 = 14.53, p = .013), thus corroborating that
the probability of dishonesty indeed differed across conditions. The
corresponding effect size of Cohen’s ω = .11 indicated a small
overall difference between conditions.
To further test whether these differences across cheating conditions
were systematic in nature (i.e., showing an upward or downward trend
from condition 1 to 6) – as implied by the analyses on the
“yes”-responses (see main text) – we compared two specific models,
namely model (A) implying that dishonesty increases across conditions
(i.e., d1 < d2 < d3 < d4 < d5 < d6) and thus that
self-profit outweighs social justifications versus model (B) implying
that dishonesty decreases across conditions (i.e.,
d1 > d2 > d3 > d4 > d5 > d6) and thus that social
justifications outweigh self-profit. Note that the mere
larger/smaller-relations are particularly appropriate in the present
case as they also allow for non-linear trends which is important given
that there is no way to judge by how much subjective self-profits let
alone justifications vary across conditions. In addition, the
comparison included an unconstrained model (C) with all
d-parameters varying freely. The two models representing the
possible trends involve parametric order constraints which are easily
implemented in the multinomial processing tree framework through
reparameterizing the model (Knapp & Batchelder, 2004).
For comparison of these non-nested models involving order constraints,
we relied on a criterion based on the minimum description length
principle (Grünwald, 2007; Myung, 2000; Myung, Navarro, & Pitt,
2006). Note that the non-nested nature of the models and the
inclusion of order constraints ruled out use of the likelihood-ratio
test as well as reliance on information criteria such as AIC or BIC
which ignore functional complexity (Myung et al., 2006).
The minimum description length of a model is the sum of
goodness-of-fit and a model complexity term. In the case of
multinomial models, the latter can be defined as the sum of the
maximum likelihoods of all possible data vectors from the outcome
space. An approximation to the complexity term is the Fisher
Information Approximation (cFIA; Rissanen, 1996; Wu, Myung &
Batchelder, 2010) which is obtained by a Monte Carlo algorithm in
multiTree as used here. The corresponding FIA weights (Heck,
Wagenmakers, & Morey, 2015) revealed that model (A) involving the
restriction d1 < d2 < d3 < d4 < d5 < d6 was clearly
superior with a posterior probability of .99. Thus, in summary, the
model comparison clearly corroborated the results from the multi-level
regression analyses predicting “yes”-responses: Dishonesty increased
with increasing self-profit and decreasing social justifications.
This document was translated from LATEX by
HEVEA.
