
| Figure 1: Screenshot of decisions-to-engage paradigm in Study 1. In the decisions-from-feedback condition, “Observe” was replaced with “0 pts for sure”. In Study 2 the “Option” labels were replaced with each option’s outcome and its probability. |
Judgment and Decision Making, Vol. 12, No. 6, November 2017, pp. 553-562
‘Tis better to choose and lose than to never choose at allNathaniel J. S. Ashby* # Tim Rakow$ Eldad Yechiam$ |
When decisions involve opting in or out of competition many decision makers will opt-in even when doing so leads to losses on average. In the current paper, we examine the generality of this effect in risky choices not involving competition. We found that re-framing a sure (certain) zero option as an option to observe the results of the other options without choosing would lead to increased consequential choice (i.e., increased selection of risky options rather than the zero option). Specifically, in two studies we compared the rate of consequential choice in a novel paradigm where decision makers decide to observe or to choose with consequence from a set of risky options (decisions-to-engage) to a full-feedback decisions-from-feedback paradigm where the choice set included a labeled sure zero option. Compared to decisions-from-feedback, participants were more likely to choose from mixed (risky) gambles with consequence (over a zero outcome) in decisions-to-engage. This occurred irrespective of whether doing so was advantageous (i.e., when choice led to monetary gains on average) or disadvantageous (i.e., when choice led to monetary losses on average), and when descriptions of the options outcomes and probabilities were provided (Study 2). These findings provide an important boundary condition for the positive effects of experience on the quality of choice, and suggest that decision makers’ preference for agency can sometimes induce poorer choices.
Keywords: loss aversion, loss avoidance, decisions-from-experience,
decision making, decision strategy, agency.
Recent work suggests that increased experience with a pair of options (i.e., making choices and receiving outcome feedback) increases the rate of selecting options that return higher average rewards in risky choice, that is, choices that maximize expected value (EV: Ashby & Gonzalez, 2017; Konstantinidis, Ashby & Gonzalez, 2015; Yechiam & Hochman, 2013). This increased maximization with increasing experience is observed both when options provide net gains or losses on average (Ashby & Rakow, 2016, 2017), and, under some conditions, such experiential choice has been found to outperform choice based on a description of probabilities and outcomes (Jessup, Bishara & Busemeyer, 2008).1 In addition, most participants appear to employ strategies that maximize EV, and in addition endorse strategies aimed at EV maximization (Ashby, Konstatinous & Yechiam, 2017), although, in some situations, participants use strategies that maximize value in the short run (Wulff, Hills & Hertwig, 2015). Furthermore, experience appears to reduce biases that can lead to divergence from EV maximization such as loss aversion and avoidance (e.g., Erev, Ert & Roth, 2010; Erev, Gilat-Yihyie, Marchiori & Sonsino, 2015; Erev, Ert & Yechiam, 2008; Yechiam & Hochman, 2013; but see, Abdellaoui, L’Haridon & Paraschiv, 2011; Glöckner, Hilbig, Henniger & Fiedler, 2016, for negative results).
Most studies involving decisions-from-experience have employed paradigms like decisions-from-feedback (Barron & Erev, 2003) or decisions-from-samples (Hertwig, Barron, Erev & Weber, 2004). In decisions-from-feedback (also referred to as the clicking paradigm), decision makers are forced to make repeated choices between options with unknown outcomes and probabilities; thus, decision makers learn about the outcomes and their probabilities only by making consequential choices. In decisions-from-samples (also referred to as the sampling paradigm), decision makers sample (simulate playing options at no monetary cost) from available options before making one forced consequential choice. As noted, in both tasks decision makers are forced to make a choice between the options presented to them (as, indeed, is the case in most laboratory experiments on decision making). However, many everyday choices are part of an inter-connected chain of decisions, in which a choice between options is predicated on a prior decision of whether or not to pick one of the available options. For example, we must decide if we want to invest in the stock market, play the lottery, attend an academic conference, buy a home, or go on a vacation before we ever consider which stock, lottery-game, talk, home, or vacation destination we prefer.2 Thus, the studies that have found that experience frequently leads to increases in EV maximization have not captured what may be an important nuance of many, if not most, decisions made outside the lab (for an exception, see Erev et al., 2010).
Table 1: Sets of non-zero options and their outcomes (O1 & O2) in points, probabilities (P1 & P2), and expected values (EV1 & EV2). Points were converted at a rate of 30 points to a $0.01. The first column indicates which sets were used in each study.
Option 1 Option 2 Study Set type O11 P11 O12 P12 EV1 O21 P21 O22 P22 EV2 1 & 2 Gain only 53 0.33 27 0.67 36 75 0.33 9 0.67 31 1 & 2 Mixed +EV 53 0.33 −13 0.67 9 75 0.33 −31 0.67 4 1 & 2 Mixed –EV 28 0.33 −53 0.67 −26 50 0.33 −71 0.67 −31 2 Gain only 43 0.4 28 0.6 34 85 0.4 8 0.6 39 2 Mixed +EV 43 0.4 −12 0.6 10 85 0.4 −32 0.6 15 2 Mixed –EV 18 0.4 −0.52 0.6 −24 6 0.4 −72 0.6 −19

Figure 1: Screenshot of decisions-to-engage paradigm in Study 1. In the decisions-from-feedback condition, “Observe” was replaced with “0 pts for sure”. In Study 2 the “Option” labels were replaced with each option’s outcome and its probability.
In the current study, we examine the effect of how the decision is presented by including or excluding the dilemma of whether to choose or not. (For a similar design involving insurance purchases see Szrek & Baron, 2007.) Specifically, we contrast a condition framed as a forced choice between options (one of which is known to always pay zero), with a condition in which the sure zero option is framed as an opportunity to opt out of the choice by taking a passive observational role. In both conditions, participants learn the final outcome of all options. One domain where such a framing difference is expected to have an effect is in decisions where all options return net losses on average. For example, participants in Erev et al. (2010) decided whether to play a competitive game with another player. They reported a strong tendency to play the game even if it involved large losses and smaller gains. One explanation for this oddity is that it reflects a general tendency to take risks (for small amounts of money) in repeated choices independently of the framing of the decision. Another explanation is that participants derived some value from competition (Franken & Brown, 1995).
To clarify this potential impact of decision framing we examine situations where one can “exclude” oneself from playing by deciding to observe without consequence (e.g., in order to gather information) and where no direct competition is involved (i.e., “games against nature”).3 In Study 1 we examined whether re-framing an option paying 0 with certainty (as in a standard decision-from-feedback task) as an “observe” option (our decisions-to-engage task) increases the selection of (other) available options, including those producing losses on average. Study 2 replicates and extends Study 1 by including descriptions of the options outcomes and probabilities and including a greater variety of choice sets. Our hypothesis is that, when given the option of opting in or out of consequential choice, decision makers will be more likely to choose from options with consequences rather than receiving nothing with certainty. Thus, we test whether decision makers are less likely to choose a sure zero option when it is framed as not acting (i.e., observing).
Both studies employed two paradigms: (1) a novel task combining the decisions-from-feedback (Barron & Erev, 2003) and decisions-from-samples (Hertwig et al., 2004) paradigms that we call the decision-to-engage paradigm; and (2) a version of the decisions-from-feedback paradigm (Barron & Erev, 2003). In each study, participants were randomly assigned to one of these two paradigms (conditions).
In the decisions-to-engage condition, participants were informed that they would face several tasks in which they would make 100 decisions between alphabetically-labeled options (e.g., “Option A”, “Option B”, shown in Figure 1). Table 1 shows the sets of options in each study. In addition, they were informed that they could instead choose to observe by pressing an option labeled “observe”. When participants opted to observe (i.e., clicked the observe button) they were shown the outcomes that occurred for all available options (i.e., what they would have won or lost had they chosen with consequence). If they choose with consequence they saw the outcome that occurred for the option they selected, as well as what they would have won or lost had they instead selected the other option. Thus, full feedback was available for all options irrespective of the choice they made. The decisions-from-feedback condition was identical to the decisions-to-engage condition except the observe option was labeled “0 pts. with certainty”. Thus, in the decisions-to-engage condition, selecting the sure zero option was framed as taking an inactive/passive role, while in the decisions-from-feedback it was framed as an active choice of receiving nothing.
Table 2: Participant details and pay.
Study N N Decisions-from-Experience N Decisions-to-Engage % male Mage Pay received 1 207 103 104 50% 34.4 $0.75 + choice-contingent pay (∼$1) 2 231 121 110 47% 36.2 $1.50 + choice-contingent pay (∼$2)
In both studies, irrespective of condition, outcomes remained on the screen until a participant made the next decision; decisions for a given choice set concluded after 100 decisions; participants encountered all choice sets in random order; and participants were told when they had finished their choices for each choice set and that a new set of choices would follow. Participants were under no time constraints when making their decisions.
As indicated in Table 1 some (non-zero) choice sets consisted of only gains (positive outcomes), while others consisted of both gains and losses (mixed outcomes). In half of the mixed outcome sets, all options had positive EVs (+EV; i.e., consequential choice led to gains on average), while, in the other half of the mixed outcome sets, all non-zero options had negative EVs (–EV: i.e., consequential choice led to losses on average). Study 1 used one gain only, one mixed +EV, and one mixed –EV option-set while Study 2 included two of each. All sets included an EV maximizing option: The safer option was always better in Study 1 while the safer and riskier options were better with equal frequency across sets in Study 2. Options were randomly assigned to buttons (labels) at the start of each task.
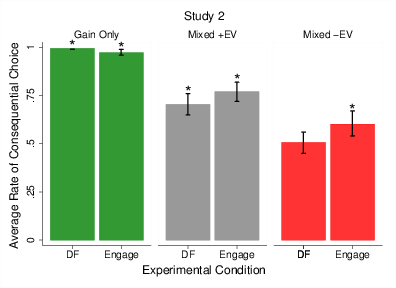
Figure 2: Proportion of participants making consequential choices in Study 1 (top) and Study 2 (bottom): for options with positive outcomes only (left panel); options with mixed outcomes with a positive EV (+EV; middle panel); and options with mixed outcomes with a negative EV (–EV; right panel); by condition: decisions-from-feedback (DF) and decisions-to-engage (Engage). Asterisks indicate that the rate of consequential choice was greater than 50%. Error bars indicate 95% confidence intervals.
Both studies were conducted on Amazon Mechanical Turk. Study 1 preceded another study and lasted 20 minutes on average while Study 2 was run alone and lasted 30 minutes on average. To ensure that participants took their decisions seriously all consequential decisions a participant made were realized.
Table 2 shows the participant characteristics across studies; we aimed for 100 participants per condition in Study 1, while Study 2’s sample size was based on a power analysis aiming to provide high power (1 − β = .90) to detect the difference in choice proportions between the decisions-from-feedback and decisions-to-engage conditions in the mixed negative EV pair, based on the difference observed in Study 1.
Figure 2 (top) displays the proportion of participants choosing with consequence from the gain-only option pair (left panel) and the mixed-outcome option sets providing positive (+EV; middle panel) and negative EVs (–EV; right panel), plotted separately by condition (decisions-from-feedback, DF; decisions-to-engage, Engage).
We compared the rate of consequential choice (choices in each pair averaged by participant) in the decision-to-engage condition to the rate of not choosing the certain zero option in the decision-from-feedback condition using independent t-tests. We found that in the gain-only pair those in the decisions-to-engage condition (95%; CI95%[.93, .98]) did not choose with consequence significantly less than those in the decisions-from-feedback condition (97%; CI95%[.95, .99]), t(205) = .83, p = .41. Nevertheless, in the mixed outcome positive-EV option pair those in the decisions-to-engage condition (66%; CI95%[.59, .72]) chose with consequence more (maximized more) so than those in the decisions-from-feedback condition (53%; CI95%[.47, .59]), t(205) = −2.89, p = .004. Similarly, in the mixed outcome negative-EV option pair those in the decision-to-engage (56%; CI95%[.49, .62]) condition chose with consequence more than those in the decision-from-feedback condition (45%; CI95%[.39, .51]), i.e., maximized EV less, t(205) = −2.49, p = .01.
Figure 3 displays the rate of not choosing the observe or sure zero option (i.e., the rate of consequential choice) over decisions separately for each option-pair and condition. It appears to reflect a decreasing in consequential choice in the decisions-to-engage condition over time in the mixed sets.4 For the final 25 decisions, the decisions-to-engage and decisions-from-feedback conditions did not differ in the gain-only pair, t(205) = .94, p = .35. However, in the mixed positive (t(205) = −2.63, p = .009) and negative EV sets (t(205) = −3.02, p = .003) the rate of consequential choice was higher in the decisions-to-engage condition than in the decisions-from-feedback condition (i.e., experience did not eliminate the effect of frame).
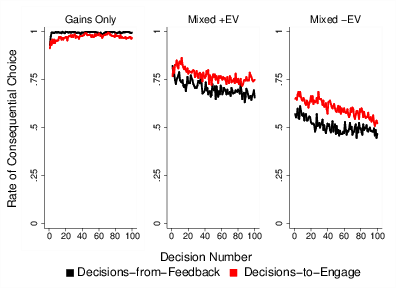
Figure 3: The rate of consequential choice over decisions in Study 1 (top) and Study 2 (bottom), plotted separately for sets containing gains only (Gains Only), mixed outcomes with a positive EV (Mixed +EV), and mixed outcomes with a negative EV (Mixed –EV), and by condition (black = decisions-from-feedback; red = decisions-to-engage).
Study 2 was designed to address two shortcomings of Study 1 and to examine a potential boundary for the observed framing effect. First, due to a programming oversight, foregone outcomes were not recorded in Study 1, precluding potentially informative model fitting. Second, in Study 1 the EV maximizing option was always the safer option. Therefore, in Study 2 three new sets of options were added (one gain only, one mixed +EV, and one mixed –EV) in which the riskier option provided the highest average payout (see Table 1). Study 2 also added descriptive information about each option. Specifically, instead of the options being labeled “Option A” or “Option B” they were labeled with their possible outcomes and the probabilities of those outcomes occurring. Thus, Study 2 allows us to examine whether the effect of framing persists when full information is available: We might, for instance, predict that if participants are explicitly aware that the likelihood and size of a loss occurring is greater than that of a gain they would show a stronger preference for the sure zero option.
Figure 2 (bottom) displays the proportion of participants choosing with consequence from the gain only choice sets (left panel) and the mixed outcome choice sets providing positive (+EV; middle panel) and negative EVs (–EV; right panel), plotted separately by condition (decisions-from-feedback – DF; decisions-to-engage – Engage).
As in Study 1 we compared the rate of consequential choice (choices in each pair type averaged by participant) in the decision-to-engage condition to the rate of not choosing the sure zero option in the standard decision-from-feedback condition. Counter to Study 1 we found that in the gain only choice sets those in the decisions-to-engage condition (97%; CI95%[.96, .99]) chose with consequence slightly, but significantly, less than those in the decisions-from-feedback condition (99%; CI95%[.99, .99]), t(229) = 2.88, p = .004. Those in the decisions-to-engage condition (77%; CI95%[.72, .82]) chose with consequence marginally more than those in the decisions-from-feedback condition (71%; CI95%[.65, .76]) in the mixed outcome positive EV choice sets (i.e., maximized EV more), t(229) = −1.81, p = .07. As in Study 1, those in the decision-to-engage condition (60%; CI95%[.54, .67]) also chose with consequence more than those in the decision-from-feedback condition (51%; CI95%[.45, .56]) in the mixed outcome negative EV choice sets (i.e., maximized EV less), t(229) = −2.19, p = .03.
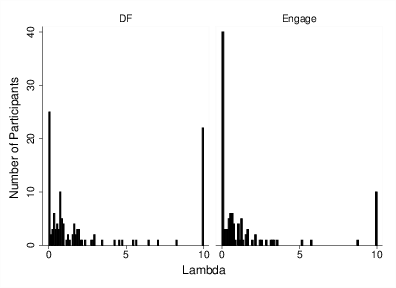
Figure 4: The number of participants estimated as having a given λ (Lambda) by condition: decisions-from-feedback (DF) and decisions-to-engage (Engage).
Figure 3 shows the rate of not choosing the observe or sure zero option (i.e., the rate of consequential choice) over decisions separately for each choice set and condition and appears to show a stronger decline in consequential choice in the mixed sets with experience than observed in Study 1. Focusing on the final 25 decisions between the decisions-to-engage and decisions-from-feedback conditions no differences in significance from those reported above were found for the gain only and mixed outcome positive EV sets. The greater rate of consequential choice in the decisions-to-engage condition was, however, no longer significant in the mixed negative EV choice sets, t(229) = −1.50, p = .13.
Because information about the outcomes and their probabilities of occurrence were provided, the first choice in each pair was roughly equivalent to a decision in a descriptive choice format without feedback. We therefore analyzed whether there was any difference in the rate of consequential choice between the two conditions for these first choices in each set type. No significant differences were found (ts < 1.48, ps > .14).
While the results reported above may suggest that participants were less sensitive to losses in the decisions-to-engage condition, another way to measure aversion to losses is to employ computational modeling to determine how losses are weighted in the decision process. We accomplished this by employing a standard reinforcement learning model including a loss aversion parameter (λ ) which estimates the weighting of losses in the decision process (Ahn, Busemeyer, Wagenmakers & Stout, 2008; see the supplementary analysis in the Appendix for details regarding the model and model fitting). The model was run for the conditions with mixed gains and losses – estimating loss aversion in gain only problems does not make sense. In these conditions if λ is greater than 1 this indicates that losses were weighted more heavily than gains — in line with loss aversion. However, if λ equals 1 this indicates losses and gains were weighted equally, while λ < 1 indicates that losses were weighted less than gains (i.e., the opposite of loss aversion). Figure 4 shows a histogram of these λ by condition. We find that the median value of λ in the standard decisions from experience condition was .88 whereas in the decisions to engage condition it reduced to .52 (Mann-Whitney Z = 3.12, p = .002), suggesting that participants treated losses as if they were less consequential in the decision-to-engage condition. It is notable that the median participant (in either condition) appears to weigh losses less heavily than gains; this is an unusual state of affairs in decision research studies (i.e., losses do not loom larger than gains in our data).
We aimed to determine whether framing a decision as one of taking an active or passive role would increase the rate of selecting sure zero options, even when those options return losses on average. We find that framing the decision as a decision of whether or not to observe increased consequential choice: Participants chose with consequence from mixed outcome options when they provided both positive and negative EVs more than they did in the decisions-from-feedback paradigm and either equal to or greater than chance. While this increase in consequential choice decreased participants’ earnings when options returned net losses on average (i.e., in the mixed outcome negative EV option sets), it increased them when options returned net gains on average (i.e., in the mixed outcome positive EV option sets). In addition, modeling of participants’ decisions suggests that for most participants loss aversion was reversed in both conditions, though to a greater extent in the decision-to-engage paradigm. It seems that when decisions are framed as a decision to opt in or out of taking action participants are less avoidant of potential losses, even when doing so puts them in harm’s way.
These findings add to the literature on loss aversion (the notion that, typically, “losses loom larger than gains”; Kahneman & Tversky, 1979; Tversky & Kahneman, 1991). One logical consequence of loss aversion is that a sure outcome of zero is preferred to a mixed gamble with an EV of zero (Kahneman & Tversky, 1979): This is implied by the steeper relation between outcomes and subjective value for losses compared to gains in the prospect theory value function. Indeed, Tversky and Kahneman (1992) reported that, for the median participant, a mixed outcome positive EV gamble (50/50 gamble between +$202 or –$100) was indicated as being as attractive as a sure outcome of $0. Yet, in our studies, a substantial proportion of participants chose a mixed option with a worse-than-zero EV over a sure zero option even with substantial experience (Studies 1 & 2) and complete knowledge of the outcomes and probabilities (Study 2). Such choices appear counter to loss aversion because a loss averse decision maker would take the sure zero rather than face the risk of losing money (nearly twice as much as they could win in the negative-EV choice sets in Study 1 and some in Study 2)5. Importantly, this adverse tendency is greatest when the decision is framed as a decision-to-engage; thereby adding to the growing literature which shows that sensitivity to losses is in many ways context dependent (e.g., see Yechiam & Hochman, 2013; Walasek & Stewart, 2015).
It is also possible that framing the decisions as a decision-to-engage decreased risk avoidance. In other words, participants might not (only) have underestimated the impact of a loss on their total earnings, but (additionally or alternatively) might have misjudged their relative frequency of occurrence (even when description was provided in Study 2) which would also increase the attractiveness of choosing from the options with consequence, or might simply found the idea of risk taking to be fun. However, if diminished risk aversion of these sorts was the main contributor to the effect, we would also expect to see the rate of playing with consequence to be greater in the decisions-to-engage paradigm than the decisions-from-feedback paradigm in the gain only choice sets as well. This pattern was not observed, and was in fact reversed in Study 2 (although, in both studies, choice with consequences was very close to ceiling). Thus, future studies of this decision-to-engage effect would be wise to select sets of options designed to specifically test how changes in risk sensitivity might contribute to the effect.
One explanation for the current results that fits irrespective of the root cause (decreased loss aversion/avoidance and/or risk avoidance), and can also explain why EV maximization is often observed in decisions-from-feedback, is that in the decision-to-engage paradigm participants developed a myopic focus on the differences in payouts between the two options (Vlaev, Chater, Stewart & Brown, 2011; Stewart, Chater & Brown 2006), rather than the “bigger picture” of the average outcomes actually paid out (Kahneman & Lovallo, 1993; Hills & Hertwig, 2010). Thus, explicitly presenting the options as a two-stage process (a choice to engage, and – if engaging – a choice between options) may mean that decision makers are less likely to compare all options simultaneously. Specifically, participants may have counted the option of not participating as disadvantageous (Wilson et al., 2014). Therefore, consistent with a heuristic such as “you have to be in it to win it”, the mere possibility of gaining something was more rewarding than doing nothing at all, while the size of gains and losses and their frequencies of occurrence played a lesser part in this decision (Wells & Windschitl, 1999; Reyna & Brainerd, 2008). Potentially, this myopic focus emerged in the current setting because participants perceived opting out as losing their agency, which research suggests individuals are averse to (Paternoster & Pogarsky, 2009). This explanation speaks to the seductive ‘grasp’ of the casino, on-line bookmaker, or ‘betting shop’. Once the bettor is drawn into the gambling environment (e.g., by ‘free’ bets, cheap entertainment or cost-effective meals) the choices then encountered there (framed as opt-in decisions) will be more attractive than the equivalent choice encountered in a different context.
Another interesting finding observed in the present studies is that the rate of observational choice increased when losses were possible compared to when they were not: The EVs were also smaller in the mixed outcome sets and outcomes varied more both of which may have played a role. This result seems to be consistent with recent findings in the decisions-from-samples paradigm that participants search more before making a consequential choice if losses are possible (Lejarraga et al., 2012; Lejarraga & Hertwig, 2016; see also Yechiam, Zahavi & Arditi, 2015). More generally, it is consistent with the notion of loss attention (Yechiam & Hochman, 2013), suggesting that losses lead to increased vigilance and scrutiny of the environment. Importantly, though, the current findings indicate that this effect of losses on observational choices was not strong enough to counteract individuals’ tendency to engage in consequential choices that included more frequent losses despite their disadvantageousness.
Our results might seem inconsistent with the “loss attention” account (Yechiam & Hochman, 2013) which predicts increased EV maximization in tasks involving potential losses. Our results show a robust violation of EV maximization both when EVs were positive (choosing without consequence) and negative (choosing with consequence). However, our study did not directly compare EV maximization levels in the different domains, since problems presented in each domain were different in terms of whether the status quo option (observe or 0 option) was advantageous or not (in the gain domain or loss domain, respectively).
A shortcoming of the current work, and of most research exploring decisions-from-experience in the lab, is that decisions outside of the lab rarely happen back to back in a rapid fashion. Similarly, apart from playing state lotteries, casino games, and some forms of investment (and reinvestment), few decisions involve repeated choices from options providing monetary outcomes with fixed probabilities. We would thus urge caution in inferring the generalizability of the current findings to real-world behaviors where decisions are more complex. Nonetheless, our finding that framing a sure zero option as an opt-out option can increase risk-taking (while, conversely, framing an opt-out option as “taking zero” can decrease risk taking) is potentially important. For example, it may speak to the seduction of inducements to gambles that explicitly focus on what may be missed out on by electing not to gamble, and the policy or regulatory decisions about how casinos and bookmakers may advertise their “services”. And there are many situations in which evaluations of products, opportunities, people or situations are based on experiences or observations that are in fact made in rapid succession. Thus, one may consider multiple views of an item, several online reviews of a hotel, or size up a new acquaintance or location based on multiple observations – all acquired in just a few seconds. Moreover, such evaluations are tied to decisions: once observations or experiences have accumulated, one can walk away from the potential purchase, book the hotel, close the door on the salesman, or flee the dark foreboding street. What we learn from laboratory choices that require rapid evaluation of observations may inform our understanding of such situations (e.g., whether “first impressions” weigh heavily in the evaluation and the decision that follows; Ashby & Rakow, 2016; Denrell, 2005).
In sum, the current results provide some insight into the role that experience and choice architecture play in decisions-from-experience. We find that when decisions are framed as a decision to engage or not many decision makers choose to play with consequence irrespective of the possibility and size of potential losses and gains. This increase in consequential choice can be both helpful and harmful depending upon the option payoffs, and therefore provides an important boundary condition for when experience might aid decision makers and when it might lead to self-harm. More generally, our studies point to a gap in the literature. JDM researchers “know” the typical pattern of risk preference under different conditions (e.g., the “four-fold pattern” summarized in textbooks), because there have been hundreds of carefully conducted studies of risky choice. However, almost all of these studies employed forced choice paradigms. Our studies illustrate that the patterns of preference may not look the same when decision makers can choose not to choose and garner some experience (e.g., the fourfold pattern has been shown to be reversed in experiential choice; Hertwig & Erev, 2009). Researching such decisions will give us a fuller understanding of how preferences play out in the decisions where “opting out” is an option.
Abdellaoui, M., L’Haridon, O., & Paraschiv, C. (2011). Experienced vs. described uncertainty: Do we need two prospect theory specifications? Management Science, 57(10), 1879-1895.
Ahn, W. Y., Busemeyer, J. R., Wagenmakers, E. J., & Stout, J. C. (2008). Comparison of decision learning models using the generalization criterion method. Cognitive Science, 32(8), 1376–1402.
Ashby, N. J., Konstantinidis, E., & Yechiam, E. (2017). Choice in experiential learning: True preferences or experimental artifacts? Acta Psychologica, 174, 59–67.
Ashby, N. J., & Rakow, T. (2017). When time is (not) money: Preliminary guidance on the interchangeability of time and money in laboratory-based risk research. Journal of Risk Research, 1–16.
Ashby, N. J., & Rakow, T. (2016). Eyes on the prize? Evidence of diminishing attention to experienced and foregone outcomes in repeated experiential choice. Journal of Behavioral Decision Making, 29(2-3), 183–193.
Barron, G., & Erev, I. (2003). Small feedback-based decisions and their limited correspondence to description-based decisions. Journal of Behavioral Decision Making, 16(3), 215–233.
Denrell, J. (2005). Why most people disapprove of me: Experience sampling in impression formation. Psychological Review, 112, 951–978.
Denrell, J., & March, J. G. (2001). Adaptation as information restriction: The hot stove effect. Organization Science, 12(5), 523–538.
Erev, I., Ert, E., & Roth, A. E. (2010). A choice prediction competition for market entry games: An introduction. Games, 1(2), 117–136.
Erev, I., Gilat-Yihyie, S., Marchiori, D., & Sonsino, D. (2015). On loss aversion, level-1 reasoning, and betting. International Journal of Game Theory, 44(1), 113–133.
Erev, I., Ert, E., & Yechiam, E. (2008). Loss aversion, diminishing sensitivity, and the effect of experience on repeated decisions. Journal of Behavioral Decision Making, 21(5), 575–597.
Ert, E., & Erev, I. (2013). On the descriptive value of loss aversion in decisions under risk: Six clarifications. Judgment and Decision Making, 8(3), 214–235.
Franken, R. E., & Brown, D. J. (1995). Why do people like competition? The motivation for winning, putting forth effort, improving one’s performance, performing well, being instrumental, and expressing forceful/aggressive behavior. Personality and Individual Differences, 19(2), 175–184.
Glöckner, A., Hilbig, B. E., Henninger, F., & Fiedler, S. (2016). The reversed description-experience gap: Disentangling sources of presentation format effects in risky choice. Journal of Experimental Psychology: General, 145(4), 486.
Hertwig, R., Barron, G., Weber, E. U., & Erev, I. (2004). Decisions from experience and the effect of rare events in risky choice. Psychological Science, 15(8), 534–539.
Hills, T. T., & Hertwig, R. (2010). Information search in decisions from experience: Do our patterns of sampling foreshadow our decisions? Psychological Science, 21(12), 1787–1792.
Jessup, R. K., Bishara, A. J., & Busemeyer, J. R. (2008). Feedback produces divergence from prospect theory in descriptive choice. Psychological Science, 19(10), 1015–1022.
Kahneman, D., & Lovallo, D. (1993). Timid choices and bold forecasts: A cognitive perspective on risk taking. Management Science, 39(1), 17–31.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47(2), 263–291.
Konstantinidis, E., Ashby, N. J., & Gonzalez, C. (2015). Exploring Complexity in Decisions from Experience: Same Minds, Same Strategy. In CogSci.
Lejarraga, T., & Hertwig, R. (2016). How the threat of losses makes people explore more than the promise of gains. Psychonomic Bulletin & Review, 24(3), 708–720.
Lejarraga, T., Hertwig, R., & Gonzalez, C. (2012). How choice ecology influences search in decisions from experience. Cognition, 124(3), 334–342.
Lopes, L. L. (1987). Between hope and fear: The psychology of risk. Advances in Experimental Social Psychology, 20, 255-295.
Lopes, L. L., & Oden, G. C. (1999). The role of aspiration level in risky choice: A comparison of cumulative prospect theory and SP/A theory. Journal of Mathematical Psychology, 43, 286–313.
Paternoster, R., & Pogarsky, G. (2009). Rational choice, agency and thoughtfully reflective decision making: The short and long-term consequences of making good choices. Journal of Quantitative Criminology, 25(2), 103–127.
Peterson, C. R., & Beach, L. R. (1967). Man as an intuitive statistician. Psychological Bulletin, 68, 29–46.
Reyna, V. F., & Brainerd, C. J. (2008). Numeracy, ratio bias, and denominator neglect in judgments of risk and probability. Learning and Individual Differences, 18(1), 89–107.
Schwartz, G., (1978). Estimating the dimension of a model. The Annals of Statistics, 5, 461–464.
Stewart, N., Chater, N., & Brown, G. D. (2006). Decision by sampling. Cognitive Psychology, 53(1), 1–26.
Szrek, H., & Baron, J. (2007). The value of choice in insurance purchasing. Journal of Economic Psychology, 28(5), 529–544.
Tversky, A., & Kahneman, D. (1991). Loss aversion in riskless choice: A reference-dependent model. The Quarterly Journal of Economics, 106(4), 1039–1061.
Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5, 297–323.
Vlaev, I., Chater, N., Stewart, N., & Brown, G. D. A. (2011). Does the brain calculate value? Trends in Cognitive Sciences, 15(11), 546–554.
Vulkan, N. (2000). An economist’s perspective on probability matching. Journal of Economic Surveys, 14(1), 101–118.
Walasek, L., & Stewart, N. (2015). How to make loss aversion disappear and reverse: Tests of the decision by sampling origin of loss aversion. Journal of Experimental Psychology: General, 144(1), 7–11.
Wells, G. L., & Windschitl, P.D. (1999). Stimulus sampling and social psychological experimentation. Personality and Social Psychology Bulletin, 25(9), 1115–1125.
Wilson, T. D., Reinhard, D. A., Westgate, E. C., Gilbert, D. T., Ellerbeck, N., Hahn, C., ... & Shaked, A. (2014). Just think: The challenges of the disengaged mind. Science, 345(6192), 75–77.
Yechiam, E., & Ert, E. (2007). Evaluating the reliance on past choices in adaptive learning models. Journal of Mathematical Psychology, 51, 75–84.
Yechiam E., & Hochman, G. (2013). Losses as modulators of attention: Review and analysis of the unique effects of losses over gains. Psychological Bulletin, 139(2), 497–518.
Yechiam, E., Zahavi, G., & Arditi, E. (2015). Loss restlessness and gain calmness: durable effects of losses and gains on choice switching. Psychonomic Bulletin & Review, 22(4), 1096–1103.
Supplementary Table 1: Median model fit (BIC) and parameter values in the two study conditions for the problems involving mixed gains and losses in Study 2. Standard errors appear in parenthesis.
Condition Model fit (BIC) Diminishing sensitivity (γ) Loss aversion (λ) Recency (φ) Sensitivity (c) Decisions-from-Feedback 36.19 (23.0) 0.61 (.04) .88 (.34) .03 (.04) .58 (.38) Decision-to-Engage 34.01 (18.1) 0.45 (.04) .52 (.28) .02 (.03) .91 (.40)
Study 1
To explore what influenced participants to choose a higher value option when they did choose with consequence (did not choose the sure zero option), we performed a logistic regression predicting a choice of the higher value option by condition, choice set type (entered linearly and centered), and their interaction. We controlled for repeated measurement by clustering on the level of participant (Rogers, 1991). Only choice set type was significant with the rate of picking the higher value option being lower when losses were large (MGains = .68; MMixed +EV = .53; MMixed –EV = .44), Odds Ratio = .59, z = −6.68, p < .001. Other ps > .15.
Study 2.
To explore what influenced participants to choose a higher value option when they did choose with consequence (did not choose the sure zero option), we performed a logistic regression predicting a choice of the higher value option by condition, gamble type (entered linearly and centered), whether the riskier option was of higher value, as well as their respective interactions. We controlled for repeated measurement by clustering on the level of participant. We find that the likelihood of picking the higher EV option was lower as the overall value of the options decreased (i.e., going from the gain only to the mixed negative EV pair), Odds Ratio = .66, z = 5.19, p < .001, and increased when the riskier option was of higher value, Odds Ratio = 1.29, z = 2.12, p = .03. These effects are qualified by their interaction indicating that participants tended to prefer the riskier options when losses were larger (Riskier worse: MGains = .64; MMixed +EV = .54; MMixed –EV = .59; Riskier Better: MGains = .61; MMixed +EV = .46; MMixed –EV = .72), a preference which was rewarding when the riskier was better, but costly when it was not, Odds Ratio = 2.55, z = 7.23, p < .001. Lastly, we find that those in decisions-to-engage condition (M = .63; CI95% [.59, .66]) made more choices for the higher value options than those in the decisions-from-feedback (M = .57; CI95% [.55, .59]) condition, Odds Ratio = 1.26, z = 2.01, p = .04. None of the other interactions reached significance, ps > .07.
Ahn et al. (2008)’s learning model.
This model is based on prospect theory’s value function (Kahneman & Tversky, 1979) in that:
if x(t)>0: u(t) = x(t)γ
if x(t)<0: u(t) = −λ | x(t) |γ
where u(t) is the utility for outcome x in trial t; λ is the loss aversion parameter, which was constrained between 0 and 10; and γ is the diminishing sensitivity parameter, which was constrained between 0 and 1. The model further assumes that the participants learn from experience using a delta learning rule, as follows:
Ej(t) = Ej(t−1) + φ [ v(t) − Ej(t−1) ] where Ej is the expectancy (or propensity) of each option j, and φ is the learning rate parameter (validation of this learning assumption appears in Ahn et al., 2008).6 Choices are a stochastic function of the expectancies, as follows:
Pr[ Gj, (t+1) ] =
eφ Ej(t)
∑ k eφ Ek(t) where Pr[ Gj, (t) ] is the probability of selecting option G in trial t, and θ determines whether one is making more or less deterministic choices (i.e., whether the predicted choice proportion is determined according to the expectancies). As in Ahn et al. (2008) and Yechiam and Ert (2007), θ = 3c, and the range of parameter c was constrained between 0 and 10 (higher values of c imply greater determinism).
The fit of the model to the current two datasets was compared to a simple baseline model based on the optimized proportion of the choices of the different options: The baseline model prediction is the mean probability of selecting each alternative. A BIC test (Schwartz, 1978) was used to compare the baseline to the learning model, as follows: BIC = 2[Log Likelihood Model −Log Likelihood Baseline] − k · ln(t),
where k is the difference in the number of parameters between the learning model and baseline model (i.e., k = 2). Modeling took place as in Ahn et al. (2007). The results showed that model fits were adequate (mean BIC of 99.14, median of 22.13). Because the mean of the parameter estimates for λ is biased for loss aversion (e.g., mean of λ = 2 and λ = 0.5 is 1.25 despite the fact that the two estimates are equally loss averse and gain seeking), we used median parameters, as shown in Supplementary Table 1.
- *
- #
- $
Supported by the Leverhulme Trust (RPG-384), the I-CORE program (1821/12), and the Israel Science Foundation (199/12).
Copyright: © 2017. The authors license this article under the terms of the Creative Commons Attribution 3.0 License.
- 1
- 2
- 3
- 4
- 5
- 6