Judgment and Decision Making, Vol. 13, No. 4, July 2018, pp. 372-381

The present study investigated skilled and adaptive strategy selection in risky decision making. We proposed that people with high objective numeracy, a strong predictor of general decision making skill, would have a broad repertoire of choice strategies and adaptively select these strategies depending on the importance of the decision. Thus more objectively numerate people would maximize their effort (e.g., invest more time) in important, high-payoff decisions and switch to a simple, fast heuristic strategy in trivial decisions. Subjective numeracy would, by contrast, be more closely related to interest in problem solving for its own sake and would not yield such an effect of importance. Participants made twelve high-payoff choices and twelve low-payoff choices in binary two-outcome gambles framed as gains. We measured objective and subjective numeracy using standard measures. Results showed that people with high subjective numeracy generally maximized the expected value (EV) in all decisions. In contrast, participants with high objective numeracy maximized EV only when choice problems were meaningful (i.e., they could result in high payoffs). When choice problems were trivial (i.e., choosing the normatively better option would not result in a large payoff), more objectively numerate participants made choices consistent with faster, more frugal heuristic strategies.

Keywords: numeracy, strategy selection, risky choice, prospect theory, priority heuristic, skilled decision making, deliberation

1  Introduction

In real-life financial situations, people use various choice strategies and decision rules to deal with problems that involve processing of outcomes and probabilities. For instance, if we use the expected value (EV) maximization principle as a model of rational behavior under risk, the decision regarding whether or not to buy a lottery ticket for 3 EUR with a probability of winning a one-million main prize at 0.0000072%, should be preceded by optimization analyses that include calculations comparing EV of the bet (i.e., +0.072 EUR) with the certain loss of −3 EUR. However, comprehensive optimization is almost impossible in the majority of everyday decision problems, as they are usually very complex, dynamic and uncertain (people do not know every possible alternative, precise values of probabilities, etc.). Furthermore, apart from material and accountable consequences (e.g., money), people also attach value to other resources such as their effort and time spent on making a decision.

Many studies have reported that people with greater numerical abilities are more likely to make better choices in similar problems, that is, decisions more consistent with EV maximization (Cokely et al., 2018; Pachur & Galesic, 2013; Jasper, Bhattacharya, Levin, Jones & Bossard, 2013; Peters & Bjalkebring, 2015). Nonetheless, there is compelling evidence that superior decisions in more numerate people do not simply result from complex computations of EVs but rather they are driven by exhaustive considerations of multiple aspects of the problem (i.e., elaborate heuristic processing, Cokely & Kelley, 2009; Ghazal, Cokely & Garcia-Retamero, 2014; Jasper, Bhattacharya & Corser, 2017). The ability to understand and use statistical and probability information) is also related to superior decision making in both health and financial domains (Galesic & Garcia-Retamero, 2011; Garcia-Retamero, Andrade, Sharit & Ruiz, 2015; Ghazal et al., 2014, 2014; Reyna & Brnst-Renck, 2014) and is associated with greater personal wealth in general (Estrada-Mejia, de Vries & Zeelenberg, 2016). However, the question of how people with high numeracy arrive at better decisions seems to be complex.

Researchers argue that more (objectively) numerate individuals have better understanding of the gist of decisions (Reyna, Nelson, Han & Dieckmann, 2009), deliberatively employ metacognitive heuristics (Garcia-Retamero, Cokely & Hoffrage, 2015; Ghazal et al., 2014), draw precise affective meaning from numbers (Peters, 2012; Peters et al., 2006), and are more likely to conduct explicit number operations (Peters & Bjalkebring, 2015). Higher numeracy is also related to more exact mental number-line mapping (Schley & Peters, 2014) and more linear transformations of objective numbers (Millroth & Juslin, 2015), resulting in less pronounced distortions in processing outcomes and probabilities (Patalano, Saltiel, Machlin & Barth, 2015), although other results raise questions about this conclusion (Peters et al., 2006). Furthermore, people with higher objective numeracy seem to be less prone to affective influences during decision making (e.g., Petrova, van der Pligt & Garcia-Retamero, 2014; Traczyk & Fulawka, 2016; Traczyk et al., 2018).

A question posed here is whether those with higher objective numeracy are more inclined to adaptively change choice strategy depending on the task requirements. Do they allocate their time and effort in proportion to the importance of decisions? In particular, we investigated how the structure of the environment (operationalized as the difference in the magnitudes of expected payoffs) influences strategy selection under risk and what is the role of numeracy in this process. The present study thus investigated whether highly numerate individuals always engage more time and effort to compute EV, or rather adaptively select their choice strategy depending on the task and environment (Jasper et al., 2013).

Additionally, we examined the relative contribution of objective (i.e., inferred from the numerical task performance) and subjective (i.e., declared preference for numbers and number-related operations) numeracy in predicting choices. Although a measure of subjective numeracy has been shown to be a good proxy for objective numeracy (e.g., it predicts performance in numerical tasks; Fagerlin et al., 2007) and some researchers use objective and subjective numeracy scales interchangeably (Zikmund-Fisher, Smith, Ubel & Fagerlin, 2007), other studies have demonstrated that these tests measure different traits (Anderson, Obrecht, Chapman, Driscoll & Schulkin, 2011; Miron-Shatz, Hanoch, Doniger, Omer & Ozanne, 2014; Peters & Bjalkebring, 2015; Petrova et al., 2017). For instance, subjective numeracy predicts perceptions of health, whereas objective numeracy predicts actual health in patients (Garcia-Retamero et al. 2015). Taking this into account, in the present study we measured both subjective and objective numeracy to examine their relative contribution to choice.

1.1  Research problem and hypothesis

In this study, we ask whether people with high objective numeracy adapt their effort to the importance of the decision, or whether they simply make better decisions regardless of the importance of the decision. On the one hand, more numerate subjects are likely to make more normatively superior choices in financial problems as a result of greater deliberation during decision making (Ghazal et al., 2014). This effect can be presumably attributed to the elaborative heuristic search posited by Cokely and Kelley (2009) — a larger number of simple considerations as well as better understanding of formal operations with numbers. On the other hand, more numerate subjects could also strategically allocate deliberation time and use different choice strategies depending on the importance of a decision, quantified here by the EV ratio between gambles. That is, people high in numeracy would maximize their effort (e.g., invest more time and deliberation) when the decision really matters (i.e., when differences between expected payoffs are large), but when the decision is trivial (i.e., when differences between expected payoffs are small) they would switch to a simple and fast heuristic strategy.

Prior research suggests two potential outcomes. Firstly, in the case of trivial choice problems, more numerate individuals would behave similarly as in meaningful problems. That is, they will deliberate more on the problem, leading to more of their choices being consistent with EV (Ghazal et al., 2014; Jasper et al., 2017). Secondly, because of the adaptive sensitivity to changes in EV that is exhibited by more numerate people (Jasper et al., 2013), their ability to get the gist of numbers (Reyna et al., 2009) and to employ heuristic processing (Cokely & Kelley, 2009), they are expected to switch to a faster heuristic-based strategy as it provides comparable performance in case of decisions that seem trivial (i.e., low-payoff gambles with similar EVs).

---

Table 1: Twelve low-payoff (with EV ratios around 1) and twelve high-payoff (with EV ratios between 5 and 6) binary choice problems consisting of two-outcome gambles in the gain domain. The priority heuristic (PH) and cumulative prospect theory (CPT) predicted opposite choices. Each problem met criteria of nondominance.

Gamble A	Gamble B	EV Gamble A	EV Gamble B	EV ratio	Choice by PH	Choice by CPT
5.40, 0.29; 0, 0.71	9.70, 0.17; 0, 0.83	1.57	1.65	1.05	A	B
17.50, 0.17; 0, 0.83	3.00, 0.94; 0, 0.06	2.98	2.82	1.05	B	A
9.70, 0.17; 0, 0.83	5.40, 0.29; 0, 0.71	1.65	1.57	1.05	B	A
3.00, 0.29; 0, 0.71	5.40, 0.17; 0, 0.83	0.87	0.92	1.06	A	B
31.50, 0.17; 0, 0.83	5.40, 0.94; 0, 0.06	5.36	5.08	1.05	B	A
31.50, 0.29; 0, 0.71	56.70, 0.17; 0, 0.83	9.14	9.64	1.06	A	B
9.70, 0.17; 0, 0.83	3.00, 0.52; 0, 0.48	1.65	1.56	1.06	B	A
5.40, 0.17; 0, 0.83	3.00, 0.29; 0, 0.71	0.92	0.87	1.06	B	A
3.00, 0.52; 0, 0.48	9.70, 0.17; 0, 0.83	1.56	1.65	1.06	A	B
17.50, 0.52; 0, 0.48	56.70, 0.17; 0, 0.83	9.1	9.64	1.06	A	B
9.70, 0.52; 0, 0.48	31.50, 0.17; 0, 0.83	5.04	5.36	1.06	A	B
56.70, 0.17; 0, 0.83	17.50, 0.52; 0, 0.48	9.64	9.1	1.06	B	A
3.00, 0.17; 0, 0.83	56.70, 0.05; 0, 0.95	0.51	2.84	5.56	A	B
3.00, 0.94; 0, 0.06	31.50, 0.52; 0, 0.48	2.82	16.38	5.81	A	B
56.70, 0.05; 0, 0.95	3.00, 0.17; 0, 0.83	2.84	0.51	5.56	B	A
5.40, 0.94; 0, 0.06	56.70, 0.52; 0, 0.48	5.08	29.48	5.81	A	B
31.50, 0.52; 0, 0.48	3.00, 0.94; 0, 0.06	16.38	2.82	5.81	B	A
56.70, 0.52; 0, 0.48	5.40, 0.94; 0, 0.06	29.48	5.08	5.81	B	A
3.00, 0.94; 0, 0.06	56.70, 0.29; 0, 0.71	2.82	16.44	5.83	A	B
5.40, 0.52; 0, 0.48	56.70, 0.29; 0, 0.71	2.81	16.44	5.86	A	B
31.50, 0.29; 0, 0.71	3.00, 0.52; 0, 0.48	9.14	1.56	5.86	B	A
56.70, 0.29; 0, 0.71	5.40, 0.52; 0, 0.48	16.44	2.81	5.86	B	A
3.00, 0.29; 0, 0.71	56.70, 0.09; 0, 0.91	0.87	5.1	5.87	A	B
56.70, 0.09; 0, 0.91	3.00, 0.29; 0, 0.71	5.1	0.87	5.87	B	A
CPT and EV were always consistent in their choice predictions in these problems.

---

2  Method

2.1  Subjects

One hundred and thirty-nine volunteers from the general population (age range: 18–58 years; M_age = 29.21; SD = 8.57; 52% female) participated in an online study for a 30 PLN (Polish Zloty) compensation (equivalent to approximately 8 EUR).¹ Subjects were recruited via an advertisement published on a local webpage. Subjects received explicit information stating that the study examined cognitive abilities and were assured that payment was not related to their performance. Volunteers gave informed consent before the study.

---

Table 2: An example of cognitive operations and choice predictions according to cumulative prospect theory (CPT) and priority heuristic (PH).

	Gamble A: 29% probability to win 5.40 EUR or 71% probability to win nothing (0 EUR)	Gamble B: 17% probability to win 9.70 EUR or 83% probability to win nothing (0 EUR)
Cumulative prospect theory (CPT)
Step 1: compute the CPT value of a gamble	Using equation V =  ∑i = 1n w( pi )v( xi ), where w is the decision weight for probability pi, and v is a value of an outcome xi with standard CPT parameters (0.88 for the value function and 0.61 for the probability weighting function in gain domain), CPT values for Gamble A and B equal 1.38 and 1.78, respectively.
Decision: select the gamble with a higher CPT value	Select Gamble B because of the higher CPT value.
Priority heuristic (PH)
Step 1: is the difference in minimum gains larger than 10% of minimum gain?	No. Minimum gain in Gamble A (0 EUR) equals to the minimum gain in Gamble B (0 EUR)
Step 2: is the difference in the probability of the minimum gain larger than 10% in the probability scale?	Yes. 71% in Gamble A vs. 83% in Gamble B (the difference of 12% is larger than 10%). Thus, considering the last step posited by PH (i.e., the difference between maximum gains) is not necessary.
Decision: stop the process and select the gamble with a lower probability of minimum gain	Select Gamble A.
CPT and EV were always consistent in their choice predictions in these problems.

---

2.2  Design and materials

The study was designed to investigate the relationship between numeracy and choices under risk. We measured both subjective and objective numeracy as main predictors in this study as well as fluid intelligence and need for cognition. We also introduced a within-subjects manipulation of choice payoff (i.e., 12 low-payoff vs. 12 high-payoff binary two-outcome choice problems). The dependent variable was subjects’ choices in these problems. Response latencies in each problem were used to operationalize deliberation time and enhance our understanding of the cognitive processes underlying decision making.

Subjects completed the following measures:

2.2.1  The Berlin Numeracy Test

The Berlin Numeracy Test (BNT; Cokely, Galesic, Schulz, Ghazal & Garcia-Retamero, 2012) is a psychometric instrument that measures statistical numeracy, risk literacy and comprehension of the concept of probability. The BNT is widely used as an efficient research tool to measure objective numerical abilities (Cokely et al., 2012). In the current study, we used a computerized version of the BNT consisting of four items presented to subjects in a fixed order. Subjects were not forced to provide any response to complete the items.

2.2.2  The Subjective Numeracy Scale

Subjects completed the Subjective Numeracy Scale (SNS; Fagerlin et al., 2007), an 8-item self-assessment scale that measures subjective numeracy and includes two subscales referring to perceived numerical abilities (e.g., “How good are you at working with percentages?”) and preference for numerical and statistical information (e.g., “How often do you find numerical information to be useful?”). Subjects completed the SNS by answering each question using a 6-point scale.

2.2.3  The Need for Cognition Scale

Individual differences in epistemic motivation were assessed using the Need for Cognition Scale (NCS; Cacioppo & Petty, 1982). The Polish adaptation of the scale (Matusz, Traczyk & Gąsiorowska, 2011) includes 36 items and measures "the tendency for an individual to engage in and enjoy thinking" (Cacioppo & Petty, 1982, p. 116). The main goal of the NCS is to assess the individual’s level of joy and satisfaction emerging from the processes of thinking, resolving problems, learning new things, etc. Subjects used a 5-point scale to indicate the extent they agree with each statement (e.g., “Thinking is not my idea of fun”).

2.2.4  The Raven’s Advanced Progressive Matrices

To measure individual differences in fluid intelligence we used the Raven’s Advanced Progressive Matrices test (RAPM; Raven, 2000). The RAPM is a nonverbal test that is typically employed to assess basic cognitive functioning such as abstract reasoning. Problems included in this test are presented in the form of matrices (e.g., 3 x 3 elements) with one missing piece. The task is to figure out the rule underlying the uncovered elements and select the missing element that satisfies the appropriate rule. In the present study, we used a short form of the RAPM consisting of two training and six test matrices displayed with ascending difficulty.

2.2.5  Choice problems

We used twenty-four binary choice problems consisting of two-outcome gambles from a study by Pachur, Hertwig, Gigerenzer and Brandstätter (2013, Experiment 2). The outcomes of the choice problems were framed as gains. Choice problems differed in their EV ratios (Table 1), which we used to define high- and low-payoff problems. If the EVs of two gambles were similar (dividing their EVs led to outcomes around 1), then we classified them as low-payoff problems in comparison to high-payoff problems in which the EVs of the two gambles differed substantially (dividing their EVs led to outcomes between 5 and 6). In other words, low-payoff problems (with EVs ratios around 1) can be regarded as trivial, because playing them repeatedly would lead to relatively small differences in payoffs irrespective of the chosen gamble (i.e., it does not really matter which option you should select, because in the long-run a decision maker would get a similar payoff). In contrast, high-payoff problems (with EVs ratios between 5 and 6) are more meaningful, because their EVs differ and choosing the gamble with the higher EV will lead to much higher payoffs (i.e., it pays to choose the gamble with higher EV because differences in payoffs are large in the long run).

The problems were generated in such a way that two competing models of choice under risk — the priority heuristic (PH; Brandstätter, Gigerenzer & Hertwig, 2006) and cumulative prospect theory (CPT; Tversky & Kahneman, 1992) — always led to different predictions on choice. According to CPT, a decision-maker multiplicatively combines the subjectively transformed outcomes and their weighed probabilities to arrive at an overall value of a gamble. Next, a gamble with a higher value is chosen. In contrast, the PH posits that a decision maker relies on a series of sequential steps aimed at comparing gambles according to their minimum gains, the probabilities of these minimum gains, and the maximum gains (in fixed order). The sequence of comparative operations is stopped resulting in a choice when the difference between minimum (maximum) gains is larger than 10% of the minimum (maximum) gain, or if the difference in probabilities of minimum gains is larger than 10% of the probability scale (Table 2).

Let us illustrate the difference between CPT and PH in the following two gambles presented in the first row of Table 1, (Gamble A: 5.40, 0.29; 0, 0.71 and Gamble B: 9.70, 0.17; 0, 0.83). PH predicts that a decision maker will choose Gamble A because the difference in minimum gain probabilities is larger than 10% of the probability scale (i.e., 0.71 vs. 0.83). In contrast, CPT with standard parameters from Tversky and Kahneman (1992) predicts that a decision maker will choose Gamble B because of its greater CPT value (i.e., 1.38 vs. 1.78).

The choice of CPT and PH for assessing the gambles is not meant to imply that subjects conform to either theory. Rather it was intended to reflect the difference between simple heuristics and more compensatory approaches to decision making. In general, we expect CPT predictions to be the same as EV predictions.

2.3  Procedure

Subjects were instructed that they should complete the procedure individually during one session. Subjects also confirmed that they would focus on the task at hand and turn off other applications/music that could distract their attention. In reference to the BNT they were informed that they were not allowed to use calculators, but they could take notes on paper.

Tasks were administered with the InquisitWeb (2016) software and ran in pseudorandom order. Text was displayed in a black font on a light gray background. All subjects started by reading instructions and completing a demographic survey. They then completed a block of tasks including the BNT, RAPM, and choice problems (presented in random order), followed by another block which included the self-report measures of SNS and NCS (also presented in random order). Additionally, twelve low- and twelve high-payoff choice problems were mixed and presented to each subject in a different random order. At the end of the study, subjects declared whether we could include their data in the analyses. The entire procedure took approximately 40 minutes (although there were no time constraints). There was no immediate feedback regarding performance. However, after the study, subjects received information on their results in comparison to average scores calculated from the study sample.

---

Table 3: Descriptive statistics for measures used in the study. BNT – the Berlin Numeracy Test, NCS – the Need for Cognition Scale, RAPM – the Raven’s Advanced Progressive Matrices, SNS – the Subjective Numeracy Scale. CPT/EV-consistent choices in low- and high-payoff problems refer to the number of expected value choices in these problems.

	BNT	SNS	RAPM	NCS	CPT/EV-consistent choices in high-payoff problems	CPT/EV-consistent choices in low-payoff problems
Mean	1.75	34.87	3.71	131.9	8.8	4.41
SEM	0.11	0.67	0.13	1.66	0.27	0.27
Median	2	36	4	133	10	4
SD	1.27	7.88	1.48	19.38	3.17	3.15
Minimum	0	11	0	75	0	0
Maximum	4	48	6	171	12	11
N	139	139	136	136	138	138

---

---

Table 4: Pearson zero-order correlation coefficients for the relationships between measures used in the study. CPT/EV-consistent choices in low- and high-payoff problems refer to the number of expected value choices in these problems. BNT – the Berlin Numeracy Test, NCS – the Need for Cognition Scale, RAPM – the Raven’s Advanced Progressive Matrices, SNS – the Subjective Numeracy Scale. Deliberation time is log-transformed median choice latency.

	1	2	3	4	5	6	7	8
1. BNT	.	.503***	.529***	.214*	.344***	.281***	-.085	.301***
2. SNS		.	.372***	.428***	.315***	.196*	.200*	.323***
3. RAPM			.	.238**	.178*	.121	-.077	.241**
4. NCS				.	.237**	.163	.182*	.137
5. Deliberation time in low-payoff problems (log)					.	.807***	.144	.519***
6. Deliberation time in high-payoff problems (log)						.	-.106	.389***
7. CPT/EV choices in low-payoff problems							.	.340***
8. CPT/EV choices in high-payoff problems								.
* p < .05, ** p < .01, *** p < .001.

---

---

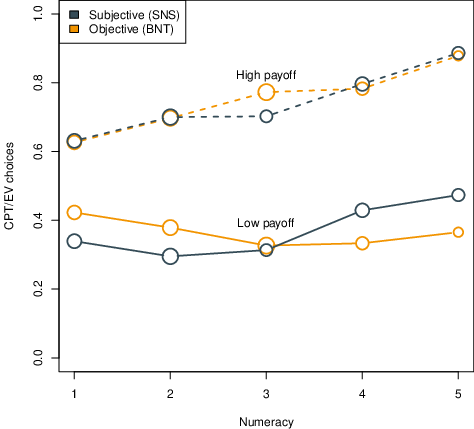
Figure 1: Proportion of choices consistent with expected value (CPT/EV) as a function of payoff (high/low, dashed lines are high) and numeracy (subjective in dark blue, objective in orange). Subjective numeracy (SNS) scores are displayed in quintiles (as equal as possible), so that the number of subjects in each point — represented by the area of each point — are roughly comparable to those for objective numeracy.

---

---

Table 5: Loadings on canonical variates (pairs of linear combinations of X and Y variables), CV1 and CV2.

	CV1	CV2
Four X’s
BNT	0.92	0.09
SNS	0.46	0.88
RAPM	0.76	0.08
NCS	0.03	0.61
Y’s with four X’s
CPT/EV choices	0.23	0.97
Payoff sensitivity	0.97	-0.23
Two X’s
BNT	0.92	-0.38
SNS	0.78	0.62
Y’s with two X’s
CPT/EV choices	0.61	0.79
Payoff sensitivity	0.79	-0.61

---

3  Results

Descriptive statistics for the measures used in the study and the correlations between them are presented in Table 3 and Table 4 respectively. Higher scores in the BNT, SNS, and RAPM as well as longer deliberation time were correlated with more choices consistent with CPT/EV in high-payoff problems. In low-payoff problems, only SNS and NCS, but not BNT or RAPM were positively correlated with CPT/EV-consistent choices. Of interest is the large difference between objective and subjective numeracy in predicting choices in low-payoff problems. In high-payoff problems, both objective and subjective numeracy strongly predicted CPT/EV choices, explaining almost twice as much variance as RAPM or NCS.

Figure 1 shows the different roles of subjective and objective numeracy by plotting a proportion of CPT/EV choices as a function of numeracy for high- and low-payoff conditions, for both subjective and objective numeracy. Note that the CPT/EV choice proportion increases with subjective numeracy for both payoff conditions, but the choice proportion increases with objective numeracy only for the high-payoff condition. Thus, higher objective numeracy (BNT) appears to lead to greater sensitivity to payoffs (greater difference between top and bottom lines in Figure 1).

To ask whether subjective and objective numeracy predict different aspects of performance, we calculated the mean proportion of CPT/EV-consistent choices for each subject and the difference between high- and low-payoff conditions in CPT/EV-consistent choices, to assess sensitivity to payoff.

Next, we asked whether these two components, CPT/EV choices and payoff sensitivity, were differentially affected by measures of individual differences used in the study. To do this, we used canonical correlation (fit by the R package yacca: Butts, 2012). The idea is to find a linear combination of the “X” variables (BNT, SNS, RAPM, NCS) that correlate with a linear combination of the “Y” variables (CPT/EV choices and payoff sensitivity), optimizing the weights for the two combinations so as to get the highest correlation. Then (in essence) repeat the process on the residuals, to see if a different pattern of weights can account for additional variance (here we can have only two of these canonical variates because we have only two Y variables). Table 5 shows the loadings (analogous to factor loadings) on the two canonical variates.

The top half of Table 5 shows the weights for all four X variables. The two objective X variables (BNT and RAPM) load mostly on CV1, which is most strongly related to Payoff-sensitivity, while the two subjective X variables (SNS and NCS) load on CV2, which is related to CPT/EV choices. The bottom half shows similar results using only the two numeracy measures as X variables. For both of these analyses (with four and two X variables), the second canonical variate was significant (p = .0024 and p = .0004, respectively, by Bartlett’s χ² test), indicating that the second canonical variate accounted for significant variance. Thus, the results cannot be explained in terms of a single underlying factor affecting all X and Y variables.

Finally, we investigated the relationships among payoff, choices and response times. Log response times were slower for the low-payoff condition, presumably because the decision was more difficult, and slower for the choice of the better option (CPT/EV-consistent choice), presumably because the choice was made after more thought. The latter effect was greater in the low-payoff condition.² Means (in msec, derived from the mean logs) were: 3631 for high payoff, CPT/EV choice; 3280 for high payoff, PH choice; 6542 for low payoff, CPT/EV choice; and 3364 for low payoff, PH choice. Mean log response times increased with both BNT (r=.32, p<.001) and SNS (r=.25, p=.003), but the two measures of numeracy did not differ significantly in any analysis, and, if anything, show effects opposite to those that might be expected given other results. Likewise, the two correlations did not differ for just the low-payoff condition (r=.33, p<.001 for BNT, r=.30, p=.001 for SNS; calculated with logs taken before averaging).

4  Discussion

In the present study, we demonstrated that more statistically numerate decision makers are able to strategically invest sufficient deliberation to make adaptive choices. When decisions really mattered and could result in high payoffs, people with high objective numeracy made normatively better choices predicted by CPT and EV. However, when decisions were trivial and did not matter because the payoffs of the available options were similar, those with high objective numeracy made choices predicted by a heuristic strategy (i.e., PH). These PH-consistent choices were also “better”, because they resulted in getting an equally good payoff without wasting additional time and effort that could be of more value than the negligible difference in payoff earned by selecting the CPT/EV-consistent option.

At first glance, it may seem counterintuitive that those with high objective numeracy did not always maximize EV. However, after deeper consideration, we can conclude that decision makers with high objective numeracy exhibited adaptive rationality as they tried to maximize payoffs when choice problems were meaningful and, at the same time, minimized effort when choice problems were trivial. What is a potential cognitive mechanism underlying these effects?

Accordingly, our findings are a straightforward demonstration that more numerate subjects adaptively selected their choice strategy on more important choices. Nevertheless, it is not clear whether they performed EV-like computations (i.e., multiplying outcomes and probabilities) or rather used sophisticated heuristic processing (i.e., transforming and comparing probabilities and outcomes, reframing the problem, and so forth). Although the choice problems we used in our study clearly distinguish between two choice models, the lack of more sophisticated process-tracing measures (e.g., eye tracking) does not allow us to conclude that subjects processed gambles accordingly. For instance, Cokely and Kelley (2009) demonstrated that choices consistent with EV rarely resulted from EV computations but they were driven by elaborative heuristic processing instead. Moreover, Pachur et al. (2013) also demonstrated that using simple heuristics (e.g., the equiprobable heuristic, the equal-weight heuristic, or the better-than-average heuristic, Brandstätter et al., 2006) can lead to the same choices as those predicted by CPT or EV models. Indeed, Pachur et al. (2013) documented that these trade-off heuristics reveled the same performance as CPT in problems with both similar and different EV ratios, but at the same time lead to the opposite predictions to PH. Therefore, different cognitive processes from those posited by CPT/EV can be responsible for CPT/EV-consistent choices. This research problem can be addressed in future studies using process-tracing measures like think-aloud protocols or Mouselab-type methods in order to reveal the underlying cognitive process.

4.1  The role of subjective and objective numeracy

Apart from a measure of objective numeracy, we also used scales measuring subjective numeracy as well as need for cognition and fluid intelligence. These measures were related to choices. In particular, SNS was associated with more CPT/EV choices in both low and high payoff problems. NCS correlated with choices in low-payoff problems, and RAPM was positively related to more choices that maximized EV in high-payoff problems. While objective numeracy was a marker of adaptive strategy selection, SNS was a persistent marker of CPT/EV choices. These results are in line with recent advances in numeracy theory and they show that objective and subjective numeracy (although often used interchangeably) map different numerical competencies, consequently eliciting different implications for decisions (Peters & Bjalkebring, 2015). Objective numeracy has been more strongly linked to number comparisons, operations, and calculations. Subjective numeracy, on the other hand, has been primarily linked to emotional reactions to numbers, preference for them as well as motivation and confidence in numeric tasks (Peters & Bjalkebring, 2015). This differentiation allows for qualitatively different predictions for subjective and objective numeracy that can help understand the role of these constructs in risky choices.

In light of our findings, it seems that objective numeracy is a marker of adaptive and meta-cognitive strategy selection related to numerical processing. Consistent with previous research (Ghazal et al., 2014; Petrova, Garcia-Retamero, Catena & van der Pligt, 2016), subjects with higher objective numeracy spent more time deliberating on problems, but they were also able to switch to a faster strategy when choice problems became more trivial (i.e., the differences in payoffs were small).

Higher subjective numeracy was related to EV maximization processes irrespectively of the problem payoff. Subjective numeracy may, in a sense, indicate additional utility from trying to solve a problem. If so, subjects with high subjective numeracy would be less sensitive to the lack of extrinsic reward. They may have simply found the task interesting enough so that they tried to find the best option even when it was clear that the two options did not differ much in their expected outcomes.

4.2  Conclusions

To summarize, we demonstrated that subjective and objective numeracy play different roles in choices under risk. While people with high subjective numeracy tried to maximize every decision irrespectively of its payoff, objectively numerate, skilled decision makers did not waste extra time thinking harder and longer about trivial problems. Importantly, these people were able to assess which problem is meaningful and adapt their choice strategy to maximize payoff.

References

*

Corresponding author Email: jtraczyk@swps.edu.pl

#

Wroclaw Faculty of Psychology, SWPS University of Social Sciences and Humanities, Wroclaw, Poland.

$

Andalusian School of Public Health (EASP), Granada, Spain. Medical Research Institute ibs.GRANADA, University Hospitals of Granada/University of Granada, Granada, Spain.

!

Mind, Brain, and Behavior Research Center, University of Granada, Spain; Harding Center for Risk Literacy, Max Planck Institute for Human Development, Berlin, Germany.

The research in this article was supported by the National Science Centre, Poland under grant 2015/17/D/HS6/00703 and the Foundation for Polish Science (FNP) under grant START (111.2016). The current research was also partially funded by the Ministerio de Economía y Competitividad (Spain) (PSI2014-51842-R). Dafina Petrova is supported by a Juan de la Cierva Fellowship (FJCI-2016-28279) from the Spanish Ministry of Economy, Industry, and Competitiveness.

Copyright: © 2018. The authors license this article under the terms of the Creative Commons Attribution 3.0 License.

1

One hundred and thirty-three subjects completed all tasks.

2

These effects were tested with a multi-level model with subjects and choices as crossed random effects. All effects, including the interaction, had 95% confidence intervals that excluded zero. The use of such a model was necessary because subjects differed in the number of choices of the better option in the two payoff conditions, so that choice and payoff were not orthogonal.

This document was translated from L^AT_EX by H^EV^EA.