Judgment and Decision Making, Vol. 13, No. 1, January 2018, pp. 73-78

Risk and reward are negatively correlated in a wide variety of environments, and in many cases this trade off approximates a fair bet. Pleskac and Hertwig (2014) recently proposed that people have internalized this relationship and use it as the basis for probability estimation and subsequent choice under conditions of uncertainty. Specifically, they showed that risky options with high-value outcomes are inferred to have lower probability than options offering a less valuable reward. We report two experiments that test a simple corollary of this idea. In both studies, participants estimated the magnitude of prizes offered by lotteries with known win-probabilities. The relationship between estimates and probabilities followed the power relationship predicted by the risk-reward heuristic, albeit with a tendency to overestimate outcome magnitude. In addition, people’s estimates predicted their willingness to take the gamble. Our results provide further evidence that people have internalized the ecological relationship between risk and reward in financial lotteries, and we suggest that this relationship exerts a wide-ranging influence on decision-making.

Keywords: risk, reward, judgment, choice.

1  Introduction

In a recent paper, Pleskac and Hertwig (2014) examined the relationship between probability and payoff in a range of natural environments, including roulette, horse-race betting, life insurance, dairy farming, and academic publishing. In all cases, there was a consistent negative association between probability and reward. For example, journals with a higher impact factor have a lower acceptance rate, and bull semen samples that are expected to produce greater increases in farm profitability are less likely to successfully fertilize the female.

Pleskac and Hertwig argued that this negative relationship arises because real-world lotteries tend towards a fair bet, such that a gamble which costs L to play and offers a prize of G will have win-probability P = L/G.¹ This can happen for a number of reasons. For example, in a market for gambles, sellers wish to offer low rewards with low probabilities, whereas buyers seek high rewards with high probabilities, driving the offered gambles towards an equilibrium in which the expected returns are equal to the stake. This is exemplified by roulette, where the payouts perfectly track the probabilities such that the expected net return (in the European version) is always a loss of 2.7% of the stake – a value very close to the fair-bet payout, with just a small shift in the house’s favour to keep the casino in business.

Pleskac and Hertwig (2014) further argued that people have extracted this environmental contingency and use it as the basis for judgment and choice. Specifically, they posited the risk-reward heuristic: when the probability of winning is unknown, infer that it is equal to L/G. They tested this in two studies. First, they offered lab participants the opportunity to play a lottery for real money; participants were told that the lottery cost $2 to play and that the prize was $2.50, $4, $10, or $20 (varied between-participants). Participants were confronted with an envelope and a bingo basket containing 100 balls and told that the envelope contained a number from 1–100 that determined their probability of winning. After finding out the number in the envelope, they would draw a ball and, if its number was equal to or less than the number in the envelope, they would win. Prior to opening the envelope, participants had to estimate the number of winning balls and decide whether to play. Study 2 was similar but conducted on-line using a hypothetical gamble and a wider range of prizes.

The results of both studies are replotted in Figure 1. In both cases, the estimated probability of winning clearly decreases as the size of the prize increases. The bottom panels show the results on a log-log plot and demonstrate that the judgments follow the functional form predicted by the risk-reward heuristic, but that there is a regressive effect: people overestimated small probabilities and underestimated large probabilities (e.g., Erev, Wallsten & Budescu, 1994). In other words, the data potentially support an error-prone application of the heuristic, which nonetheless strongly anchors participants’ probability estimates.

---

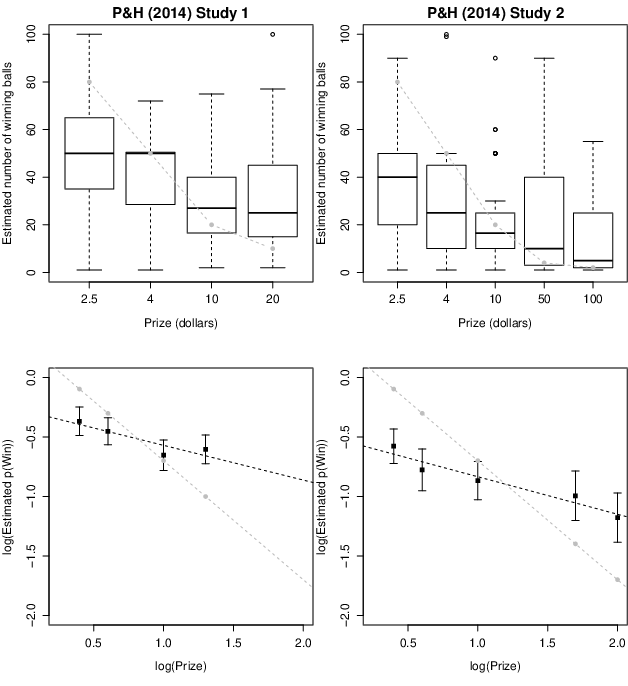
Figure 1: Results of Studies 1 and 2 from Pleskac & Hertwig (2014). The top panels show the distribution of estimated probability values for each prize condition. The grey dashed line indicates the predictions of the risk-reward heuristic. The bottom panels show the mean of the log-transformed estimates against the log-transformed prize values; the black dashed line shows the best-fitting linear function and the grey dashed line shows the predictions of the risk-reward heuristic. Error bars indicate 95% confidence intervals.

---

These estimates also predicted choice behaviour. At the aggregate level, participants in the high-outcome conditions (where the mean probability estimates were above what would be expected for a fair bet) were more willing to play the lottery than were those in the low-outcome conditions (where estimated probabilities were smaller than expected from a fair bet). At the individual level, regression analysis showed that both outcome value and estimated probability predicted the decision to play. However, the risk-reward heuristic is agnostic about the decision rule or process by which probability estimates shape choice. For example, the estimates may provide the basis for the calculation (and maximization) of expected value or expected utility (Savage, 1954), the computations of Prospect Theory (Kahneman & Tversky, 1979), or a process heuristic like elimination by aspects (Tversky, 1969).

We report two experiments that test a simple extension of the risk-reward heuristic: namely, that people use probabilities to infer rewards. Specifically, we test whether a person offered the chance to pay L to play a lottery that offers P chance of winning G will infer that G = L/P, and whether this inference predicts their decision about whether or not to play. This would be a logical consequence of the relation proposed by Pleskac and Hertwig (2014), but human estimates and choices routinely show asymmetries and task dependencies which mean this may not be observed in practice (e.g., Holyoak & Mah, 1982; Lichentstein & Slovic, 1971). The numerous differences in the ways that probabilities and monetary values are experienced, represented, and processed means that the principles by which people estimate rewards from probabilities need not be the same as those by which they estimate probabilities from rewards. Correspondingly, our experiments provide a straightforward but important test of the idea that people are sensitive to the ecological risk-reward trade-off. We note from the outset that gambles with explicit probabilities but uncertain outcomes are less common than those for which outcomes are explicit but probabilities are unknown (decisions under ambiguity). However, we believe that the impact of probability values on inferences about outcome magnitude nonetheless have implications for many risky choices, as we discuss below.

2  Method

---

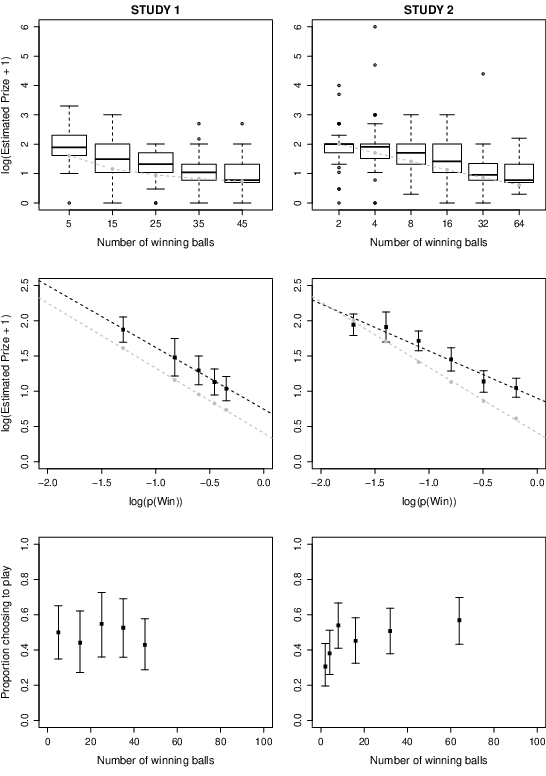
Figure 2: Results of Studies 1 and 2. The top panels show the distribution of estimated prize values for each probability condition. The grey dashed line indicates the predictions of the risk-reward heuristic. The middle panels show the mean of the log-transformed estimates against the log-transformed probabilities; the black dashed line shows the best-fitting linear function and the grey dashed line shows the predictions of the risk-reward heuristic. The bottom panels show the proportion of participants in each condition who chose to play the gamble. Error bars indicate 95% confidence intervals.

---

Both experiments were modelled closely on Pleskac and Hertwig’s (2014) Study 2. Participants were told about a hypothetical lottery which costs $2 to play and which offers a prize with a probability that was varied between participants. Participants had to estimate the prize and then state whether they would choose to play. Our Study 2 was a replication and extension of Study 1, using a larger sample, a wider range of probabilities, more stringent checks for attentiveness, and a clearer statement of the choice that participants were asked to consider. Given the similarity between the two experiments, we report them together.

2.1  Participants

Like Pleskac and Hertwig’s (2014) Study 2, both experiments were conducted on-line using participants from Amazon’s Mechanical Turk. Eligible participants were those aged 18 or over who completed the task and whose ip address had not previously occurred earlier in the data file, and who indicated that they had not previously attempted the task (see e.g., Matthews & Dylman, 2014). Study 1 recruited 205 eligible participants, of whom 7 failed an attention check leaving a final sample of 198 (114 male) aged 20–61 (M=35.9, SD=10.7). Study 2 recruited 411 eligible participants of whom 40 failed one or both attention checks, leaving a final sample of 371 (226 male) aged 18–79 (M=34.0, SD=10.3).

2.2  Design and Procedure

In Study 1, participants provided informed consent and were told that they would be asked to consider a simple financial decision which, although hypothetical, they should consider carefully and answer as honestly and accurately as they can. They then read the following instructions, which are closely modelled on those used by Pleskac and Hertwig (2014):

Imagine you have been asked to play the following lottery. The lottery offers the opportunity to win a monetary prize but it costs you $2 to play. If you choose to play you would pay the $2 and, without looking, draw a ball from a basket. In the basket there are 100 balls. The balls are either black or red. If the ball is red you will win the prize; otherwise, if the ball is black you will receive nothing. Thus, the number of red balls in the basket determines the probability that you will win. Given that the number of red balls in the basket is [5, 15, 25, 35, 45], how much do you estimate the prize to be?"

After entering their judgment, participants progressed to a page which asked: “Given the opportunity, would you pay $2 to play the gamble for your estimated prize money?” and selected "yes" or "no".

There followed an attention check question, which asked the colour of the winning balls (Red, Blue, Green, Yellow, or "I don’t know"), followed by a question probing past-participation and demographic information.

Study 2 was very similar, except for 3 changes. First, a wider range of probabilities was used (2, 4, 8, 16, 32, and 64 winning balls). Second, the choice task was modified so as to remind participants of the probability of winning and of their estimate of the prize, as follows: “Suppose that your estimate of the prize money is correct. That is, there are 100 balls in the basket, of which [2, 4, 8, 16, 32, 64] are red. If you draw a red ball, you win $[participant’s estimate of prize]. Would you pay $2 to play this lottery?” Third, an additional attention-check was added, which asked how many winning balls are in the basket.

3  Results

3.1  Prize estimates

As one would expect for judgments of financial value, participants’ estimates were positively skewed; we therefore applied a logarithmic transformation (log₁₀(x + 1)), after which the data were approximately normal within each condition. The top panels of Figure 2 show the data for each condition. As can be seen in the figure, participants’ estimates of the prize decreased as the probability of winning increased. The sensitivity of prize estimates to probability was confirmed by a one-way ANOVA for both Experiment 1, F(4, 193) = 13.00,  p <.001,  η² = .212, and for Experiment 2, F(5, 365) = 22.22,  p < .001,  η² = .233. The pattern is clearer in the middle panels of Figure 2, which show the data on a log-log plot along with the best fitting line and the linear function predicted by the risk-reward heuristic. The data match the functional form of the risk-reward heuristic, although in both studies participants consistently overestimated the size of the reward relative to that expected from a fair bet; in Study 2, this tendency becomes more pronounced as the probability of winning increases, echoing the regressive effect reported by Pleskac and Hertwig (2014) (see also Matthews & Stewart, 2009). The complementary regressive effects found here (where participants estimated rewards from stated probabilities) and in Pleskac and Hertwig (where people estimated probabilities from stated rewards) is reminiscent of work by Erev et al (1994), who showed that noise in the construction of subjective confidence leads to two complementary regressive tendencies: apparent overconfidence when one plots percentage-correct against subjective confidence categories but apparent underconfidence when one plots mean subjective probabilities against objective probability categories.²

3.2  Choice task

The proportion of participants who chose to play the lottery is plotted in the bottom panels of Figure 2. To test the effects of probability and estimated prize money on the willingness to play, we fit a series of logistic regression models and used likelihood ratio tests to compare them. The Null model included only an intercept; the Probability model included an intercept and the number of winning balls, coded as a categorical predictor (rather than positing a particular functional form for the effect); the Prize model included the intercept and the log-transformed estimates of the prize money; and the Full model included an intercept and both predictors.

For Study 1, the willingness to gamble was positively related to participants’ estimates of the prize money: the Prize model was superior to the Null model, χ²(1) = 14.98, p<.001, B_prize = 0.843, CI_95% = [0.407, 1.310], and the Full model was better than the Probability model, χ²(1) = 18.23, p <.001, B_prize = 1.076, CI_95% = [0.565, 1.633]. In contrast, the Probability model was no improvement over the Null model, χ²(4) = 1.69, p = .793, and the Full model was no better than the Prize model, χ²(4) = 4.93, p = .294. In short, choices were predicted by participants’ estimates of the prize money but not by the probability of winning. As an additional exploration, we re-ran the analyses using the logarithm of the number of winning balls, log₁₀(n), as a continuous predictor, in place of the categorical condition predictor. The pattern of the results was unchanged: there was a strong effect of the estimated prize, B_prize = 1.071, CI_95% = [0.562, 1.626], p <.001, but little effect of the number of winning balls, B_nwin = 0.846,CI_95% = [−0.074, 1.804], p = .076.

For Study 2, the willingness to gamble was again positively related to the estimated prize money: the Prize model was superior to the Null model χ²(1) = 15.59, p <.001, B_prize = 0.603, CI_95% = [0.296, 0.928], and the Full model was better than the Probability model χ²(1) = 41.11,  p <.001, B_prize = 1.295, CI_95% = [0.859, 1.769]. However, unlike Study 1 there was also an effect of the win-probability: the Probability model was superior to the Null model, χ²(5) = 12.65, p <.027, and the Full model was better than the Prize model, χ²(5) = 38.17, p <.001. Again, using the log-transformed number of winning balls as a continuous predictor revealed the same pattern: B_prize = 1.299, CI_95% = [0.868, 1.768], p <.001, B_nwin = 1.568, CI_95% = [1.030, 2.138], p < .001.

3.3  Potentially spurious responses

A total of 15 participants (10 in Study 1, 5 in Study 2) estimated the prize as $0; a further 6 (1 in Study 1, 5 in Study 2) gave very large estimates (> $1000). Our preference is to take all responses at face value (it is not unusual for lotteries to offer very large prizes, or for them to be rigged such that the player cannot win anything), but such responses might arguably be typos or indicate failure to understand the task. Re-running all analyses without these responses made very little difference to the plots or to the inferential tests, except that for Study 2 the improvement of the Probability model over the Null model was no longer significant, χ²(5) = 10.44,  p = .064; however, the Full model was still superior to the Prize model, χ²(5) = 41.90,  p <.001, indicating that the probability of winning predicted the decision to play, over and above the person’s estimate of the potential reward. When the log-transformed number of winning balls was used as a continuous predictor, the conclusions were the same: for Study 1, B_prize = 1.031, CI_95% = [0.454, 1.647], p <.001, B_nwin = 0.755, CI_95% = [−0.190, 1.736], p = .123; for Study 2, B_prize = 1.696, CI_95% = [1.194, 2.237], p <.001, B_nwin = 1.761, CI_95% = [1.185, 2.373], p < .001.

4  Discussion

Just as people judge that higher rewards will be associated with lower probability of success (Pleskac & Hertwig, 2014), so they judge that higher probabilities will be associated with lower rewards (our Studies 1 and 2). In both cases, the relationship is approximately linear on a log-log plot, consistent with the functional form predicted by the risk-reward heuristic. To this extent, both sets of studies support that heuristic as an account of inference about the components of a risky prospect.

However, like Pleskac and Hertwig’s data, our results are inconsistent with a strong (error-free) application of the heuristic. In particular, our participants tended to overestimate the probability of winning relative to what would be expected from a fair bet. This is surprising when one considers that many financial lotteries are actually designed to favour the house (for example, had our participants internalized the risk-reward structure of casino bets, state lotteries, or bookmakers’ odds, they would have estimated prizes that were smaller than the risk-reward heuristic would predict). This could be taken as an example of an optimism bias (see, e.g., Krizan & Windschitl, 2007). However, like the regressive effect in Pleskac & Hertwig’s data (and apparent in our Study 2), the optimism shown by our participants may be due to noisy responding: estimates of monetary reward are bounded at zero, so positive errors will tend to be larger than negative ones. More generally, the fact that probabilities are doubly-bounded (at zero and one) whereas rewards are only lower-bounded may mean that the precise consequences of applying the risk-reward heuristic will be different for the two types of estimation task. In any case, our data support the idea that the risk-reward heuristic anchors, but does not completely determine, people’s estimates of probabilities and outcomes.

These estimates influenced choice: in both studies, participants who expected larger rewards were more likely to take the gamble. Notably, our studies, like those of Pleskac and Hertwig (2014), always required participants to make their estimates prior to making their choices (because the primary interest is in whether people apply the risk-reward heuristic when estimating probabilities and outcomes); it remains to be seen whether the same relationship holds when choices precede estimation.

Researchers often focus on decisions under ambiguity, where the probability of an outcome is not precisely known. Indeed, Pleskac and Hertwig (2014) suggested that the risk-reward heuristic may contribute to the widespread aversion to ambiguous options, and provided some evidence for this possibility. Prima facie, there are fewer situations in which precise probabilities are given for uncertain outcomes. Although there are such scenarios (e.g., when a doctor states that a treatment has a 50% chance of being successful without defining "success"), a more important observation is that most real decisions take place in complex, information-rich environments that add considerable noise to the representation of outcomes and probabilities. It is easy to mis-read, mis-hear, or imperfectly process one or more components of an option, and in many situations the elements of competing options are not simultaneously presented but require retrieval from memory. In such situations, people use prior knowledge and schemas to inform their perceptions and memories (e.g., Ghosh & Gilboa, 2014; Vincent, 2015), such that inferences about outcomes from probabilities, just like inferences about probabilities from outcomes, will shape the mental representation of the decision.

Thus, even when precise information about probabilities and outcomes is ostensibly available, in practice people are likely to rely on prior beliefs and schemas to infer elements of the decision problem, and these inferences will shape the choice that is made. In other words, we contend that the risk-reward heuristic is likely to be an important, computationally-rational strategy in a wide variety of settings.

References

*

Department of Psychology, University of Cambridge, Cambridge UK. Email: wjm22@cam.ac.uk

Copyright: © 2018. The authors license this article under the terms of the Creative Commons Attribution 3.0 License.

1

Pleskac and Hertwig use a slightly different notation in which G refers to the winnings over and above the return of the stake, in which case P = L/(L+G); for the lottery-type scenarios considered in the current paper, we prefer to use L to denote the cost of a ticket and G as the prize.

2

We thank a Reviewer for pointing out this connection

This document was translated from L^AT_EX by H^EV^EA.