Judgment and Decision Making, Vol. 12, No. 6, November 2017, pp. 537-552
Further evidence for the memory state heuristic: Recognition latency predictions for binary inferencesMarta Castela*
Edgar Erdfelder#
|
According to the recognition heuristic (RH), for decision domains
where recognition is a valid predictor of a choice criterion,
recognition alone is used to make inferences whenever one object is
recognized and the other is not, irrespective of further
knowledge. Erdfelder, Küpper-Tetzel, and Mattern (2011) questioned
whether the recognition judgment itself affects decisions or rather
the memory strength underlying it. Specifically, they proposed to
extend the RH to the memory state heuristic (MSH), which assumes a
third memory state of uncertainty in addition to recognition
certainty and rejection certainty. While the MSH already gathered
significant support, one of its basic and more counterintuitive
predictions has not been tested so far: In guessing pairs (none of
the objects recognized), the object more slowly judged as
unrecognized should be preferred, since it is more likely to be in a
higher memory state. In this paper, we test this prediction along
with other recognition latency predictions of the MSH, thereby
adding to the body of research supporting the MSH.
Keywords: recognition heuristic, memory-state heuristic, threshold models, multinomial processing tree models
1 Introduction
The recognition heuristic (RH) is a fast and frugal decision
strategy proposing that, for binary decisions, if one object is
recognized and the other is not, one should infer that the
recognized object scores higher on the criterion under consideration
(Goldstein and Gigerenzer, 2002). This simple decision rule has gained a lot of
attention, and a large body of research was dedicated to it
(see Gigerenzer and Goldstein, 2011; Pachur et al., 2011, for reviews). However, one key
concept of the RH has often been neglected:
recognition. While literally at the core of the heuristic,
only a modest amount of research has focused on understanding the
role of recognition in use of the RH (e.g., Erdfelder, Küpper-Tetzel and Mattern, 2011; Pachur and Hertwig, 2006; Pleskac, 2007; Castela et al., 2014; Castela and Erdfelder, 2017). Notably, Erdfelder, Küpper-Tetzel and Mattern
proposed a framework that extends the RH by accommodating the role
of recognition memory, the memory state heuristic (MSH). Their
framework was later also supported by Castela et al. (2014) and
Castela and Erdfelder (2017) using formalizations of the MSH in the
framework of multinomial processing tree models (Batchelder and Riefer, 1999; Erdfelder et al., 2009). In this paper, we primarily aim to test a
crucial and counterintuitive prediction that has not been directly
addressed before and conflicts with the popular notion that
processing fluency – or cognitive fluency in general – boosts
preference for a choice option (Schooler and Hertwig, 2005; Zajonc, 1968). In addition, we provide support for the MSH through
conceptual replications of predictions previously tested by
different researchers (Erdfelder, Küpper-Tetzel and Mattern, 2011; Hertwig et al., 2008; Hilbig, Erdfelder and Pohl, 2011; Schooler and Hertwig, 2005; Pohl et al., 2016). In this way, we aim at closing a gap in
previous research on the MSH and provide converging evidence on the
importance of memory strength (rather than recognition judgments) in
recognition-based decision making.
This paper will be organized as follows: First, we will
introduce the RH and discuss how recognition memory has so far been
understood in its context. Second, we will introduce the MSH and
describe the evidence relevant to it. Third, we will report our two
new studies that complement the body of work on the MSH, each
consisting of a re-analysis of previously published data and a new
experiment.
1.1 The Recognition Heuristic
To better understand how recognition memory has been (or can be)
integrated in the RH, it is first essential to describe more precisely
how the heuristic has been proposed. To simplify that process, we will
refer to the most prominent paradigm associated with the RH as an
illustrative example. This is the city size paradigm, which involves a
paired comparison task and a recognition task. In the paired
comparison task, participants must infer which of two cities has a
larger population. In the recognition task, participants are asked to
indicate for each city involved whether they have heard of it (yes)
before the study or not (no). With the data from this recognition
task, all pairs of cities in the comparison task can be categorized
into three types: knowledge cases (both objects are recognized),
recognition cases (one object is recognized and the other is not), and
guessing cases (none of the objects is recognized). The RH applies
only to recognition cases, for the obvious reason that it cannot
discriminate between objects in the other two types of pairs.
Importantly, Gigerenzer and Goldstein (2011) specified additional preconditions for
use of the RH. First, there should be a strong correlation between
recognition and the decision criterion. In our example, recognition
should be strongly correlated to the size of a city (which, indeed, it
is). Additionally, further cues should not be readily available. This
means that, for example, when comparing the sizes of Berlin and
Mannheim, the information that Berlin is the capital of Germany, or
that it has an international airport, should not be presented to the
participant simultaneously (whereas, of course, it could be retrieved
from memory). Finally, they asserted that the RH applies only to
natural recognition, that is, artificially inducing recognition in the
laboratory (by, for example, presenting objects to the participants
several times) should not necessarily lead to use of the RH.
1.2 Recognition memory in the context of the RH
In the previous section we outlined the basic concepts surrounding the
recognition heuristic, but it is still unclear how the memory
processes underlying recognition influence use of the heuristic. In
its original definition, the RH was not related to recognition memory,
but only to recognition judgments. Goldstein and Gigerenzer (2002) assumed that the
RH works on the output of the recognition process, and that the
process itself can be disregarded. In other words, they assumed the RH
operates on yes or no recognition judgments, and whatever
underlies that judgment can be ignored for the purpose of
investigating the heuristic. This assumption implies that the
frequency with which an object has been encountered does not affect
use of the RH, and only the final all-or-none process of remembering
any encounter or not will matter. It follows that the RH will treat
objects with different memory strengths equally, as long as they are
both recognized or unrecognized. Erdfelder, Küpper-Tetzel and Mattern (2011) challenged
the notion that memory strength should not influence use of the
RH. Specifically, they argued that “Showing that the RH is an
ecologically rational and well-adapted choice strategy obviously
requires a formal theoretical link between (1) the memory strengths of
choice option names — a latent variable which is affected by
environmental frequency and previous processing — and (2) binary
recognition judgments for choice option names — an empirical
variable which is assumed to affect decision behavior.”
Following from this understanding of a necessary link between memory
strengths and recognition judgments, Erdfelder, Küpper-Tetzel and Mattern (2011) proposed
to integrate a model of recognition memory with the RH theory. To do
so, they relied on one of the most well-supported models of
recognition memory available — the two-high-threshold (2HT) model
(Kellen, Klauer and Bröder, 2013; Snodgrass and Corwin, 1988). Importantly, besides being
one of the most successful models of recognition memory, the 2HT model
has the added advantage of being easily combinable with the RH
(Erdfelder, Küpper-Tetzel and Mattern, 2011).
The 2HT model belongs to the class of multinomial processing tree
models (Batchelder and Riefer, 1999; Erdfelder et al., 2009). Like other multinomial
processing tree models, the 2HT model is based on the assumption that
observed categorical responses emerge from a defined set of discrete
states and that the probability of such states being entered depends
on the probability of certain cognitive processes occurring or
not. The basic premise of the 2HT model is that there are three
possible memory states underlying recognition judgments —
recognition certainty, uncertainty, and rejection certainty. The
probability of those states being entered depends on the probability
of two thresholds being exceeded (Figure
1). Specifically, for objects experienced before, if the
memory strength exceeds the first threshold with probability r, the
object will be in the recognition certainty state and a yes
recognition judgment will be given. If, with complementary probability
1−r, the memory strength lies below this threshold, the object will
be in the uncertainty state, and the recognition judgment will depend
on a second process of guessing, resulting in a yes judgment with
probability g and a no judgment with probability 1−g. For
objects not experienced before, if the memory strength lies below the
second threshold with probability d, the object will be in the
rejection certainty state and a no recognition judgment will be
given. With complementary probability 1−d, the memory strength lies
above this second threshold and the object will be in the uncertainty
state, just like unrecognized objects experienced before. Again, the
recognition judgment will depend on guessing yes or no with
probabilities g and 1−g, respectively.1
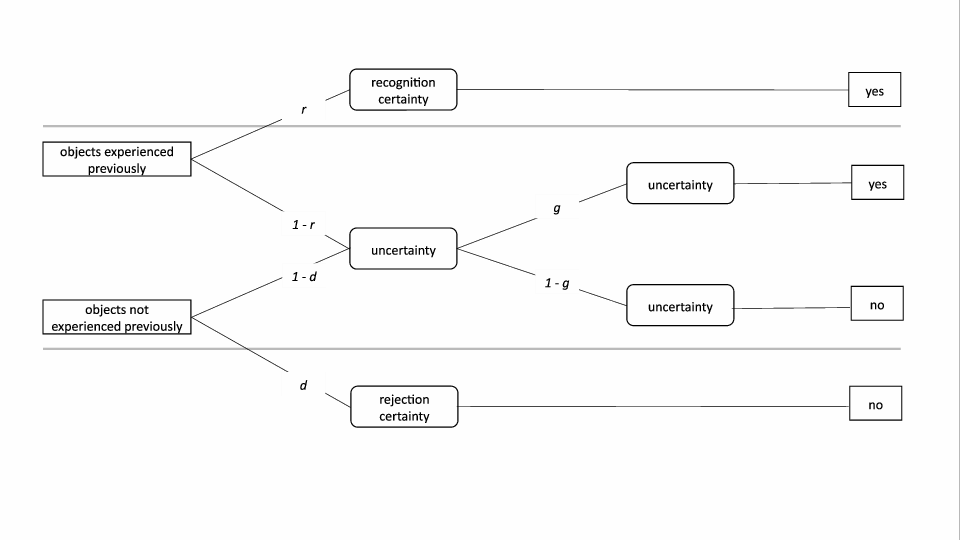
| Figure 1: Graphical representation of the two-high-threshold model. Parameter r denotes the probability of old objects exceeding the recognition threshold. Parameter d denotes the probability of new objects falling bellow the rejection threshold. Parameter g denotes the conditional probability of guessing yes in the uncertainty state. |
To combine this model with the RH theory, Erdfelder, Küpper-Tetzel and Mattern (2011)
suggested a new framework — the memory state heuristic (MSH). The
MSH is a straightforward extension of the RH, which mainly replaces
recognition judgments by memory strengths. That is, it assumes that
memory strengths, and not recognition judgments per se, affect
decision behavior. This simple extension enriches both the predictions
that can be drawn and the explanatory scope of the heuristic. Whereas
the RH has predictions for recognition pairs (i.e., recognition cases)
only, the MSH has predictions for any pair that involves objects in
different memory states. These predictions can be summarized by two
simple premises: (1) if objects are in different memory states, there
should be a preference for the object in a higher state; (2) the
larger the discrepancy between the memory states of objects in a pair,
the higher should be the probability of choosing the object in a
higher state. By implication, the probability of choosing the object
in the higher state should be larger for pairs of one object in the
recognition certainty state and the other in the rejection certainty
state than for pairs where one of the objects is in the uncertainty
state. Based on these two principles, Erdfelder, Küpper-Tetzel and Mattern
could both explain previous results that challenged the RH and also
draw and test new predictions. To do so, they relied on the fact that
multinomial processing tree models like the 2HT model can be
interpreted as probabilistic serial processing models
(Batchelder and Riefer, 1999; Heck and Erdfelder, 2016). By implication, the number of
cognitive processing stages in a given branch of the model will
influence its total processing time. Specifically, in the case of the
2HT model, whenever an object reaches the memory state of uncertainty
and a second cognitive process — guessing — is required, the
response time distribution should be stochastically larger than when
an object reaches one of the two certainty memory states
(Heck and Erdfelder, 2016). Following from this interpretation of the 2HT
model, a clear prediction can be made: “The larger the recognition
judgment latencies, the more likely it is that the judgment originates
from guessing and the less likely it is that it originates from memory
certainty” (Erdfelder, Küpper-Tetzel and Mattern, 2011, p. 13).
The MSH improves on the RH by offering a straightforward explanation
to results that have challenged the latter. Specifically, the
observation that factors beyond recognition (e.g., speed of
recognition, availability of further knowledge) seem to affect the
preference for the recognized objects has suggested that there is no
non-compensatory use of recognition. However, Erdfelder, Küpper-Tetzel and Mattern (2011)
argued that those findings can be easily accommodated by the MSH. For
example, the observation that recognized objects that are recognized
faster are preferred over those recognized more slowly
(Hertwig et al., 2008; Marewski et al., 2010; Newell and Fernandez, 2006) has been
interpreted as suggesting that retrieval fluency is also driving the
inference. However, the MSH would predict this preference because
objects recognized faster are more likely to be in the recognition
certainty state than the ones recognized more slowly
(Erdfelder, Küpper-Tetzel and Mattern, 2011). Another example discussed by
Erdfelder, Küpper-Tetzel and Mattern (2011) concerns the finding that RH accordance rates
(proportion of times the recognized object is chosen in recognition
pairs) are larger when RH-consistent inferences are correct than when
they are incorrect (Hilbig and Pohl, 2008). While this observation may
suggest that further knowledge is involved in the inferential process,
a different interpretation follows from the MSH: Recognition pairs
originating from recognition and rejection certainty states should
lead to correct inferences more often than the ones associated with at
least one object in the uncertainty state, simply because recognition
validity (i.e., the correlation between recognition and the criterion)
is higher for these pairs.
The fact that the MSH offers an explanation for these controversial
results suggests that it can be an important extension of the
RH. Furthermore, the MSH has found a considerable amount of other
support. First, Erdfelder, Küpper-Tetzel and Mattern (2011) tested seven predictions of
the MSH, focused on RH accordance rates and decision latencies, both
as a function of recognition and rejection latencies. The first three
predictions, which state that RH accordance rates should increase with
decreasing recognition and rejection latencies, and that their effect
is additive, were supported in their study. Additionally, they tested
whether the decision latency in recognition pairs increases with both
the recognition latency of the recognized object and the rejection
latency of the unrecognized object, and that their effect is
additive. These further three predictions were also supported by their
data. Finally, they found support for their seventh prediction, which
stated that response bias manipulations (aimed at selectively
affecting the guessing probability) in the recognition test should
affect recognition judgments but not performance in the comparison
task. Since the RH theory assumes that recognition judgments per se
influence decisions, it would predict that a bias manipulation will
also affect inferences. The MSH, in turn, predicts the observed
result, since memory-states rather than recognition judgments should
influence decisions, that is, since biasing the guessing probability
does not alter the memory-states distribution, inferences should be
left unaffected.
Additionally, Castela et al. (2014) also found support for the
MSH. They tested the predictions of (a) the RH, (b) knowledge
integration accounts, and (c) the MSH regarding the proportion of
RH-use for cases where the recognized object is said to be only merely
recognized versus recognized along with further knowledge. While the
RH predicts there should be no difference, since recognition alone
should drive inferences in recognition pairs, knowledge integration
accounts predict that RH-use should be lower when there is knowledge,
since when there is further information on which we could base the
inferences then we should not rely only on recognition. Notably, the
MSH predicts the opposite pattern, since recognized objects for which
there is further knowledge are more likely to have originated from
recognition certainty than objects that are merely
recognized. Reliance on the memory state should therefore be higher
for the former. Through a reanalysis of 16 published data sets,
Castela and collaborators showed that RH use is in fact more frequent
when there is knowledge about the recognized object, a result that is
predicted by the MSH and at odds with the other two accounts.
Finally, Castela and Erdfelder (2017) comprehensively tested the MSH by
developing a formal model that incorporates its predictions for all
possible memory-state combinations. We showed that restricting this
model to hold the core prediction of the MSH, namely, that MSH-use is
higher when the distance between memory-states is highest, leads to no
significant increase in model misfit, thereby suggesting that such a
model is consistent with the data. This is, to our knowledge, the most
thorough and elaborated test of the MSH so far. Given all these
results, it appears that the MSH is a well-supported framework which
should be seriously considered as an important extension of the RH.
It is at this point clear that there is considerable evidence
supporting the MSH. However, when we want to advocate the MSH, we must
ensure that the support for it does not depend on the decision domain
employed, on testing a limited number of predictions, on using
specific methods of evaluation, or on referring to a limited set of
proxy measures for underlying memory states. Probably most
importantly, especially the bold and surprising predictions of the MSH
need to be tested exhaustively, as these predictions most likely allow
us to discriminate between the MSH theory and other theories of
inferential decision making. Therefore, the primary aim of the present
work is to address a previously untested counterintuitive prediction
of the MSH regarding choices between pairs of objects, both of which
are unknown to the decision maker. Moreover, we also aim at
conceptually replicating and extending results previously tested in
different decision contexts or with different measures of MSH use. In
this way, we hope to close existing gaps and provide converging
evidence that solidifies the body of research on the MSH.
The focus of Erdfelder, Küpper-Tetzel and Mattern (2011) has been on testing predictions
for recognition pairs, but as explained before, the MSH also makes
predictions for guessing and knowledge pairs, as long as the objects
under comparison are in different memory states. This will be the
focus of our first study. As for recognition pairs, the predictions
follow from the basic premise of the MSH: If objects are in different
memory states, there should be a preference for the one in a higher
state. Therefore, in this study we will test two predictions:
-
In knowledge pairs there should be a preference for the object
recognized faster (as this one is more likely in the memory
certainty state)
- In guessing pairs, there should be a preference for the object
recognized more slowly (since this one is more likely in the
uncertainty state, which is the highest possible state for
unrecognized objects).
However, as outlined above, the MSH also predicts that the preference
for the object in a higher state should be stronger, the higher the
discrepancy between the memory states. While in recognition pairs the
maximal memory state distance can be observed (one object in
recognition certainty and the other in rejection certainty), in both
knowledge and guessing pairs this is assumed never to occur, since (to
a close approximation) objects will either be in the same state or in
adjacent states (recognition certainty and uncertainty or rejection
certainty and uncertainty, respectively). For this reason, we expect
weaker effects of recognition latency differences on choice
probabilities than those found for recognition cases. Additionally, we
will also test whether effects on choice probabilities are stronger
when the differences in latencies are higher, therefore increasing the
probability of the objects being in adjacent states versus in the same
state.
Note that the MSH prediction regarding knowledge cases overlaps with
what is called the fluency heuristic (Hertwig et al., 2008; Schooler and Hertwig, 2005). The fluency heuristic states that, in
knowledge cases, the fastest retrieved option should be chosen. Its
premise is that the fluency with which an object is retrieved from
memory (indexed by the latency of the recognition judgment) can be
used as a single cue and determine inferences. They measured the
accordance rate of the fluency heuristic by computing, for each
participant, how many times the object retrieved faster is chosen in
knowledge pairs (pairs with differences in recognition latency smaller
than 100 ms were excluded),2 and found it to be reliably higher
than the chance probability of .50. Furthermore, they observed that
accordance rates increase with the difference in latencies between
objects. While the fluency heuristic can accommodate these results,
its empirical scope is limited: It applies only to knowledge pairs,
and within those, to pairs where the fluency difference is larger than
100ms. The MSH, in contrast, predicts these and other results,
including predictions for guessing and recognition cases. It is,
therefore, a framework with a wider scope and more parsimonious than a
combination of different heuristics for knowledge, recognition, and
guessing cases (Erdfelder, Küpper-Tetzel and Mattern, 2011). Importantly, the MSH also
predicts that the preference for the faster recognized object in
knowledge cases should be considerably weaker than the preference for
recognized objects in recognition cases, simply because the
memory-state discrepancy for knowledge pairs can only be small (i.e.,
recognition certainty and uncertainty) or even nonexistent (i.e., when
both objects are in the same state). The fluency heuristic, in
contrast, is silent about the predicted effect size for knowledge
cases as compared with recognition cases. Notably, this MSH prediction
has already found some support in previous research
(e.g., Hilbig, Erdfelder and Pohl, 2011; Marewski and Schooler, 2011; Pohl et al., 2016; Schwikert and Curran, 2014).
While the predictions for knowledge cases seem plausible and
straightforward, the core prediction for guessing cases is more
surprising and counterintuitive as it conforms to the expectation of a
preference for less fluent objects. To the best of our knowledge, no
framework other than the MSH makes or can accommodate such a
prediction. Therefore, the most important focus of our first study
lies in the novel and apparently counterintuitive prediction for
guessing cases.
In addition to these predictions for knowledge and guessing cases, we
focus on a prediction of the MSH for recognition cases in a second
study. Erdfelder, Küpper-Tetzel and Mattern (2011) already showed that larger recognition
and rejection latencies are associated with weaker preferences for the
recognized object in recognition cases. In our second study, we aim to
conceptually replicate this result in a more refined way using a
better measure of MSH-use. The proportions of choices of the
recognized objects used by Erdfelder, Küpper-Tetzel and Mattern are biased
measures of MSH-use because counting the number of times choices are
in line with MSH use does not take into account what led to that
choice. An option might have been chosen because it was in a higher
memory state, or because other information, which points in the same
direction, was used. For example, when comparing supposed population
sizes of Berlin and Mannheim, a non-european person might chose Berlin
because she recognizes it with certainty and does not recognize
Mannheim, or because she knows Berlin is the capital of Germany, and
therefore likely to be a large city.
For this reason, Hilbig, Erdfelder and Pohl (2010) developed a multinomial
processing tree model which estimates RH-use in a more sophisticated
way. The r-model (Figure 2) consists of three trees, which
correspond to the three types of pairs. For knowledge and guessing
pairs, the trees have only a single parameter that accounts for the
accuracy for knowledge and guessing pairs, respectively. For
recognition pairs, on the other hand, the model considers the
possibility that a recognized option is chosen through use of further
knowledge, and provides in this way an unbiased estimate of RH-use
(which corresponds to parameter r in the model;
see Hilbig, Erdfelder and Pohl (2010) for addditional details about the r-model).
By adopting this model to measure MSH use for recognition cases, we
can assess in a more precise way how recognition and rejection
latencies are associated with noncompensatory reliance on
recognition. Additionally, we can test whether in the most extreme
cases, when the recognition judgment latencies are very short (so that
both objects are most likely in recognition and rejection certainty
states), people always rely on memory-states only, or whether even
then the probability of choosing the recognized object is
significantly smaller than one, suggesting that other processes such
as integration of further knowledge are involved in at least some of
the cases where conditions for relying on memory strength are optimal.
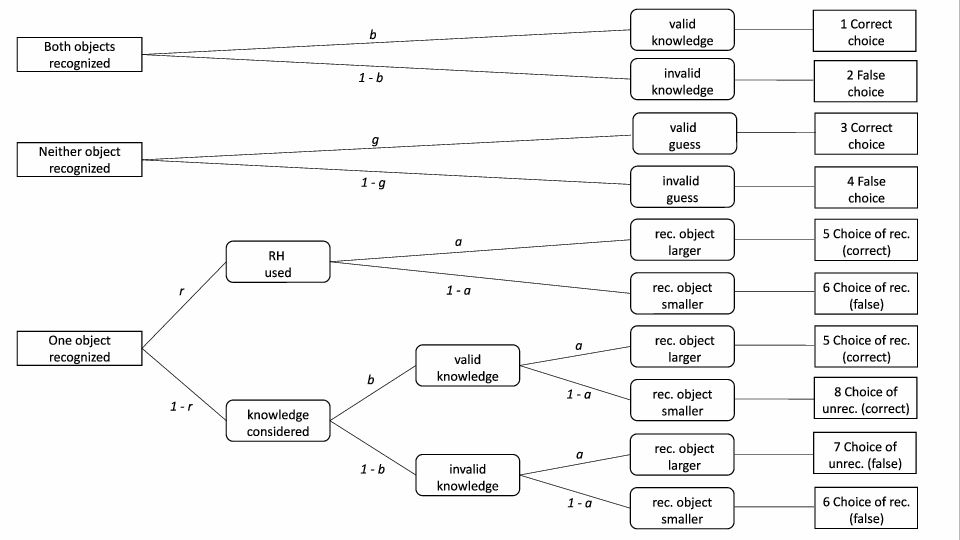
| Figure 2: Graphical representation of the r-model: Parameter r denotes the probability of applying the recognition heuristic as originally proposed, that is, by ignoring any knowledge beyond recognition. a = recognition validity (probability of the recognized object representing the correct choice in a recognition case); b = probability of valid knowledge; g = probability of a correct guess; rec. = recognized; unrec. = unrecognized. |
In general, since Horn, Pachur and Mata (2015) observed correlations above .90
between r parameter estimates and RH accordance rates, we expect
similar results for our second study as previously reported by
Erdfelder, Küpper-Tetzel and Mattern. However, the additional possibility to
assess the hypothesis r = 1 (i.e., perfect reliance on recognition)
for objects in memory certainty states renders use of the r-model
particularly attractive for our current study.
2 Study 1: MSH predictions for guessing and knowledge cases
We first tested whether choices for guessing and knowledge cases are
in accordance with the MSH prediction that there is a preference for
the object in a higher state. Specifically, as outlined above, we used
recognition and rejection latencies as proxies for underlying memory
states. Therefore, we predicted that in knowledge pairs there is a
preference for the object with a shorter recognition latency (and
therefore a higher probability of being in a recognition certainty
state) while in guessing pairs there is a preference for the object
with the longest rejection latency (and therefore a higher probability
of being in the uncertainty state).
2.1 Reanalysis of published data
We reanalyzed the data of 14 published data sets from our lab (Table
1), in order to look for preliminary evidence for our
hypotheses. As shown in Figure 3, we observed that for
all 14 data sets the proportion of choosing the object recognized
faster in knowledge cases was significantly larger than .5 (smallest
t(21) = 2.78, all p < .01). Regarding guessing cases, in 12 of the
14 data sets the proportion of choosing the object recognized more
slowly was significantly larger than .5 (smallest significant
t(63) = 2.08, p = .02). For comparison purposes, the accordance
rates for the RH (applying to recognition cases) are also included in
Figure 3, showing that choice preferences for
recognized objects in recognition cases are much stronger than choice
preferences in the other two cases.
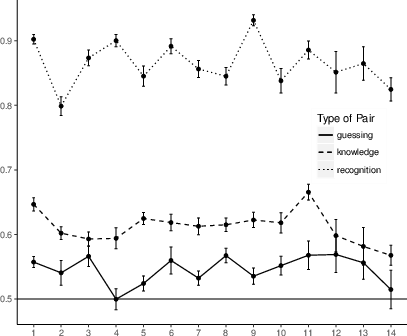
| Figure 3: Proportion of choices of the fastest or slowest
recognized or unrecognized object for knowledge and guessing
cases, respectively, and of the recognized object for
recognition cases, for all 14 reanalyzed datasets. Error
bars represent standard error of the mean. |
| Table 1: Source and description of the 14 reanalyzed data sets. |
| Data set | Origin | Materials and criterion | N |
| Michalkiewicz & Erdfelder (2016) | |
| 1 | Exp 1, first session | 100 of 150 largest US cities, size | 19200 |
| 2 | Exp 2, first session | 100 of 150 largest US cities, size | 24900 |
| 3 | Exp 3a | 25 of 100 most successful celebrities, size | 20400 |
| 4 | Exp 3b | 25 of 100 most successful german movies, size | 20400 |
| 5 | Exp 3c | 25 of 60 largest islands, size | 19200 |
| 6 | Exp 3d | 25 of 100 most successful musicians, size | 19200 |
| 7 | Exp 4a | 25 of 100 most successful celebrities, size | 26100 |
| 8 | Exp 4b | 25 of 100 most successful celebrities, pictures, size | 26100 |
| Michalkiewicz, Arden, & Erdfelder (2016) | |
| 9 | Exp 1a | 25 of 100 most successful celebrities, success | 13200 |
| Castela & Erdfelder (2017) | |
| 10 | Exp 1, first session | 80 of 150 largest US cities, size | 9360 |
| 11 | Exp 2, first session | 80 of 150 largest US cities, size | 7920 |
| Hilbig, Michalkiewicz, Castela, Pohl, & Erdfelder (2015) | |
| 12 | Exp 1, control group | 20 of 61 largest world cities, size | 4370 |
| 13 | Exp 2, control group | 20 of 61 largest world cities, size | 4180 |
| 14 | Exp 3, control group | 84 of 100 largest world cities, size | 2688 |
Clearly, these results are in line with our expectations. However, the
studies included in the reanalysis were not conducted with our
hypotheses in mind. In order to collect further evidence, we designed
a new experiment specifically tailored to our hypotheses. With this
new experiment, we primarily aimed at optimizing the proportion of
knowledge and guessing cases in order to achieve more powerful tests
of the MSH predictions for these cases. Moreover, we were also
interested in generalizing the results across different decision
domains beyond city-size comparisons.
2.2 Experiment 1
2.2.1 Material and procedure
The paradigm we used resembles the city-size paradigm outlined in the
section The Recognition Heuristic but involves different types
of decisions. This paradigm includes two tasks: (1) a recognition
test, where objects are presented and participants must judge whether
they have seen them before or not; (2) a comparison task, where
participants see pairs of the objects and must infer which scores
higher on a given criterion. Since the objects are paired
exhaustively, the relative proportion of knowledge, recognition, and
guessing cases will depend on the proportion of objects
recognized. Therefore, in order to optimize the proportion of
knowledge and guessing cases, it is important to include in the
experiment a condition for which the proportion of recognized objects
across participants is larger than .50 (resulting in many knowledge
cases) and a different condition in which the proportion of recognized
objects is clearly less than .50 (resulting in many guessing cases). A
third condition should involve a recognition rate of about .50,
resulting in (almost) equal frequencies of knowledge and guessing
cases. Moreover, since we also wanted to generalize our findings
across different domains, we made use of different types of objects
and inference criteria in the three conditions. Specifically, all
participants were presented with objects from three domains: largest
world cities (with over 3 million inhabitants;
http://en.wikipedia.org/wiki/List\_of\_cities\_proper\_by\_population),
most successful celebrities (100 most successful celebrities according
to the Forbes list of 2015; http://www.forbes.com) and longest
rivers in the world (over 1900 km long;
https://en.wikipedia.org/wiki/List\_of\_rivers\_by\_length). According
to pre-tests conducted in our lab, we know that for the domain of
world cities normally 50% of the objects are recognized. We included
this domain for purposes of generalization, and also because it is one
of the most often used domain in the study of the RH and should serve
as benchmark. For the domain of celebrities, normally 65% of the
objects are recognized. Therefore, this domain is ideal to test the
hypothesis regarding knowledge cases. Finally, the rivers domain is
ideal for testing the hypothesis regarding guessing cases, since
usually only 35% of the objects are recognized. The experiment
included three blocks, each consisting of the recognition test and the
comparison task for each domain.
The order of blocks was randomized for all participants. In each
block, the recognition test always preceded the comparison task. In
the recognition test participants saw all 20 objects (randomly
selected from each domain, but the same for all participants) and had
to decide whether they have heard of them before or not. Objects were
presented one at a time, in random order, and a 500 ms interstimulus
fixation-cross followed each response. Response times were recorded
along with the recognition judgments. After each recognition test, a
comparison task followed. In the comparison task, participants saw 190
pairs, consisting of the exhaustive pairing of the 20 objects, and had
to infer which one scored higher on the criterion. Each pair was
presented at a time, in random order, and a 500 ms interstimulus
fixation-cross followed each response. Response times were recorded
along with the responses. For the world cities, the criterion was
city-size; for celebrities, the criterion was how successful they
were3; and for the rivers, the criterion
was their length.
2.2.2 Participants
To provide an appropriate balance between type-1 and type-2 error
rates in χ 2 model tests (Erdfelder, 1984; Moshagen and Erdfelder, 2016), we recruited 75 students (50 women) from the
University of Mannheim aged between 19 and 46 years
(M = 22.00, SD = 5.04). Participation was compensated monetarily as
a function of performance in the comparison task. Every participant
received at least two euros, and they could earn up to 7.70. They
gained one cent for each correct answer, and lost one cent for each
wrong one.
2.2.3 Results
One participant had to be removed from the analysis for all domains,
because he indicated that he did not recognize any object in any
domain. Furthermore, one participant was removed from the guessing
analysis of the cities domain because he recognized 19 out of the 20
cities, therefore having no guessing pairs. Finally, two additional
participants were removed from the knowledge analysis of the rivers
domain because they only recognized one river and therefore had no
knowledge pairs. For the remaining participants, the proportion of
recognized items was on average .68 for celebrities, .58 for the world
cities, and .36 for rivers. This was in line with the pre-tests,
although a bit higher than what we expected for the world cities
domain.
Since our hypotheses refer to the preference for the object recognized
faster in knowledge pairs, and the one judged unrecognized more slowly
in guessing pairs, we first calculated per participant the proportion
of times their choices were in line with those hypotheses (accordance
rate). We then performed one-sample t-tests to assess whether the
mean accordance rates were larger than .50. As can be seen in Table
2, we found support for both hypotheses in all three
domains assessed. For comparison purposes, the accordance rates for
the RH are also included in Table 2, replicating the
previous result that choice preferences for recognized objects in
recognition cases are much stronger than the predicted choice
preferences for knowledge and guessing cases.
| Table 2: Experiment 1. Results of one-sample t-tests testing if the
mean of the individual proportion of choices in accordance with our
hypotheses is higher than .50. For knowledge cases, accordance means
choosing the fastest recognized object, for guessing cases
accordance means choosing the slowest unrecognized object, and for
recognition cases accordance means choosing the recognized
object. * significant at the .05 α level. |
| | Knowledge Cases | Guessing Cases | Recognition Cases |
| | Accordance | t | df | p | Accordance | t | df | p | Accordance | t | df | p |
| World Cities (size) | .60 | 8.28 | 73 | < .001* | .55 | 2.85 | 72 | < .01* | .83 | 20.6 | 73 | < .001* |
| Celebrities (success) | .60 | 7.78 | 73 | < .001* | .55 | 2.13 | 73 | .02* | .85 | 23.43 | 73 | .001* |
| Rivers (length) | .67 | 9.35 | 71 | < .001* | .54 | 3.53 | 73 | .001* | .81 | 19.88 | 73 | < .001* |
In addition to testing for an above chance preference for the items
more likely to be in a higher state, we also wanted to assess whether
this preference would increase with an increasing difference in
recognition latencies (i.e., latencies of yes judgments) or
rejection latencies (i.e., latencies of no judgments) between
objects in a pair (and therefore an increasingly higher probability of
being in adjacent states). To do so, we ran a multilevel logistic
regression4 (level 1: choices per participant; level 2:
participants) with Accordance as a dependent
variable. Accordance is essentially a binary variable which takes
the value one if choices are in line with our hypotheses, and zero
when they are not. Specifically, for knowledge pairs, Accordance
will be one whenever the fastest recognized object is chosen, and zero
otherwise. Conversely, for guessing pairs, Accordance will be one
whenever the slowest unrecognized object is chosen, and zero
otherwise. As predictors, we included both the main effects and the
interactions of the RT difference (difference in recognition or
rejection latencies between the objects in a pair) with Case
(knowledge or guessing) and with Domain (celebrities, cities or
rivers). Additionally, the model includes a random intercept for each
participant and a random slope for the effect of RT difference
within each participant. Our hypothesis would be that RT
difference has a positive effect on Accordance for both cases and
in all domains. We find support for our hypothesis.
As can be seen in Table 3, RT difference has a
significant positive effect on Accordance. Additionally, there are
no differences in Accordance between the domains.5 Moreover, while the effect is
present for both knowledge and guessing cases (Figure
4), we find that it is significantly stronger for
knowledge cases. While this was not directly predicted, it does not
compromise our findings. This will be addressed in more detail in the
Discussion section.
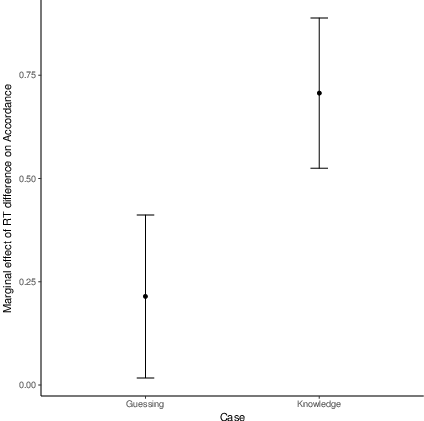
| Figure 4: Experiment 1. Marginal effect of RT difference on accordance for guessing and knowledge cases. Error bars represent 95% confidence intervals. |
| Table 3: Experiment 1. Summary of fixed effects results in multivel logistic regression showing how the difference in latencies between two objects in a pair (RT difference) predicts the accordance. Accordance is defined as choosing the fastest recognized object in knowledge cases, and the slowest recognized object in guessing cases. |
| Predictor | Coefficient | SE | z value | p |
| Intercept | 0.10 | 0.04 | 2.23 | .03* |
|
RT difference | 0.24 | 0.08 | 3.06 | < .01* |
| Case (Knowledge vs. Guessing) | 0.14 | 0.04 | 3.28 | < .01* |
| Domain Celebrities (vs. Cities) | 0.01 | 0.03 | 0.39 | .70 |
| Domain Rivers (vs. Cities) | .02 | 0.04 | 0.67 | .50 |
| RT difference x Case Knowledge (vs. Guessing) | 0.48 | 0.07 | 6.59 | < .001* |
For discrete predictors, information in parentheses clarifies the levels of the predictor which are being compared. The RT difference is scaled in seconds. * significant at the .05 α level.
|
3 Study 2: The influence of removing items with longer recognition/rejection judgment latencies on reliance on recognition
As mentioned above, in our second study we wanted to test the MSH
predictions regarding recognition judgment latencies for recognition
cases. Similar predictions were previously tested by
Erdfelder, Küpper-Tetzel and Mattern (2011), but by relying on accordance rates only. The
core question of our second study is whether we can replicate their
results using the r parameter of the r-model as a more refined proxy
for MSH use (Hilbig, Erdfelder and Pohl, 2010). Specifically, we aimed to test
whether there is an increase in r when we sequentially remove items
with longer recognition and rejection latencies and fit the r-model to
those subsets of data.6 The rationale behind this is that by removing
those “slow” items we reduce the subset mostly to objects in
recognition certainty and rejection certainty states. By doing so
successively, we artificially create the perfect preconditions for
relying uniquely on recognition, which should lead to increasingly
higher r estimates. If this prediction holds, an interesting further
question to pursue is to what degree r estimates approximate 1
(i.e. perfect reliance on recognition in paired comparison judgments)
if the subset is reduced to objects with the fastest yes or no
recognition judgments only.
3.1 Reanalysis of published data
To address these questions, we first reanalyzed the data for the 14
published data sets that we used in our previous reanalysis
(Table 1). For each data set, we first identified for each
participant which items where in the first, second, third or fourth
quartile of their individual recognition and rejection latency
distributions. In a second step, we created (at the aggregate
level)7 four subsets of pairs
that consisted only of objects with latencies in each of the quartiles
of the latency distributions.8 Next, we fitted the
r-model simultaneously to these four disjoint subsets of data by
replicating the r-model trees four times, that is, for each subset of
pairs. By implication, we ended up with four r estimates. At the
level of parameters, our hypothesis can be described as an order
restriction such that the r parameters decrease from r1 to r4,
with the index 1 corresponding to the first quartile of the
distribution (only the fastest recognized and unrecognized objects are
included) and 4 the last quartile of the distribution (only the
slowest recognized and unrecognized objects are included).
All model-based analyses were performed with MPTinR
(Singmann and Kellen, 2013) in R (Team, 2015). We first fitted the model
without any restrictions; this baseline model fits the data well for 9
of the 14 data sets (Table 4). To test our hypothesis, we
excluded the 5 data sets that were associated with misfit.9 To evaluate our order restriction we
need two tests. First, we test the order restriction,
r1 ≥ r2 ≥ r3 ≥ r4, against the baseline model (with no
restriction on the four r parameters). Second, we test the model
with order restrictions, r1 ≥ r2 ≥ r3 ≥ r4, against a
model imposing equality restrictions, r1 = r2 = r3 = r4. If the
order restriction corresponds to the most suitable version of the
model, the first test should fail to reach statistical significance,
while the second test should lead to statistically significant
results.
| Table 4: Goodness-of-fit statistics, corresponding degrees of freedom, and p-values for all reanalyzed data sets and Experiment 2. |
| Data Set | G2 | df | p-value |
| 1 | 10.35 | 4 | .03* |
| 2 | 3.87 | 4 | .42 |
| 3 | 10.58 | 4 | .03* |
| 4 | 9.22 | 4 | .06 |
| 5 | 2.51 | 4 | .64 |
| 6 | 0.50 | 4 | .97 |
| 7 | 10.85 | 4 | .03* |
| 8 | 2.74 | 4 | .60 |
| 9 | 4.53 | 4 | .34 |
| 10 | 9.97 | 4 | .04* |
| 11 | 4.62 | 4 | .33 |
| 12 | 12.03 | 4 | .02* |
| 13 | 5.22 | 4 | .27 |
| 14 | 0.79 | 4 | .94 |
| Exp 2 | 7.44 | 4 | .11 |
* indicates that the baseline model does not fit the data well, leading to statiscally significant misfit. |
| Table 5: Maximum likelihood parameter estimates of all r parameters and p-values and differences in FIA for comparisons between the baseline model and the order-restriced model (BO) and between the order-restricted and the equality-restricted model (OE) for all reanalyzed data sets and Experiment 2. |
| Data set | r1 | r2 | r3 | r4 | pBO | pOE | ΔFIABO | ΔFIAOE | N |
| 2 | .71 (.03) | .66 (.03) | .59 (.04) | .46 (.03) | 1 | 0 | 3.18 | -16.44 | 5521 |
| 4 | .86 (.02) | .83 (.03) | .73 (.03) | .70 (.03) | 1 | 0 | 3.18 | -9.18 | 4526 |
| 5 | .82 (.02) | .68 (.03) | .58 (.04) | .51(.03) | 1 | 0 | 3.17 | -25.41 | 4260 |
| 6 | .89 (.02) | .83 (.03) | .71 (.04) | .60 (.03) | 1 | 0 | 3.18 | -28.22 | 4264 |
| 8 | .78 (.02) | .74 (.03) | .62 (.03) | .51 (.03) | 1 | 0 | 3.17 | -27.73 | 5793 |
| 9 | .93 (.02) | .91 (.02) | 86 (.03) | .71 (.04) | 1 | 0 | 3.18 | -16.69 | 2929 |
| 11 | .85 (.04) | .85 (.04) | .69 (.05) | .55 (.06) | .41 | 0 | 3.18 | -11.26 | 1907 |
| 13 | .82 (.05) | .67 (.08) | .63 (.09) | .50 (.07) | 1 | < .01 | 3.18 | -3.97 | 902 |
| 14 | .73 (.13) | .64 (.15) | 1 (.55) | .33 (.17) | .05 | .03 | 0.61 | -3.55 | 304 |
| Exp 2 | .70 (.01) | .65 (.02) | .64(.02) | .47 (.02) | 1 | 0 | 3.18 | -53.25 | 21456 |
Since our hypothesis involves an order restriction between four
parameters, the sampling distribution of the likelihood-ratio test
statistic Δ G2 does not follow a default χ 2
distribution with the appropriate degrees of freedom. Given the
challenge involved in determining the appropriate distribution, we
opted for using a double bootstrap method (Van De Schoot, Hoijtink and Deković, 2010) to
compute p-values. For example, when we want to test the order
restrictions, r1 ≥ r2 ≥ r3 ≥ r4, against the baseline
model, the double bootstrap consists of the following steps: (1) a
non-parametric bootstrap sample is obtained from a given data set; (2)
the model imposing the null hypothesis,
r1 ≥ r2 ≥ r3 ≥ r4, is fitted to that data set; (3)
those parameter estimates are used to obtain a parametric bootstrap
sample; (4) both models under scrutiny (i.e., the model imposing the
order restriction r1 ≥ r2 ≥ r3 ≥ r4 and the baseline
model) are fitted to that sample and the difference in fit is
calculated; (5) steps 1 to 4 are repeated many times (we repeated it
1000 times). We then compute the p-value by assessing how many
times the difference in fit obtained with the bootstrapped samples is
equal or more extreme than the difference in fit obtained with the
original data set, and reject the null hypothesis if this proportion
is smaller than .05. Additionally, we also compare the models through
the model selection measure FIA (Fisher Information Approximation),
which takes complexity into account.10
The results are shown in Table 5 and Figure
5. We find a clear support for the order-restricted
model both with the goodness-of-fit test and the FIA
comparison.11 In all except one data set
(Data Set 14) the order restriction did not lead to significant
misfit, while the equality restriction did. In line with these
results, FIA was smaller for the order restricted model than for the
baseline or the equality restricted model. Only for Data Set 14, in
line with the results from the goodness-of-fit test, the difference in
FIA between the baseline and the order restricted model is not
sufficient to support the former.
Additionally, to test whether r approaches one, we looked at the
95% confidence interval of the r1 probability estimates. For all 9
data sets this confidence interval does not include 1, suggesting that
even under ideal conditions for use of memory state information alone
people still sometimes rely on other strategies, like use of further
knowledge.
While these results lend support to our hypothesis, the re-analyses
are not ideal because, when creating the subsets of pairs, we
necessarily limit the data points available for analysis (Table
5). Therefore, we designed Experiment 2 with the goal
of testing our hypothesis with greater power.
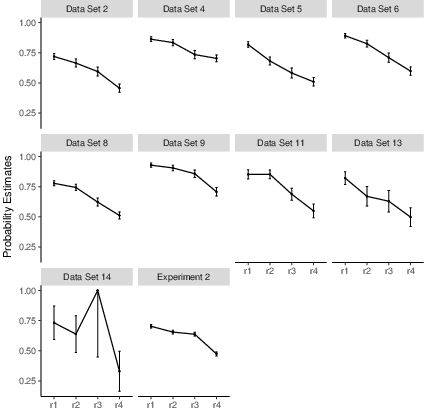
| Figure 5: r probability estimates in all four quartiles of recognition and rejection latency distributions for all reanalyzed datasets and for Experiment 2. Error bars represent standard errors. |
3.2 Experiment 2
3.2.1 Participants
To provide an appropriate balance between type-1 and type-2 error
rates in χ 2 model tests (Erdfelder, 1984; Moshagen and Erdfelder, 2016), we recruited 52 students (35 women) from the
University of Mannheim aged between 18 and 45
(M = 22.38, SD = 5.49). Participation was rewarded either with a
monetary compensation (2 euros) or with study participation
credits. Additionally, for each correct response in the comparison
task, participants gained 2.5 cents, and for each incorrect response
they lost 2.5 cents.
3.2.2 Material and procedure
The experiment consisted of the city-size paradigm, involving two
tasks. First, participants had a recognition task, where they saw 60
city names and had to indicate whether they recognize them or
not. Naturally, response times were recorded along with the
recognition judgments. The 60 cities were a random selection from the
largest world cities (with over 3 million inhabitants;
http://en.wikipedia.org/wiki/List\_of\_cities\_proper\_by\_population). After
the recognition task, cities were paired according to their
recognition and rejection latencies, with the cities having similar
recognition or rejection latencies assigned to the same set. More
precisely, there were four subsamples of pairs, created according to
the corresponding four bins of individual recognition and rejection
latencies. Whenever the number of recognized objects (or the
corresponding number of objects judged unrecognized) was not divisible
by four, it was randomly decided which bin(s) would have one object
more than the other(s). After the pairs were created (the number of
pairs across the four sets varied between participants, being either
420, 421 or 422), participants saw them and had to decide for each
pair which city was more populous. As in the analysis of published
data sets, a pair of cities was considered for subsequent analysis
only when (a) one city was recognized and the other was not and (b)
the corresponding individual recognition and rejection latencies fell
in the same quartile of the response time distribution.
3.2.3 Results
Before fitting the model, we removed one participant because he
recognized only one of the 60 cities, while the remaining participants
recognized on average 57% of the objects. With the data from the
remaining 51 participants, we determined the frequencies for each
category of the model, separately for the four bins of data. Then, we
fitted the r-model to the four bins of data. The model performed well
in describing the data (G2(4) = 7.44, p = .11, FIA = 65.49). We
repeated the same analysis that we performed with the published data
sets, with the goal of testing our order hypothesis on the parameters
r1 to r4. As can be seen in Table 5 and Figure
5, we again found support for our
hypothesis.12 Additionally, the
95% confidence interval of the probability estimates of r1 did not
include 1, which again shows that even under ideal conditions for
reliance on memory states alone, other strategies than mere reliance
on memory strength take place.
4 Discussion
When they introduced the MSH, Erdfelder, Küpper-Tetzel and Mattern (2011) contributed to
the RH literature by providing an extension of the heuristic that
parsimoniously links it with the recognition memory literature. The
MSH not only explains a lot of previously problematic results but also
provides a set of new predictions. While Erdfelder, Küpper-Tetzel and Mattern (2011),
Castela et al. (2014), and Castela and Erdfelder (2017) tested several
of these predictions and already gathered some support for the MSH, a
crucial additional empirical prediction regarding decisions between
pairs of unrecognized objects (“guessing cases”) has not been
addressed so far. Our primary aim was to close this gap and, in
addition, to provide further evidence on MSH predictions regarding
pairs of recognized objects (“knowledge cases”) and mixed pairs of one
recognized and one unrecognized object (“recognition cases”),
conceptually replicating and extending previously published results on
recognition judgment latency effects in binary decisions. We addressed
both of these issues in two studies by reanalyzing previously
published data sets and conducting two new experiments. In this way,
we found strong converging evidence in line with the MSH.
In our first study, by relying on recognition and rejection latencies
as a proxy for memory states — under the assumption that longer
latencies are associated with the uncertainty memory state while
shorter latencies are associated with certainty states — we found
evidence for the MSH prediction that for knowledge and guessing cases
people also have a preference for objects that are likely to be in a
higher memory state. While for knowledge cases the MSH prediction
overlaps with predictions of the fluency heuristic
(Hertwig et al., 2008), the prediction regarding guessing cases cannot
be accounted by any other framework we are aware of. Furthermore, that
latter prediction is quite counterintuitive, since it maintains that
objects recognized more slowly, and thus judged less fluently, should
be preferred in guessing cases. Obviously, this prediction conflicts
with the popular notion that cognitive fluency boosts choice
preferences (e.g. Schooler and Hertwig, 2005; Zajonc, 1968). Nevertheless, we
found unequivocal evidence for our prediction.13
It is also important to note that the MSH not only captures the
preference effects for knowledge and guessing cases correctly, but
also predicts they should be much smaller than the corresponding
effects in recognition cases. This is due to the fact that, in
knowledge and guessing pairs, the objects can only be either in the
same memory state or in adjacent memory states. Therefore, the
preference for the object in a higher state should be less marked than
in cases where the distance between states is maximal (pairs of one
object in recognition certainty and one object in rejection
certainty), a combination that can only occur for recognition
pairs. Note that this prediction cannot be derived from the fluency
heuristic theory (Schooler and Hertwig, 2005), simply because the latter
considers knowledge cases in isolation. Hence, the MSH theory not only
makes more predictions than the fluency heuristic theory, it also
makes more precise (or “specific”) predictions. In other words, the
MSH theory has larger empirical content (in the Popperian sense)
compared to the latter theory (Glöckner and Betsch, 2011, see, e.g.,). We thus believe the MSH presents
itself as the most parsimonious framework for understanding how
recognition is used in binary inferences, clearly outperforming other
heuristic-based approaches, like the RH and the fluency heuristic, in
its explanatory power, empirical content, and empirical scope.
One result worth noting is that the effect of latencies was stronger
for knowledge cases than for guessing cases. While we had not
predicted this explicitly, it fits nicely with previous
results. Specifically, Castela and Erdfelder (2017) observed that
MSH-use is higher for recognition pairs if one object is in
recognition certainty and one object in the uncertainty state than for
recognition pairs with one object in uncertainty and one object in the
rejection certainty state. Since these are the memory state
combinations that can underlie adjacent state cases within knowledge
and guessing pairs, respectively, our current results seem to be
exactly in line with what was found by Castela and Erdfelder
— a stronger tendency to use the MSH in the former cases. Given the
converging evidence concerning this effect, future studies should
focus on testing possible explanations for it. One such explanation,
already suggested by Castela and Erdfelder, is that the
effective distance in memory strength between the recognition
certainty and uncertainty memory states might be larger than the
corresponding difference between the uncertainty and rejection
certainty memory states. This would suggest that a simple ordinal
description of the states might be insufficient.
With our second study, we aimed at further testing the effect of
recognition and rejection latencies on choices for recognition
pairs. While this is largely a conceptual replication of the test
carried out by Erdfelder, Küpper-Tetzel and Mattern (2011), we relied on a different
measure of RH-use, which we believe is more
adequate. Erdfelder, Küpper-Tetzel and Mattern relied on accordance rates
which, as explained above, are a confounded measure, since people might
choose the recognized option for reasons other than reliance on
recognition, namely because they rely on further knowledge. For this
reason, Hilbig, Erdfelder and Pohl (2010) proposed the r-model, and specifically
the r parameter of the model, as a better measure. The main
advantage is that the r-model disentangles choices of the recognized
option that originate from reliance on recognition from the ones
stemming from use of further knowledge. Extending the scope of tests
previously carried out by Erdfelder, Küpper-Tetzel and Mattern (2011), we additionally
investigated the prediction that MSH-use as indexed by the r
parameter should increase the shorter the recognition and rejection
latencies of objects in a pair. We found support for this hypothesis
by reanalyzing 9 data sets and, in addition, with a new experiment
tailored exactly to this test. Furthermore, we assessed whether in the
most extreme cases, that is, when the recognition and rejection
latencies were shortest and therefore the probabilities that both
objects are in recognition and rejection certainty states were
highest, MSH-use would be the only strategy used. The 95% confidence
intervals for the corresponding r1 parameter estimates did not
include 1 in any of our data sets, suggesting that this is not the
case. Hence, even under perfect conditions for relying on memory
strength, people will sometimes resort to other inference strategies
and integrate further knowledge. Overall, our results are in stark
conflict with the recognition heuristic (RH) theory as originally
proposed by Goldstein and Gigerenzer (2002) and in line with the MSH theory.
Recently, Heck and Erdfelder (2017) also criticized the RH framework,
but from a different perspective than the MSH framework does. It thus
seems worthwhile to consider their work in a bit more detail and
compare it with our current work. Using an extension of Hilbig et
al.’s r-model to response times as an innovative measurement model,
Heck and Erdfelder (2017) showed that the decision latency predictions
of the RH are in conflict with virtually all available data on RH use
in natural decision domains. Only a small proportion of individual
data sets could be adequately described by a serial RH theory
according to which recognition vs. non-recognition is considered as
the first cue in binary decisions with probability r, possibly
followed by consideration of further knowledge about the recognized
object with probability 1−r. The vast majority of individual
decisions could be described better by an information integration
account as formalized in the parallel constrained satisfaction (PCS)
model advocated by Glöckner and Betsch
( 2008; see also Glöckner and Bröder, 2011, 2014, and Glöckner, Hilbig and Jekel, 2014). According
to the PCS account, the recognition cue and further knowledge cues are
always considered simultaneously, resulting in fastest decisions when
all cues are congruent, that is, when both recognition and further
knowledge suggest the choice of the same object.
What are the implications of Heck and Erdfelder (2017) work for MSH
research as addressed in the current paper? An immediate implication
is that the r parameter of the r-model should not be interpreted as
the probability of applying a serial heuristic as presented by
Goldstein and Gigerenzer (2002) or as part of the take-the-best heuristic that
considers recognition always as the first cue in binary decisions
(Gigerenzer and Goldstein, 1996). This is unproblematic for our current work since we
consider r as a proxy for use of the MSH in which the order of cue
processing is left unspecified. In our application, r just
represents the probability of noncompensatory reliance on recognition
in the sense that the influence of recognition dominates the joint
influence of all further knowledge cues. Note that this is not in
conflict with a parallel information integration account, as the weight
of recognition in a PCS model can be so high that the influence of
recognition cannot be overruled by any combination of other decision
cues with (much) smaller weights. Thus, the r parameter of
Hilbig, Erdfelder and Pohl’s (2010) r-model (and also
the corresponding parameter of the r-s-model, cf. Hilbig et al., 2011)
can still be interpreted as a measure of noncompensatory reliance on
recognition if noncompensatory reliance on recognition is not
confused with reliance on recognition alone (i.e., as a serial
cognitive strategy predicted by the RH theory).
Now let us consider the reverse question: What are the implications of
our current MSH research for the PCS model of recognition-based
decisions advanced by Heck and Erdfelder (2017)? In fact, the latter
model shares one weakness with the RH theory, namely, that recognition
is considered as a binary cue only. Although this simple parallel
model suffices to explain a number of results that the RH cannot
explain (as shown by Heck and Erdfelder), it has
difficulties in explaining some of the results that the MSH can account
for. For example, we cannot see how to explain the choice preference
for the object judged unrecognized more slowly in guessing pairs using
a PCS model with only a single dichotomous recognition cue as assumed
in Heck and Erdfelder (2017, p. 446, Fig. 2). If anything, then such a
PCS model would need to be extended to include several nodes
representing differences in recognition information. For the time
being, however, the MSH appears to be the only model that captures the
preference for the option judged unrecognized more slowly. Recall also
that Castela et al. (2014) found a preference for choices of
recognized objects for which participants reported having further
knowledge as compared to objects judged merely recognized. This result
is predicted by the MSH (assuming that virtually all objects with
further knowledge are in the recognition certainty state), whereas it
poses difficulties for information integration accounts like PCS. For
fixed weights of the cues this model would predict more reliance on
recognition when further knowledge other than recognition is not
readily available.14
In sum, with our work we tried to answer questions left open by
Castela et al. (2014), Castela and Erdfelder (2017), and
Erdfelder, Küpper-Tetzel and Mattern (2011), thereby accumulating further support for the
MSH. We believe we achieved this goal in two different ways: First and
primarily, by finding support for its bold predictions for guessing
cases and in this way showing how it can parsimoniously explain a much
larger chunk of data than the RH or the fluency heuristic can; second,
by conceptually replicating and finding converging support for its
predictions regarding knowledge and recognition cases that have larger
empirical content than those derived from the RH or the fluency
heuristic. Finally, our results also show that while the MSH appears
to be a more useful framework than the RH, it should not be understood
in a deterministic way, since even when the objects are (likely to be)
in the two extreme memory states — recognition certainty and
rejection certainty — people sometimes resort to strategies other
than choosing the option in a higher memory state.
References
-
-
Anderson, J. R., Bothell, D., Lebiere, C., and Matessa, M. (1998).
An integrated theory of list memory.
Journal of Memory and Language, 38(4):341--380.
[ bib ]
-
-
Batchelder, W. H. and Riefer, D. M. (1999).
Theoretical and empirical review of multinomial process tree
modeling.
Psychonomic Bulletin & Review, 6(1):57--86.
[ bib ]
-
-
Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015).
Fitting linear mixed-effects models using lme4.
Journal of Statistical Software, 67(1):1--48.
[ bib ]
-
-
Bröder, A. and Eichler, A. (2006).
The use of recognition information and additional cues in inferences
from memory.
Acta Psychologica, 121(3):275--284.
[ bib ]
-
-
Bröder, A., Kellen, D., Schütz, J., and Rohrmeier, C. (2013).
Validating a two-high-threshold measurement model for confidence
rating data in recognition.
Memory, 21(8):916--944.
[ bib ]
-
-
Castela, M. and Erdfelder, E. (2016).
Further evidence for the memory state heuristic: Latency
predictions from binary inferences.
[ bib ]
-
-
Castela, M. and Erdfelder, E. (2017).
The memory state heuristic: A formal model based on repeated
recognition judgments.
Journal of Experimental Psychology: Learning, Memory &
Cognition, 43:205--225.
[ bib ]
-
-
Castela, M., Kellen, D., Erdfelder, E., and Hilbig, B. E. (2014).
The impact of subjective recognition experiences on recognition
heuristic use: A multinomial processing tree approach.
Psychonomic Bulletin & Review, 21(5):1131--1138.
[ bib ]
-
-
Cohen, J. (1988).
Statistical power analysis for the behavioral sciences.
Hillsdale, NJ: Erlbaum, 2 edition.
[ bib ]
-
-
Conrey, F. R., Sherman, J. W., Gawronski, B., Hugenberg, K., and Groom, C. J.
(2005).
Separating multiple processes in implicit social cognition: the quad
model of implicit task performance.
Journal of personality and social psychology, 89(4):469.
[ bib ]
-
-
Coolin, A., Erdfelder, E., Bernstein, M. D., Thornton, A. E., and Thornton,
W. L. (2015).
Explaining individual differences incognitive processes underlying
hindsight bias.
Psychonomic Bulletin & Review, 22:328--348.
[ bib ]
-
-
Dougherty, M. R., Franco-Watkins, A. M., and Thomas, R. (2008).
Psychological plausibility of the theory of probabilistic mental
models and the fast and frugal heuristics.
Psychological review, 115(1):199.
[ bib ]
-
-
Erdfelder, E. (1984).
Zur Bedeutung und Kontrolle des !B-Fehlers bei der
inferenzstatistischen Prüfung log-linearer Modelle [On significance
and control of the beta error in statistical tests of log-linear models].
Zeitschrift für Sozialpsychologie, 15:18--32.
[ bib ]
-
-
Erdfelder, E., Auer, T.-S., Hilbig, B. E., Aßfalg, A., Moshagen, M., and
Nadarevic, L. (2009).
Multinomial processing tree models: A review of the literature.
Zeitschrift für Psychologie/Journal of Psychology,
217(3):108--124.
[ bib ]
-
-
Erdfelder, E., Castela, M., Michalkiewicz, M., and Heck, D. W. (2015).
The advantages of model fitting compared to model simulation in
research on preference construction.
Frontiers in psychology, 6.
[ bib ]
-
-
Erdfelder, E., Küpper-Tetzel, C. E., and Mattern, S. D. (2011).
Threshold models of recognition and the recognition heuristic.
Judgment and Decision Making, 6(1):7--22.
[ bib ]
-
-
Faul, F., Erdfelder, E., Buchner, A., and Lang, A.-G. (2009).
Statistical power analyses using G* Power 3.1: Tests for
correlation and regression analyses.
Behavior Research Methods, 41(4):1149--1160.
[ bib ]
-
-
Faul, F., Erdfelder, E., Lang, A.-G., and Buchner, A. (2007).
G*power 3: A flexible statistical power analysis program for the
social, behavioral, and biomedical sciences.
Behavior Research Methods, 39(2):175--191.
[ bib ]
-
-
Gaissmaier, W. and Schooler, L. J. (2008).
The smart potential behind probability matching.
Cognition, 109(3):416--422.
[ bib ]
-
-
Gigerenzer, G. and Goldstein, D. G. (1996).
Reasoning the fast and frugal way: Models of bounded rationality.
Psychological Review, 103(4):650--669.
[ bib ]
-
-
Gigerenzer, G. and Goldstein, D. G. (2011).
The recognition heuristic: A decade of research.
Judgment and Decision Making, 6(1):100--121.
[ bib ]
-
-
Gigerenzer, G., Hoffrage, U., and Goldstein, D. G. (2008).
Fast and frugal heuristics are plausible models of cognition: Reply
to dougherty, franco-watkins, and thomas (2008).
11(1):230--239.
[ bib ]
-
-
Glöckner, A. and Betsch, T. (2008).
Modeling option and strategy choices with connectionist networks:
Towards an integrative model of automatic and deliberate decision making.
Judgment and Decision Making, 3:215--228.
[ bib ]
-
-
Glöckner, A. and Betsch, T. (2011).
The empirical content of theories in judgment and decision making:
Shortcomings and remedies.
Judgment and Decision Making, 6(8):711 -- 721.
[ bib ]
-
-
Glöckner, A. and Bröder, A. (2011).
Processing of recognition information and additional cues: A
model-based analysis of choice, confidence, and response time.
Judgment and Decision Making, 6(1):23--42.
[ bib ]
-
-
Glöckner, A. and Bröder, A. (2014).
Cognitive integration of recognition information and additional cues
in memory-based decisions.
Judgment and Decision Making, 9(1):35--50.
[ bib ]
-
-
Glöckner, A., Hilbig, B. E., and Jekel, M. (2014).
What is adaptive about adaptive decision making? A parallel
constraint satisfaction account.
Cognition, 133(3):641--666.
[ bib ]
-
-
Goldstein, D. G. and Gigerenzer, G. (1999).
The recognition heuristic: How ignorance makes us smart.
In Gigerenzer, G., Todd, P. M., and the ABC Research Group, editors,
Simple heuristics that make us smart, pages 37--58. Oxford University
Press.
[ bib ]
-
-
Goldstein, D. G. and Gigerenzer, G. (2002).
Models of ecological rationality: The recognition heuristic.
Psychological Review, 109(1):75--90.
[ bib ]
-
-
Heck, D. W. and Erdfelder, E. (2016).
Extending multinomial processing tree models to measure the relative
speed of cognitive processes.
Psychonomic Bulletin & Review, 23(5):1440--1465.
[ bib ]
-
-
Heck, D. W. and Erdfelder, E. (2017).
Linking process and measurement models of recognition-based
decisions.
Psychological Review, 124(4):442--471.
[ bib ]
-
-
Heck, D. W., Moshagen, M., and Erdfelder, E. (2014).
Model selection by minimum description length: Lower-bound sample
sizes for the Fisher Information Approximation.
Journal of Mathematical Psychology, 60:29--34.
[ bib ]
-
-
Hertwig, R., Herzog, S. M., Schooler, L. J., and Reimer, T. (2008).
Fluency heuristic: A model of how the mind exploits a by-product of
information retrieval.
Journal of Experimental Psychology: Learning, Memory, and
Cognition, 34(5):1191--1206.
[ bib ]
-
-
Hilbig, B. E. (2010).
Reconsidering “evidence” for fast-and-frugal heuristics.
Psychonomic Bulletin & Review, 17(6):923--930.
[ bib ]
-
-
Hilbig, B. E., Erdfelder, E., and Pohl, R. F. (2010).
One-reason decision making unveiled: A measurement model of the
recognition heuristic.
Journal of Experimental Psychology: Learning, Memory, and
Cognition, 36(1):123--134.
[ bib ]
-
-
Hilbig, B. E., Erdfelder, E., and Pohl, R. F. (2011).
Fluent, fast, and frugal? A formal model evaluation of the
interplay between memory, fluency, and comparative judgments.
Journal of Experimental Psychology: Learning, Memory, and
Cognition, 37(4):827--839.
[ bib ]
-
-
Hilbig, B. E., Michalkiewicz, M., Castela, M., Pohl, R. F., and Erdfelder, E.
(2015).
Whatever the cost? Information integration in memory-based
inferences depends on cognitive effort.
Memory & Cognition, 43(4):659--671.
[ bib ]
-
-
Hilbig, B. E. and Pohl, R. F. (2008).
Recognizing users of the recognition heuristic.
Experimental Psychology, 55(6):394--401.
[ bib ]
-
-
Hilbig, B. E. and Pohl, R. F. (2009).
Ignorance-versus evidence-based decision making: A decision time
analysis of the recognition heuristic.
Journal of Experimental Psychology: Learning, Memory, and
Cognition, 35(5):1296--1305.
[ bib ]
-
-
Hilbig, B. E., Pohl, R. F., and Bröder, A. (2009).
Criterion knowledge: A moderator of using the recognition heuristic?
Journal of Behavioral Decision Making, 22(5):510--522.
[ bib ]
-
-
Hintzman, D. L. (1988).
Judgments of frequency and recognition memory in a multiple-trace
memory model.
Psychological review, 95(4):528--551.
[ bib ]
-
-
Horn, S. S., Pachur, T., and Mata, R. (2015).
How does aging affect recognition-based inference? A hierarchical
bayesian modeling approach.
Acta psychologica, 154:77--85.
[ bib ]
-
-
Iverson, G. J. (2006).
An essay on inequalities and order-restricted inference.
Journal of Mathematical Psychology, 50(3):215--219.
[ bib ]
-
-
Kellen, D. and Klauer, K. C. (2015).
Signal detection and threshold modeling of confidence-rating rocs: A
critical test with minimal assumptions.
Psychological review, 122(3):542--557.
[ bib ]
-
-
Kellen, D. and Klauer, K. C. (in press).
Elementary signal detection and threshold theory.
In Wagenmakers, E.-J., editor, Stevens’ handbook of
experimental psychology and cognitive neuroscience, fourth edition (vol.
V). John Wiley & Sons, Inc, New York.
[ bib ]
-
-
Kellen, D., Klauer, K. C., and Bröder, A. (2013).
Recognition memory models and binary-response ROCs: A comparison by
minimum description length.
Psychonomic Bulletin & Review, 20(4):693--719.
[ bib ]
-
-
Kelley, C. M. and Jacoby, L. L. (2000).
Recollection and familiarity.
In E.Tulving and Craik, F. I. M., editors, The Oxford handbook
of memory. Oxford University Press.
[ bib ]
-
-
Klauer, K. C. (2010).
Hierarchical multinomial processing tree models: A latent-trait
approach.
Psychometrika, 75(1):70--98.
[ bib ]
-
-
Kuznetsova, A., Bruun Brockhoff, P., and Haubo Bojesen Christensen, R.
(2016).
lmerTest: Tests in Linear Mixed Effects Models.
R package version 2.0-30.
[ bib |
http ]
-
-
Macmillan, N. A. and Creelman, C. D. (2004).
Detection theory: A user's guide.
Psychology Press.
[ bib ]
-
-
Marewski, J. N., Gaissmaier, W., Schooler, L. J., Goldstein, D. G., and
Gigerenzer, G. (2010).
From recognition to decisions: Extending and testing
recognition-based models for multialternative inference.
Psychonomic Bulletin & Review, 17(3):287--309.
[ bib ]
-
-
Marewski, J. N. and Schooler, L. J. (2011).
Cognitive niches: An ecological model of strategy selection.
Psychological Review, 118(3):393--437.
[ bib ]
-
-
Matôt, S., Schreij, D., and Theeuwes, J. (2012).
Opensesame: An open-source, graphical experimental bulder for the
social sciences.
Behavior Research Methods, 44(2):314--324.
[ bib ]
-
-
Matzke, D., Dolan, C. V., Batchelder, W. H., and Wagenmakers, E.-J. (2015).
Bayesian estimation of multinomial processing tree models with
heterogeneity in participants and items.
Psychometrika, 80(1):205--235.
[ bib ]
-
-
Michalkiewicz, M. (2016).
Assessing and explaining individual differences within the
adaptive toolbox framework: New methodological and empirical approaches to
the recognition heuristic.
PhD thesis, University of Mannheim.
[ bib ]
-
-
Michalkiewicz, M., Arden, K., and Erdfelder, E. (2017).
Do smarter people make better decisions? The influence of
intelligence on adaptive use of the recognition heuristic.
Journal of Behavioral Decision Making.
[ bib |
DOI ]
-
-
Michalkiewicz, M. and Erdfelder, E. (2016).
Individual differences in use of the recognition heuristic are stable
across time, choice objects, domains, and presentation formats.
Memory & Cognition, 44(3):454--468.
[ bib ]
-
-
Moshagen, M. and Erdfelder, E. (2016).
A new strategy for testing structural equation models.
Structural Equation Modeling: A Multidisciplinary Journal,
23(1):54--60.
[ bib ]
-
-
Newell, B. R. and Fernandez, D. (2006).
On the binary quality of recognition and the inconsequentiality of
further knowledge: Two critical tests of the recognition heuristic.
Journal of Behavioral Decision Making, 19(4):333--346.
[ bib ]
-
-
Newell, B. R. and Shanks, D. R. (2004).
On the role of recognition in decision making.
Journal of Experimental Psychology: Learning, Memory, and
Cognition, 30(4):923.
[ bib ]
-
-
Pachur, T. (2011).
The limited value of precise tests of the recognition heuristic.
Judgment and Decision Making, 6(5):413--422.
[ bib ]
-
-
Pachur, T., Bröder, A., and Marewski, J. N. (2008).
The recognition heuristic in memory-based inference: is recognition a
non-compensatory cue?
Journal of Behavioral Decision Making, 21(2):183--210.
[ bib ]
-
-
Pachur, T. and Hertwig, R. (2006).
On the psychology of the recognition heuristic: Retrieval primacy as
a key determinant of its use.
Journal of Experimental Psychology: Learning, Memory, and
Cognition, 32(5):983--1002.
[ bib ]
-
-
Pachur, T., Mata, R., and Schooler, L. J. (2009).
Cognitive aging and the adaptive use of recognition in decision
making.
Psychology and Aging, 24(4):901.
[ bib ]
-
-
Pachur, T., Todd, P. M., Gigerenzer, G., Schooler, L. J., and Goldstein, D. G.
(2011).
The recognition heuristic: A review of theory and tests.
Frontiers in Psychology, 2(147):1--14.
[ bib ]
-
-
Pleskac, T. J. (2007).
A signal detection analysis of the recognition heuristic.
Psychonomic Bulletin & Review, 14(3):379--391.
[ bib ]
-
-
Pohl, R. F. (2006).
Empirical tests of the recognition heuristic.
Journal of Behavioral Decision Making, 19(3):251--271.
[ bib ]
-
-
Pohl, R. F. (2011).
On the use of recognition in inferential decision making: An overview
of the debate.
Judgment and Decision Making, 6(5):423.
[ bib ]
-
-
Pohl, R. F., Erdfelder, E., Michalkiewicz, M., Castela, M., and Hilbig, B. E.
(2016).
The limited use of the fluency heuristic: Converging evidence across
different procedures.
Memory & Cognition, 44(7):1114--1126.
[ bib ]
-
-
R Core Team (2015).
R: A Language and Environment for Statistical Computing.
R Foundation for Statistical Computing, Vienna, Austria.
[ bib |
http ]
-
-
Richter, T. and Späth, P. (2006).
Recognition is used as one cue among others in judgment and decision
making.
Journal of Experimental Psychology: Learning, Memory, and
Cognition, 32(1):150.
[ bib ]
-
-
Romney, A. K., Weller, S. C., and Batchelder, W. H. (1986).
Culture as consensus: A theory of culture and informant accuracy.
American Anthropologist, 88(2):313--338.
[ bib ]
-
-
Scheibehenne, B. and Bröder, A. (2007).
Can lay people be as accurate as experts in predicting the results of
wimbledon 2005.
International Journal of Forecasting, 23:415--426.
[ bib ]
-
-
Schooler, L. J. and Hertwig, R. (2005).
How forgetting aids heuristic inference.
Psychological Review, 112(3):610--628.
[ bib ]
-
-
Schwikert, S. R. and Curran, T. (2014a).
Familiarity and recollection in heuristic decision making.
Journal of Experimental Psychology: General, 143(6):2341--2365.
[ bib ]
-
-
Schwikert, S. R. and Curran, T. (2014b).
Familiarity and recollection in heuristic decision making.
Journal of Experimental Psychology: General, 143(6):2341--2365.
[ bib ]
-
-
Serwe, S. and Frings, C. (2006).
Who will win wimbledon? The recognition heuristic in predicting
sports events.
Journal of Behavioral Decision Making, 19(4):321--332.
[ bib ]
-
-
Simon, H. A. (1956).
Rational choice and the structure of the environment.
Psychological review, 63(2):129.
[ bib ]
-
-
Simon, H. A. (1990).
Invariants of human behavior.
Annual Review of Psychology, 41(1):1--20.
[ bib ]
-
-
Singmann, H. and Kellen, D. (2013).
MPTinR: Analysis of multinomial processing tree models in R.
Behavior Research Methods, 45(2):560--575.
[ bib ]
-
-
Smith, J. B. and Batchelder, W. H. (2010).
Beta-mpt: Multinomial processing tree models for addressing
individual differences.
Journal of Mathematical Psychology, 54(1):167--183.
[ bib ]
-
-
Snodgrass, J. G. and Corwin, J. (1988).
Pragmatics of measuring recognition memory: Applications to dementia
and amnesia.
Journal of Experimental Psychology: General, 117(1):34--50.
[ bib ]
-
-
Tomlinson, T., Marewski, J. N., and Dougherty, M. (2011).
Four challenges for cognitive research on the recognition heuristic
and a call for a research strategy shift.
Judgment and Decision Making, 6(1):89.
[ bib ]
-
-
Tversky, A. and Kahneman, D. (1974).
Judgment under uncertainty: Heuristics and biases.
science, 185(4157):1124--1131.
[ bib ]
-
-
Unkelbach, C. (2007).
Reversing the truth effect: Learning the interpretation of
processing fluency in judgments of truth.
Journal of Experimental Psychology: Learning, Memory, and
Cognition, 33(1):219 -- 230.
[ bib ]
-
-
Van De Schoot, R., Hoijtink, H., and Deković, M. (2010).
Testing inequality constrained hypotheses in sem models.
Structural Equation Modeling, 17(3):443--463.
[ bib ]
-
-
Zajonc, R. B. (1968).
Attitudinal effects of mere exposure.
Journal of Personality and Social Psychology, 9(2p2):1--27.
[ bib ]
This file was generated by
bibtex2html 1.98.
This document was translated from LATEX by
HEVEA.




