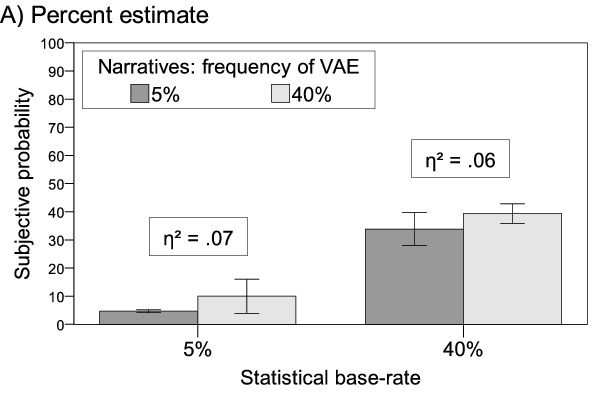
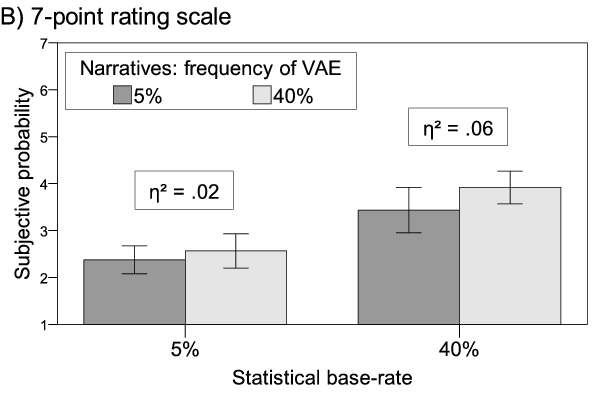
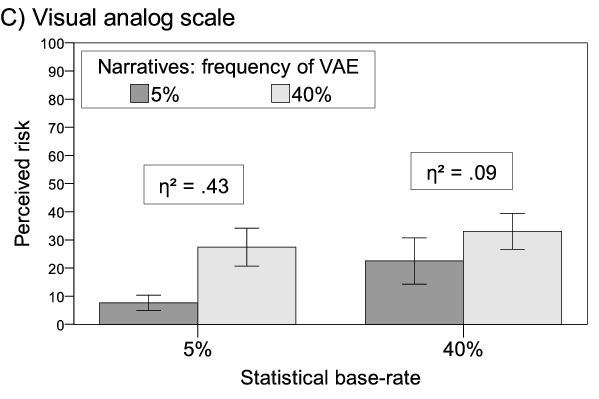
| Figure 1: Subjective probability (A: n = 89, B: n = 94) and perceived risk (C: n = 94) as a function of statistical and narrative information. All factors were manipulated between subjects. Error bars = 95% CI. |
Judgment and Decision Making, Vol. 10, No. 3, May 2015, pp. 241-264
The narrative bias revisited: What drives the biasing influence of narrative information on risk perceptions?Cornelia Betsch* # Niels Haase# $ Frank Renkewitz$ $ Philipp Schmid$ |
When people judge risk or the probability of a risky prospect, single case narratives can bias judgments when a statistical base-rate is also provided. In this work we investigate various methodological and procedural factors that may influence this narrative bias. We found that narratives had the strongest effect on a non-numerical risk measure, which was also the best predictor of behavioral intentions. In contrast, two scales for subjective probability reflected primarily statistical variations. We observed a negativity bias on the risk measure, such that the narratives increased rather than decreased risk perceptions, whereas the effect on probability judgments was symmetric. Additionally, we found no evidence that the narrative bias is solely produced by adherence to conversational norms. Finally, changing the absolute number of narratives reporting the focal event, while keeping their relative frequency constant, had no effect. Thus, individuals extract a representation of likelihood from a sample of single-case narratives, which drives the bias. These results show that the narrative bias is in part dependent on the measure used to assess it and underline the conceptual distinction between subjective probability and perceived risk.
Keywords: risk perception, subjective probability, narratives, cognitive bias, negativity bias.
Every day we encounter and act upon probabilistic information. From the weather forecast to consumer reports, individuals are regularly confronted with likelihood information about risks (e.g., the chance of rain) to inform their behavior in one way or another (e.g., whether to leave the house with or without an umbrella). In the medical domain, the advent of the modern shared decision making approach means that patients are increasingly involved in treatment and preventative decisions such as choosing between bypass surgery and angioplasty or deciding for or against vaccinations. All such decisions involve collecting, processing, and weighing probabilistic information. As a result, individual risk perception about medical matters has have been a recent focus of research.
At least 40 years of psychological research have produced an extensive catalog of situations in which likelihood estimates deviate from the prescriptions of probability theory (see Gilovich, Griffin, & Kahneman, 2002 for an overview). One such bias is the excessive influence of narrative information, exemplars, and testimonies, which we refer to as narrative bias. In a classic example, Borgida and Nisbett (1977) found that a few brief personal accounts had a far stronger impact on students’ course choices than mean course evaluations. Such reasoning is considered to be biased, i.e., formally incorrect, because it fails to weigh different samples of data according to the respective sample size.
One difficulty in understanding the mechanisms behind the narrative bias and in coherently summarizing findings lies in the different measures used to assess the influence of narrative information. Dependent variables vary from subjective probability to perceived risk or actual decisions (Betsch, Renkewitz, & Haase, 2013; Betsch, Ulshöfer, Renkewitz, & Betsch, 2011; Fagerlin, Wang, & Ubel, 2005; Obrecht, Chapman, & Gelman, 2009).
Researchers on biases in risk perception commonly collect some sort of magnitude judgment regarding the likelihood of a specified event (e.g., de Wit, Das, & Vet, 2008; Knapp, Gardner, Raynor, Woolf, & McMillan, 2010; Lee, Schwarz, Taubman, & Hou, 2010). However, even the most parsimonious, and also most common, definition of perceived risk (following expected value theory) additionally includes a value dimension, i.e., the significance or severity of a loss. Other concepts include the affective reaction to an outcome, the perceived source of a risk, the susceptibility to a risk, and degree of belief. Further, the voluntariness of risk, the knowledge about, and control over risk can also play a role in risk judgments (Brewer et al., 2007; Eiser, 1994; Gardoni & Murphy, 2013; Loewenstein, Weber, Hsee, & Welch, 2001; Slovic, Finucane, Peters, & MacGregor, 2004; Slovic, Fischhoff, & Lichtenstein, 1979; see Brun, 1994 for a comprehensive discussion of this topic). Thus, it seems prudent to distinguish between subjective probability and perceived risk.
In addition, although subjective probability and perceived risk are central variables in many studies, there is no consensus regarding their measurement. Methods include inferences from bets (Beach & Phillips, 1967), balls and bins tasks (Goldstein & Rothschild, 2014), risk matrices (Ball & Watt, 2013), and various self-report formats. The latter typically elicit a type of magnitude judgment and include numeric estimates, rating scales, and visual analog scales. One goal of this paper is to compare narrative biases across different measures used in previous research (Betsch et al., 2013, 2011; Obrecht et al., 2009).
Theoretical accounts of the highly persuasive effect of narrative evidence vary in focus and scope. Some explanations focus on the content of the narrative itself, which elicits affective reactions and immersion (see Hinyard & Kreuter, 2007 for an overview). Indeed, findings from previous research have shown that highly emotional narratives reporting vaccine adverse events increase the perceived risk of vaccination compared to less emotional narratives (Betsch et al., 2011). However, other findings show that the narrative bias occurs even when the content of the narrative is free of emotion and contains only the statement that the critical event occurred (Betsch et al., 2013; Obrecht et al., 2009). In this paper, we focus on a more formal approach that explains the narrative bias based solely on the structure of statistical and narrative information regardless of the narratives’ qualitative content.
Previous research that presented both statistical and narrative evidence to subjects has led to comparable results but differed regarding the causal explanation put forward by the authors. Ubel, Jepson, and Baron (2001) examined the importance of the match between statistical and narrative information and found that narratives were especially influential when the ratio of narratives indicating success vs. failure of a treatment was incongruent with previously presented statistical evidence. The effect, however, disappeared when controlling for the absolute number of narratives. Nevertheless, this finding indicates that individuals may perceive a set of narratives as a single unit of information—comparable to statistical information—that conveys the relative frequency of events.
Contrary to this idea, Obrecht et al. (2009) developed the encounter frequency theory, which assumes that each piece of information, be it a statistic or a single narrative case, is attributed equal weight when forming a judgment. Accordingly, individuals simply count each piece of information indicating the (non)occurrence of an event. Encounter frequency theory does not specify the process of how positive and negative counts are integrated. However, this account suggests that changing the absolute number of narratives reporting the occurrence of a focal event while keeping their relative proportion constant will affect judgments or decisions. A similar notion can be found in research on the ratio-bias or denominator neglect—i.e., the phenomenon that individuals tend to prefer a gamble with a 9/100 likelihood of winning over a gamble with a 1/10 likelihood, because they tend to ignore the denominator (Denes-Raj & Epstein, 1994; Reyna & Brainerd, 2008).
Thus, the second goal of this paper is to clarify whether the narrative bias relies on the relative or absolute number of narratives reporting the critical event.
There is some evidence that individuals tend to weigh information regarding the presence of a risk more strongly than information concerning its absence (Baumeister, Bratslavsky, Finkenauer, & Vohs, 2001; Rozin & Royzman, 2001; Siegrist & Cvetkovich, 2001). This negativity bias means that narratives may have an asymmetric effect. Narratives implying a higher risk than the provided statistical information would have a stronger influence on risk perceptions than narratives implying a lower risk than the statistical information. Therefore, a third goal is to test whether narratives can both increase and decrease risk perceptions, relative to the perception resulting from the statistical information alone.
We also strive to test the narrative bias against two potential and related alternative explanations that are inherent in the experimental procedure. First, it is possible that the narrative bias occurs simply because subjects follow conversational norms. That is, as experimenters we assume that the statistical information is the most or even only relevant information for the judgment. We expect individuals to attribute less weight to or even ignore the less reliable narrative information. However, Grice (1975) argues that conversation follows certain norms of cooperation, one of which states that communicated information is to be relevant. Thus, from the subjects’ point of view, all information provided by the experimenter may appear relevant for judgment due to the simple fact that it has been provided.
Second, in most studies comparing the influence of statistical and individuating information, statistical information is presented first followed by individuating information. Thus, it is possible that the narrative bias is at least partially caused by a recency effect. Expanding on the idea of conversational norms, Krosnick, Li, and Lehman (1990) argue that more informative and thus more important information is typically provided last, especially when two contradictory pieces of information are presented. Accordingly, subjects may assume that the experimenter considers the second piece of information, i.e., the narrative information, to be more important and that they should, in turn, do the same when making a judgment.
Finally, and related to this, we will investigate whether subjects would seek the narrative information at all if it were not provided. The act of seeking more information when sound statistical evidence is already available results in added costs to the individual—at least in terms of time. From a homo oeconomicus point of view, statistics provide the necessary likelihood information to quickly make a decision and should, therefore, be preferred over the time consuming evaluation of narrative reports.
Perceived risk and subjective probability are conceptually different; and there is no consensus on how to measure either one. Previous research has studied the narrative bias effect on both subjective probability, assessed either as percent estimates or by rating scales, and perceived risk measured using a visual analog scale. Experiment 1 asks whether the narrative bias is dependent on the task. Specifically:
RQ1: Do narratives and statistical information have different relative effects on a numeric and a verbal measure of subjective probability and a visual analog scale measure of perceived risk?
In previous studies, the relative frequency of the critical event as implied by the narratives typically exceeded that given by the statistical information, which led to an increase in perceived risk (Betsch et al., 2013, 2011). Research on the negativity bias (Siegrist & Cvetkovich, 2001) suggests that narratives may have an asymmetrical influence on risk perceptions such that they will have a greater impact when they exceed rather than fall below statistical risk information. Experiment 1 will therefore address the following research question:
RQ2: Is the narrative bias symmetric or asymmetric?
The same number of narratives indicating the occurrence of an event will lead to different risk perceptions if we assume that the relative rather than absolute frequency influences risk perceptions. Therefore, in Experiment 2, we strive to answer the question:
RQ3: Is the narrative bias caused by the relative or absolute number of narratives reporting the focal event?
Experiment 2 also explores questions related to the experimental procedure aimed to rule out the possibility that the narrative bias is an experimental artifact:
RQ4: Is the narrative bias partially an artifact produced by conversational norms in that the narratives have to be encoded and therefore appear to be relevant for judgments?
RQ5: Is the narrative bias partially caused by a recency effect when narratives appear after the statistical information?
RQ6: Is narrative information an attractive source of information when statistical information about a risk is already provided?
For the experiment content domain, we use vaccination risks. The example of vaccination risks seems particularly relevant in this context for two reasons: a growing number of individuals facing health related decision consult the Internet for information (Fox & Duggan, 2013); and narrative evidence is a common feature on anti-vaccination activist websites that propagate alleged adverse events and high risks of vaccination (Betsch et al., 2012; Haase & Betsch, 2012; Kata, 2010, 2012). In both experiments, subjects receive statistical and narrative information about the occurrence of vaccine-adverse events (VAE). They then judge the riskiness of the vaccination as well as the subjective probability of VAE.
In this experiment, we compared the effect of the narrative bias on three related measures. We asked for a percent estimate of the likelihood of VAE. Only numeric measures allow for a meaningful quantification of the narrative bias; and this format has been shown to be the least context dependent and less error-prone than judgments of relative frequency (Haase, Renkewitz, & Betsch, 2013; Weinstein & Diefenbach, 1997). As a second measure of subjective probability, we included a verbally labeled 7-point rating scale in order to retain comparability with previous studies (Betsch et al., 2011). Further, this 7-point rating scale has been shown to be superior in behavior prediction as compared to a percent measure (Weinstein et al., 2007). We will therefore explore whether we find comparable results regarding vaccination intentions. Finally, we assessed perceived risk by means of a visual analog scale. Since subjective probability and perceived risk are distinct constructs, we assessed all dependent variables for every subject and varied the order of assessment between subjects. In our analyses of the narrative bias, we examined only the first measure completed by each subject in order to exclude carry-over effects.
Because we differentiate between subjective probability and perceived risk, and definitions of risk typically include a value dimension, we additionally assessed the perceived severity of VAE. We also assessed the intention to get vaccinated in order to compare the different measures in terms of behavior prediction.
A total of 290 students at the University of Erfurt (24.5% male; MAGE = 22.16, SD = 3.159) participated in this lab-experiment in exchange for a small gift and the chance to win one of ten €50 notes (approx. US$67.50). Thirteen subjects were excluded because they had either taken part in a similar experiment before or reported in a post-experimental interview that they were unsure about the handling of the scales. Thus, the final sample includes N = 277 subjects, with n’s for individual analyses ranging from 22 to 27.
Each subject was randomly assigned to one of 12 conditions, resulting from a 2 × 2 × 3 between-subjects design with the relative number of narratives reporting VAE as the independent variable (1 or 8 narratives of 20, equaling 5% and 40%), the statistical probability of VAE (5% or 40%) as a second factor, and the first dependent variable as a third factor (7-point rating scale, percent estimate or visual analog scale). In addition, we assessed subjects’ numeracy, as previous work suggests that individuals with low numeracy may be especially prone to biases due to narrative information (Dieckmann, Slovic, & Peters, 2009; Peters, 2008).
All materials were presented on a computer screen. Subjects were provided with information about a fictitious severe disease (dysomeria) and the recommended vaccination. This was accompanied by a statistic reporting the likelihood of VAE occurring. Subsequently, subjects were asked to imagine that they found additional information about experiences with the vaccination on an Internet bulletin board. The narratives there reported either the occurrence (positive) or non-occurrence (negative) of VAE. Afterwards, subjects completed the dependent variable measures.
The statistical probability of VAE was explicitly expressed in percent together with a pictograph, i.e., a matrix of 100 elements colored in one of two ways which indicated the presence or absence of VAE (created with http://www.iconarray.com, last accessed on October 24, 2014). Pictographs have been shown to reduce the effect of narrative information (Fagerlin et al., 2005). We manipulated the statistical probability of VAE (5% vs. 40%) between conditions.
Table 1: Overview of dependent variables.
Construct Scale type Wording Subjective probability
Percent estimate What is the probability of experiencing adverse events if you get vaccinated? (You will experience adverse events with a probability of ___%.)
Subjective probability 7-point rating scale What is the probability of experiencing adverse events if you get vaccinated? (1 = almost zero, 2 = very small, 3 = small, 4 = moderate, 5 = large, 6 = very large, 7 = almost certain)
Perceived risk Visual analog scale How risky do you judge the vaccination to be? (0 = not risky at all, 100 = very risky)
Perceived severity
7-point rating scale How severe do you judge the possible adverse events of the vaccination to be? (1 = not severe; 7 = very severe)
Intention to get vaccinated
7-point rating scale If you had the possibility to get vaccinated in the next week, what would you do? (1 = I would definitely not get vaccinated, 7 = I would definitely get vaccinated)
Note. No numeric anchors were provided to the subjects. In Experiment 1 the materials were in German.
The narratives reported either the occurrence or non-occurrence of adverse events, with the number of narratives reporting VAE depending on condition (1 vs. 8 of 20 reports, resulting in 5% and 40%, respectively). The narratives were approximately equal in length (mean number of words = 57.5 and 52.2 for positive and negative narratives, respectively). In addition, positive narratives were pretested on 9-point rating scales concerning the severity of reported VAE, emotionality of content, and credibility. We selected narratives with moderate severity and emotionality, i.e., ratings did not differ from a midpoint rating of 5 (severity: all t’s ≤ 1.66, emotionality: all t’s ≤ 1.98). The narratives were rated as equally credible (mean ratings did not differ from a rating of 6, all t’s ≤ 1.48). The fictional authors’ first names for all narratives were balanced for gender. The narratives were displayed as single cases, with one narrative per page. The pages were displayed in random order. In order to minimize any systematic influence due to additional information in the text, e.g., concerning the vaccination procedure, narratives were elected at random when the whole sample was not needed. For example, in the 5% condition, one positive narrative out of a total of eight positive narratives (that were used in the 40% condition) was drawn for each subject. Appendix A presents four example narratives.
Table 1 provides an overview of all dependent variables. Subjects completed all measures; however, the order of the following measures was varied between subjects: the subjective probability of the occurrence of adverse events (measured via two measures: numeric estimate in percent and probability rating on a 7-point rating scale) and the perceived risk of the vaccination (visual analog scale). For perceived risk, we used a non-numeric format so as to avoid making the probability dimension especially salient. However, to allow for comparisons with the subjective probability judgments and a quantification of the narrative bias, the visual analog scale provided scores between 0 and 100. No numeric feedback was provided to subjects.
In the subjective probability conditions, subjects provided their ratings on the specific subjective probability measure followed by the respective other measure and the visual analog scale to assess perceived risk. In the perceived risk condition, risk was assessed on the visual analog scale followed by the subjective probability measures in counterbalanced order. After all three measures were completed; we assessed the severity of the possible adverse events as well as subjects’ intentions to get vaccinated.
After completing the dependent measures, subjects were asked to reproduce the stated statistical probability (5% or 40% depending on condition) and report the number of cases that reported VAE on the bulletin board (1 or 8).
Subjective numeracy was assessed with a German translation of the Subjective Numeracy Scale (Fagerlin et al., 2007; German translation by Keller, Siegrist, & Visschers, 2009). The eight items were answered on a 6-point scale, where higher ratings indicate greater subjective numeracy (e.g., How good are you at working with fractions?).
Table 2: Subjective probability (percent estimate, 7-point rating scale) and perceived risk as a function of the statistical base-rate, relative frequency of narratives reporting VAE, and subjective numeracy (Experiment 1).
Subjective probability (percent estimate) n = 89 .81 <.001 .83 <.001 .15 .02 .14 .03 .00 .97 -.02 .79 -.01 .84 .10 .12 -.14 .02 -.03 .58 .68 .71 Subjective probability (7-point rating scale) n = 94 .56 <.001 .55 <.001 .16 .07 .17 .06 .07 .43 .03 .71 .03 .75 .22 .02 .09 .30 .07 .42 .35 .39 Perceived risk (visual analog scale) n = 94 .29 .002 .29 .002 .43 <.001 .42 <.001 -.13 .14 -.14 .14 .01 .93 .02 .85 -.03 .74 -.06 .51 .29 .30 Note. Standardized betas (β) and respective p-values of significant effects are shown in boldface.
In both conditions, roughly 96% of subjects were able to reproduce the given statistical probability (5% or 40%). We assumed a correct recall of the number of narratives if the recalled number was plus/minus one. For the condition in which 1 narrative reported VAE, 94.9% correctly recalled the absolute number (M1 = 1.4, SD1 = 1.75). In the 8 cases condition, 51% (M8 = 8.33, SD8 = 2.29) correctly recalled the absolute frequency of narratives reporting VAE. As the results did not change after eliminating subjects who did not correctly recall the encoded information, we used the full sample in our analyses.
The obtained internal consistency of all items was sufficient, α = .77. The mean score of answers constitutes the subjective numeracy score (potential range 1–6). The mean subjective numeracy score (4.21, SD = 0.76) did not differ across conditions (all η2p’s in a 2 × 2 × 3 ANOVA were ≤ .01, all p’s ≥ .09).
Figure 1: Subjective probability (A: n = 89, B: n = 94) and perceived risk (C: n = 94) as a function of statistical and narrative information. All factors were manipulated between subjects. Error bars = 95% CI. 


The first goal of this experiment was to compare the effects of statistical and narrative information on different measures of perceived risk and subjective probability. Therefore, we calculated regression analyses for the measures using only the subsamples that responded to the respective construct first in the order of dependent variables. We excluded the samples in which other measures were completed prior to the dependent variable of interest to exclude carry-over effects (e.g., the influence of the numerically recalled probability on the general judgment of risk). Thus, we calculated three linear regressions predicting subjective probability (percent estimate and rating scale) and risk (visual analog scale), respectively. For all analyses we used standardized, continuous predictors. Interactions were calculated as the mathematical products of the factors (Cohen, Cohen, West, & Aiken, 2003). In a first regression, we entered the manipulated factors and their interaction. In a second regression, we added subjective numeracy and the interactions of the factors with subjective numeracy.1
The main results of the separate regressions are displayed in Table 2. The narrative biases are displayed in Figure 1. Both the statistical base-rate (β = .81) and the narratives (β = .15) significantly influenced the subjective probability of experiencing adverse events assessed as percent estimate. The statistical information had a stronger influence than the narrative information. A similar pattern of effects occurred when subjective probability was assessed by means of a 7-point rating scale (statistical base-rate: β = .56, narratives: β = .16), although the narratives’ influence was not significant. For perceived risk assessed with the visual analog scale, however, the influence of the statistical base-rate information was lower than that of the narratives (statistical base-rate: β = .29, narratives: β = .43), indicating a stronger narrative bias.
In order to assess the different effects of narratives and statistics on the three dependent measures we also correlated each of the three dependent measures with the difference between the statistical and narrative information. This was done only for those subjects for whom narrative information differed from the statistical base-rate. Differences were calculated by subtracting the frequency of VAE from the statistical base-rate, so a difference of -35% represents a low base-rate and a higher probability in the narratives, a difference of 35% represents the opposite. This way, a negative correlation indicates a stronger effect of narratives, a positive one a stronger effect of the statistical information. The correlations were r = .67, p < .001 for the percent estimate (n = 44), r = .41, p = .005 for the 7-point rating scale (n = 46), and r = -.15, p = .34 for the visual analog scale (n = 45). The last of these differed significantly from the other two (Percent estimate: Fisher’s z = 4.38, p < .001, 7-point rating scale: Fisher’s z = 2.7, p = .007).
When we entered subjective numeracy into the regression model, the percent estimate was a function of the number of narratives only when subjects had low subjective numeracy scores. Subjects high in subjective numeracy were unaffected by the number of narratives when judging the probability of VAE. This is evident in a significant interaction between subjective numeracy and the relative number of narratives (β = -.14).
When subjects judged the probability of VAE on the 7-point rating scale, the resulting judgments differed more strongly between the 5% and 40% statistical conditions for subjects high in subjective numeracy. Judgments by subjects low in subjective numeracy were more similar across statistical conditions. This was indicated by a significant interaction of subjective numeracy and statistical probability of VAE (β = .22).
Subjective numeracy did not affect ratings on the risk measure (visual analog scale; all β’s n.s.).
Figure 2: Perceived risk (n = 183) as a function of the statistical and narrative information. Subjective probability was assessed before the risk judgment. All factors were manipulated between subjects. Error bars = 95% CI. 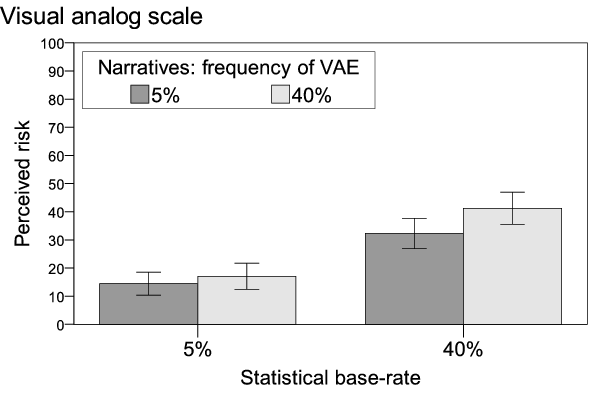
The results above suggest that risk judgments and subjective probability judgments are indeed very different—the probability judgments were less biased by narrative information than the risk judgment and depended more on the statistical base-rate. Judging probabilities before judging risk, therefore, may increase the saliency of the probability dimension of risk, resulting in a larger effect of the statistical base-rate on risk judgments. Conversely, judging risk before probability might increase the influence of narrative information. Both kinds of influence should manifest themselves in carry-over effects. To test this, we calculated three additional regression analyses with the respective other subsample, i.e., we predicted ratings on the probability scales using only subjects that had first judged perceived risk and, vice versa, predicted risk judgments of subjects who had first estimated subjective probability of VAE.
Percent estimates were not affected by a prior risk judgment (Statistic: β = .81, p < .001, Narratives: β = .19, p = .002). Subjective numeracy had no influence (all other T’s ≤ 1.45; R2 = .72, F(7,86) = 31.62, p < .001).
For the 7-point rating scale, on the other hand, we found a similar significant influence of statistical variation (β = .56, p < .001) but also a significant effect of the narratives (β = .25, p = .003). Again, there was no effect of subjective numeracy (all other T’s ≤ 1.48; R2 = .41, F(7,86) = 8.36, p < .001). This indicates that considering the whole risk construct first renders a probability judgment more susceptible to the influence of irrelevant information.
For the risk measure, we found that judging probability first reversed the relative influence of both information types, thus resulting in a stronger influence of statistical information (β = .51, p < .001) than of the narratives (β = .16, p = .012; all other T’s ≤ 1.21; R2 = .32, F(7,175) = 11.86, p < .001) on subsequent risk judgments. Note that increasing the salience of the probability dimension not only increased the effect of statistical information but also decreased the narratives’ influence (see Figure 2 compared to Figure 1C).
In order to assess whether the narrative bias is symmetric, we compared the effect sizes of the conditions when narratives were expected to increase vs. decrease the resulting judgments. The bars on the left in Figure 1 represent the case in which narratives should increase ratings of subjective probability and risk, because the relative frequency of narratives reporting VAE is equal to or greater than the statistical base-rate of 5%. The bars on the right represent the case in which narratives report an equal to or lower probability of VAE than the statistical information. If the narrative bias is symmetric, effect sizes displayed in Figure 1 should not differ between an expected increase vs. decrease (left vs. right).
In the case of the percent estimates, we observed a symmetric narrative bias in both directions. For the 7-point rating scale, the decreasing effect was slightly larger than the increasing effect, although both effects were rather small. For the risk measure, we observed a strong negativity bias, indicating that narratives increased rather than decreased risk perceptions.
For each subsample, separate correlation analyses between the intention to get vaccinated and the respective dependent variable revealed virtually identical coefficients (rPERC = -.31, r7-POINT = -.33, rRISK = -.31, all p’s < .01). However, in an additional step-wise regression analysis across all subjects (N = 277) only perceived risk predicted the intention, whereas both other variables were excluded from the analysis (βRISK = -.43, p < .001; R2 = .19).
These results might indicate multicollinearity, i.e., even though each measure predicts the intention on its own, they actually account for the same variance because they are correlated. In line with this, the correlation coefficients in Table 3 indicate that the percent estimate and the 7-point rating scale have some predictive power but that perceived risk accounts for the same as well as for additional and unique variance in vaccination intentions. Appendix C presents the same correlation matrices as Table 3 for each subsample. The absolute predictive power of all measures varies but the relation between measures remains stable, with perceived risk as the best predictor of behavioral intentions.
Table 3: Correlations between subjective probability (percent estimate, 7-point rating scale), perceived risk, and intention to get vaccinated for the full sample in Experiment 1 (N = 277).
— .70*** — .61*** .74*** — -.22*** -.34*** -.43*** — *p < .05. **p < .01. ***p < .001.
Narratives biased the perception of subjective probability and risk to different extents, depending on the measure with which the dependent variables were assessed. The relative effect of narratives was largest (and even a little larger than the effect of the statistical information) on perceived risk assessed with a visual analog scale. The narratives had a similar but smaller to negligible effect on both measures of subjective probability (RQ1). Variations in statistical information, on the other hand, had the greatest effect on subjective probability assessed as a percent estimate and the smallest effect on perceived risk assessed with a visual analog scale. These results underline the important conceptual distinction between subjective probability and perceived risk. Risk perception is often operationalized as a likelihood judgment. However, the manipulation of probabilistic information (all other variables were held constant) affected judgments of subjective probability and perceived risk differently. This is especially apparent when considering RQ2. The narrative bias was symmetric only when subjective probability was assessed in percent—i.e., when narratives suggested a lower likelihood than the statistical base-rate, subjective probability decreased; it increased to the same extent when narratives suggested a higher likelihood compared to the statistical base-rate. Contrary to this finding, we observed a strong negativity bias on the risk measure—i.e., a greater increase than decrease in risk perceptions due to narratives.
Previous research indicates that the 7-point rating scale is less sensitive to variations in objective probabilities (Betsch et al., 2011; Haase et al., 2013), which is supported by the present results: The 7-point rating scale was less able to map differences in the statistical base-rates than the percent estimates. In addition, the effect of narratives was smallest on this scale. If quantifying the effect of narratives on subjective probability is a goal, subjective probability should be assessed as percent estimates. Experiment 2 will therefore omit the 7-point rating scale.
In additional analyses, we found that individual differences in subjective numeracy play a differential role concerning the judgment of subjective probability both as a percent estimate and on a rating scale. Low subjective numeracy increased the influence of narratives when providing percent estimates, which matches previous findings (Dieckmann et al., 2009). For the 7-point rating scale, low subjective numeracy was related to less differentiation between statistical base-rates. Highly numerate subjects used the 7-point rating scale more broadly to differentiate between the 5% and 40% base-rate. In line with this, Peters and Bjalkebring (2014) found higher subjective numeracy to be related to better performance in a symbolic-number mapping task.
Experiment 1 implicitly assumes that the relative frequency of narratives reporting the critical event influences risk perceptions. However, as stated in the introduction, encounter frequency theory and research on the ratio-bias suggest that the absolute number of narratives may drive this effect. In the current experimental paradigm, individuals would then perceive different risks when 8 of 20 narratives report VAE than when 4 of 10 do so. Thus, in this experiment we vary the absolute number of narratives while keeping the relative number of positive cases constant (RQ3).
In order to investigate whether the narrative bias is in part an experimental artifact, additional experimental conditions offer subjects the option to decide whether they want to view the narrative information in addition to the statistical information. This should communicate to subjects that the statistical information is sufficient to make a judgment (RQ4) and will also allow us to address the question whether narratives are an attractive source of information that are sought out even when statistical information is already available (RQ6). Further, in certain conditions we vary the sequence of statistical and narrative information to exclude recency as an alternative explanation (RQ5).
The experimental set-up strongly resembled the first experiment.
Subjects were recruited via Amazon Mechanical Turk and were paid US$1 (hourly wage: approx. US$4.14) through the Mechanical Turk payment system. Of the 515 individuals who clicked on the link to the survey, 479 completed the study. We excluded one individual who copied text from the page into a textbox, indicating that he or she did not read the instructions. In addition, we excluded three subjects who completed the survey in less than 5 minutes (M = 13 min 56 s, SD = 6 min), which falls below the minimum completion-time. Finally, 11 subjects indicated that they had previously participated in a similar study and were therefore excluded from the sample. Thus, analyses were calculated with a sample of N = 464 subjects, with the n for individual conditions ranging from 24 to 31.
Figure 3: Design of Experiment 2. Top of the figure shows the main 2 × 2 × 3 design, the bottom shows both subdesigns. Dashed borders indicate cells from the main design used for comparison with the subdesigns. 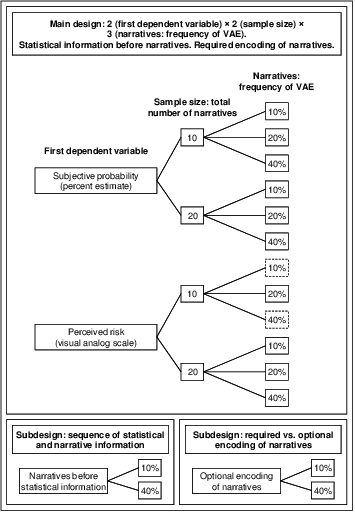
Subjects were randomly assigned to 16 conditions, resulting from a 2 × 2 × 3 between-subjects design plus four additional conditions described below (see Figure 3). The main design is constituted by the following factors: 2 (sequence of dependent variables: risk perception followed by subjective probability and vice versa) × 2 (sample size: 10 vs. 20 cases) × 3 (relative frequency of narratives reporting adverse events: 10% vs. 20% vs. 40%). The statistical base-rate information was equal in all conditions (20%). Additionally, we assessed subjects’ numeracy.
In order to test whether the narrative bias occurs due to a conversational norm indicating that all information provided must be relevant, we added two cells in which reading the narratives was optional, in contrast to all the above mentioned conditions in which reading the narratives was required. We did so in a 2 × 2 between-subjects subdesign, using two cells from the design reported above: 2 (relative frequency of adverse events: 10% vs. 40%) × 2 (encoding of narrative information: required vs. optional). If an interaction suggests that the narrative bias disappears when encoding of the narratives is optional rather than required, we can assume that at least part of the narrative bias occurs due to the subjects’ tendency to view all materials presented by the experimenter as relevant. For economic reasons, we decided to use only the risk measure as a dependent variable.
In order to test whether the narrative bias occurs due to a recency effect, we added two additional conditions in which we varied the order of the statistical and narrative information. Thus, the resulting 2 × 2 between-subjects subdesign was constituted by the following factors: 2 (relative frequency of adverse events: 10% vs. 40%) × 2 (sequence of information: statistic–narratives and vice versa). If an interaction suggests that the narrative bias disappears when the statistical information is presented after the narratives and before the dependent variables, we can assume that at least part of the narrative bias occurs due to a recency effect. Again, we used only the risk measure.
As in Experiment 1, subjects read about the disease, the vaccine recommendation, and the statistical likelihood of VAE in written and graphic form. They were then presented with the narrative information within a simulated bulletin board. Finally, we collected dependent variables, manipulation checks, and control variables.
As in the first experiment, the statistical probability of VAE was stated explicitly in percent and displayed by means of a pictograph and was fixed at 20% in all conditions. The narratives either matched, exceeded, or fell below the statistical information.
In all conditions, either 1, 2 or 4 of 10 or 2, 4 or 8 of 20 narratives reported VAE (resulting in relative frequencies of 10%, 20% and 40%, respectively). All reported adverse events were categorized as mild (e.g., insomnia, fever, rash; as identified in a pretest, see Experiment 1). The remaining cases reported unproblematic vaccination experiences. As in Experiment 1, the narratives were of equal length, randomized in their sequence, and displayed one at a time.
Two conditions offered subjects the choice to either view the narrative information or skip the simulated bulletin board. Subjects were asked: "Next, you have the opportunity to read a number of posts from an online message-board where people share their personal experiences with the vaccine. Would you like to read the posts?" (yes or no). In all other conditions, subjects were informed that on the subsequent pages they will see "a number of posts from an online message-board where people share their personal experiences with the vaccine". The instructions asked them to read all messages carefully.
All subjects learned that their doctor provided them with the statistical information. In two conditions, the statistical information appeared after the narrative information. In all other conditions, the statistical base-rate information was provided first.
As dependent variables, we assessed perceived risk and subjective probability in the same manner as in Experiment 1 (Table 1). As a measure for subjective probability, we asked for percent estimates. Half of the subjects judged the subjective probability of VAE first and then rated their perceived risk and vice versa for the other half.
We asked subjects to recall the initially stated base-rate of VAE (20%) as well as the number of narratives that reported adverse events (1, 2, or 4 of 10 or 2, 4, or 8 of 20). We asked for the number of narratives only if the subjects had either seen them by default or if they had decided to read them.
In this experiment, we employed a more objective measure of numeracy—a combination of the 3-item scale by Schwartz, Woloshin, Black, and Welch (1997) and the Berlin Numeracy Test (Cokely, Galesic, Schulz, Ghazal, & Garcia-Retamero, 2012). The seven items involve short mathematical quizzes (e.g., "Imagine we are throwing a five-sided die 50 times. On average, out of these 50 throws, how many times would this five-sided die show an odd number (1, 3 or 5)?", correct answer = 30).
Table 4: Subjective probability and perceived risk as a function of sample size, frequency of VAE, and numeracy (Experiment 2).
Subjective probability (percent estimate) n = 181 -.04 .61 -.03 .70 .10 .16 .09 .26 -.14 .06 -.13 .09 -.02 .80 .05 .50 -.10 .19 .11 .15 .03 .06 Perceived risk (visual analog scale) n = 168 -.07 .36 -.07 .35 .38 <.001 .37 <.001 .04 .60 .04 .62 -.14 .05 .02 .76 -.14 .05 .13 .06 .15 .20 Note. Standardized betas (β) and respective p-values of significant effects are shown in boldface.
Ninety-two percent of subjects correctly recalled that the statistical base-rate was 20% (M20 = 21.16, SD20 = 9.12); 4% reported that it was below 20%, whereas 4% reported a base-rate greater than 20%.
We assumed a correct recall of the number of narratives if the recalled number was plus/minus one. For the condition in which 1 narrative reported VAE, 95.3% correctly recalled the absolute number (M1 = 1.30, SD1 = 1.32). In the 2 cases condition, 93.2% (M2 = 2.45, SD2 = 1.77), in the 4 cases condition 85.1% (M4 = 4.71, SD4 = 4.12), and in the 8 cases condition 41.4% (M8 = 8.97, SD8 = 11.78) correctly recalled the absolute frequency of narratives reporting VAE.
The sum score of all correctly solved numeracy items constitutes the numeracy score (potential range 0–7). The mean numeracy score (3.50, SD = 1.79) did not differ across conditions (all η2p’s in a 3 × 2 × 2 ANOVA were ≤ .003, all p’s ≥ .32).
The goal of this experiment was to assess whether the narrative bias occurs due to the relative or absolute frequency of narratives reporting VAE (RQ3). A main effect showing an increase with sample size (number of messages on the bulletin board) would indicate that the absolute number of narratives reporting VAE (possibly as well as the relative number) influences the dependent variables, because the absolute number of narratives is higher in the 20 cases condition (2, 4, 8) than in the 10 cases condition (1, 2, 4).
For all analyses, we calculated regression analyses with standardized, continuous predictors. Two separate linear regressions were calculated, predicting subjective probability (percent estimates) and perceived risk (visual analog scale). We again used only the subsamples in which the respective dependent variable was assessed first to exclude carry-over effects. Interactions were calculated as the mathematical products of the standardized predictors (Cohen et al., 2003). In a first regression, we entered the manipulated factors and their interaction. In a second regression, we added numeracy and the interactions of the factors with numeracy.2
Table 4 displays the results of the regression analyses. Subjective probability tended to be influenced by the relative frequency of positive narratives when the sample was small (10 cases) and was not influenced when it was large (20 cases), as indicated by an almost significant interaction of narratives and sample size (β = -.14). The effect was somewhat weaker when numeracy and the respective interactions were also entered into the regression. No other effects were significant.
Figure 4: Unstandardized simple slopes of frequency of VAE predicting perceived risk for the small and the large sample. 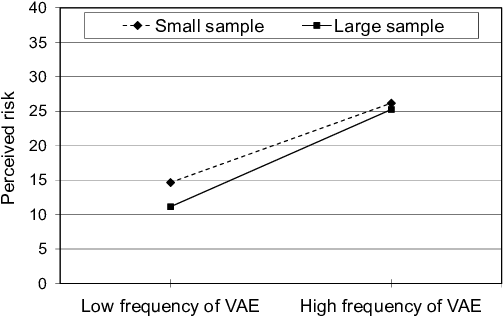
Figure 5: Unstandardized simple slopes of frequency of VAE predicting perceived risk for 1 SD below and 1 SD above the mean of numeracy. 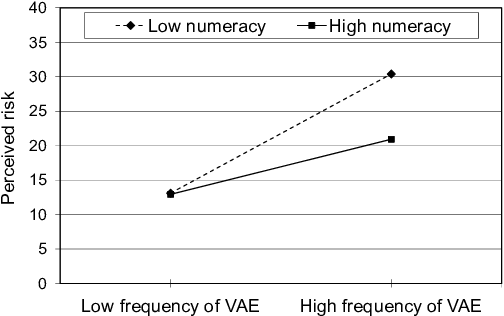
Figure 6: Unstandardized simple slopes of frequency of VAE predicting perceived risk for 1 SD below and 1 SD above the mean of numeracy, separate for the small and the large sample, illustrating the three-way interaction. 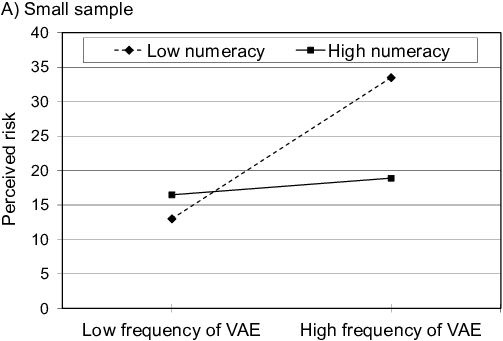
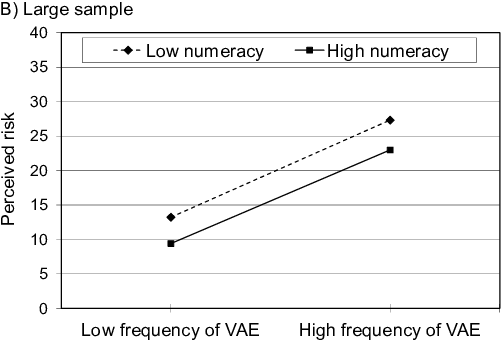
Perceived risk was a function of the relative frequency of narratives reporting VAE (β = .38), with subjects in conditions with a higher relative frequency perceiving higher vaccination risks. The sample size did not affect perceived risk (Figure 4).3
Subjects with high numeracy generally perceived lower risk (β = -.14). Two interaction effects qualified this main effect. For highly numerate subjects, there was a weaker narrative bias, whereas the bias was stronger for subjects with low numeracy (Figure 5). The almost significant three-way interaction is displayed in Figures 6A and 6B, which show that there was no narrative bias for highly numerate subjects when the sample size was small.
In order to rule out the possibility that the lack of an effect of sample size was due to subjects not encoding the larger number of narratives as carefully as the small number, we analyzed reading times. We conducted two separate 2 × 2 × 3 ANOVAs with the total amount of time spent reading the narratives and the average amount of time per narrative as respective dependent variables. Subjects took almost exactly twice as long to encode 20 narratives (M20 = 3 min 31 s, SD = 2 min 5 s) as compared to 10 narratives (M10 = 1 min 46 s, SD = 57 s; F(1,337) = 60.96, p < .001, η2p = .15). There were no other significant effects (F’s ≤ 1.11). Correspondingly, average reading times per narrative were virtually identical in the small and large sample conditions (M10 = 11 s, SD = 6 s; M20 = 11 s, SD = 8 s) and did not differ across any conditions (F’s < 1). Additionally, adding either time variable had no effect on the regression models.
Thus, the results show that subjects encoded small and large samples equally well. As there was no main effect of sample size on either dependent variable, this indicates that subjects extracted a relative frequency representation from the narratives. This relative frequency, rather than the absolute number of cases, drives the narrative bias (RQ3).
Again, to test for carry-over effects, we calculated the same two regression models for the respective other subsample. Considering the whole risk construct first led to a significant narrative bias on subjective probability estimates (β = .26, p = .001). An almost significant interaction with numeracy indicated that this bias was more pronounced for low numerate individuals (β = -.14, p = .06; all other T’s < 1; R2 = .10, F(7,160) = 2.48, p = .019).
A prior probability estimate, on the other hand, decreased the influence of narrative variation on the risk judgment (β = .20, p = .009) and rendered all further effects non-significant (all other T’s ≤ 1.81; R2 = .09, F(7,173) = 2.34, p = .026).
Of the subjects who had a choice to read the narratives, 78.2% (n = 43) decided to do so. We conducted a 2 (frequency of VAE: 10% vs. 40%) × 2 (encoding of narrative information: required vs. optional) ANOVA with perceived risk as dependent variable. The analysis revealed only a strong narrative bias (F(1,92) = 19.11, p < .001, η2p = .17, all other F’s < 1). Consequently, we assume that narrative information affects risk perceptions irrespective of whether it had to be read or was freely chosen (RQ4).
In order to test for recency effects, we conducted a 2 (frequency of VAE: 10% vs. 40%) × 2 (sequence of statistical and narrative information) ANOVA with perceived risk as the dependent variable. We found a strong main effect for the relative frequency of VAE (F(1,109) = 16.07, p < .001, η2p = .13). All other effects were nonsignificant (F’s ≤ 1.7). Thus, the narrative bias occurred regardless of whether statistical base-rate information was provided before or after the narratives were encoded. This indicates that the narrative bias is not caused by a recency effect (RQ5).
For all subjects (N = 464) the correlation between perceived risk and intention to get vaccinated is r = -.41 (p < .001). Subjective probability and intention are not correlated (r = .01, n.s.). Because we observed muticollinearity in Experiment 1, Appendix C presents correlations between both measures and intention. When perceived risk was assessed first, it correlates with subjective probability. However, in both subsamples only perceived risk predicts behavioral intentions.
In two experiments we found that the biasing influence of narrative information on risk perception is in part a function of the dependent measure used to assess it. Narratives had the largest effect on a non-numerical risk measure, whereas two scales for subjective probability reflected mostly statistical variations. This stresses the importance of differentiating between the constructs risk and probability. Further, two-way carry-over effects between the respective measures indicated that the use of all scales was context dependent, e.g., considering the risk construct first increased the influence of narrative information on subsequent probability judgments. Additionally, the risk measure was the best predictor of behavioral intentions, and only for the risk measure did we observe a negativity bias. Moreover, results indicate that subjects extracted a representation of relative frequency from the narratives, as changing the absolute number of single events while keeping their relative number constant did not change the narrative bias. Subjective and objective numeracy had opposing and somewhat weak effects on judgments. Finally, the option to freely choose whether to read the narrative information did not affect the narrative bias in any way. In addition, we found no indication of a recency effect as an explanation for the narratives’ influence.
Regarding the task dependence of the narrative bias, three aspects of measuring risk perception must be considered: the representation on which a judgment is based, the scale used for assessment, and the context in which the scale is used.
Various theoretical approaches propose that risk judgments rely on two distinct representations or processes. These theories make diverse yet conceptually related differentiations between cognitive vs. affective risk evaluations, a belief in objective probabilities vs. an intuitive perception of risk, and verbatim vs. gist representations. The two respective components are understood to be distinct but may interact in the reasoning process, which moves along a continuum between them (Loewenstein et al., 2001; Reyna, 2008, 2012; Slovic et al., 2004; van Gelder, de Vries, & van der Pligt, 2009; Windschitl, Martin, & Flugstad, 2002).
The scales we used differ along at least two dimensions. First, whereas the rating scale offers only seven discrete categories for judgment, the percent format and the visual analog risk scale allow for quasi-continuous estimates, i.e., 101 discrete categories, as responses were restricted to integers. This difference in resolution provides the latter scales with a natural advantage in terms of sensitivity to changes in subjective probability (Haase et al., 2013). Second, while the percent format is purely numeric, the rating scale and risk measure provide verbal labels. It has been argued that numeric probability measures induce rule-based reasoning in individuals and elicit beliefs in objective probability, whereas verbal scales lead to a more associative reasoning style and elicit rather intuitive thoughts about an uncertain prospect. These intuitive beliefs entail more than just a maximally accurate representation of likelihood. Rather, they also include notions of the value of a prospect, affective reactions to it, and its meaning in a given situation—all of which may make them more comparable to real-life situations. Accordingly, verbal probability scales have been shown to be more sensitive to context and framing effects as well as to be better predictors of preferences, behavioral intentions, and behavior than numeric scales. The risk measure extends this idea on an explicit conceptual level, as risk by definition encompasses more than mere probability. In addition, risk measures have been found to perform even better in predicting behavior (Baghal, 2011; Weinstein et al., 2007; Windschitl, 2002; Windschitl & Wells, 1996).
Finally, the interpretation of a question and the use of a response format have been shown to be affected by the context such as a preceding question (Schwarz, 1999, 2007). Building on these premises, we suggest that judgments in research on biased risk perception are in part task-dependent (RQ1). Subjects base their estimates on beliefs in objective likelihood and intuitive risk representations and engage in rule-based and associative reasoning styles. The degree to which these two representations inform the judgment and the manner in which they are weighed and processed are in part a function of the response scale provided, as well as prior elicitations of related constructs.
In line with this notion, narrative and statistical information affected the three dependent variables differently. Judgments on the 7-point rating scale were not influenced by variations in the narrative information (Experiment 1), which can partly be explained by the scale’s low sensitivity, as even the explicitly stated statistical probabilities of 5% and 40% were mapped very close to each other on the rating scale. However, the verbal qualifiers of this scale make judgments prone to reflecting not only a likelihood representation but also other aspects of the uncertain prospect, e.g., the severity of VAE (Weber & Hilton, 1990), which may have masked the effect of the narrative manipulation. Indeed, controlling for perceived severity (β = .19, p = .02) in the regression model not only significantly increased the amount of explained variance (from R2 = .39 to R2 = .43, F(1,85) = 5.31, p = .02) but also rendered the variation in narratives a significant predictor of subjective probability (β = .17, p = .05, all other effects unchanged). We assume that these subjects attempted to provide judgments which, for the most part, reflect their beliefs in objective probability, as this was the first question asked. In contrast to this, estimates by subjects who had first considered the whole risk construct showed a clear narrative bias, indicating that subjects’ interpretation of the 7-point rating scale—as a pure probability measure vs. a general risk measure—varies as a function of contextual factors.
The percent format, in comparison, elicits responses that are almost exclusively expressions of rule-based reasoning processes concerning numeric probabilities. The effect of variations in narrative information was smaller (Experiment 1) or negligible (Experiment 2) and symmetric as compared to the effect on risk judgments. Further, adding severity to the regression model had no effect in either of the experiments. Subjects encoded the likelihood of VAE in percent and were later asked for an estimate in percent. Thus, the format might have cued the retrieval of this specific information rather than a subjective representation of probability. However, even the percent format is not fully resistant to context effects—in Experiment 2, asking for a general risk judgment beforehand led to a narrative bias.
Finally, we observed the strongest narrative bias on the visual analog risk scale. In Experiment 1, narratives had a stronger effect on risk perceptions than the statistic. In Experiment 2, only risk perceptions were affected by narrative information. Further, perceived severity proved a strong predictor of perceived risk and improved the model to a large degree in both experiments (Experiment 1: β = .31, p = .001; from R2 = .30 to R2 = .39, F(1,85) = 12.17, p = .001; Experiment 2: β = .48, p < .001; from R2 = .20 to R2 = .42, F(1,159) = 61.36, p < .001; all other effects unchanged). As individuals expressed more than just a likelihood representation in their risk judgments, these estimates might be especially susceptible to contextual factors. Accordingly, asking for a probability estimate first increased the influence of statistical information on perceived risk (Experiment 1) and decreased the effect of narrative variation (both experiments). Still, risk estimates did not represent merely an analytic integration of likelihood and value. Additionally controlling for subjective probability estimates in the regression models eliminated the effect of statistical variation (Experiment 1) but not the effect of narratives on risk judgments (both experiments).
In line with previous research and our reasoning thus far, we found that the risk measure predicted behavioral intentions best. Decisions and behavior under risk, of course, have more antecedents than just the likelihood of a given outcome. Thus, a measure that elicits more than this likelihood representation will consequently lead to superior predictions. Our findings regarding the symmetry of the narrative bias (RQ2) lend further support to this explanation. When asked to provide percent estimates, subjects engaged in rule-based integration akin to a calculation, which, since the presented frequencies were symmetric, resulted in a symmetric bias. A more intuitive risk measure, on the other hand, led to a clear negativity bias. One explanation for the stronger impact of negative information is that it possesses greater diagnostic value. Consider the potential cost of ignoring a danger versus mistakenly missing out on a benefit. If judgments of perceived risk are more relevant for actual behavior, it would make sense to assign negative information more weight. However, when the judgment process follows a normative understanding of mathematics, equal numbers will receive equal weights (Baumeister et al., 2001; Siegrist & Cvetkovich, 2001; Skowronski & Carlston, 1989).
The narrative information provided subjects with exemplars of the occurrence and non-occurrence of an uncertain outcome, i.e., VAE. The encoding of such event frequencies is a predominantly automatic and accurate process (Hasher & Zacks, 1979; Zacks & Hasher, 2002). Accordingly, the manipulation checks showed that subjects were able to track the number of narratives reporting VAE, although there was some decline in accuracy when this number was larger. Nonetheless, results indicate that individuals perceived the absolute frequency of an uncertain event, yet extracted a relative frequency representation for subsequent risk judgments, as a change in total sample size did not affect the biasing influence of narrative information (RQ3).
This finding stands in contrast to some existing literature. Research on the ratio bias, for instance, would have predicted that subjects perceive a higher likelihood or risk when 8 of 20 narratives report VAE rather than 4 of 10, as they concentrate on the absolute frequency of the focal event and fail to take into account the total number of events (Denes-Raj & Epstein, 1994; Reyna & Brainerd, 2008). However, the occurrence of the ratio-bias appears to depend on within-subjects comparisons (Lefebvre, Vieider, & Villeval, 2010), whereas the present study used a between-subjects design.
Similarly, Obrecht et al. (2009) employed a within-subjects design in their encounter frequency account. However, while 4 of 10 and 8 of 20 narratives would result in equal ratios of positive and negative encounters, their theory hinges on the idea that the statistic enters the judgment process as simply one more instance indicating either the occurrence or non-occurrence of an event. This extra piece of information leads to differing ratios and, subsequently, differing predictions of perceived probability. There may be some merit to this theory if the statistic offers clear-cut evidence, i.e., the likelihood is extremely high or low. However, a probability of 20% clearly indicates a certain amount of risk; one would be hard-pressed to simply interpret it as a non-occurrence of an event because it is numerically below 50%.
Taken together, our findings indicate that subjects interpreted the narratives as representing one sample of events conveying a probability and the statistic as another such sample. We did observe two almost significant interaction effects of sample size: First, probability estimates were biased by the narrative information only when the sample was small. This might be due to a more accurate tracking of event frequencies when only ten exemplars were presented. Second, individuals high in numeracy showed no narrative bias on the risk measure in a small sample as compared to a large one. This might indicate that these subjects did in fact consider sample size in their judgments, as a larger sample of 20 events does have a higher diagnostic value than a smaller sample of 10 cases. As both effects were barely significant and rather small, we do not believe that they impede our previous reasoning.
We observed opposing effects of numeracy on the respective dependent measures in the two experiments. It is important to note, however, that we employed two different instruments to assess numeracy. The Subjective Numeracy Scale in Experiment 1 measures self-assessed ability and preferences to understand and apply numbers, whereas the combined test in Experiment 2 objectively assesses the ability to perform mathematical operations with percentages and proportions. Even though the former measure was developed to serve as a proxy for objective performance tests, inconsistent results have been observed previously. In addition, it has been shown recently that subjective and objective numeracy scales share only a limited amount of variance and differ in their predictions of various biases (Hess, Visschers & Siegrist, 2011; Liberali, Reyna, Furlan, Stein, & Pardo, 2012, Peters & Bjalkebring, 2014).
In Experiment 1, only the measures of subjective probability were affected by subjective numeracy, although in different ways. The statistical variation led to more extreme values on the 7-point rating scale for individuals higher in subjective numeracy, which implies a relation to the way individuals use a given scale for mapping likelihood. In contrast, higher subjective numeracy resulted in percent estimates that were less biased by narrative information, indicating significance for the process of integrating probabilities. In Experiment 2, we observed that objective numeracy decreased risk perceptions in general and moderated the narrative bias. Percent estimates of subjective probability were moderated only by objective numeracy when risk was assessed first, leading to a narrative bias in the first place.
The question of whether a unitary construct underlies the various observed effects or lack thereof has been an ongoing debate (e.g., Nelson, Moser, & Han, 2013; Reyna, Nelson, Han, & Dieckmann, 2009). Subjective numeracy appears to reflect motivation and confidence regarding the use of numerical information, i.e., it relates to how people approach a task. Thus, the lack of an effect on the risk measure in Experiment 1 is in line with our thinking that the risk judgments were approached in a more intuitive rather than rule-based manner. Of course, the processing of proportions is still relevant in the actual formation of a risk judgment, as the results regarding the sample size in Experiment 2 clearly demonstrate. Thus, the effect of objective numeracy, which appears to drive actual number operations, does not contradict the findings from Experiment 1. These findings support the notion of two related but not identical numeracy constructs (Peters & Bjalkebring, 2014).
We addressed two potential experimental artifacts as alternative explanations for the narrative bias that both relate to conversational norms. First, encoding of the individuating information is typically mandatory in experiments like this. Thus, subjects might assume that it is relevant to the task at hand and thus only use it for this reason (Grice, 1975). We offered subjects a choice and found that, when reading the narratives was optional, the narrative bias occurred just as strongly (r = .39, p < .01) as when it was required (r = .44, p < .01; RQ4).
Second, it has been argued that, when two conflicting pieces of information are presented, conversational norms indicate that the more informative and thus more important information is typically placed last (Krosnick at al., 1990). As the individuating information is generally presented after a base-rate in most related research, we varied the sequence of narrative and statistical information to exclude the possibility that the narrative bias is driven by recency. The results show that the narrative bias occurred independently of the narratives’ position in the sequence of information (RQ5).
Thus, we found no evidence in favor of the hypothesis that the narrative bias is based on adherence to conversational norms. On the other hand, we also cannot rule out their significance. Even in the optional encoding conditions, the narratives were still provided by the experimenter. Therefore, it is still possible that the subjects assumed that they are relevant for their judgments. The fact that nearly 80% of subjects chose to read the narratives in addition to the statistical information might support this interpretation.
Ultimately, the importance of conversational norms in research on cognitive biases due to irrelevant information cannot be ascertained conclusively in an experiment, as all information is always provided by the experimenter. However, the motivation of the majority of subjects to read the narratives in this experiment might be explained differently. Huber, Wider, and Huber (1997) found that individuals are often more interested in the outcomes of risky situations rather than the likelihood of negative outcomes. This behavior appears to have biological roots, as fish and birds behave in a similar manner. The costly information hypothesis states that when information (e.g., concerning vaccine safety) is too costly to be acquired personally (because it might harm the organism), animals will take advantage of the relatively low-cost information provided by others (Boyd & Richerson, 1985; Webster & Laland, 2008).
Taken together, narratives appear to represent an attractive source of information, as they deliver details on specific outcomes of risky situations (RQ6). Whether people deem them to be relevant for their risk assessments due to their specificity (see for example Bar-Hillel, 1980) or simply because they have been presented cannot be answered decisively. However, the fact that in the present research both procedural manipulations had no effect at all on risk perceptions renders experimental artifacts as sole drivers of the narrative bias less likely.
One goal of this study was to investigate the biasing effect of narrative information as a function of different self-report measures. However, a general concern in this line of research is a potential lack of external validity due to the use of hypothetical scenarios, meaning that presenting a bias incurs no cost to the subjects. Indeed, some biases have been found to decrease or disappear when payment is dependent on performance (Lefebvre et al., 2010). Future research should strive to substantiate the present findings by incentivizing non-biased judgments (Hertwig & Ortmann, 2001).
The data in Experiment 2 were collected through Amazon Mechanical Turk. The data quality may be affected by increased error variance if a greater number of subjects did not take their participation seriously. For this reason, we eliminated subjects whose time to complete the study suggested non-serious participation. Further, previous research has shown an advantage of Mechanical Turk samples in heterogeneity compared to the standard student sample as well as sufficient quality according to the psychometric publication standards (Buhrmester, Kwang & Gosling, 2011; Mason & Suri, 2012; Paolacci, Chandler & Ipeirotis, 2010).
The biasing effect of a small sample of single-case narratives is in part dependent on the measure used to assess it. Scales that gauge the likelihood dimension of an uncertain prospect are least affected. Narratives have the strongest effect on measures of a more extensive risk representation, which may entail a value dimension as well as other aspects, e.g., an affective appraisal of the uncertain event. This more comprehensive idea of a risk appears to be of greater importance in guiding decisions and behavior than a strict likelihood representation. On the other hand, judgments of subjective probability as well as of perceived risk appear to be ad hoc constructions and are therefore susceptible to wording and framing effects. Attempts to predict preferences and behavior should therefore be viewed cautiously, as risk perception might change from the time of assessment to the time of action due to a change of context. Further, systematic review or overview articles need to not only specify the exact wording and scale format of the instruments that were used in the original research but also take concomitant assessments of related constructs into account. Individuals do extract a representation of likelihood from single-case exemplars. This representation drives the narrative bias. However, the effect is much smaller on scales that assess only the perceived likelihood as compared to a measure of a broader and more intuitive concept of risk.
Taken together, these results underline the important conceptual distinction between judgments of subjective probability and perceived risk. When individuals judge a risk, they take many other aspects of the risky prospect into account than merely its probability of occurrence. Next to its severity, characteristics such as the voluntariness of, knowledge about, and control over risk play a role in risk perception. Affective reactions, personal susceptibility, and the source of a risk are additional potentially relevant factors. The measures we investigated reflect these different concepts to differing degrees. For instance, the perceived severity of VAE had no effect on percent estimates of probability, a small effect on a verbal probability measure, and a strong effect on a measure of risk.
However, the narrative bias we observed cannot be attributed to any of these additional aspects of risk, as they were either held constant across subjects, e.g., the emotionality of narratives, or controlled for through randomization. Further, Experiment 2 clearly indicates that the bias was driven by a representation of relative frequency, i.e., probability. This representation had small effects on measures of probability, i.e., instruments that are designed to solely assess this very representation. On the other hand, it had large effects on an inherently multidimensional measure of risk. Thus, we conclude that the relationship between representations of subjective probability and perceived risk is not yet fully understood. Future research should strive to understand what role likelihood representations play in the formation of risk perceptions.
Baghal, T. (2011). The measurement of risk perceptions: The case of smoking. Journal of Risk Research, 14(3), 351–364. http://dx.doi.org/10.1080/13669877.2010.541559.
Ball, D. J., & Watt, J. (2013). Further thoughts on the utility of risk matrices. Risk Analysis, 33(11), 2068–2078. http://dx.doi.org/10.1111/risa.12057.
Bar-Hillel, M. (1980). The base-rate fallacy in probability judgments. Acta Psychologica, 44(3), 211-233. http://dx.doi.org/10.1016/0001-6918(80)90046-3.
Baumeister, R. F., Bratslavsky, E., Finkenauer, C., & Vohs, K. D. (2001). Bad is stronger than good. Review of General Psychology, 5(4), 323–370. http://dx.doi.org/10.1037//1089-2680.5.4.323.
Beach, L. R., & Phillips, L. D. (1967). Subjective probabilities inferred from estimates and bets. Journal of Experimental Psychology, 75(3), 354–359. http://dx.doi.org/10.1037/h0025061.
Betsch, C., Brewer, N. T., Brocard, P., Davies, P., Gaissmaier, W., Haase, N., … Stryk, M. (2012). Opportunities and challenges of Web 2.0 for vaccination decisions. Vaccine, 30(25), 3727–3733. http://dx.doi.org/10.1016/j.vaccine.2012.02.025.
Betsch, C., Renkewitz, F., & Haase, N. (2013). Effect of narrative reports about vaccine adverse events and bias-awareness disclaimers on vaccine decisions: A simulation of an online patient social network. Medical Decision Making, 33(1), 14–25. http://dx.doi.org/10.1177/0272989X12452342.
Betsch, C., Ulshöfer, C., Renkewitz, F., & Betsch, T. (2011). The influence of narrative v. statistical information on perceiving vaccination risks. Medical Decision Making, 31(5), 742–753. http://dx.doi.org/10.1177/0272989X11400419.
Borgida, E., & Nisbett, R. (1977). The differential impact of abstract vs. concrete information on decisions. Journal of Applied Social Psychology, 7(3), 258–271. http://dx.doi.org/10.1111/j.1559-1816.1977.tb00750.x.
Boyd, R., & Richerson, P. J. (1985). Culture and the evolutionary process. Chicago: University of Chicago Press.
Brewer, N. T., Chapman, G. B., Gibbons, F. X., Gerrard, M., McCaul, K. D., & Weinstein, N. D. (2007). Meta-analysis of the relationship between risk perception and health behavior: The example of vaccination. Health Psychology, 26(2), 136–45. http://dx.doi.org/10.1037/0278-6133.26.2.136.
Brun, W. (1994). Risk perception: Main issues, approaches and findings. In G. Wright & P. Ayton (Eds.), Subjective probability (pp. 295–320). Chichester, England: Jon Wiley & Sons.
Buhrmester, M., Kwang, T., & Gosling, S. D. (2011). Amazon’s Mechanical Turk: A new source of inexpensive, yet high-quality, data? Perspectives on Psychological Science, 6(1), 3–5. http://dx.doi.org/10.1177/1745691610393980.
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Mahwah, NJ: Lawrence Erlbaum Associates Publishers.
Cokely, E. T., Galesic, M., Schulz, E., Ghazal, S., & Garcia-Retamero, R. (2012). Measuring risk literacy: The Berlin Numeracy Test. Judgment and Decision Making, 7(1), 25–47. Retrieved from http://journal.sjdm.org/11/11808/jdm11808.pdf.
de Wit, J. B. F., Das, E., & Vet, R. (2008). What works best: Objective statistics or a personal testimonial? An assessment of the persuasive effects of different types of message evidence on risk perception. Health Psychology, 27(1), 110–115. http://dx.doi.org/10.1037/0278-6133.27.1.110.
Denes-Raj, V., & Epstein, S. (1994). Conflict between intuitive and rational processing: When people behave against their better judgment. Journal of Personality and Social Psychology, 66(5), 819–829. http://dx.doi.org/10.1037/0022-3514.66.5.819.
Dieckmann, N. F., Slovic, P., & Peters, E. M. (2009). The use of narrative evidence and explicit likelihood by decisionmakers varying in numeracy. Risk Analysis, 29(10), 1473–1488. http://dx.doi.org/10.1111/j.1539-6924.2009.01279.x.
Eiser, J. R. (1994). Risk judgements reflect belief strength, not bias. Psychology and Health, 9(3), 197–199. http://dx.doi.org/10.1080/08870449408407479.
Fagerlin, A., Wang, C., & Ubel, P. A. (2005). Reducing the influence of anecdotal reasoning on people’s health care decisions: Is a picture worth a thousand statistics? Medical Decision Making, 25(4), 398–405. http://dx.doi.org/10.1177/0272989X05278931.
Fagerlin, A., Zikmund-Fisher, B. J., Ubel, P. A., Jankovic, A., Derry, H. A., & Smith, D. M. (2007). Measuring numeracy without a math test: Development of the Subjective Numeracy Scale. Medical Decision Making, 27(5), 672–680. http://dx.doi.org/10.1177/0272989X07304449.
Fox, S., & Duggan, M. (2013). Health online 2013. Retrieved from PEW Internet & American Life Project website: http://www.pewinternet.org/2013/01/15/health-online-2013.
Gardoni, P., & Murphy, C. (2013). A scale of risk. Risk Analysis, 34(7), 1208–1227. http://dx.doi.org/10.1111/risa.12150.
Gilovich, T., Griffin, D., & Kahneman, D. (Eds.). (2002). Heuristics and biases: The psychology of intuitive judgment. Cambridge, England: Cambridge University Press.
Goldstein, D. G., & Rothschild, D. (2014). Lay understanding of probability distributions. Judgment and Decision Making, 9(1), 1–14. Retrieved from http://journal.sjdm.org/13/131029/jdm131029.pdf.
Grice, H. P. (1975). Logic and conversation. In P. Cole & J. L. Morgan (Eds.) Syntax and semantics, 3: Speech acts (pp. 41–58). New York: Academic Press.
Haase, N. & Betsch, C. (2012). Parents trust other parents: Lay vaccination narratives on the web may create doubt about vaccination safety. Medical Decision Making, 32(4), 645. http://dx.doi.org/10.1177/0272989X12445286.
Haase, N., Renkewitz, F., & Betsch, C. (2013). The measurement of subjective probability: Evaluating the sensitivity and accuracy of various scales. Risk Analysis, 33(10), 1812–1828. http://dx.doi.org/10.1111/risa.12025.
Hasher, L., & Zacks, R. (1979). Automatic and effortful processes in memory. Journal of Experimental Psychology: General, 108(3), 356–388. http://dx.doi.org/10.1037/0096-3445.108.3.356.
Hertwig, R., & Ortmann, A. (2001). Experimental practices in economics: A methodological challenge for psychologists? Behavioral and Brain Sciences, 24(03), 383–403.
Hess, R., Visschers, V. H. M. & Siegrist, M. (2011). Risk communication with pictographs: The role of numeracy and graph processing. Judgment and Decision Making, 6(3), 263–274. Retrieved from http://journal.sjdm.org/11/10630/jdm10630.pdf.
Hinyard, L. J., & Kreuter, M. W. (2007). Using narrative communication as a tool for health behavior change: A conceptual, theoretical, and empirical overview. Health Education & Behavior, 34(5), 777–792. http://dx.doi.org/10.1177/1090198106291963.
Huber, O.,Wider, R., & Huber, O.W. (1997), Active information search and complete information presentation in naturalistic risky decision tasks. Acta Psychologica, 95(1), 15–29. http://dx.doi.org/10.1016/S0001-6918(96)00028-5.
Kata, A. (2010). A postmodern Pandora’s box: Anti-vaccination misinformation on the Internet. Vaccine, 28(7), 1709–1716. http://dx.doi.org/10.1016/j.vaccine.2009.12.022.
Kata, A. (2012). Anti-vaccine activists, Web 2.0, and the postmodern paradigm – An overview of tactics and tropes used online by the anti-vaccination movement. Vaccine, 30(25), 3778–3789. http://dx.doi.org/10.1016/j.vaccine.2011.11.112.
Keller, C., Siegrist, M., & Visschers, V. (2009). Effect of risk ladder format on risk perception in high- and low-numerate individuals. Risk Analysis, 29(9), 1255–1264. http://dx.doi.org/10.1111/j.1539-6924.2009.01261.x.
Knapp, P., Gardner, P. H., Raynor, D. K., Woolf, E., & McMillan, B. (2010). Perceived risk of tamoxifen side effects: A study of the use of absolute frequencies or frequency bands, with or without verbal descriptors. Patient Education and Counseling, 79(2), 267–271. http://dx.doi.org/10.1016/j.pec.2009.10.002.
Krosnick, J. A., Li, F., & Lehman, D. R. (1990). Conversational conventions, order of information acquisition, and the effect of base rates and individuating information on social judgments. Journal of Personality and Social Psychology, 59(6), 1140–1152. http://dx.doi.org/10.1037/0022-3514.59.6.1140.
Lee, S. W. S., Schwarz, N., Taubman, D., & Hou, M. (2010). Sneezing in times of a flu pandemic: Public sneezing increases perception of unrelated risks and shifts preferences for federal spending. Psychological Science, 21(3), 375–377. http://dx.doi.org/10.1177/0956797609359876.
Lefebvre, M., Vieider, F. M., & Villeval, M. C. (2010). The ratio bias phenomenon: Fact or artifact? Theory and Decision, 71(4), 615–641. http://dx.doi.org/10.1007/s11238-010-9212-9.
Liberali, J. M., Reyna, V. F., Furlan, S., Stein, L. M., & Pardo, S. T. (2012). Individual differences in numeracy and cognitive reflection, with implications for biases and fallacies in probability judgment. Journal of Behavioral Decision Making, 25(4), 361–381. http://dx.doi.org/10.1002/bdm.752.
Loewenstein, G. F., Weber, E. U., Hsee, C. K., & Welch, N. (2001). Risk as feelings. Psychological Bulletin, 127(2), 267–286. http://dx.doi.org/10.1037//0033-2909.127.2.267.
Mason, W., & Suri, S. (2012). Conducting behavioral research on Amazon’s Mechanical Turk. Behavior Research Methods, 44(1), 1–23. http://dx.doi.org/10.3758/s13428-011-0124-6.
Nelson, W. L., Moser, R. P., & Han, P. K. J. (2013). Exploring objective and subjective numeracy at a population level: Findings from the 2007 Health Information National Trends Survey (HINTS). Journal of Health Communication, 18(2), 192–205. http://dx.doi.org/10.1080/10810730.2012.688450.
Obrecht, N. A., Chapman, G. B., & Gelman, R. (2009). An encounter frequency account of how experience affects likelihood estimation. Memory & Cognition, 37(5), 632–643. http://dx.doi.org/10.3758/MC.37.5.632.
Paolacci, G., Chandler, J., & Ipeirotis, P. G. (2010). Running experiments on Amazon Mechanical Turk. Judgment and Decision Making, 5(5), 411–419. Retrieved from http://journal.sjdm.org/10/10630a/jdm10630a.pdf.
Peters, E. (2008). Numeracy and the perception and communication of risk. Annals of the New York Academy of Sciences, 1128, 1–7. http://dx.doi.org/10.1196/annals.1399.001.
Peters, E. & Bjalkebring, P. (2014). Multiple numeric competencies: When a number is not just a number. Journal of Personality and Social Psychology. Advance online publication. http://dx.doi.org/10.1037/pspp0000019.
Reyna, V. F. (2008). A theory of medical decision making and health: Fuzzy trace theory. Medical Decision Making, 28(6), 850–865. http://dx.doi.org/10.1177/0272989X08327066.
Reyna, V. F. (2012). Risk perception and communication in vaccination decisions: a fuzzy-trace theory approach. Vaccine, 30(25), 3790–3797. http://dx.doi.org/10.1016/j.vaccine.2011.11.070.
Reyna, V. F., & Brainerd, C. J. (2008). Numeracy, ratio bias, and denominator neglect in judgments of risk and probability. Learning and Individual Differences, 18(1), 89–107. http://dx.doi.org/10.1016/j.lindif.2007.03.011.
Reyna, V. F., Nelson, W. L., Han, P. K., & Dieckmann, N. F. (2009). How numeracy influences risk comprehension and medical decision making. Psychological Bulletin, 135(6), 943–973. http://dx.doi.org/10.1037/a0017327.
Rozin, P., & Royzman, E. B. (2001). Negativity bias, negativity dominance, and contagion. Personality and Social Psychology Review, 5(4), 296–320. http://dx.doi.org/10.1207/S15327957PSPR0504\_2.
Schwartz, L. M. L., Woloshin, S. S., Black, W. C. W., & Welch, H. G. H. (1997). The role of numeracy in understanding the benefit of screening mammography. Annals of Internal Medicine, 127(11), 966–972. http://dx.doi.org/10.7326/0003-4819-127-11-199712010-00003.
Schwarz, N. (1999). Self-reports: How the questions shape the answers. American Psychologist, 54(2), 93–105. http://dx.doi.org/10.1037/0003-066X.54.2.93.
Schwarz, N. (2007). Cognitive aspects of survey methodology. Applied Cognitive Psychology, 21(2), 277–287. http://dx.doi.org/10.1002/acp.1340.
Siegrist, M., & Cvetkovich, G. (2001). Better negative than positive? Evidence of a bias for negative information about possible health dangers. Risk Analysis, 21(1), 199–206. http://dx.doi.org/10.1111/0272-4332.211102.
Skowronski, J. J., & Carlston, D. E. (1989). Negativity and extremity biases in impression formation: A review of explanations. Psychological Bulletin, 105(1), 131–142. http://dx.doi.org/10.1037/0033-2909.105.1.131.
Slovic, P., Finucane, M. L., Peters, E., & MacGregor, D. G. (2004). Risk as analysis and risk as feelings: Some thoughts about affect, reason, risk, and rationality. Risk Analysis, 24(2), 311–322. http://dx.doi.org/10.1111/j.0272-4332.2004.00433.x.
Slovic, P., Fischhoff, B, & Lichtenstein, S. (1979). Rating the risks. Environment, 21(3), 14-20, 36-39.
Ubel, P. A., Jepson, C., & Baron, J. (2001). The inclusion of patient testimonials in decision aids effects on treatment choices. Medical Decision Making, 21(1), 60–68. http://dx.doi.org/10.1177/0272989X0102100108.
van Gelder, J.-L., de Vries, R. E., & van der Pligt, J. (2009). Evaluating a dual-process model of risk: Affect and cognition as determinants of risky choice. Journal of Behavioral Decision Making, 22(1), 45–61. http://dx.doi.org/10.1002/bdm.610.
Weber, E., & Hilton, D. (1990). Contextual effects in the interpretations of probability words: Perceived base rate and severity of events. Journal of Experimental Psychology: Human Perception and Performance, 16(4), 781–789. http://dx.doi.org/10.1037/0096-1523.16.4.781.
Webster, M. M., & Laland, K. N. (2008). Social learning strategies and predation risk: Minnows copy only when using private information would be costly. Proceedings of the Royal Society B: Biological Sciences, 275(1653), 2869–2876. http://dx.doi.org/10.1098/rspb.2008.0817.
Weinstein, N. D., & Diefenbach, M. A. (1997). Percentage and verbal category measures of risk likelihood. Health Education Research, 12(1), 139–141. http://dx.doi.org/10.1093/her/12.1.139.
Weinstein, N. D., Kwitel, A., McCaul, K. D., Magnan, R. E., Gerrard, M., & Gibbons, F. X. (2007). Risk perceptions: Assessment and relationship to influenza vaccination. Health Psychology, 26(2), 146–151. http://dx.doi.org/10.1037/0278-6133.26.2.146.
Windschitl, P. D. (2002). Judging the accuracy of a likelihood judgment: The case of smoking risk. Journal of Behavioral Decision Making, 15(1), 19–35. http://dx.doi.org/10.1002/bdm.401.
Windschitl, P. D., Martin, R., & Flugstad, A. R. (2002). Context and the interpretation of likelihood information: The role of intergroup comparisons on perceived vulnerability. Journal of Personality and Social Psychology, 82(5), 742–755. http://dx.doi.org/10.1037//0022-3514.82.5.742.
Windschitl, P. D., & Wells, G. L. (1996). Measuring psychological uncertainty: Verbal versus numeric methods. Journal of Experimental Psychology: Applied, 2(4), 343–364. http://dx.doi.org/10.1037//1076-898X.2.4.343.
Zacks, R. T., & Hasher, L. (2002). Frequency processing: A twenty-five year perspective. In P. Sedlmeier & T. Betsch (Eds.), Etc. Frequency processing and cognition (pp. 21–36). Oxford, England: University Press.
Note that in Experiment 1 the materials were in German.
Hi everyone! Well I just got my dysomeria shot at my family doctor’s office in town. I got an appointment right away and had no adverse effects whatsoever. Everything went just fine and was easy. So, all in all, no reason to complain or worry. John
My doctor had told me that I should get vaccinated against dysomeria. Well I’m not really a fan of needles, but last week I just went and got it over with. Afterwards: no problems at all and I actually went to the gym to do my regular work out right afterwards. No biggie. Sarah
Well, I went to the doctor a week ago to get my dysomeria immunization. Usually I’m not very fragile but after this shot I felt dizzy for days and could hardly ride my bike. Let me tell you, not very appealing to constantly stagger trying not to fall over all the time! Julie
I had about a week of fever after my dysomeria vaccination. I do not know if that was a side effect but I was confined to the bed for quite a while and could hardly move a muscle. I’m just glad it’s over now and I can get back to normal life. Bill
Correlations between independent variables and numeracy and the
respective dependent variable for each subsample in Experiment 1. For
example: When perceived risk was the first dependent measure, the
correlation between judgments of perceived risk and the frequency of
positive narratives was r = .66, p < .001 in
the 5% base-rate condition and r = .29,
p < .05 in the 40% base-rate condition.
| Subjective probability (percent estimate) | ||||
n | Statistical base-rate (5% vs. 40%) | Narratives: frequency of VAE (5% vs. 40%) | Subjective numeracy | |
Statistical base-rate: 5% | 44 | — | .27† | -.21 |
Statistical base-rate: 40% | 45 | — | .25 | .11 |
Narratives: frequency of VAE: 5% | 44 | .84*** | — | -.06 |
Narratives: frequency of VAE: 40% | 45 | .80*** | — | -.12 |
Overall | 89 | .81*** | .16 | -.07 |
| Subjective probability (7-point rating scale) | ||||
n | Statistical base-rate (5% vs. 40%) | Narratives: frequency of VAE (5% vs. 40%) | Subjective numeracy | |
Statistical base-rate: 5% | 47 | — | .12 | -.26† |
Statistical base-rate: 40% | 47 | — | .24† | .23 |
Narratives: frequency of VAE: 5% | 47 | .50*** | — | -.12 |
Narratives: frequency of VAE: 40% | 47 | .64*** | — | -.10 |
Overall | 94 | .56*** | .17 | -.07 |
| Perceived risk (visual analog scale) | ||||
n | Statistical base-rate (5% vs. 40%) | Narratives: frequency of VAE (5% vs. 40%) | Subjective numeracy | |
Statistical base-rate: 5% | 44 | — | .66*** | -.08 |
Statistical base-rate: 40% | 50 | — | .29* | .09 |
Narratives: frequency of VAE: 5% | 45 | .47** | — | .03 |
Narratives: frequency of VAE: 40% | 49 | .18 | — | -.02 |
Overall | 94 | .30** | .44*** | -.001 |
| *p < .05, two-tailed. **p < .01, two-tailed. ***p < .001, two-tailed. †p < .05, one-tailed. | ||||
Correlations between independent variables and numeracy and the
respective dependent variable for each subsample in Experiment 2.
| Subjective probability (percent estimate) | ||||
n | Sample size (10 vs. 20) | Narratives: frequency of VAE (10% vs. 20% vs. 40%) | Numeracy | |
Sample size: 10 | 88 | — | .23* | -.09 |
Sample size: 20 | 93 | — | -.04 | .03 |
Narratives: frequency of VAE: 10% | 61 | .12 | — | .09 |
Narratives: frequency of VAE: 20% | 61 | -.10 | — | -.06 |
Narratives: frequency of VAE: 40% | 59 | -.19 | — | -.17 |
Overall | 181 | -.04 | .10 | -.04 |
| Perceived risk (visual analog scale) | ||||
n | Sample size (10 vs. 20) | Narratives: frequency of VAE (10% vs. 20% vs. 40%) | Numeracy | |
Sample size: 10 | 83 | — | .31** | -.11 |
Sample size: 20 | 85 | — | .46*** | -.17 |
Narratives: frequency of VAE: 10% | 55 | .07 | — | -.08 |
Narratives: frequency of VAE: 20% | 60 | -.31* | — | -.02 |
Narratives: frequency of VAE: 40% | 53 | .05 | — | -.27* |
Overall | 168 | -.07 | .38*** | -.14† |
| *p < .05, two-tailed. **p < .01, two-tailed. ***p < .001, two-tailed. †p < .05, one-tailed. | ||||
Correlations between subjective probability (percent estimate, 7-point
rating scale), perceived risk, and intention to get vaccinated for the
full sample and the respective subsamples in Experiment 1.
| Full sample | ||||
| N = 277 | Percent | 7-point | Risk | Intention |
Percent | — | |||
7-point | .70*** | — | ||
Risk | .61*** | .74*** | — | |
Intention | -.22*** | -.34*** | -.43*** | — |
| Subjective probability (percent estimate) | ||||
| n = 89 | Percent | 7-point | Risk | Intention |
Percent | — | |||
7-point | .75*** | — | ||
Risk | .69*** | .83*** | — | |
Intention | -.31** | -.42*** | -.47*** | — |
| Subjective probability (7-point rating scale) | ||||
| n = 94 | Percent | 7-point | Risk | Intention |
Percent | — | |||
7-point | .66*** | — | ||
Risk | .64*** | .74*** | — | |
Intention | -.24* | -.33** | -.53*** | — |
| Perceived risk (visual analog scale) | ||||
| n = 94 | Percent | 7-point | Risk | Intention |
Percent | — | |||
7-point | .69*** | — | ||
Risk | .49*** | .64*** | — | |
Intention | -.11 | -.28** | -.31** | — |
| Note. The correlation matrix for the full sample is included again (see Table 3) to facilitate comparison. | ||||
| *p < .05. **p < .01. ***p < .001. | ||||
Correlations between subjective probability, perceived risk, and
intention to get vaccinated for the full sample and the respective
subsamples in Experiment 2.
| Full sample | |||
| N = 464 | Percent | Risk | Intention |
Percent | — | ||
Risk | .22*** | — | |
Intention | .01 | -.41*** | — |
| Subjective probability (percent estimate) | |||
| n = 181 | Percent | Risk | Intention |
Percent | — | ||
Risk | .05 | — | |
Intention | .02 | -.48*** | — |
| Perceived risk (visual analog scale) | |||
| n = 283 | Percent | Risk | Intention |
Percent | — | ||
Risk | .31*** | — | |
Intention | -.004 | -.37*** | — |
| Note. The subsample that judged perceived risk first includes the subjects from the two subdesigns. | |||
| *p < .05. **p < .01. ***p < .001. | |||
Copyright: © 2015. The authors license this article under the terms of the Creative Commons Attribution 3.0 License.
This document was translated from LATEX by HEVEA.