Judgment and Decision Making, Vol. 13, No. 1, 2018, pp. 79-98
Stepwise training supports strategic second-order theory of mind
in turn-taking gamesRineke Verbrugge*
Ben Meijering#
Stefan Wierda$
Hedderik van RijnX
Niels TaatgenY |
People model other people’s mental states in order to understand and
predict their behavior. Sometimes they model what others think about
them as well: “He thinks that I intend to stop.” Such second-order
theory of mind is needed to navigate some social situations, for
example, to make optimal decisions in turn-taking games. Adults
sometimes find this very difficult. Sometimes they make decisions
that do not fit their predictions about the other player. However,
the main bottleneck for decision makers is to take a second-order
perspective required to make a correct opponent model. We report a
methodical investigation into supporting factors that help adults do
better. We presented subjects with two-player, three-turn games in
which optimal decisions required second-order theory of mind (Hedden
and Zhang, 2002). We applied three “scaffolds” that,
theoretically, should facilitate second-order perspective-taking: 1)
stepwise training, from simple one-person games to games requiring
second-order theory of mind; 2) prompting subjects to predict the
opponent’s next decision before making their own decision; and 3) a
realistic visual task representation. The performance of subjects in
the eight resulting combinations shows that stepwise training, but
not the other two scaffolds, improves subjects’ second-order
opponent models and thereby their own decisions.
Keywords: decision making, second-order theory of mind, opponent modeling, scaffolding, turn-taking games, sequential games, centipede, strategic reasoning, perfect-information games
1 Introduction
Why is it that, while we are often told to put ourselves into another
person’s shoes, we fail to do so when it’s most needed? Consider the
Camp David negotiations in 1978. Egypt’s President Sadat first
presented a tough official proposal, but then wrote a much friendlier
informal letter to the mediator, US President Carter. This letter
contained his fallback positions about the issues on the table. Even
though Carter did not tell the exact contents of this letter to
Israel’s President, Begin still knew about its existence. Sadat failed
to wonder about the crucial question: “Does Begin know that
Carter knows my fallback positions?” Begin used his knowledge
by pushing towards Sadat’s fallback positions in the further
negotiations and he made sure that everyone knew that the
Israeli parliament would not allow Begin to make any concessions
on the Palestinian question, which was ultimately left unresolved in
the final Camp David Accords (Telhami, 1992; Oakman, 2002). What was
Sadat missing?
Many of our daily social interactions also require the ability to
infer another person’s knowledge, beliefs, desires, and
intentions. For example, if we are trying to sell our house, we are
reasoning about whether the potential buyer knows that we already
bought a new house. The ability to put ourselves in other people’s
shoes and reason about their beliefs, knowledge, plans and intentions,
which may differ from our own, is called theory of mind
(henceforth usually ToM, coined by (Premack and Woodruff, 1978)). To be more
specific, we use first-order theory of mind to ascribe a simple
mental state about world facts to someone, for example: “Ann believes that I wrote this novel under pseudonym, but in fact I did
not.” This ability to make correct first-order attributions is
apparent around the age of 4 (Wellman, Cross and Watson, 2001; Wimmer and Perner, 1983). Second-order theory of mind adds an extra layer of mental state
attribution, as in: “Bob doesn’t know that I know that he
is the pseudonymous author of this novel.”
Second-order ToM is indispensable in a host of social situations. It
is needed in communication to understand politeness, humor, irony,
faux pas, and lying
(Filippova and Astington, 2008; Talwar, Gordon and Lee, 2007; Hsu and Cheung, 2013). Second-order ToM is also
needed to make correct decisions in strategic interactions, for
example, to win competitive games and to propose offers that lead to
win-win solutions in negotiations, as has been shown using agent
simulations (Weerd, Verbrugge and Verheij, 2013, 2017).1 So it is a very useful
ability, but it is also very hard, and it appears to be developed
rather late in childhood.
1.1 Theory of mind is hard: communication, judgment and decision making
Second-order theory of mind starts to appear between the ages of
five and seven, when children start to correctly answer second-order
false belief questions such as “Where does Mary think that John will
look for the chocolate?” about a story in which John peeked in though
a window and saw Mary moving John’s piece of chocolate from the drawer
to the toybox, while Mary wasn’t aware that John had seen her in the
act (Perner and Wimmer, 1985; Sullivan, Zaitchik and Tager-Flusberg, 1994; Arslan, Hohenberger and Verbrugge, 2017). This ability continues
to develop during adolescence. Typical adults often display a
reasonable understanding of up to fourth-order mental state
attributions in stories, e.g. “Alice thinks that Bob doesn’t know
that she knows that he knows that she sent him an anonymous Valentine
card” (Kinderman, Dunbar and Bentall, 1998).2
However, in social situations, even adults may fail to take
other people’s perspectives into account. For example in
communication, a hearer often doesn’t realize that a speaker cannot
see some of the objects that the hearer can see (Lin, Keysar and Epley, 2010). Also,
when people are asked to make judgements about other people’s problem
solving skills, they often fail to apply useful cues such as speed of
answering (Mata and Almeida, 2014).
In the “Beauty Contest”, all subjects simultaneously have to pick
among 1,…, 100 the number they believe will be closest to 2/3 of
the average of all subjects’ choices. Many people guess 33, which
is 2/3 times the average of 1,…,100, thus not taking the
perspective of other subjects. Fewer people do use theory of mind
and choose at most 22, which is 2/3 times 33
(Nagel, 1995; Camerer, Ho and Chong, 2015).
Limited use of theory of mind among adults has also been shown in
social dilemmas such as the public goods game and the prisoner’s
dilemma (Colman, 2003; Kieslich and Hilbig, 2014; Rubinstein and Salant, 2016), the trust game
(Evans and Krueger, 2011, 2014), and one-shot games such as hide-and-seek,
matching pennies and the Mod game
(Devaine, Hollard and Daunizeau, 2014a, b; Frey and Goldstone, 2013; Weerd, Diepgrond and Verbrugge, 2017). In all
these games, subjects’ decisions in experiments do not fit with the
game-theoretically optimal predicted decision based on common
knowledge of rationality, the computation of which requires at least
second-order theory of mind.3
1.2 ToM in turn-taking games is hard, too
Particularly difficult tasks requiring theory of mind are turn-taking games, also called sequential games or dynamic
games. For example, in chess, players have to reason about what their
opponents would do in their next move, where the opponent in turn
thinks about the first player. Chess is a typical turn-taking game
where black and white alternate moves; it is also a perfect- and
complete-information game in the sense that both players know the
history and rules of the game, in contrast to a game like bridge, in
which players cannot see one another’s cards. Turn-taking games can be
represented by extensive form game trees (see
Figures 1 and 2).
So far, a number of turn-taking games of perfect and complete
information have been investigated. Games that require second-order
theory of mind to make optimal decisions appear to be especially
difficult. Whereas 8 year old children already perform at ceiling in
second-order false belief story understanding, they start to apply
second-order theory of mind in turn-taking games only when they are
between 8 and 10 years old, and even then their decisions are on
average only slightly better than chance level
(Flobbe et al., 2008; Raijmakers et al., 2014; Meijering et al., 2014; Arslan et al., 2015).
Even adults are slow to take the perspective of the opponent, let
alone to accurately model what their opponent thinks about them, in
turn-taking games such as the centipede game and sequential bargaining
(Johnson et al., 2002; Bicchieri, 1989; McKelvey and Palfrey, 1992; Kawagoe and Takizawa, 2012; Ghosh et al., 2017; Bhatt and Camerer, 2005; Camerer, Ho and Chong, 2015; Nagel and Tang, 1998; Ho and Su, 2013).
Hedden and Zhang (2002) found that participants on average start with a
default, myopic (first-order) theory-of-mind model of the opponent, though
the depth of such mental model may be adjusted according to their opponent?s
type upon their continued interactions. Zhang, Hedden and Chia (2012)
further manipulated perspective taking and showed (p.567) that there is a
cost of a factor of 0.65 in terms of likelihood of engaging in second-order
versus first-order theory-of-mind reasoning.
All these empirical results contradict the prescription of game theory that
players, on the basis of common knowledge of their rationality, apply
backward induction (Osborne and Rubenstein, 1994), which we now explain.
Backward induction
In the typical extensive form game tree of Figure
1, backward induction would run as
follows. Player 1 is rational, so at the final decision node, he would
decide to go down to C, because his payoff of 2 there is larger than
his payoff of 1 in D. Therefore, we can replace the final decision
node and its two children by the node (2,1). Taking Player 1’s
rationality into account, at the second decision point, a rational
Player 2 would decide to go down to B, because her payoff of 3 there
is larger than her payoff of 1 in the node (2,1). So we can replace
the second decision point and its children by the node (4,3). Finally,
at the first decision point, the rational Player 1, believing
that Player 2 believes that Player 1 is rational, would decide
to move to the right, because his payoff of 4 in the node (4,3) is
larger than the payoff of 3 that he would receive if ending the game
at A.
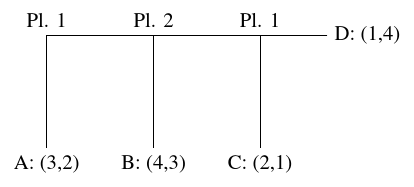
| Figure 1: Decision tree for an example turn-taking game in which Player 1 chooses first; if he chooses to go right, then Player 2 chooses, and if Player 2 also chooses to go right, finally Player 1 decides again. The pairs at the leaves A, B, C, and D represent the payoffs of Player 1 and Player 2, respectively. This payoff structure corresponds to the Marble Drop game of Figure 5 (c). Figure adapted from Figure 2 of (Rosenthal, 1981) and Figure 1 of (Hedden & Zhang, 2002) |
In summary, reasoning from the end at the right to the beginning of
the game, Player 1 deletes non-optimal actions, one by one. Note that
the Backward Induction concept requires both players to reason about
what would happen at each possible node, even if that node is never
reached in practice (Bicchieri, 1989). But do people really do so?
One paradigm to study how people actually reason in turn-taking games
is the Matrix Game, which will also be the base game in our
experiment.
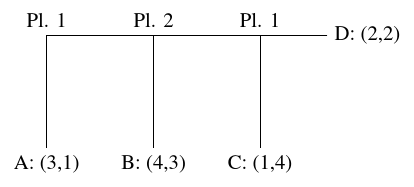
| Figure 2: Decision tree with a payoff structure corresponding to the Matrix Game of Figure 3 |
The Matrix Game
The Matrix Game is a turn-taking game between Player 1 and Player 2,
introduced by (Hedden and Zhang, 2002). A typical example can be found in
Figure 3. Each of four cells named A, B, C, and D contains a pair of
rewards, so-called payoffs. In each cell, the left number in the
payoff pair is Player 1’s payoff and the right number is Player 2’s
payoff if the game were to end up in that cell. For both players,
their payoffs in cells A, B, C, D range over the numbers 1, 2, 3, 4
and are all different, that is, there are no relevant payoff
ties. Each game starts at cell A. Both players alternately decide
whether to stay in the current cell or to move on to the next one. In
particular, Player 1 decides whether to stay in cell A or to go to
cell B. If the game has not ended yet, Player 2 then decides whether
to stay in cell B or to move to cell C. If the game still has not
ended, Player 1 finally decides whether to stay in cell C or to move
to D. The goal of Player 1 is that the game ends in a cell in which
the left payoff is as high as possible, while the goal of Player 2 is
that the game ends in a cell in which the right payoff is as high as
possible. Thus, both players have a self-interested goal, namely, to
maximize their own payoff in the cell in which the game ends
up. Unlike many competitive games, it is not a goal to win more points
than the opponent and maximize the difference. And, unlike cooperative
tasks, it is not a goal to maximize the sum of both players’ payoffs.
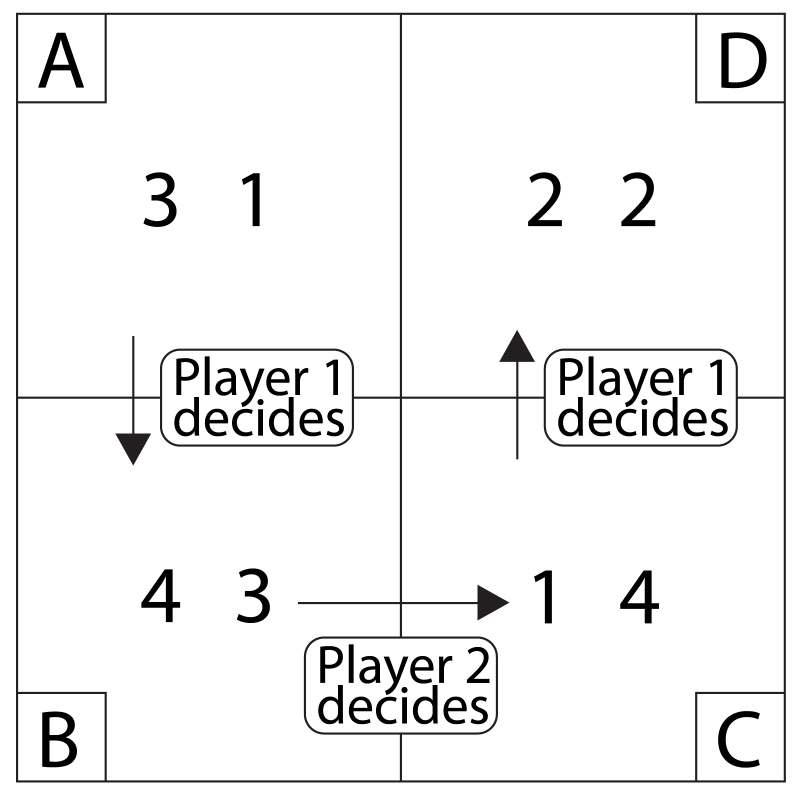
| Figure 3: The Matrix Game. Figure adapted from Figure 2 of (Hedden & Zhang, 2002) |
Still, when making their own decisions, players do have to reason
about each other. At cell A in the Matrix Game of Figure 3, Player 1
could correctly reason about a rational opponent: “Player 2 believes that I intend to move to cell D at my last decision
point, because my payoff there is higher than in cell C. At D,
however, Player 2 only wins a payoff of 2, so he intends to stay
at B in order to get the higher payoff 3. But that is excellent for
me, because ending up at B will give me a payoff of 4. Therefore, I
decide to move on to B.”
Adults have trouble making the correct mental model of the other
player (Hedden and Zhang, 2002; Zhang, Hedden and Chia, 2012): The proportion of games in which
subjects made correct second-order predictions about their
opponent was only 60%–70%, even at the end of the cited
experiments.4 Adolescents and young adults have an even harder time
playing the Matrix Game if they are sequentially pitted against
against both “myopic” (zero-order ToM) and ‘predictive’ (first-order
ToM) opponents (Li, Liu and Zhu, 2011).
1.3 Supporting strategic second-order ToM
We present an experiment to investigate how adults can best be
supported in applying second-order theory of mind in games with three
decisions such as the Matrix Game. Advantages of these games are that
it is possible to construct games of different levels of complexity in
terms of required theory of mind and to develop an idea of
subjects’ reasoning strategies on the basis of their mistakes.
In order to correctly gauge subjects’ level of theory of mind from
their decisions, we need to test them in a large number of different
game items, so that they cannot find an optimal solution just by
pattern recognition alone. Fortunately, for the Matrix Game, it is
possible to devise many different payoff distributions that require
such second-order perspective taking on the part of Player 1, who
wants to make an optimal decision at the start of the game.
Controlling the opponent’s decisions
If we want to support people in their second-order theory of mind, it
is important to control the strategy and the level of theory of mind
used by the opponent: A subject displays second-order theory of
mind by making a correct mental model of a first-order opponent. To
achieve this, many researchers use a human confederate of the
experimenter, who strictly follows pre-determined strategies
(Hedden and Zhang, 2002; Zhang, Hedden and Chia, 2012; Li, Liu and Zhu, 2011; Goodie, Doshi and Young, 2012). In many studies,
subjects play against a computer opponent. In such cases, they are
sometimes deceived by a story that they are playing against another
human being (Hedden and Zhang, 2002); other times, they are told that they
are playing “against four different players”
(Devaine, Hollard and Daunizeau, 2014a); at the most honest end of the spectrum,
subjects are told that they are playing against a very smart computer
opponent, possibly including information about the opponent’s
rationality or level of perspective taking
(Hedden and Zhang, 2002; Weerd, Verbrugge and Verheij, 2017; Ghosh et al., 2017). We choose the honest procedure
here.5
Scaffolding new skills
Wood and colleagues introduced the term “scaffolding” to describe the
types of support that an adult or expert could give to a child that
initially is not able to solve a problem or perform a task: “This
scaffolding consists essentially of the adult ‘controlling’ those
elements of the task that are initially beyond the learner’s capacity,
thus permitting him to concentrate upon and complete only those
elements that are within his range of competence”
(Wood, Bruner and Ross, 1976, p. 90). Recently, scaffolding has also been used in
the context of adults learning new skills (Clark, 1997), as we will
do here.6
In our experiment, we attempt to support subjects’ strategic
second-order theory of mind by three different scaffolds:
-
Stepwise training (compared to Undifferentiated training);
- Prompting them for predictions of their opponent’s next decision
(compared to No prompts);
- using a more intuitive visual Task representation called Marble
Drop (compared to the Matrix Game).
In the next section, we explain the three scaffolds in detail as well
as the a priori reasons why they may be helpful. We also
discuss the methods of the experiment. In Section 3, we present the
results and explain which factors (alone or together) influence the
performance of decision makers in the two-player turn-taking games. In
Section 4, we zoom in both on the kinds of mistakes subjects made
and on the reasoning strategies underlying their optimal decisions. We
conclude with some suggestions for possible future experiments on
de-biasing decision makers.
2 Method
2.1 Subjects
Ninety-three first-year psychology students (63 female) with a mean
age of 21 years (ranging between 18 and 31 years) participated in
exchange for course credit. All subjects had normal or
corrected-to-normal visual acuity.
One subject was excluded due to an error
in the experimental setup.
2.2 Design
The experimental design comprised three factors: training, prompting
predictions, and task representation. All factors were administered to
93 subjects in a 2 × 2 × 2 between-subject design, with
Stepwise/Undifferentiated training crossed with Prompt/No-Prompt
crossed with Marble-Drop/Matrix-Game.7 The experiment consisted of three blocks: one training
block followed by two test blocks. We now proceed to explain the three
factors training, prompting predictions, and task representation in
detail, and to explain a priori why each of the three manipulations
should provide the kind scaffolding discussed in the Introduction, to
support decision makers in their second-order theory of mind and in
making optimal decisions in the games.
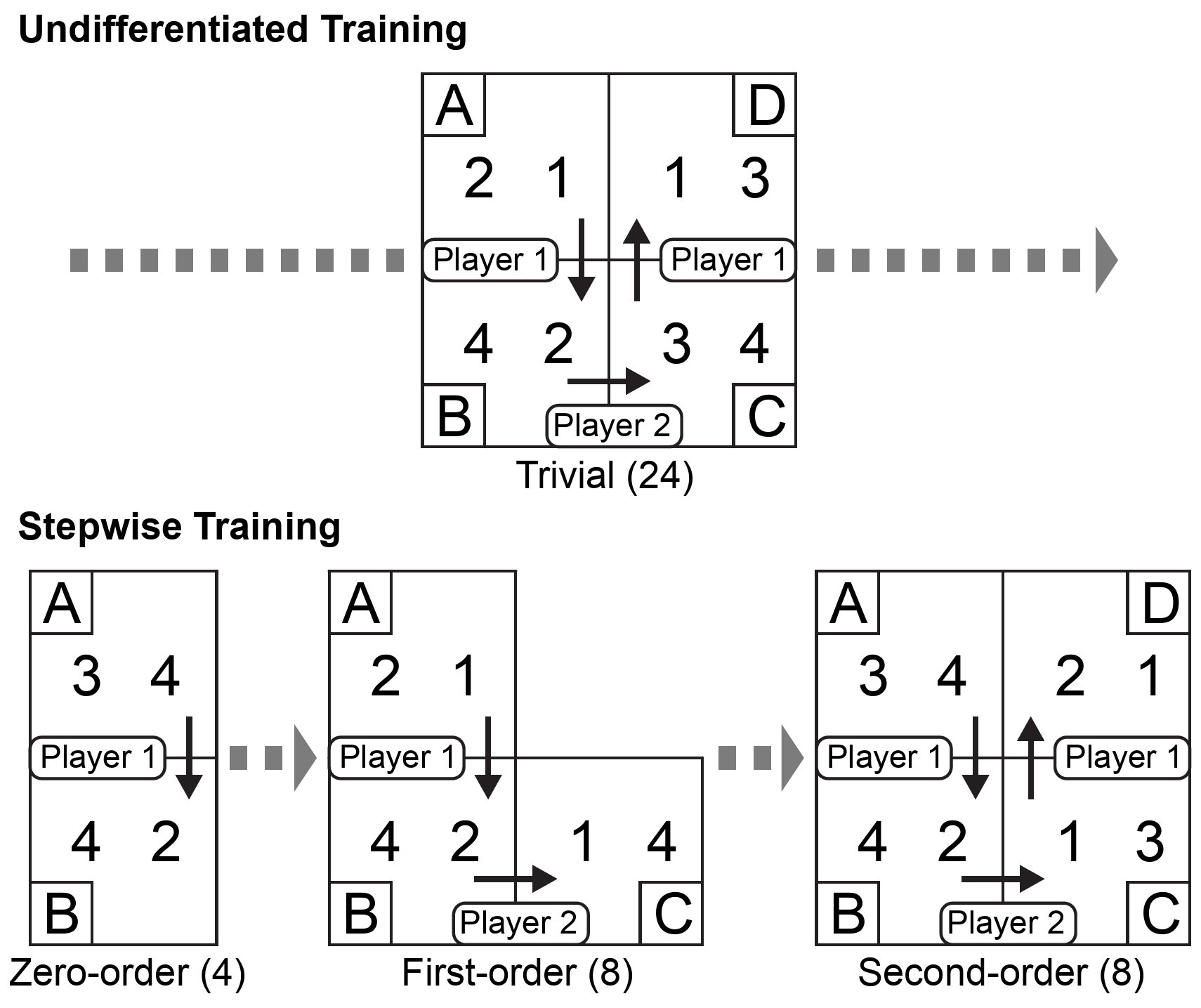
| Figure 4: Schematic overview of the Undifferentiated and Stepwise
training procedures for the Matrix Game. Undifferentiated training
consists of 24 different so-called trivial games (top panel, see
Subsection 2.3 for explanation). Stepwise training consists
of 4 zero-order games, 8 first-order games, and 8 second-order
games. The actual 20 training items all had different payoff
distributions (bottom panel). |
2.3 Scaffold 1: Training
The training block was included to familiarize subjects with the rules
of the games. Subjects were randomly assigned to one of two training
procedures. In one training procedure, subjects were presented with
Hedden and Zhang’s (2002) 24 original training games (see Figure
4; top panel). These so-called “trivial” training
games are easier to play than truly second-order games such as in the
game on the bottom right in Figure 4, because Player
2 does not have to reason about Player 1’s last possible decision:
Player 2’s payoff in B is either lower or higher than both his payoffs
in C and D. For example, in the game in the upper panel of Figure
4, to make an optimal decision, it suffices for the
subject to make the following correct first-order attribution: “The
other player intends to move from B to C, because his goal
is to earn as many points as possible, and in both C (3 points) and D
(4 points), he will receive more points than if he stays in B (2
points).”
This training procedure will henceforth be referred to as Undifferentiated training, because all 24 training games of this
type are of the same kind: they have three decision points while only
requiring first-order theory of mind. Possibly, these trivial games in
the training block made the change to the test blocks difficult for
the subjects of (Hedden and Zhang, 2002), who were suddenly required to
perform second-order perspective taking in order to make optimal
decisions in the Matrix Games.
In the other training procedure, which we name Stepwise
training, subjects were therefore presented with three blocks of
games that are simple at first and become increasingly more complex
with each block, subsequently requiring zero-order, first-order, and
second-order theory of mind to find the optimal decision (see Figure
4; bottom panel). More precisely, the first training
block of Stepwise training consisted of 4 games with just one decision
point. These games are so-called zero-order games, because they do not
require application of ToM. The second training block consisted of 8
games with two decision points. These games require application of
first-order ToM, for example, in Figure 4 (middle of bottom panel):
“The opponent intends to move from B to C, because his goal is to earn as many points as possible and 4 > 2”.
The third training block consisted of 8 games with three decision
points that require application of second-order ToM, because the
subject has to reason about the other player, and take into account
that the other player is reasoning about them. The subject could make
the following second-order attribution to the opponent: “The opponent
thinks that I intend to move from C to D, because he knows that my goal is to earn as many points as possible, and
2 > 1”. The pay-off structures in the 8 games of this third training
block were chosen in such a way that they were diagnostic of
second-order ToM reasoning, in the sense that first-order ToM
reasoning does not lead to an optimal solution for them, unlike in the
Undifferentiated training games. (See Appendix C for more explanation
of our selection of payoff structures.)
We hypothesize a priori that the Stepwise training procedure
provides scaffolding to support the representation of increasingly
more complex mental states. Stepwise introduction, explanation, and
practice of reasoning about each additional decision point helps
subjects integrate mental states of increasing complexity into their
decision-making process. Support for this hypothesis is provided by
studies of children, who learn the orders of theory of mind one by
one. Five-year old children have already had multiple experiences in
daily life with first-order perspective taking. For them,
second-order false belief questions are in the zone of proximal
development. They require exposure to a number of such tasks, in
which they are asked to subsequently answer zero-order, first-order
and second-order questions about a story and to justify their
answers. In this way, they can be trained in second-order perspective
taking (Arslan et al., 2015; Arslan, Taatgen and Verbrugge, 2017).
For adults, second-order ToM in turn-taking games is similarly in
their zone of proximal development: they already solve zero-order and
first-order versions very well. We surmise that Stepwise training
helps them to completely master zero- and first-order ToM in these
games before building on these answers in their second-order
perspective-taking. Like the developmental studies, our training phase
also includes asking subjects to explain what they should have done
and why in case they made a non-optimal decision.
2.4 Scaffold 2: Prompting predictions
The second factor, prompting subjects for predictions, was manipulated
in the first Test Block. Hedden and Zhang (2002) prompted their
subjects to predict Player 2’s decision (in cell B, see Figure 1),
before making their own decision. Thus, subjects were explicitly
asked to take the other player’s perspective, and we hypothesize a priori that these prompts help subjects to actually use
second-order theory of mind attributions such as “the opponent thinks that I intend to stay at C” in their decision-making
process.
We tested this hypothesis in the two Test Blocks of 32 second-order
games each. In the first Test Block, we asked half of the subjects,
randomly assigned to the Prompt group, to predict Player 2’s move
before making their own decision. Subjects assigned to the No-Prompt
group, in contrast, were not explicitly asked to predict Player 2’s
move; they were required only to make their own decision throughout
the experiment. The second Test Block was added to test whether
prompting had long-lasting effects on performance. No subject was
asked to make predictions in the second test block, and performance
differences between the Prompt group and the No-Prompt group would
indicate lasting effects of prompting.
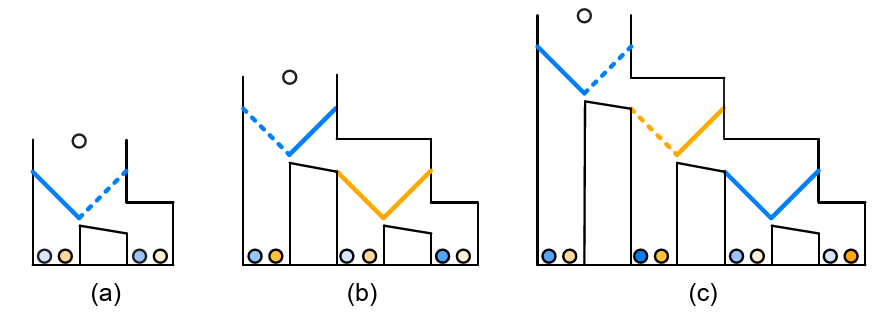
| Figure 5: Examples of zero-order (a), first-order (b), and
second-order (c) Marble Drop games between Player 1 (blue) and
Player 2 (orange). The dashed lines in the figure represent the
optimal decisions. (See Subsection 2.5 for explanation.)
|
2.5 Scaffold 3: Visual Task representation
The third and final factor that we manipulated is the visual task
representation. Before the training phase started, subjects were
randomly assigned to one of two task representations, which did not
change anymore during the remainder of the experiment. One of the
representations was the Matrix Game (Hedden and Zhang, 2002), which is
sometimes criticized for being very abstract and therefore difficult
to understand for subjects (Goodie, Doshi and Young, 2012). We therefore devised a
second representation, henceforth referred to as Marble Drop, which is
similar to the extensive-form game trees so as to clarify the
recursive structure of the decision-making problem by displaying more
intuitively who decides where and what the consequences of each
decision are (Figure 5) (Meijering et al., 2012).
Figure 5 depicts examples of zero-order, first-order, and second-order
Marble Drop games. A white marble is about to drop, and its path can
be manipulated by opening the left or right trapdoor at each decision
point. Player 1’s goal is to let the white marble drop into the bin
containing the darkest possible marble of his/her target color (blue
in these example games), by controlling only the blue
trapdoors. Player 2’s goal is to obtain the darkest possible orange
marble, but Player 2 can only control the orange trapdoors. The
marbles are ranked from light to dark, with darker marbles preferred
over lighter marbles, yielding payoff structures isomorphic to those
in matrix games. Each time, opening the left trapdoor provides access
to a single bin, thus ending the game (“to stay”). Opening the right
trapdoor (“to go”) allows the marble to move to the right to a new
decision point, a pair of trapdoors of the other color, where the
other player decides. The subject is always Player 1, deciding which
of the first pair of trapdoors to open.
For example, in the game of Figure 5, panel (c), Player 1 could reason
as follows: “Suppose I were to open the right blue trapdoor at my
first decision point. Then after that, Player 2 would not open his
right orange trapdoor, because he knows that if he did, I would
then plan to open the left blue final trapdoor, which would give
him the lowest possible payoff, the lightest orange marble. So he
would open the left orange trapdoor, which would in turn give me my
highest possible payoff, the darkest blue marble. So, let me open the
right blue trapdoor at the top.”
We designed the game in such a way that experience with world physics,
in particular with marble runs in childhood, would allow subjects to
easily imagine how the marble would run through a game. Moreover, the
interface of the game was designed to support subjects to quickly see
who could change the path of the marble at which point in the game,
because the trapdoors were color-coded according to who got to decide
where and the target color of that player. Finally, we implemented the
experiments with Marble Drop in such a way that the subjects could see
the marble drop down and, after their initial decision at the first
pair of trapdoors, they could visually follow the marble as it coursed
through the Marble Drop device on the screen.
We hypothesize a priori that the new visual task representation
of Marble Drop provides scaffolding that supports correct use of
second-order theory of mind and thereby leads to better decisions. A
similar approach has been shown to support subjects in learning other
dynamic games, such as Number Scrabble, which is formally equivalent
to the well-known game of Tic-Tac-Toe, whilst subjects perform
significantly better in the latter game
(Michon, 1967; Simon, 1979; Weitzenfeld, 1984).8
Importantly, Marble Drop is game-theoretically isomorphic to Matrix
Games and thus requires essentially the same reasoning (see next
subsection). Instead of using numerical payoffs, as commonly used in
experimental games, we chose colored marbles to counter numerical but
non-optimal reasoning strategies towards goals such as minimizing the
opponent’s outcomes, maximizing the sum of both players’ outcomes, or
maximizing the difference between Player 1 and Player 2 outcomes.
Equivalence of Matrix Game, Marble Drop and extensive form game trees
All three game representations, namely the Matrix Game, Marble Drop
and the classical extensive form game trees, turn out to be
game-theoretically equivalent: the backward induction strategy yields
the same intermediate and final results for them. The three
representations all have terminal nodes, subsequently named A, B, C,
and D. Moreover, the temporal order of play is the same: First, Player
1 decides whether to “stay” and end the game at A or to “move”
further. Then at the second decision point, Player 2 decides whether
to stay and end the game at B or to move further. Finally, at the
third decision point, Player 1 decides whether to stay and end the
game in C or to move and end the game in D.
Finally, the payoff pairs correspond one-to-one between the
representations. For example, the extensive form game tree of Figure
2 has the same payoff structure as the Matrix
Game of Figure 3. The payoff structure of the extensive form game tree
of Figure 1 corresponds to the Marble Drop of
Figure 5 (c), where payoff 1 in the game tree corresponds to the
lightest shade of the corresponding player’s target color, and payoff
4 to the darkest shade.
2.6 Stimuli
Payoffs
The payoffs in Matrix Games are numerical, ranging from 1 to 4,
whereas the payoffs in Marble Drop games are color-graded marbles that
have a one-to-one mapping to the numerical values in the Matrix
Games. The colors of the marbles are four shades of orange and blue,
taken from the HSV (i.e., hue, saturation and value) space. A
sequential color palette is computed by varying saturation, for a
given hue and value. This results in four shades (with saturation from
.2 to 1) for each of the colors orange (hue = .1, value = 1) and blue
(hue = .6, value = 1).
Payoff structures
The payoff structures of the two-person three-stage turn taking games were adapted
from the original game designs of (Hedden and Zhang, 2002).
The payoff structures are selected so that the order of ToM reasoning
mastered by the subjects can be derived from the set of their first
decisions in the experimental games. The total set of payoff
structures, balanced for the number of decisions to continue or stop a
game, is limited to 16 items. These items are listed in Appendix C,
including a detailed discussion of the rationale behind the exclusion
criteria.9
2.7 Procedure
The 43 subjects in the Marble Drop condition were first tested on
color-blindness. They had to be able to distinguish the two colors
blue and orange, and to correctly order the four grades of both orange
and blue in terms of darkness.
To familiarize them with the rules of the sequential games, all
subjects were first presented with a training block that either
consisted of Undifferentiated training or Stepwise training. The
instructions, which appeared on screen, explained how to play the
games and what the goal of each player was. For example, the subjects
in the Stepwise training and Marble Drop condition with orange as
target color received the following instruction about the first-order
training games: “In the next games, there are two sets of
trapdoors. You control the orange trapdoors and the computer controls
the blue trapdoors. The computer is trying to let the white marble end
up in the bin with the darkest blue marble it can get. You still have
to attain the darkest orange marble you can get. Note, the computer
does not play with or against you.” For an example full verbatim
instruction set with illustrations, see Appendix A.
The instructions also mentioned that subjects were playing against a
computer-simulated player. Hedden and Zhang (2002) have shown that
inclusion of a cover story about a purported human opponent did not
affect ToM performance. Each training game was played until either the
subject or the computer-simulated player decided to stop, or until the
last possible decision was made. After each training game, subjects
were presented with accuracy feedback indicating whether the highest
attainable payoff was obtained. In case of an incorrect decision, an
arrow pointed at the cell of the Matrix Game (respectively the bin of
Marble Drop) that contained the highest attainable payoff and the
subject was asked to explain why that cell (or bin) was optimal for
them. Because the feedback never referred to the other player’s mental
states, subjects had to infer these themselves.
The training block was followed by two test blocks, which consisted of
32 second-order games each. As mentioned in Subsection
2.4, the procedure for subjects in the Prompt
and No-Prompt groups differed in the first test block. Subjects in the
Prompt group were first asked to enter a prediction of Player 2’s
decision before they were asked to make a decision at their own first
decision point — between stay-or-go in the Matrix Game, respectively
between opening the left or right trapdoor in Marble Drop. Subjects in
the No-Prompt group, in contrast, were not asked to make
predictions. They were asked only to make decisions. Accuracy feedback
was presented both after entering a prediction and after entering a
decision, but the arrow pointing to the highest attainable payoff was
not shown anymore in the test blocks. The first test block consisted
of 32 trials; each of the 16 payoff structures was presented twice,
but not consecutively. The items were presented in a different random order for each subject. The second test block, also consisting of 32
games, followed the same procedure for all subjects: They were asked
to make their own first decisions only.
3 Results
3.1 Reaction times
Subjects were not instructed regarding the speed of responding: they
were asked only to do the task as well as possible. In the two test
blocks consisting of 32 items each, subjects were confronted with four
occurrences each (in a random order) of the 16 essentially different
games (Table 2, Appendix C). Fortunately, the
reaction time data strongly speak against the possibility of the
subjects having used simple cognitive strategies such as pattern
recognition, because the mean reaction time was still more than 8
seconds (M = 8.5, SE = .61) even in Test Block 2.10
The setup of the prompt condition in Test Block 1 did not allow us to
make a more detailed analysis of the decision times, because the
reaction times of the decisions that subjects in the Prompt group made
after having first made an explicit prediction about the opponent’s
next decision, were expected to be much lower than the bare decisions
of subjects in the No-Prompt group, due to the experimental
design. Moreover, for subjects in the Prompt group, we could not gauge
from their decision times whether their decisions took shorter in Test
Block 2 than in Test Block 1. Therefore, only the accuracy scores are
discussed in the rest of the current study.
3.2 Scaffolding effects
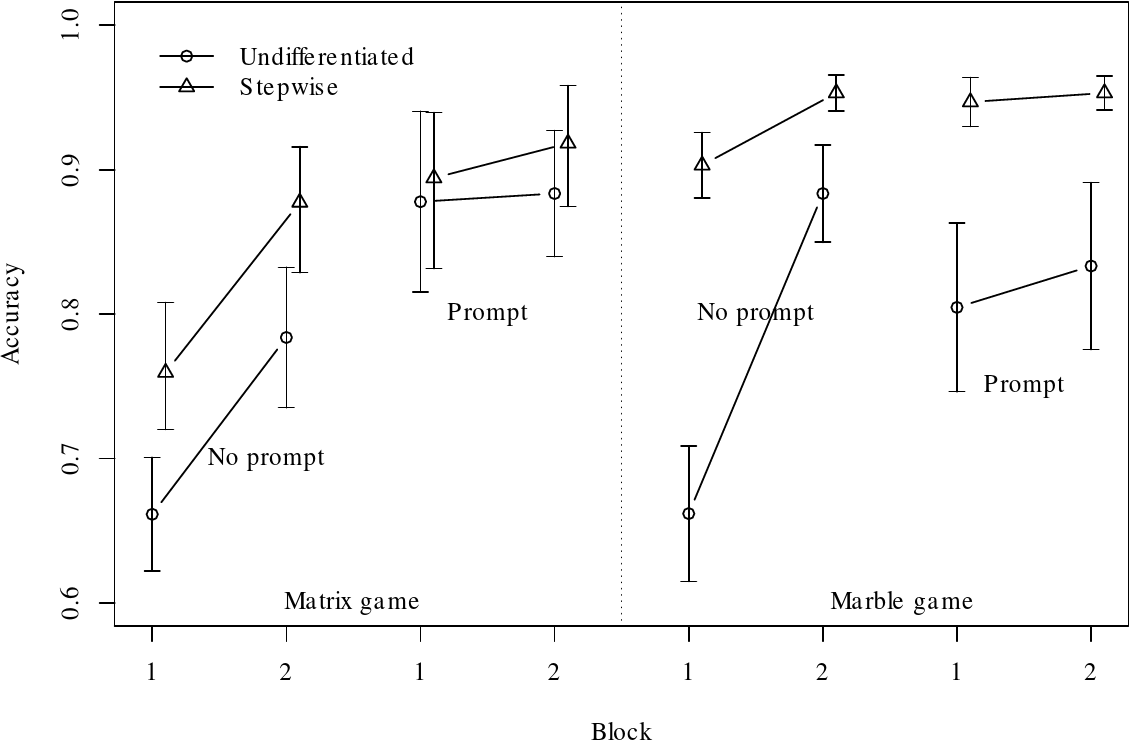
| Figure 6: Accuracy results for all 8 conditions of the experiment for Test Block 1 and Test Block 2. Error bars represent one standard error. |
Figure 6 shows the proportions of accurate predictions for each of the
conditions in the experiment. The data suggest effects of prompting,
training and block, but not necessarily of task representation. To
test the effects of the scaffolding manipulations, we analyzed the
accuracy data of Test Block 1 and Test Block 2 using binomial
mixed-effect models, with subject and problem-ID as random effects
(Baayen, Davidson and Bates, 2008). The training block was excluded from
analysis, because the trials differed between the Stepwise and
Undifferentiated types of training. Because we were interested in the
main effects of our manipulations and the interactions on block, we
first fitted a model with Task representation (Marble Drop or Matrix
Game), Prompt (i.e., prompting or not for predictions about the
opponent’s choice at the second decision point), Training (i.e., the
type of training: Stepwise or Undifferentiated), and Block (i.e., Test
Block 1 or 2) as main effect, and Task representation × Block,
Prompt × Block, Training × Block as interaction
effects.
Analysis of variance indicates main effects of Training (stepwise
better), Prompt, and Block (all with p<.002). The effect of Task
(matrix/marble) was not significant. Figure 6 suggests that
interactions are also present, but most of these could result from
reduction in room for effects to manifest themselves as accuracy
approached the ceiling (and in fact reached it for some subjects in
some conditions).
Of more substantive interest, Prompt had a larger effect in Block 1
than in Block 2 (p<.001 for the interaction overall, and also for
the interaction within each Task); the interaction shows up in Figure
6 as greater slopes (between blocks) for No-prompt than for Prompt. It
is a clear cross-over interaction for the Marble game and this cannot
be explained in terms of compression of the scale. This effect could
be interpreted as a non-lasting effect of Prompt: Prompting subjects
helps them in second-order ToM reasoning by breaking up the reasoning
steps, but after prompting stops, in Test Block 2, the advantage
largely disappears.
3.3 Alternative strategies
One could argue that strictly competitive games — in the sense that
a win for one player is a loss for the other and vice versa — are
easier and more intuitive for people, in contrast to the current game
in which both the subject and the opponent had the self-interested
goal of maximizing their own payoff. Even though the subjects were
carefully instructed about the objective of the game (see verbatim
instructions in Appendix A), it might be that some subjects played
competitively in the sense of maximizing the difference, namely their
own score minus the opponent’s score. Other subjects might have
played cooperatively in the sense of maximizing social welfare, the
sum of their and the opponent’s scores. Therefore, we checked whether
the behavior of a subject was consistent with one of the strategies on
the given items, using a moving average of 11 trials. If the
strategies could not be discriminated based on the responses, the
subject would be assigned to more than one strategy.
As depicted in Figure 7, subjects likely did follow the instructions
to be self-interested by maximizing their own payoff and to assume
that the opponent was self-interested too; especially in the second
half of the experiment, more than 80% could be so classified.
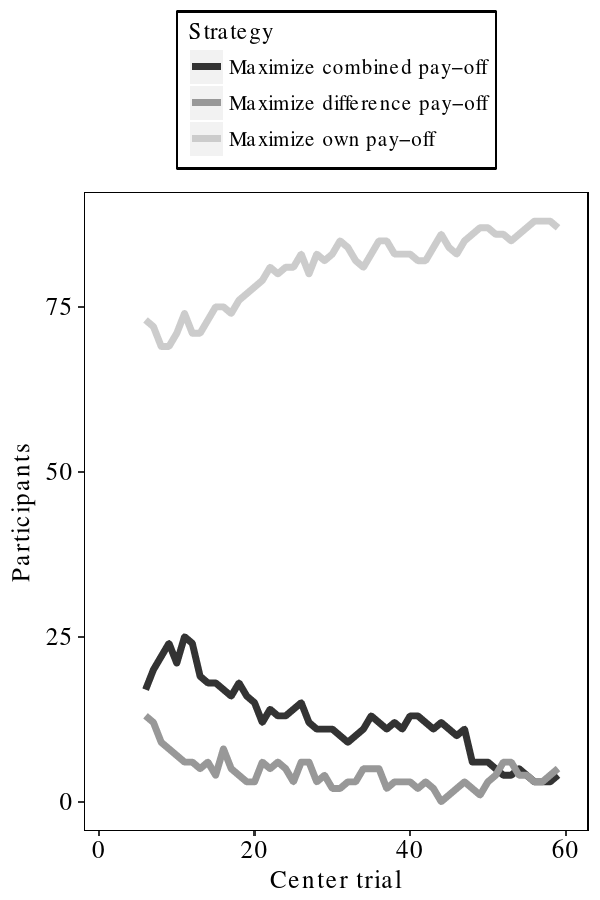
| Figure 7: The y-axis shows the number of subjects that are assigned to a specific strategy. On the x-axis is depicted the center trial of the moving average. The “Maximize own pay-off” corresponds to the task instructions. |
4 General Discussion
The main aim of our experiment was to find out how we can best support
adults in the perspective taking needed to make optimal decisions in a
three-step two-player game. We chose three manipulations for which we
had reason to believe that they would help scaffold subjects’
second-order theory of mind, namely 1) Stepwise training, 2) Prompting
subjects to make an explicit prediction of the opponent’s next choice
(that included the opponent’s taking the subject’s final choice into
account) and 3) a less abstract, easier to understand visual task
representation, namely Marble Drop.
Subjects clearly benefit from a carefully constructed Stepwise
training regime, in which they are first asked to make decisions in a
few one-choice versions that introduce the goal and the game
representation but do not require any reasoning about an opponent,
then a few two-choice versions in which subjects have to use
first-order theory of mind to predict the opponent’s next (simple)
choice between two end-points, and finally a few three-choice versions
for which second-order theory of mind is required. Their accuracy is
much higher than for the other half of the subjects, who had gone
through a training regime in which all training games were
three-choice games with payoffs distributed in such a way that the
third choice made no difference for the optimal first and second
decisions. For such so-called trivial games in this Undifferentiated
training regime, first-order theory of mind was always sufficient.
Prompting subjects to think about the opponent’s perspective at the
next decision point helps them in making their own optimal decision at
the first decision point of the current game. In particular, when
explicitly prompted, subjects tend to give correct
predictions. However, prompting improves performance mainly in the
session in which it is applied, and does not have much lasting effect
on the subsequent session without prompts.
Finally, it appears that the Task representation does not really
matter: Subjects achieve about the same accuracy scores in the Marble
Drop representation as in the more abstract Matrix Game. This
surprised us for several reasons. Firstly, we had carefully designed
Marble Drop to be easy to understand and to fit with people’s
experience as children with games in which marbles drop and slide down
devices, partly under control of the child. Secondly, the
decision-making literature abounds with examples in which a proper
visual representation improves people’s accuracy. Finally, several
subjects told us in the debriefing how insightful they had found
Marble Drop. Apparently, the less abstract visual representation of
Marble Drop is not sufficient to support subjects to take the
second-order perspective required to make optimal decisions.
4.1 Errors of rationality and theory of mind
Zhang and colleagues argue that, for people to make an optimal first
decision in three-move two-player Matrix Games, they need two
different capacities: a) perspective taking by recursive theory of
mind, to make a correct mental model of their opponent and predict his
next decision and b) instrumental rationality, to make an optimal
first decision of their own, based both on their mental model of the
opponent and an analysis of relevant payoffs. Thus, instrumental
rationality errors are made when subjects are not engaged in “fully
enacting the possible consequences of their opponent’s action and
making contingency plans based on these predicted consequences”
(Hedden and Zhang, 2002; Jones and Zhang, 2003; Zhang, Hedden and Chia, 2012).
4.1.1 Rationality errors
In the Prompt group in Test Block 1, a number of subjects fail to
conclude from their correct prediction what their own optimal decision
should be. Sometimes subjects make the opposite error: They first make
an incorrect prediction about the opponent’s next step, but do not to
take it into account when making their own, optimal, decision at the
first decision point. We follow Hedden and Zhang (2002) in calling
both types of mismatch rationality errors. Subjects in the
Prompt group made rationality errors in 12.6% of trials in the
relevant Test Block 1.
If we look more closely at the total number of 191 (out of 1504)
trials in our experiment in which a subject made a rationality error
— trials with a correct decision but a wrong prediction and vice
versa — we see that subjects in those trials tend to end the game by
staying in cell A in the Matrix Game or let the marble drop into the
leftmost bin of Marble Drop so as to receive the first possible
pay-off (n = 122) instead of giving the opponent a chance to play (n =
69).11 This asymmetry is striking, considering that the numbers of
times a subject should stay or go according to the optimal solution
prescribed by game theory, had been balanced throughout the experiment
(Table 2, Appendix C). This finding indicates that
a majority, around 2/3 of subjects, use a risk-averse strategy when
making a rationality error.
In contrast, in the studies of Zhang and colleagues this “stay in
cell A” type of rationality error occurred equally often as the
“move to cell B” type. Because all the trials in our test blocks are
diagnostic for second-order ToM, the pay-off for the player was 3 for
the first cell/bin in all such trials in which they “played
safe”.12 These subjects would forego an attainable maximal payoff of
4 at a later stage of the game (see lines 9–16 of Table
2, Appendix C). However, this type of rationality
error is rationalizable: The subjects could be sure of gaining 3
points when staying at A, while they ran the risk of gaining only 1 or
2 points if the opponent were to unexpectedly decide differently from
their predicted rational decision. In these cases, subjects were not
absolutely certain that the opponent would act according to their
prediction and preferred to keep matters in their own hands.
There are also important similarities between our experiment and Zhang
and colleagues’ in terms of rationality errors. Zhang, Hedden and Chia (2012) make
a comparison of the ratios of rationality errors in cases in which
subjects need only first-order theory of mind in cell B when making
their own decision in the role of Player 2, versus cases in which
subjects in the role of Player 1 need to make a prediction about their
opponent Player 2’s decision in cell B, requiring second-order theory
of mind. Interestingly, the ratios of rationality errors that subjects
make are almost the same, whether they need to use first-order or
second-order theory of mind, and rather low in both cases: decreasing
from around 1/5 in the beginning of the 64 test games down to around
1/10 at the end (Zhang, Hedden and Chia, 2012). Similarly, in our experiment,
rationality errors occurred only around 1/8 of items in Test Block 1.
Therefore, both Zhang, Hedden and Chia and our current study
corroborate the earlier results of Hedden and Zhang: The ratios of
rationality errors do not significantly differ between the condition
in which subjects play standard Matrix Games against a myopic
(zero-order ToM) opponent or against a predictive (first-order ToM)
opponent (Hedden and Zhang, 2002). Thus, all these studies support the
conclusion that instrumental rationality (making your own decision on
the basis of your prediction of the opponent’s next decision) is
distinct from and apparently easier for subjects than the perspective
taking required to make a correct mental model of the opponent,
requiring second-order theory of mind (Jones and Zhang, 2003).
4.1.2 Errors in recursive perspective taking
In the current experiment, the non-optimal decisions that subjects
make are mostly due to difficulties in making a correct model of the
opponent. Because we usually did not ask subjects for explicit
predictions (only the Prompt group in the Test Block 1), we have to
gauge their predictions from their decisions and we cannot provide an
analysis of perspective-taking errors in their predictions. However,
the patterns of decisions per subject indicate that it was clear to
them that the opponent’s goal, like the subject’s own, was to
self-interestedly maximize their own payoff; they did not think, for
example, that the goal was to maximize the joint payoff or to maximize
the difference between the players’ payoffs (see Subsection
3.3).
Our previous cognitive modeling work on Marble Drop indicates that
adults, different from children, do take the opponent’s goals into
account. However, when subjects make non-optimal decisions, their
decision patterns over all payoff structures often fit with having a
too simple model of the opponent, using only first-order theory of
mind. For example, they expect the opponent to always play safe by
staying at B if either of their payoffs in C or D is smaller than the
one in B, or to always take a risk by moving on if either of their
payoffs in C or D is larger than the one in B. Both these simple
models do not take into account that the opponent is also reasoning
about the subject’s final decision. Based on feedback, many subjects
improve their model of the opponent in the course of the experiment
and start to correctly make a second-order theory of mind
model. Starting out “as simple as possible”, they learn to reason
“as complex as necessary” (Meijering et al., 2014).
4.2 How do subjects reason when they make optimal decisions?
We surmise that subjects who make optimal decisions do not apply a
fixed simple reasoning strategy based on comparison of payoffs only,
such as backward induction, without explicitly reasoning about mental
states.13 Our attribution of recursive perspective
taking to subjects who make optimal decisions is corroborated by a
related Marble Drop experiment, in which subjects were also told that
they were playing against a self-interested computer opponent
(Meijering et al., 2012). Subjects’ eye movements show them not to use
backward induction. They attend mostly to the trapdoors, the decision
points, not only to the payoff pairs, which would have been sufficient
for backward induction.
Subjects’ eye movements first show predominantly left-to-right
progressions and only then, for the more difficult payoff structures,
their eyes make right-to-left progressions at the end of reasoning
about a game. This fits what we dub the “forward reasoning plus
backtracking” reasoning strategy: you start at the first decision
point in a game and proceed to the next one for as long as higher
outcomes are expected to be available at future decision points; when
you discover that you may have unknowingly skipped the highest
attainable outcome at a previous decision point, you jump back to
inspect whether that outcome is indeed attainable
(Meijering et al., 2012).
This temporal order of subjects’ reasoning is suggestive of causal
reasoning, which they have learnt from early childhood
(Gopnik et al., 2004): First “What would happen if I chose to move on to
the right?”, then “What would happen if the opponent then chose to
move on to the right as well?”, and finally “What would I then
choose at the final pair of trapdoors? Oh, that would give my opponent
the lightest-colored blue marble, so he probably wouldn’t want to let
me have the final choice and end up there.”
Moreover, when we compare the reaction times with computational models
of backward induction and of forward reasoning plus backtracking, it
turns out that subjects’ patterns of decision times on all game items
fit “forward reasoning plus backtracking” much better than backward
induction (Bergwerff et al., 2014).14 Evidence for such forward
reasoning has also been found in some other turn-taking games, such as
sequential bargaining and a sequential version of the trust game
(Johnson et al., 2002; Evans and Krueger, 2011).
4.3 Comparison with another study supporting second-order perspective-taking
Goodie, Doshi and Young (2012) claim that perspective taking by itself
is not the bottleneck in turn-taking games requiring
second-order theory of mind. In line with this, they propose
two ways to support people in applying second-order ToM in a
turn-taking game such as the Matrix game. Their first manipulation is
to turn the abstract Matrix Game into a game-theoretically isomorphic
version that has a concrete military cover story; this turns out to
have no effect. Their second manipulation is to transform the Matrix
Game into a competitive fixed-sum game with a single pay-off shown per
cell. They argue that in these zero-sum games, adults are perfectly
able to apply second-order ToM against a predictive player, with more
than 90% correct decisions (Goodie, Doshi and Young, 2012). They argue that such
strictly competitive games are more natural for people (as also
claimed by (Bornstein, Gneezy and Nagel, 2002)).
However, at second sight, there is an alternative explanation for
their positive findings about the zero-sum game. In their Experiments
1 and 2, all 40 critical trials of their 80-trial test phase displayed
the same ordering of payoffs over the four subsequent leaves of the
centipede-like decision tree, namely 3–2–1–4; these had been mapped
to probabilities with different cardinalities, but in the same order
(Goodie, Doshi and Young, 2012). This similarity between items may have enabled
their subjects after a number of trials to understand that the solutions
all followed the same pattern (similar to our game 3 of Table
2 of Appendix C). The successive three optimal
choices are always the same for the zero-sum games: Player 1 stays at
A, because Player 2 stays at B, because Player 1 goes on to D.
In our experiment, such pattern recognition could not arise because
each subject encountered only 4 spaced instances of each of the 16
payoff structures, and all these 16 of our payoff structures were
essentially different (see Table 2 of Appendix C).
Also, in real life, many important social situations requiring
second-order ToM cannot be re-cast as zero-sum games, but only as
general-sum games, so the Matrix Game or Marble Drop appear to be
better ways to train people in second-order perspective taking for
real-life intelligent interactions.
4.4 Implications: De-biasing decision makers
The findings of the current study, in particular the notion of
scaffolding decision making for subjects by stepwise training, could
also be of interest in attempting to reduce the biases of decision
makers in other social situations. For example, people often allocate
resources in a parochial way. Without explicitly wanting to harm
out-groups, people reduce their own earnings in order to support their
own in-group (e.g., their nation), even if their decision is so
detrimental to an out-group (e.g., another nation) that the overall
outcome of their decision is negative, while it could have been
positive (Bornstein and Ben-Yossef, 1994; Baron, Ritov and Greene, 2013). One way to reduce this type
of in-group bias is to change the task representation by asking
subjects to compute all gains and losses (Baron, 2001). In view of the results of the current study, it might
alternatively be helpful to offer the subjects a stepwise training in
which they have to make allocation decisions of increasing complexity
and with growing numbers of parties. After each non-optimal allocation
decision in the stepwise training block, subjects could be shown which
other decision would have had a more positive overall outcome and they
could be asked to explain why that alternative decision is better. It
would be interesting to compare the effects of these two de-biasing
methods, asking for explicit computations and stepwise training, in a
future experiment.
A related phenomenon is the bias towards self payoffs in sequential
trust games, where people appear not to be sufficiently interested in
perspective-taking to even gather information about the opponents’
payoffs, often to their own detriment (Evans and Krueger, 2014). Another type
of bias is the false consensus phenomenon, in which people think that
their own judgments and decisions are more prevalent in their
community than is actually the case (Ross, Greene and House, 1977). Related to this,
the “Isn’t everyone like me?” bias occurs in a normal form game in
which subjects who choose one action ego-centrically tend to believe
that other players will choose that same action in a larger proportion
than is expected by subjects who choose the other action
(Rubinstein and Salant, 2016). It would be interesting to investigate whether
these biases can also be alleviated by step-by-step training in
properly taking other people’s perspectives into account.
4.5 Conclusion
In two-player turn-taking games with three decision points, reasoning
about someone else’s decision that in turn depends on your own plan is
difficult, even for adults. The required second-order perspective
taking (“the opponent thinks that I would intend to go left at the
last decision point”) does not appear to happen automatically or
spontaneously. However, our results have shown that subjects in such
turn-taking games can learn to take the required perspective to make
optimal decisions when they are knowingly playing against a
self-interested opponent taking the subject’s goal into account.
From a theoretical perspective, it would seem that subjects could be
supported by three manipulations, separately or in combination: 1)
step-wise training, in which they are subsequently trained to make and
explain decisions in games with one, two and three decision point that
require zero-order, first-order and second-order theory of mind,
respectively; 2) prompting subjects to predict what the opponent would
choose at the next decision point before making their own decision at
the first decision point; and 3) using an intuitive visual
interpretation, namely Marble Drop, which is closer to people’s daily
experiences than the Matrix Game.
It turns out that, while prompting for predictions has largely a
short-time effect and the visual task presentation does not make much
of a difference, there is a clear positive main effect of stepwise
training. Thus, stepwise training can be used to teach people to
recursively put themselves in other people’s shoes, which is important
in many social interactions, from the simple turn-taking Matrix Game
to international peace negotiations.
References
-
-
Arslan, B., Hohenberger, A., and Verbrugge, R. (2017a).
Syntactic recursion facilitates and working memory predicts recursive
theory of mind.
PloS one, 12(1):e0169510.
[ bib ]
-
-
Arslan, B., Taatgen, N. A., and Verbrugge, R. (2017b).
Five-year-olds' systematic errors in second-order false belief tasks
are due to first-order theory of mind strategy selection: A computational
modeling study.
Frontiers in Psychology, 8.
[ bib ]
-
-
Arslan, B., Verbrugge, R., Taatgen, N., and Hollebrandse, B. (2015).
Teaching children to attribute second-order false beliefs: A training
study with feedback.
In Proceedings of the 37th Annual Conference of the Cognitive
Science Society, pages 108--113.
[ bib ]
-
-
Baayen, R. H., Davidson, D. J., and Bates, D. M. (2008).
Mixed-effects modeling with crossed random effects for subjects and
items.
Journal of Memory and Language, 59(4):390--412.
[ bib ]
-
-
Baron, J. (2001).
Confusion of group interest and self-interest in parochial
cooperation on behalf of a group.
Journal of Conflict Resolution, 45(3):283--296.
[ bib ]
-
-
Baron, J., Ritov, I., and Greene, J. D. (2013).
The duty to support nationalistic policies.
Journal of Behavioral Decision Making, 26(2):128--138.
[ bib ]
-
-
Baron-Cohen, S., Jolliffe, T., Mortimore, C., and Robertson, M. (1997).
Another advanced test of theory of mind: Evidence from very high
functioning adults with autism or Asperger syndrome.
Journal of Child Psychology and Psychiatry, 38(7):813--822.
[ bib ]
-
-
Bergwerff, G., Meijering, B., Szymanik, J., Verbrugge, R., and Wierda, S.
(2014).
Computational and algorithmic models of strategies in turn-based
games.
In Proceedings of the 36th Annual Conference of the Cognitive
Science Society, pages 1778--1783.
[ bib ]
-
-
Bhatt, M. and Camerer, C. F. (2005).
Self-referential thinking and equilibrium as states of mind in games:
fMRI evidence.
Games and Economic Behavior, 52(2):424--459.
[ bib ]
-
-
Bicchieri, C. (1989).
Self-refuting theories of strategic interaction: A paradox of common
knowledge.
Erkenntnis, pages 69--85.
[ bib ]
-
-
Bornstein, G. and Ben-Yossef, M. (1994).
Cooperation in intergroup and single-group social dilemmas.
Journal of Experimental Social Psychology, 30(1):52--67.
[ bib ]
-
-
Bornstein, G., Gneezy, U., and Nagel, R. (2002).
The effect of intergroup competition on group coordination: An
experimental study.
Games and Economic Behavior, 41(1):1--25.
[ bib ]
-
-
Camerer, C. F., Ho, T.-H., and Chong, J. K. (2015).
A psychological approach to strategic thinking in games.
Current Opinion in Behavioral Sciences, 3:157--162.
[ bib ]
-
-
Clark, A. (1997).
Economic reason: The interplay of individual learning and external
structure.
In Drobak, J., editor, The Frontiers of the New Institutional
Economics, pages 269--290. Academic Press.
[ bib ]
-
-
Colman, A. M. (2003).
Cooperation, psychological game theory, and limitations of
rationality in social interaction.
Behavioral and Brain Sciences, 26(2):139--153.
[ bib ]
-
-
Dambacher, M., Haffke, P., Groß, D., and Hübner, R. (2016).
Graphs versus numbers: How information format affects risk aversion
in gambling.
Judgment and Decision Making, 11(3):223--242.
[ bib ]
-
-
Devaine, M., Hollard, G., and Daunizeau, J. (2014a).
The social Bayesian brain: Does mentalizing make a difference when
we learn?
PLoS Computational Biology, 10(12):e1003992.
[ bib ]
-
-
Devaine, M., Hollard, G., and Daunizeau, J. (2014b).
Theory of mind: Did evolution fool us?
PloS ONE, 9(2):e87619.
[ bib |
DOI ]
-
-
Evans, A. M. and Krueger, J. I. (2011).
Elements of trust: Risk and perspective-taking.
Journal of Experimental Social Psychology, 47(1):171--177.
[ bib ]
-
-
Evans, A. M. and Krueger, J. I. (2014).
Outcomes and expectations in dilemmas of trust.
Judgment and Decision Making, 9(2):90--103.
[ bib ]
-
-
Fernyhough, C. (2008).
Getting Vygotskian about theory of mind: Mediation, dialogue, and
the development of social understanding.
Developmental Review, 28(2):225--262.
[ bib ]
-
-
Filippova, E. and Astington, J. W. (2008).
Further development in social reasoning revealed in discourse irony
understanding.
Child Development, 79(1):126--138.
[ bib ]
-
-
Flobbe, L., Verbrugge, R., Hendriks, P., and Krämer, I. (2008).
Children's application of theory of mind in reasoning and language.
Journal of Logic, Language and Information, 17:417--442.
[ bib ]
-
-
Frey, S. and Goldstone, R. L. (2013).
Cyclic game dynamics driven by iterated reasoning.
PloS ONE, 8(2):e56416.
[ bib |
DOI ]
-
-
Ghosh, S., Heifetz, A., Verbrugge, R., and de Weerd, H. (2017).
What drives people's choices in turn-taking games, if not
game-theoretic rationality?
In Lang, J., editor, Proceedings of the 16th Conference on
Theoretical Aspects of Rationality and Knowledge (TARK 2017),
volume EPTCS 251 of EPTCS, pages 265--284.
[ bib ]
-
-
Goodie, A. S., Doshi, P., and Young, D. L. (2012).
Levels of theory-of-mind reasoning in competitive games.
Journal of Behavioral Decision Making, 25(1):95--108.
[ bib ]
-
-
Gopnik, A., Glymour, C., Sobel, D. M., Schulz, L. E., Kushnir, T., and Danks,
D. (2004).
A theory of causal learning in children: Causal maps and Bayes
nets.
Psychological Review, 111(1):3--32.
[ bib ]
-
-
Happé, F. G. (1995).
The role of age and verbal ability in the theory of mind task
performance of subjects with autism.
Child Development, 66(3):843--855.
[ bib ]
-
-
Hedden, T. and Zhang, J. (2002).
What do you think I think you think? Strategic reasoning in
matrix games.
Cognition, 85(1):1--36.
[ bib ]
-
-
Ho, T.-H. and Su, X. (2013).
A dynamic level-k model in sequential games.
Management Science, 59(2):452--469.
[ bib ]
-
-
Hsu, Y. K. and Cheung, H. (2013).
Two mentalizing capacities and the understanding of two types of lie
telling in children.
Developmental Psychology, 49(9):1650--1659.
[ bib ]
-
-
Johnson, E., Camerer, C., Sen, S., and Rymon, T. (2002).
Detecting failures of backward induction: Monitoring information
search in sequential bargaining.
Journal of Economic Theory, 104(1):16--47.
[ bib ]
-
-
Jones, M. and Zhang, J. (2003).
Which is to blame: Instrumental rationality, or common knowledge?
Behavioral and Brain Sciences, 26(02):166--167.
Commentary on Colman, 2003.
[ bib ]
-
-
Kawagoe, T. and Takizawa, H. (2012).
Level-k analysis of experimental centipede games.
Journal of Economic Behavior and Organization, 82(2):548--566.
[ bib ]
-
-
Kieslich, P. J. and Hilbig, B. E. (2014).
Cognitive conflict in social dilemmas: An analysis of response
dynamics.
Judgment and Decision Making, 9(6):510.
[ bib ]
-
-
Kinderman, P., Dunbar, R., and Bentall, R. P. (1998).
Theory-of-mind deficits and causal attributions.
British Journal of Psychology, 89(2):191--204.
[ bib ]
-
-
Kuijper, S. J., Hartman, C. A., Bogaerds-Hazenberg, S., and Hendriks, P.
(2017).
Narrative production in children with autism spectrum disorder
(ASD) and children with attention-deficit/hyperactivity disorder (ADHD):
Similarities and differences.
Journal of Abnormal Psychology, 126(1):63--75.
[ bib ]
-
-
Li, J., Liu, X.-P., and Zhu, L. (2011).
Flexibility of theory of mind in a matrix game when partner's level
is different.
Psychological Reports, 109(2):675--685.
[ bib ]
-
-
Lin, S., Keysar, B., and Epley, N. (2010).
Reflexively mindblind: Using theory of mind to interpret behavior
requires effortful attention.
Journal of Experimental Social Psychology, 46(3):551--556.
[ bib ]
-
-
Mata, A. and Almeida, T. (2014).
Using metacognitive cues to infer others' thinking.
Judgment and Decision Making, 9(4):349--359.
[ bib ]
-
-
McKelvey, R. D. and Palfrey, T. R. (1992).
An experimental study of the centipede game.
Econometrica: Journal of the Econometric Society, pages
803--836.
[ bib ]
-
-
Mehlhorn, K., Taatgen, N. A., Lebiere, C., and Krems, J. F. (2011).
Memory activation and the availability of explanations in sequential
diagnostic reasoning.
Journal of Experimental Psychology: Learning, Memory, and
Cognition, 37(6):1391--1411.
[ bib ]
-
-
Meijering, B., Taatgen, N. A. ., van Rijn, H., and Verbrugge, R. (2014).
Modeling inference of mental states: As simple as possible, as
complex as necessary.
Interaction Studies, 15(3):455--477.
[ bib ]
-
-
Meijering, B., van Rijn, H., Taatgen, N., and Verbrugge, R. (2012).
What eye movements can tell about theory of mind in a strategic game.
PloS ONE, 7(9):e45961.
[ bib ]
-
-
Michon, J. A. (1967).
The game of JAM--an isomorph of Tic-Tac-Toe.
American Journal of Psychology, 80(1):137--140.
[ bib ]
-
-
Nagel, R. (1995).
Unraveling in guessing games: An experimental study.
The American Economic Review, 85(5):1313--1326.
[ bib ]
-
-
Nagel, R. and Tang, F. F. (1998).
Experimental results on the centipede game in normal form: An
investigation on learning.
Journal of Mathematical Psychology, 42(2):356--384.
[ bib ]
-
-
Oakman, J. (2002).
The Camp David Accords: A case study on international
negotiation.
Technical report, Princeton University, Woodrow Wilson School of
Public and International Affairs.
[ bib ]
-
-
Osborne, M. J. and Rubinstein, A. (1994).
A Course in Game Theory.
MIT Press.
[ bib ]
-
-
Perner, J. and Wimmer, H. (1985).
“John thinks that Mary thinks that ...": Attribution of
second-order beliefs by 5- to 10-year old children.
Journal of Experimental Child Psychology, 5:125--137.
[ bib ]
-
-
Premack, D. and Woodruff, G. (1978).
Does the chimpanzee have a theory of mind?
Behavioral and Brain Sciences, 4:515--526.
[ bib ]
-
-
Raijmakers, M., Mandell, D., van Es, S., and Counihan, M. (2014).
Children's strategy use when playing strategic games.
Synthese, 191(3):355--370.
[ bib ]
-
-
Rosenthal, R. (1981).
Games of perfect information, predatory pricing, and the chain store.
Journal of Economic Theory, 25(1):92--100.
[ bib ]
-
-
Ross, L., Greene, D., and House, P. (1977).
The `false consensus effect': An egocentric bias in social perception
and attribution processes.
Journal of Experimental Social Psychology, 13(3):279--301.
[ bib ]
-
-
Rubinstein, A. (2013).
Response time and decision making: An experimental study.
Judgment and Decision Making, 8(5):540--551.
[ bib ]
-
-
Rubinstein, A. and Salant, Y. (2016).
“Isn't everyone like me?” On the presence of self-similarity in
strategic interactions.
Judgment and Decision Making, 11(2):168--173.
[ bib ]
-
-
Simon, H. (1979).
Information processing models of cognition.
Annual Review of Psychology, 30(1):363--396.
[ bib ]
-
-
Sullivan, K., Zaitchik, D., and Tager-Flusberg, H. (1994).
Preschoolers can attribute second-order beliefs.
Developmental Psychology, 30(3):395--402.
[ bib ]
-
-
Talwar, V., Gordon, H. M., and Lee, K. (2007).
Lying in the elementary school years: Verbal deception and its
relation to second-order belief understanding.
Developmental Psychology, 43(3):804--810.
[ bib ]
-
-
Telhami, S. (1992).
Evaluating bargaining performance: The case of Camp David.
Political Science Quarterly, 107(4):629--653.
[ bib ]
-
-
Verbrugge, R. (2009).
Logic and social cognition: The facts matter, and so do computational
models.
Journal of Philosophical Logic, 38(6):649--680.
[ bib ]
-
-
Vygotsky, L. (1987).
Thinking and speech.
In Rieber, R. W. and Carton, A. S., editors, The Collected Works
of L. S . Vygotsky: Problems of General Psychology. Plenum Press.
Original publication in Russian 1934.
[ bib ]
-
-
Weerd, H. d., Diepgrond, D., and Verbrugge, R. (2017a).
Estimating the use of higher-order theory of mind using computational
agents.
The B.E. Journal of Theoretical Economics.
[ bib ]
-
-
Weerd, H. d., Verbrugge, R., and Verheij, B. (2013).
How much does it help to know what she knows you know? An
agent-based simulation study.
Artificial Intelligence, 199:67--92.
[ bib |
DOI ]
-
-
Weerd, H. d., Verbrugge, R., and Verheij, B. (2017b).
Negotiating with other minds: The role of recursive theory of mind in
negotiation with incomplete information.
Autonomous Agents and Multi-Agent Systems, 31(2):250--287.
[ bib |
DOI ]
-
-
Weitzenfeld, J. S. (1984).
Valid reasoning by analogy.
Philosophy of Science, 51(1):137--149.
[ bib ]
-
-
Wellman, H. M., Cross, D., and Watson, J. (2001).
Meta-analysis of theory-of-mind development: The truth about false
belief.
Child Development, 72(3):655--684.
[ bib ]
-
-
Wimmer, H. and Perner, J. (1983).
Beliefs about beliefs: Representation and constraining function of
wrong beliefs in young children's understanding of deception.
Cognition, 13:103--128.
[ bib ]
-
-
Wood, D., Bruner, J. S., and Ross, G. (1976).
The role of tutoring in problem solving.
Journal of Child Psychology and Psychiatry, 17(2):89--100.
[ bib ]
-
-
Zhang, J., Hedden, T., and Chia, A. (2012).
Perspective-taking and depth of theory-of-mind reasoning in
sequential-move games.
Cognitive Science, 36(3):560--573.
[ bib ]
This file was generated by
bibtex2html 1.98.
Appendix A: Instructions
Here follows a sample set of instructions as presented verbatim to subjects, all of them given in the form for the Marble Drop task representation. First we present the instructions for Stepwise training, then the instructions for the test blocks for the Prompting group. The instructions for other conditions are similar.
Instructions for Step-wise training
The subjects first received the instructions for zero-order games on the screen, after which they practiced four zero-order games. Then they were shown the instructions for first-order games, after which they practiced eight different first-order games. Finally, they received the instructions for the second-order games on the screen, after which they went through eight second-order practice games.
Instructions zero-order games
In this task, you will be playing marble games such as the one in the figure below.
A white marble is about to drop and you can change its path by removing one of two orange trapdoors. The white marble has to end up in the bin with the darkest orange marble.
Press \ to remove the left trapdoor, and / to remove the right trapdoor.
Press spacebar to begin.
Instructions first-order games
In the next games, there are two sets of trapdoors. You control the orange trapdoors and the computer controls the blue trapdoors. The computer is trying to let the white marble end up in the bin with the darkest blue marble it can get. You still have to attain the darkest orange marble you can get. Note, the computer does not play with or against you.
Press spacebar to begin.
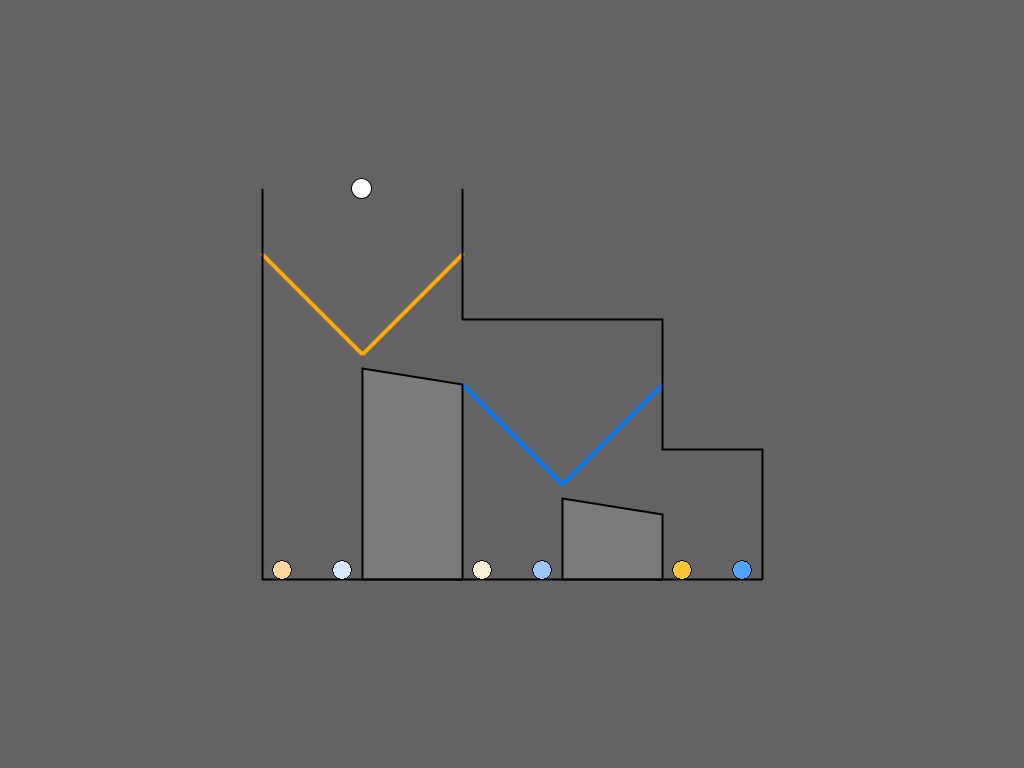
Instructions second-order games
In the next games, there are three sets of trapdoors. Again, you control the orange trapdoors, and the computer controls the blue trapdoors.
Note, for its decision, the computer takes into account what your choice will be at the third set of trapdoors. Remember, the computer does not play with or against you.
Good luck! Press spacebar to begin.
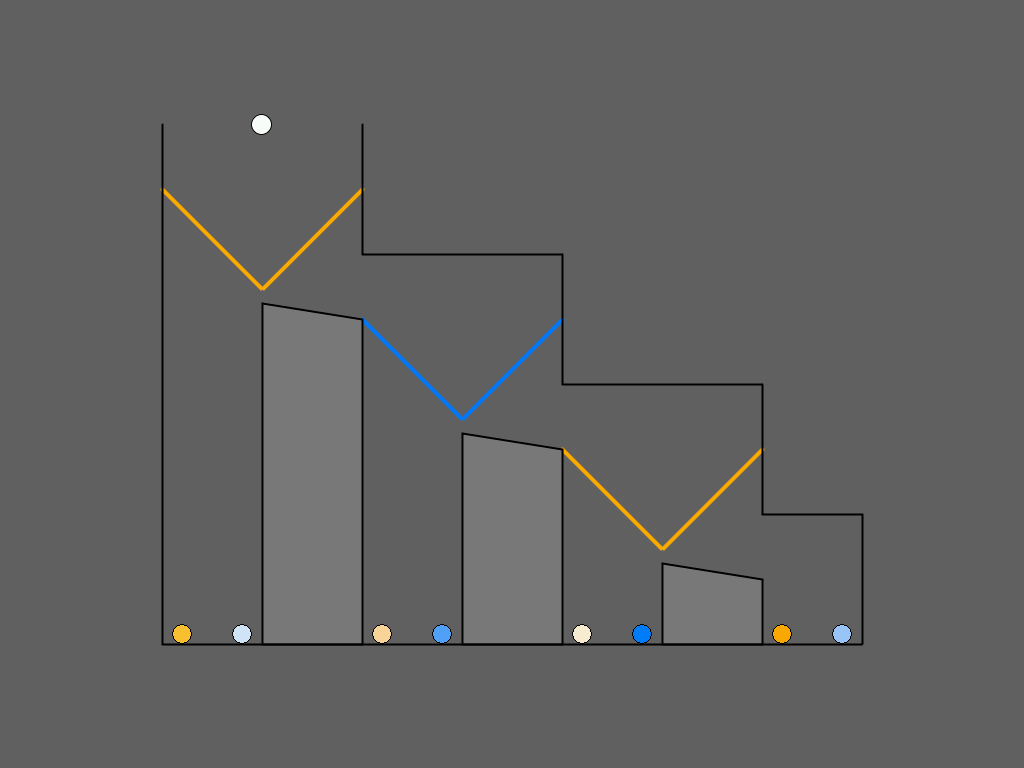
Instructions at the start of the Test Blocks
After the training items, the subjects were shown new instructions at the start of the first and the second Test Block. Below, we present the instructions at the beginning of Test Block 1 and Test Block 2 for the Prompt group.
Instructions second-order prediction-decision games: Test Block 1
The next games are slightly different. First, you have to predict what the computer will do at the second set of trapdoors.
Secondly, you have to decide what to do at the first set of trapdoors.
To speed up the experiment, the animations are removed from the games.
Good luck! Press spacebar to begin.
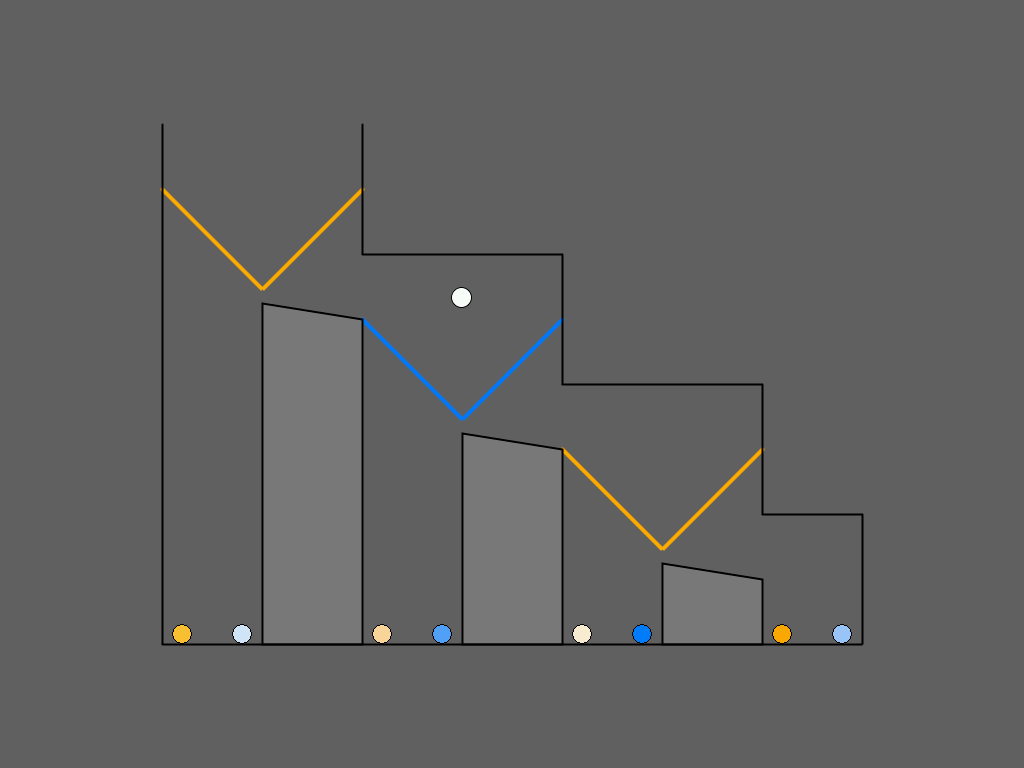
Instructions second-order prediction-decision games: Test Block 2
In the next games, you do not have to predict anymore what the computer will do at the second set of trapdoors.
You immediately receive feedback after you have decided what to do at the first set of trapdoors.
Good luck!
Press spacebar to begin.
Appendix B: the 2 × 2 × 2 groups and allocation of subjects
Altogether, there were 93 subjects. Per manipulation, here are the totals of subjects:
-
Training: Stepwise training 46, Undifferentiated training 47;
- Prompting for predictions: Prompt 47, No-Prompt 46;
- Task representation: 43 Marble Drop, 50 Matrix Game.
Table 1 gives the numbers of subjects per group.
| Table 1: The 2 x 2 x 2 experimental groups and numbers of subjects for each |
group nr. | Training | Prompting | Task Representation | number of subjects |
1 | Stepwise | Prompt | Marble Drop | 10 |
2 | Stepwise | Prompt | Matrix Game | 13 |
3 | Stepwise | No-Prompt | Marble Drop | 10 |
4 | Stepwise | No-Prompt | Matrix Game | 13 |
5 | Undifferentiated | Prompt | Marble Drop | 12 |
6 | Undifferentiated | Prompt | Matrix Game | 12 |
7 | Undifferentiated | No-Prompt | Marble Drop | 11 |
8 | Undifferentiated | No-Prompt | Matrix Game | 12 |
Appendix C: Pay-off structures
Tables 2, 3, 4, and 5
represent the relevant payoff structures, together with corresponding correct decisions and predictions for our experiment.
Letters A, B, C and D stand for the bins in the Marble Drop game from left to right, respectively for subsequent cells in the Matrix game. Each payoff pair represents the payoffs of Player 1 and Player 2, respectively, where 1 represents the lowest payoff (corresponding to the lightest shade of their target color in Marble Drop), while 4 represents the highest payoff (corresponding to the darkest shade of their target color in Marble Drop).
Second-order payoff structures for games with three decision points
The following computation has been adapted from Section 2.1.2 of (Hedden and Zhang, 2002).
In principle, there are 24 × 24 = 576 different payoff structures for three-decision Matrix and Marble Drop games, on the basis of dividing pairs of payoffs from 1, 2, 3, 4 for both players over four cells. However, by far not all of these 576 games would be suitable for testing subjects’ second-order ToM in a turn-taking game. Let us describe our exclusion criteria by which we selected the 16 different games that we used for game items in the two test blocks as well as in the final 8 games of Stepwise Training.
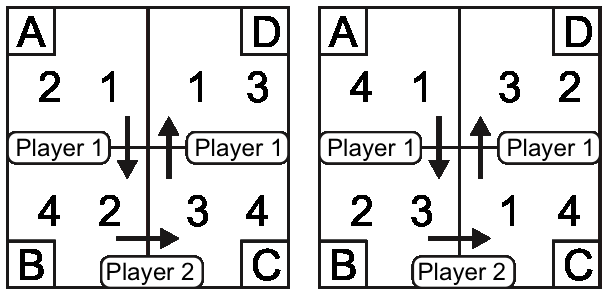
| Figure 8: Two trivial Matrix Games: The game on the left is a so-called trivial first-order game. See text for explanation. The game on the right does not require any ToM reasoning at all, because Player 1’s maximum payoff is already available in cell A. |
Excluding payoff structures requiring only zero-order ToM.
Payoff structures are excluded if Player 1’s payoff in A is either a 1 or a 4, because Player 1 would not need to reason about Player 2’s decision at all. It is obvious that Player 1 should continue the game if his payoff in A is a 1 and stop if his payoff in A is a 4. The game in Figure 8 (right) is an example in which Player 1 should immediately decide to stop in A. Therefore, in line with Hedden and Zhang (2002), we focused on so-called 2- and 3-starting games, associated with payoff structures in which Player 1’s first payoff was a 2 or a 3, respectively.
Excluding “trivial” payoff structures requiring only first-order ToM.
Of the remaining payoff structures, we excluded the so-called trivial ones in which Player 2’s payoff in B was either lower or higher than both his payoffs in C and D. The left matrix of Figure 8 depicts an example of such a game: Player 2 does not need to reason about Player 1’s last possible decision, as his payoffs in C and D are both more preferable than his payoff in B. This included payoff structures in which Player 2’s payoff in B was either a 1 or a 4, because Player 2 would not need to reason about Player 1’s last possible decision between C and D. Accordingly, first-order reasoning on the part of Player 1 would suffice.
| Table 2: Payoff structures of second-order games, adapted from (Hedden & Zhang, 2002) |
ID | Payoff pairs Players 1, 2 | | | | Correct prediction Pl. 2 at B | Optimal decision Pl. 1 at A |
| | A | B | C | D | | |
1 | 3, 2 | 1 , 3 | 2, 4 | 4, 1 | stay | stay |
2 | 3, 4 | 1, 2 | 2, 3 | 4, 1 | stay | stay |
3 | 3, 1 | 2, 3 | 1, 4 | 4, 2 | stay | stay |
4 | 3, 4 | 2, 2 | 1, 3 | 4, 1 | stay | stay |
5 | 3, 1 | 4, 3 | 1, 2 | 2, 4 | go | stay |
6 | 3, 2 | 4, 3 | 1, 1 | 2, 4 | go | stay |
7 | 3, 3 | 4, 2 | 1, 1 | 2, 4 | go | stay |
8 | 3, 4 | 4, 2 | 1, 1 | 2, 3 | go | stay |
9 | 3, 1 | 4, 3 | 1, 4 | 2, 2 | stay | go |
10 | 3, 2 | 4, 3 | 1, 4 | 2, 1 | stay | go |
11 | 3, 3 | 4, 2 | 1, 4 | 2, 1 | stay | go |
12 | 3, 4 | 4, 2 | 1, 3 | 2, 1 | stay | go |
13 | 3, 2 | 1, 3 | 2, 1 | 4, 4 | go | go |
14 | 3, 4 | 1, 2 | 2, 1 | 4, 3 | go | go |
15 | 3, 1 | 2, 3 | 1, 2 | 4, 4 | go | go |
16 | 3, 4 | 2, 2 | 1, 1 | 4, 3 | go | go |
Excluding payoff structures that do not distinguish between attributed opponent types.
The next two exclusion criteria are based on the type of Player 2 that a subject could be reasoning about. A subject, always assigned to the role of Player 1, might be reasoning about a zero-order Player 2 who would not reason about the subject’s last possible decision. Hedden and Zhang call such a Player 2 “myopic” (short-sighted), because they only consider their own payoffs in B and C. In contrast, a subject might be reasoning about an hypothesized first-order or “predictive” Player who does reason about (“predict”) the subject’s last possible decision.
Because Player 1’s decision at A depends on Player 2’s decision at B, payoff structures that yield the same answer for a zero-order and a first-order Player 2 cannot inform us about the level of ToM reasoning on the part of Player 1. We consider these payoff structures to be non-diagnostic, and therefore we exclude them from the final set of stimuli. Hedden and Zhang, who prompted each subjects for predictions of Player 2’s choice at B, could include such payoff structures as long as the correct prediction of Player 2’s move at the second decision point was opposite for imagined zero- and first-order Player 2s. In contrast, we prompted only half of our subjects (the Prompt group) for predictions in the first test block and none of them in the second test block, so we had to exclude all these items.
Balancing the decisions and predictions between “stop” and “go”.
We selected a final set of stimuli, which we were able to (double-)balance for both the number of optimal stay and go decisions of Player 1 and the number of optimal stay and go decisions of Player 2. Because this was only possible for 3-starting games, we excluded the 2-starting games.
The final balancing left us with 16 unique payoff structures (Table 2).
Stepwise training
Let us now present the payoff structures for the training games in the Stepwise training condition, in which the subjects are first presented with 4 zero-order games, then 8 first-order games, and finally 8 second-order games.
As a reminder, zero-order games have one decision point with only the two possibilities A and B; first-order games have two decision points and the subsequent possibilities A, B, and C; finally, second-order games have three decision points and the subsequent possibilities A, B, C, and D.
Zero-order training games
The four payoff structures used in our zero-order training games are presented as four rows in Table 3. The final column represents for each of the four payoff structures the optimal decision for Player 1 at the decision point: stay at A or go on to B.
Note that we have chosen the sets of payoff structures such that optimal (“correct”) decisions are balanced between stay and go over the zero-order games.
| Table 3: Payoff structures of zero-order games with one decision point. Each payoff pair represents the payoffs of Player 1 and Player 2, respectively |
Payoffs Player 1 and 2 | | Optimal decision Player 1 at A |
A | B | |
1, 3 | 3, 2 | go |
3, 2 | 1, 1 | stay |
4, 2 | 2, 4 | stay |
3, 2 | 4, 4 | go |
First-order training games
The fourth column in Table 4 represents for each of the 8 first-order payoff structures (rows in the table) the corresponding correct prediction about Player 2’s decision at the second decision point: stay at B or go on to C. The fifth column represents the optimal “correct” decisions of Player 1 at the first decision point: stay at A or go on to B.
We have chosen the 8 first-order payoff structures such that they are all diagnostic of first-order ToM for Player 1, in the sense that Player 1’s optimal decision to stay or go at the first decision point depends on correctly predicting the decision of a rational Player 2 at the second decision point. That is to say, Player 1’s payoff in A is not larger than both of Player 1’s payoffs in B and C, nor is it smaller than both Player 1’s payoffs in B and C; instead, it is in between those payoffs, therefore, it really matters whether Player 2 will choose to stay at B or go on to C.
Note that we have chosen the sets of payoff structures such that both
correct predictions and correct decisions are balanced between stay and go over all first-order game items.
| Table 4: Payoff structures of first-order games with two decision points. Each payoff pair represents the payoffs of Player 1 and Player 2, respectively |
Payoff pairs Players 1, 2 | | | Correct prediction Player 2 at B | Optimal decision Player 1 at A |
A | B | C | | |
2, 1 | 1, 2 | 3, 3 | go | go |
2, 3 | 1, 2 | 3, 1 | stay | stay |
2, 1 | 3, 2 | 1, 3 | go | stay |
2, 3 | 3, 2 | 1, 1 | stay | go |
3, 2 | 2, 3 | 4, 4 | stay | go |
3, 4 | 2, 3 | 4, 2 | stay | stay |
3, 2 | 4, 3 | 2, 4 | go | stay |
3, 4 | 4, 3 | 2, 2 | go | stay |
Second-order training games
Table 2 presents the 16 diagnostic second-order games of which 8 are selected in the last step of step-wise training.
Undifferentiated training
Table 5 presents 24 trivial payoff structures. These games have the same three decision points as the second-order games. However, they only require first-order ToM for Player 1 to make the correct decision, because Player 2 can make an optimal decision without taking Player 1’s final decision into account.
For example, if the game of row (a) gets to B, Player 2 will always move from B to C regardless of what Player 1 would choose at the third decision point, because for Player 2, both payoff 4 in C and payoff 3 in D are better than his payoff in B. Therefore, Player 1 should predict that Player 2 will go on to C . On the basis of this prediction, Player 1 can safely go on to B, and at the final decision point, Player 1 can stay at C to get the optimal attainable payoff, namely 3.
| Table 5: Payoff structures of trivial first-order games with three decision points. This table has been adapted from Appendix B of (Hedden & Zhang, 2002) |
ID | Payoff pairs Players 1, 2 | | | | Correct prediction Pl. 2 at B | Optimal decision Pl. 1 at A |
| | A | B | C | D | | |
a | 2, 1 | 4, 2 | 3, 4 | 1, 3 | go | go |
b | 3, 1 | 4, 2 | 2, 3 | 1, 4 | go | stay |
c | 2, 4 | 1, 3 | 4, 1 | 3, 2 | stay | stay |
d | 3, 4 | 4, 3 | 1, 1 | 2, 2 | stay | go |
e | 2, 1 | 3, 2 | 4, 3 | 1, 4 | go | go |
f | 3, 4 | 4, 3 | 1, 2 | 2, 1 | stay | go |
g | 2, 4 | 1, 3 | 3, 1 | 4, 2 | stay | stay |
h | 3, 1 | 4, 2 | 2, 4 | 1, 3 | go | stay |
i | 3, 4 | 4, 3 | 2, 2 | 1, 1 | stay | go |
j | 2, 4 | 1, 3 | 4, 2 | 3, 1 | stay | stay |
k | 3, 1 | 4, 2 | 1, 4 | 2, 3 | go | stay |
l | 2, 1 | 4, 2 | 3, 3 | 1, 4 | go | go |
m | 3, 4 | 4, 3 | 2, 1 | 1, 2 | stay | go |
n | 3, 1 | 4, 2 | 1, 3 | 2, 4 | go | stay |
o | 2, 1 | 3, 2 | 4, 4 | 1, 3 | go | go |
p | 2, 4 | 1, 3 | 3, 2 | 4, 1 | stay | stay |
q | 3, 4 | 2, 3 | 4, 1 | 1, 2 | stay | stay |
r | 2, 4 | 4, 3 | 1, 2 | 3, 1 | stay | go |
s | 2, 1 | 1, 2 | 4, 3 | 3, 4 | go | go |
t | 3, 4 | 4, 1 | 1, 2 | 2, 3 | go | stay |
u | 2, 1 | 1, 2 | 3, 4 | 4, 3 | go | go |
v | 2, 4 | 3, 3 | 1, 2 | 4, 1 | stay | go |
w | 3, 4 | 4, 1 | 2, 2 | 1, 3 | go | stay |
x | 3, 4 | 1, 3 | 4, 2 | 2, 1 | stay | stay |
This document was translated from LATEX by
HEVEA.











