Judgment and Decision Making, vol. 7, no. 4, July 2012, pp. 402-426

Individual true and error theory assumes that responses by the same person to the same choice problem within a block of trials are based on the same true preferences but may show preference reversals due to random error. Between blocks, a person’s true preferences may differ or stay the same. This theory is illustrated with studies testing two critical properties that distinguish models of risky decision making: (1) restricted branch independence, which is implied by original prospect theory and violated in a specific way by both cumulative prospect theory and the priority heuristic; and (2) stochastic dominance, which is implied by cumulative prospect theory. Corrected for random error, most individuals systematically violated stochastic dominance, ruling out cumulative prospect theory. Furthermore, most people violated restricted branch independence in the opposite way predicted by that theory and the priority heuristic. Both violations are consistent with the transfer of attention exchange model. No one was found whose data were compatible with cumulative prospect theory, except for those that were also compatible with expected utility, and no one satisfied the priority heuristic.

Keywords:

1  Introduction

When offered a choice, different individuals express different preferences. For example, given a choice between $40 for sure and a fifty-fifty gamble to win either $0 or $100, some people choose the sure cash and others prefer the gamble. When the same person is presented with the same choice problem on two occasions, that individual may give two different responses. Given these two phenomena (between and within-person variability), it is possible that part or all of what are called individual differences may actually be attributable to variability or “instability” of choice behavior. Furthermore, when we test structural properties of theories, apparent violations of a theory may be due to instability of responses rather than to true flaws in a theory.

Therefore, to study individual differences, we need to separate true differences between people from differences that might be due to variation within a person. Furthermore, to study behavioral properties of theories, we need to determine whether violations are “real” or might instead be attributed to instability in the response.

This report investigates two critical properties that distinguish models of risky decision making: first order stochastic dominance (SD) and restricted branch independence (RBI). We apply individual true and error theory (iTET), which permits separation of random variability from true violations of models of risky decision making. These tests allow us to test original prospect theory (OPT) (Kahneman & Tversky, 1979), cumulative prospect theory (CPT) (Tversky & Kahneman, 1992), the priority heuristic (PH) (Brandstätter, Gigerenzer, & Hertwig, 2006), and transfer of attention exchange (TAX) model (Birnbaum, 2008b).

2  Critical tests that distinguish models of risky decision making

Critical properties are theorems that are implied by certain models and which can be violated by rival models. By testing critical properties that hold true for all functions and parameters within a theory, it is possible to refute models without the need to specify functions, to estimate parameters, or to calculate an index of fit.

2.1  First order stochastic dominance

If the probability of receiving a prize greater than or equal to x in Gamble G is always greater than or equal to the corresponding probability in Gamble F, for all x, and if it is strictly greater for at least one value of x, we say that G dominates F by first order stochastic dominance (SD). If choices satisfy SD, a person would not prefer F to G, except by random error. That is,
P(x>t | G) ≥ P(x > t | F) ∀ t ⇒ G ≻ F
Rank-dependent utility models, including CPT (Tversky & Kahneman, 1992) imply that choices must satisfy SD, apart from error. This property is implied by CPT for any strictly monotonic utility function of money and any strictly monotonic probability weighting function.

Birnbaum’s configural weight models violate SD in specially designed choices (Birnbaum, 1997; 2005; 2008b; Birnbaum & Navarette, 1998; Luce, 2000). For example, these models predicted that people should violate SD in the following choice:
F = ($96, 0.85; $90, 0.05; $12, 0.10) ≻

G = ($96, 0.90; $14, 0.05; $12, 0.05)
Following publication of the predictions (Birnbaum, 1997), Birnbaum and Navarrete (1998) tested this choice and found that indeed, more than half of undergraduates tested violated dominance as predicted by the models. Birnbaum and Navarrete (1998) also confirmed the predictions by Birnbaum (1997) of violation of upper and lower cumulative independence.

2.2  Restricted branch independence

A branch of a gamble is a probability-consequence pair that is distinct in the presentation of a gamble. For example, A = ($100, .01; $100, .01; $2, .98) is a 3- branch gamble in which there are two branches having probability .01 to win $100 and a branch with probability of .98 to win $2. A^′ = ($100, .02; $2, .98) is a two-branch gamble. The assumption of coalescing holds that if two branches lead to the same consequence, they can be combined by adding their probabilities. Coalescing implies that A ∼ A^′, where ∼ indicates indifference.

Restricted branch independence (RBI) is the assumption that, if two gambles have a common consequence on a common branch, the consequence can be changed to another value in both gambles without changing the preference between the two gambles. The term “restricted” refers to the requirements that the number of branches is the same and the probability distribution is the same in all cases. This property is a special case of Savage’s “sure thing” axiom (Savage, 1954).

For three-branch gambles, RBI can be written as follows:
S = (x, p; y, q; z, 1–p–q) ≻ R = (x^′, p; y^′, q; z, 1–p–q)

⇔

S^′ = (x, p; y, q; z^′, 1–p–q) ≻ R^′ = (x^′, p; y^′, q; z^′, 1–p–q)

Note that both S and R share a common branch, (z, 1–p–q). The consequence on the common branch has been changed from z (in the choice problem, S versus R) to z^′ (S^′ versus R^′), but the two choice problems are otherwise the same. If a person satisfies RBI, then they should choose either S and S^′ or R and R^′ but should not switch, except by random error.

This behavioral property, RBI, is implied by subjectively weighted utility (SWU) models, including EU and original prospect theory (next section). It is also implied by the editing rule of “cancellation”, proposed by Kahneman and Tversky (1979), and certain other heuristics. RBI is violated by CPT, PH, and TAX, as we see in the next section.

3  Models of risky decision making

3.1  Subjectively weighted utility models

Let G = (x₁, p₁; x₂, p₂; …; x_n, p_n denote an n-branch gamble with monetary consequences of x_i with probabilities p_i, where the sum of the probabilities is 1. Subjectively weighted utility (SWU) can be written as follows:

where the summation is over all n branches of a gamble [probability consequence pairs (x_i, p_i) that are distinct in the presentation to the judge]. It is assumed that G ≻ F ⇔ U(G) > U(F), apart from random error.

SWU models have been studied by Edwards (1962), and by Kahneman and Tversky (1979), among others. Equation 1 is sometimes called “stripped” original prospect theory (PT) because it is stripped of the restriction to gambles with no more than two nonzero branches as well as the editing rules that were postulated to precede evaluation via Equation 1 (Kahneman & Tversky, 1979). Without these restrictions, PT violates SD in cases where people do not; for that reason, an editing rule was added to original prospect theory to say that when people detect dominance, they will satisfy it, though the theory did not specify when people would or would not detect dominance.

The subjectively weighted average utility (SWAU) model can be written:

Although this model does not always satisfy SD, it does not show the kind of violation of transparent dominance that Equation 1 can imply, and which was described by Fishburn (1978) as a criticism of that model (Birnbaum, 1999a). See Karmarkar (1978, 1979), and Viscusi (1989) for variants of this model.

Expected utility (EU) theory is a special case of both SWU and of SWAU, in which w(p) = p. Expected value (EV) is a special case of EU in which u(x) = x.

Violations of RBI constitute evidence against both SWU and SWAU models, including PT. Kahneman and Tversky (1979) further specified the editing rule of “cancellation” which also implies RBI. Therefore, violations of RBI are critical to EU, SWU, SWAU, and to PT.

3.2  Cumulative Prospect Theory

According to CPT (Tversky & Kahneman, 1992; Wakker, 2011), the value of gamble G, with strictly nonnegative consequences, is as follows:

where U(G) is the value (utility) of the gamble, u(x) is the value (utility) of the consequence, x_i; W(P) is a strictly increasing weighting function such that W(0) =0 and W(1)=1; P_i is the (decumulative) probability of winning a prize greater than or equal to x_i, and Q_i is the probability of receiving a prize strictly greater than x_i. EU is a special case of CPT in which W(P) = P.

When consequences are greater than or equal to zero, the representation of CPT is the same as that of rank-dependent utility (RDU) (Quiggin, 1985, 1993; Quiggin & Wakker, 1994), and rank and sign dependent utility (RSDU) (Luce, 2000; Luce & Fishburn, 1991, 1995). All of these models imply coalescing and first order SD, but they can violate RBI, as can other forms of configural weighting, described next.

3.3  Configurally weighted utility models violate RBI

Configurally weighted models differ from Equation 1 in that the weight of a branch may depend not only on its probability, but also on the relationship between the value of a branch’s consequence and consequences of other branches of a gamble (Birnbaum & Stegner, 1979). Equation 2 (CPT) is an example of a configural weighting model, so too are earlier models of Birnbaum (1974a), Birnbaum and Stegner (1979), the rank affected multiplicative weights (RAM) model (Birnbaum & McIntosh, 1996), the transfer of attention exchange (TAX) model (Birnbaum & Chavez, 1997), and gains decomposition utility (GDU) (Luce, 2000). These models are special cases of what Birnbaum and McIntosh (1996, p. 92) called the “generic rank-dependent configural weight” model, also known as the “rank weighted utility” model (Luce, 2000; Marley & Luce, 2001; 2005). Johnson and Busemeyer (2005) present a dynamic, computational theory to account for configural weighting.

A number of studies tested a special form of RBI in which two branches had equal probability, p = q, and using consequences as follows: 0 < z < y^′< y < x < x^′< z^′. In this case, two branches have equal probabilities and the common branch, (z, 1−2p) or (z^′, 1−2p), changes from z smallest in the first choice to z^′ highest in the second choice (Birnbaum, 2008b).

The generic configural weight model can be written for these choices as follows:

where w₁, w₂, and w₃ are the weights of the highest, middle, and lowest ranked branches, respectively, which depend on the value of p (differently in different models) in the choice between S and R. Note that the configural weights in the second choice may differ from those in the first. The generic model allows us to subtract the common term, w₃ u(z), from both sides of the expression for S ≻ R, which yields,

Similarly, we can subtract the common term, w₁ u(z^′), in the expression for the choice between S^′ and R^′. There will be an SR^′ violation of RBI (i.e., S ≻ R and R^′≻ S^′) if and only if the following:

where w₁ and w₂ are the weights of the highest and middle branches, respectively (when both have probability p in S and R), and w₂^′ and w₃^′ are the weights of the middle and lowest branches (with probability p) in S^′ and R^′, respectively. This pattern is referred to as the SR^′ pattern of violation.

The opposite type of violation, R ≻ S and S^′≻ R^′, denoted the RS^′ pattern, will occur whenever

We can use violations of RBI to test among models of risky decision-making. In SWU and SWAU models, including PT (Equation 1), there can be no violations of RBI, except due to random error, because w₁ = w₂ = w₂^′ = w₃^′ = w(p), so both ratios are 1; in EU the weights are all equal to p, so again the ratios are 1. As shown in the next sections, CPT, PH and TAX can imply violations of RBI, which should be of different types.

3.4  CPT violates RBI

The W(P) function of CPT (Tversky & Kahneman, 1992; Tversky & Fox, 1995; Wakker, 2011; Wu & Gonzalez 1996, 1998) has an inverse-S shape (it is steeper near 0 and 1 than in the middle). This shape is needed to describe the classic Allais paradoxes and other well-established phenomena. Appendix A shows that CPT with any W(P) function with an inverse-S shape implies violations of RBI of the RS^′ pattern.

This study employs three branch gambles with equally likely consequences, G = (x, y, z). Given the parameters of Tversky and Kahneman (1992), which imply an inverse-S weighting function, CPT predicts the following RS^′ pattern of choices, for example:
R = ($2, $5, $95) ≻ S = ($2, $35, $40)

R^′ = ($5, $95, $98) ≺ S^′ = ($35, $40, $98)

3.5  Priority Heuristic violates RBI

The priority heuristic (PH) of Brandstätter, Gigerenzer, and Hertwig (2006) assumes that people begin by comparing the lowest consequences of two gambles; if these differ by at least 10% of the largest consequence, the decision is based on lowest consequences only. If not, then the probabilities to receive the lowest consequences are examined; if these differ by 0.1 or more, the decision is based on this factor alone. If not, people compare the highest consequences and make their decision based on that, if the difference exceeds 10% of the highest consequence. If not, they compare probabilities to win the highest consequences and decide based on that. If none of these four features is decisive, the person is assumed to choose randomly.

In the choice between S and R, the lowest consequences are the same and the probabilities are the same; therefore, people should choose R, which has a sufficiently higher best consequence. In the choice between S^′ and R^′, however, the person should choose S^′, which has a sufficiently better lowest consequence. Therefore, PH implies the RS^′ pattern of violation of RBI, as does CPT:
R = ($2, $5, $95) ≻ S = ($2, $35, $40)

R^′ = ($5, $95, $98) ≺ S^′ = ($35, $40, $98)
Now suppose different people followed the PH model, but they used different thresholds for comparing the consequences. For example, suppose a person required a difference of 50% (instead of 10%) of the largest outcome in order to reach a decision. In that case, the person would choose R in the first choice, since the difference $95−$40 exceeds 50%, but this person would choose randomly between S^′ and R^′ because $35−$5 is less than 50% of the highest consequence. This model could then account for R^′∼ S^′ where ∼ indicates indifference. Next, suppose someone started by comparing the highest consequences first and then compared the lower ones, with variable thresholds. That reverse order also leads to either the RS^′ pattern or indifference, depending on the free parameters representing thresholds.

In response to evidence against the priority heuristic, Brandstätter, et al. (2008) proposed an “adaptive toolbox,” in which people mimic EV or use other heuristics, such as “toting up”, cancellation, or a similarity heuristic before using the PH. These heuristics are analyzed in Appendix B, where it is shown that these preliminary heuristics imply RBI. Therefore, systematic evidence of the SR^′ pattern refutes the particular “toolbox” assembly of these postulated heuristics, followed by the PH.

3.6  Special TAX Model violates RBI

In EU, risk-aversion is represented by the shape of the utility function. In the TAX model, however, risk attitudes are represented in part by transfers of weight (attention) from branch to branch, according to a person’s point of view.

Birnbaum and Stegner (1979) tested this theory by instructing people to take on the viewpoints of buyer, seller, or neutral judge. They found the predicted interactions and changes of rank order implied by the theory that viewpoint affected the configural weights: Buyers place greater configural weight on lower estimates of value and sellers place greater weight on higher estimates of value. Birnbaum, Coffey, Mellers, and Weiss (1992) and Birnbaum and Beeghley (1997) showed that this model describes evaluations of gambles as well. The findings of Birnbaum and Stegner (1979), and others that followed, contradict the implications of the “loss aversion” interpretation (Tversky & Kahneman, 1991) proposed to describe the so-called “endowment” effect (Birnbaum & Zimmermann, 1998).

In the “special” TAX model, all transfers of weight are proportional to the probability weight of the branch losing weight. Let ω represent the proportion of weight transferred from highest consequence to lowest. Appendix C shows that as long as this value is not zero, violations of restricted branch independence should be opposite the pattern predicted by CPT and PH; namely, SR^′.

The “prior” TAX model refers to non-optimal parameters that were originally chosen to calculate predictions for a new experiment (Birnbaum & Chavez, 1999). These parameters held up fairly well predicting the results of other new experiments as well (Birnbaum, 2008b; 2010). For choices between three-branch gambles (n = 3), ω = δ/(n + 1), where δ = 1, so ω = ¼, u(x) = x for 0 < x < $150, and t(p) = p^0.7. With δ= 1 (ω = 1/4) and p = 1/3, for example, it follows that w₂/w₁ = 2 > 3/2 = w₃^′/w₂^′. With these parameters, the model predicts the following:
R = ($2, $5, $95) ≺ S = ($2, $35, $40)

R^′ = ($5, $95, $98) ≻ S^′ = ($35, $40, $98)
When ω = 0, the TAX model reduces to SWAU, in which case there would be no violations of RBI; when ω =0 and t(p) = p, the model reduces to EU, in which case there would be no violations of either RBI or SD.

3.7  Unsettled issues from previous studies

Previous research (see Birnbaum, 2008b for a summary) reported that the frequency of violations of the pattern SR^′ predicted by special TAX exceeds that of the pattern RS^′ predicted by CPT. For example, Birnbaum (1999b) tested the following choices:
S = ($44, 0.10; $40, 0.10; $2, 0.80) versus
R = ($96, 0.10; $4, 0.10; $2, 0.80)

and

S^′ = ($100, 0.80; $44, 0.10; $40, 0.10) versus
R^′ = ($100, 0.80; $96, 0.10; $4, 0.10)
In one case where these two choices were presented to 124 undergraduates, 19 showed the SS^′ pattern, 32 had the pattern SR^′, 13 were RS^′ and 60 were RR^′. Because 32 is significantly greater than 13, these results were interpreted as evidence against CPT, SWU, and EU and in favor of TAX.

Three related issues remain unsettled by results like these, however. First, there were 19 + 60 = 79 people out of 124 (63%) whose response patterns, SS^′ or RR^′, are compatible with EU (and SWU/SWAU/PT models). Perhaps this means that this class of models is compatible with the data of most people. On the other hand, the same person who satisfied RBI in one test might show violations if we repeated the same choices or if we presented other choice problems that were more appropriately selected for that person’s individual parameters; therefore, it would be premature to conclude that people who satisfied the property in a single test also satisfy EU (or SWU, SWAU or PT) in general.

Note that Expressions 4 and 5 depend on two factors that might easily show individual differences: configural weights and the utility function. The “prior” TAX model predicts the SR^′ violation in this choice problem, but if a person had, for example, u(x) = x^0.6 instead of u(x) = x, with the same configural weights, then that person would not show a violation in these choice problems (the person would instead choose the safe gamble in both cases, SS^′). However, that same person would show the SR^′ violation if we tested RBI with (x, y) = ($31, $27) instead of ($44, $40) in otherwise identical choice problems. So unless we used this choice, we might undercount the proportion of people who have this pattern compatible with TAX.

Second, significantly more people showed the SR^′ pattern of violation than showed the RS^′ pattern. Thus, the more frequent pattern agrees with TAX and contradicts CPT. Because SWAU and EU are special cases of the TAX model, a person enamored with TAX might argue that TAX is the best representation because 79 + 32 = 111 of 124 are compatible with this model. However, this summary might overestimate the success of TAX because some of those 79 who satisfied RBI in this test might have shown the pattern of violations predicted by CPT or PH, had they been presented with different choice problems, so unless we test a greater variety of choice problems, we might underestimate the frequency of people who contradict TAX and perhaps satisfy CPT or PH.

Third, 13 people showed the RS^′ pattern predicted by CPT with the inverse-S function or by PH. These people might actually be consistent with CPT or PH models, in which case we might conclude that different people apparently use different models. Because EU is a special case of CPT, there might be 13 + 79 = 92 who were consistent with CPT, for example. On the other hand, these 13 people showing RS^′ might simply show this pattern by chance, as a result of random error.

A person who truly preferred R and R^′ on these choices might show the RS^′ pattern by making an error on the second choice, and a person whose true pattern was SS^′ could show this pattern by making an error on the first choice. If we presented this same choice problem repeatedly, these people might show their true patterns when retested. To address these three issues we need a way to distinguish whether responses compatible with or in violation of a model are true or due instead to error. Otherwise, we cannot determine whether some or none of these individuals are obeying the predictions of a given model.

3.8  Purposes of the present studies

This paper presents individual true and error theory (iTET) and applies it to illustrate how it can address the above questions left open by a typical group analysis. Are there indeed any individuals whose data can be best represented by PH or CPT models? In two studies, each participant is presented with a number of repetitions of each choice problem, and iTET is used to separate variation due to error from true violations.

---

Table 1: Predictions of models and heuristics for the properties tested. EU/EV = Expected Utility theory or expected value; SWU/PT = subjectively weighted utility and prospect theory; CPT = Cumulative Prospect theory; TAX = transfer of attention exchange model; PH = priority heuristic. Critical = implied with all functions and parameters; parametric violations = the model may satisfy or violate the property.

Model	Stochastic Dominance	Restricted Branch Independence
EU/EV	Critical, satisfies	Critical, satisfies
SWU/SWAU/PT	Parametric violations	Critical, satisfies
CPT	Critical, satisfies	Parametric violations; Inverse-S implies RS′
TAX	Parametric violations	Parametric violations; Special TAX implies SR′
PH	Critical, satisfies	Critical RS′
PH with free parameters, reverse order	Parametric: satisfies or undecided	RS′ or undecided.

---

Table 1 summarizes the implications of the models for tests of SD and RBI. As noted in the table, SD is a critical property of EU and CPT, meaning that there are no functions or parameters that can allow either of these models to violate it. Similarly, RBI is a critical property of EU, SWU and SWAU models including PT, with or without the editing rule of cancellation. People who satisfy CPT or PH should show two properties: (a) they should not systematically violate SD and (b) they should show the predicted RS^′ pattern of violation of RBI. A person satisfying the special TAX model might violate SD and show the SR^′ pattern of violation of RBI. As shown in Appendix B, the “adaptive toolbox” model that includes EV, EU, toting up (with variable monotonic utility functions), cancellation, similarity, and the PH with variable thresholds can either satisfy RBI or violate it with the pattern RS^′, but this toolbox cannot fit the pattern SR^′, except by random error.

4  Individual true and error theory

A major problem in analyzing empirical data is the fact that variation in the response might produce apparent violations of critical properties, even if a person would be otherwise consistent with a model. A number of papers have dealt with this issue, and there remains disagreement about how to solve it (Birnbaum, 2004b; 2011; Birnbaum & Schmidt, 2008; Carbone & Hey, 2000; Harless & Camerer, 1994; Hey & Orme, 1994; Loomes & Sugden, 1995; Morrison, 1963; Regenwetter, Dana, & Davis-Stober, 2010, 2011; Regenwetter, Dana, Davis-Stober, & Guo, 2011; Sopher & Gigloitti, 1993; Tversky, 1969; Wilcox, 2008).

The true and error model applied to group data has had reasonable success (Birnbaum, 2008c, 2010, 2011; Birnbaum & Gutierrez, 2007; Birnbaum & Schmidt, 2008). This model allows each person to have a different pattern of “true” preferences, allows each choice problem to have a different “error” rate, and it can also allow people to differ in their levels of noise (Birnbaum & Gutierrez, 2007, p. 103).

However, to address the issues raised in the previous section, we need a theory that can describe the behavior of an individual. To distinguish the theory proposed here from that in previous work, we designate iTET to refer to the individual true and error theory, and gTET to refer to the version of true and error theory used in previous studies of group data.

The next sections illustrate how iTET can be applied to test critical properties based on one choice (SD) and two choices (RBI). It is allowed that each person might have different “true” preferences in different blocks of trials, and preference reversals within a block of trials are attributed to random error. An important special case of this model is one in which a person’s “true” preferences stay the same throughout the study (Birnbaum, 2011).

4.1  True and error analysis of stochastic dominance

CPT implies that people should never violate SD, except by error. In contrast, the TAX model implies that people will violate SD in choice problems like the following:
G = ($96, 0.90; $14, 0.05; $12, 0.05) versus
F = ($96, 0.85; $90, 0.05; $12, 0.10).

Note that G dominates F because the probability to win $96 or more is larger in G than F, the probability to win $90 or more is the same; the probability to win $14 or more is greater in G than F, and there is no value x such that the probability to win x or more is greater in F than in G.

Within each block of trials, each person receives two choice problems testing SD, the GF problem above, and the following choice between F^′ and G^′:
F^′ = ($89, 0.70; $88, 0.10; $11, 0.20) versus
G^′ = ($90, 0.80; $13, 0.10; $12, 0.10).

Note that this is a similar test, except positions of the dominant and dominated gambles are reversed.

Assume that in a given block of trials, an individual either truly satisfies or truly violates SD (in both problems). Over blocks containing both choices, embedded among other trials, the probability of showing two violations of SD is assumed to obey the following:

where p(FF^′) is the probability of showing two violations of SD; p_F is the probability that this individual “truly” violates SD in a block of the experiment, e₁ and e₂ are the error rates for the two choice problems, which are assumed to be independent and less than ½. Note that, if the person truly violates SD, he or she can show two violations only by making no error on either trial, and if the person truly satisfies SD, she or he can show two violations only by making two errors. The probability of showing two satisfactions of SD is then:

it follows that p(FF^′) >p(GG^′) ⇔ p_F > 1/2.

Error rates can be estimated from preference reversals between presentations of the same choice within blocks. If we assume the error rates for these two choice problems are equal, e₁ = e₂ = e₃, the probability of reversals within a block of trials is given as follows:

Therefore, the probability of the union of both types of preference reversals is 2e(1−e). For example, if there are 32% reversals between two versions of the same choice within blocks, 2 e (1 − e) = 0.32, from the quadratic equation, e = 0.2 for this choice problem.

If e = 0.2, and if the probability of “true” violations is 0 (i.e., p_F = 0), as implied by models that satisfy SD, then we should expect to see two violations in a block only 4% of the time, because Equation 6 reduces to: p (FF^′) = e² when p_F = 0. Therefore, we can test if p_F > 0 by estimating the error rate, e, from the proportion of preference reversals, and then comparing the observed proportion of two violations to the squared error rate.

For example, suppose Jane was presented with 20 blocks of trials with two tests of SD in each block and showed two violations (FF^′) in 2 blocks, 4 blocks with FG^′, 5 blocks with GF^′, and 9 blocks with two satisfactions (GG^′). She violated SD 13 times out of 40 choice problems, so she violated SD in 33% of the tests. From the 9 reversals (FG^′ & GF^′) out of 20 we estimate, 2 e (1 − e) = .45; from the quadratic equation, e = .34; therefore, e² = 0.12, so if p_F = 0, we expect (20)(0.12) = 2.34 blocks with FF^′; but we observed only 2 blocks with FF^′; therefore, we can retain the hypothesis that her “true” rate of violation is p_F = 0. In this case, iTET indicates that an observed rate of violation of 33% could occur when the true rate was 0.

Now consider the case of Joe who had 4 blocks with FF^′, 2 blocks with GF^′, 2 blocks with FG^′, and 12 blocks with GG^′. Although Joe violated stochastic dominance only 30% of the time (less often than Jane), we conclude that Joe truly violated SD. In his case, 2 e (1 − e) = .2, so e = 0.11. We can reject the hypothesis that p_F = 0, because e² = 0.013; the binomial probability to observe 4 or more cases out of 20 with this probability is small (p < .001), so we can reject the hypothesis that Joe truly satisfied stochastic dominance in favor of the hypothesis that p_F = 0.24.

When responses are independent, p(FF^′) = p(F) p(F^′); however, independence does not hold in iTET unless p_F is either 0 or 1, even though the errors are independent. Note that in this case, the choice proportions are as follows: p(F) = p(F^′) = 0.3, but p(FF^′) = 0.20 > p(F) p(F^′)=.09. Thus, in the case of Joe, we can reject independence via the two-tailed, Fisher exact test of independence on his observed frequencies (12, 2, 2, 4), which is significant (p = .037).

This case violates the assumptions of Regenwetter, et al. (2011), whose approach requires that probabilities are identically distributed and independent (people do not learn or change during a study). If a person has different “true” preferences in different blocks, p_F will fall between 0 and 1 and iTET implies that independence will be violated, such that p(FF^′) > p(F) p(F^′). In Joe’s case, he may have learned to satisfy dominance during the study.

Now consider Jill, who made two violations on 13 blocks, one violation on 6 blocks (reversals), and had zero violations in one block. Six reversals out of 20 trials is 0.30, so e is estimated to be 0.19. Furthermore, 13 FF^′ out of 20 is 0.65; from Equation 6, the estimated probability of “true” violations is p_F = 1. That is, her results are consistent with the hypothesis that she consistently violated SD throughout the experiment.

Finally, consider a case that would be in violation of iTET. As shown in Equation 7, the two types of preference reversals should be equally likely. In addition, error rates are assumed to be less than ½; since the total probability of preference reversals is 2e(1−e), it follows that this total must be less than ½. For example, suppose Jake had 2 blocks with FF^′, 2 blocks with FG^′, 14 blocks with GF^′, and 2 blocks with GG^′, we could reject the iTET model for two reasons: First, 14 is significantly greater than 2, since the binomial probability to observe 14 or more hits out of 16 trials with probability of ½ is .002. Second, the number of preference reversals (14 + 2 = 16) is significantly more than half the 20 cases, since the binomial probability to observe 16 or more out of 20 is .006. Thus, it is possible to test iTET, and if data so indicate, to reject it, as in the case of Jake.

4.2  True and error model of RBI

The property of RBI involves two choice problems: a choice between S and R and a choice between S^′ and R^′. To test this property, we present each choice twice within each block of trials. RBI is the assumption that S ≻ R ⇔ S^′≻ R^′, apart from error. Appendix D shows that we can again use reversals within blocks to estimate the error rates and this allows us to test the two-choice property of restricted branch independence by analyzing four choice problems per block. Appendix D presents both analysis and results.

5  Method

Each participant made choices between gambles in two sessions separated by one week. Each choice was evaluated multiple times by each person, separated by many filler trials. Each gamble was described in terms of an urn containing equally likely tickets, which differed only in the prize values printed on them. The participant could choose the urn from which a ticket would be drawn randomly to determine the cash prize.

They were informed that 10 people would be selected randomly to play one of their chosen gambles for real cash prizes. Participants were told that any of their decisions might be selected for play, so they should choose carefully. Prizes were awarded following completion of the study as promised.

5.1  Choice formats

Choices were displayed in one of two formats. In one group of trials, gambles were described in terms of urns containing exactly 100 tickets. These trials were displayed as in the following example:

First gamble:

90 tickets to win $96
5 tickets to win $14
5 tickets to win $12

OR

Second gamble:
85 tickets to win $96
5 tickets to win $90
10 tickets to win $12
In the other group of trials, each urn contained exactly two or three equally likely tickets, whose values were listed. These trials were displayed as in the following example:
First Gamble: ($2, $40, $45)

OR

Second Gamble: ($2, $5, $95)

Instructions and materials can be viewed via the following URL:
http://ati-birnbaum-2009.netfirms.com/Spr_2010/thanks3.htm

5.2  RBI subdesigns

In each of two sub-designs testing RBI, the urns were described as holding exactly two or exactly three equally likely tickets. Again, the participant could choose the urn from which a randomly selected ticket would be drawn to determine the prize. Subdesign RBI1 consisted of 24 trials of the form, S = (z, x, y) versus R = (z, $5, $95). The trials were constructed from an 8 X 3, (x, y) by z, factorial design, in which the 8 levels of (x, y) in the safe gamble were ($15, $20), ($20, $25), ($25, $30), ($30, $35), ($35, $40), ($40, $45), ($45, $50), or ($50, $55), and the 3 levels of z were $2, $98, or none. When z was not presented, the trial was a choice between 2, two-branch gambles.

Subdesign RBI2 consisted of 27 trials of the form, R = (z, $4, $96) versus S = (z, x, y), constructed from a 3 X 9, z by (x, y), factorial design in which the 3 levels of z were $3, $97, or none, and the 9 levels of (x, y) were ($14, $18), ($27, $31), ($30, $34), ($33, $37), ($36, $40), ($39, $43), ($42, $46), ($45, $49), and ($48, $52). The two sub-designs counterbalanced the positions of the “safe” and “risky” gambles but are otherwise quite similar.

Stochastic dominance was tested by two choice problems embedded in a block of 31 trials like those in Birnbaum (2008b): G = ($96, 0.90; $14, 0.05; $12, 0.05) versus F = ($96, 0.85; $90, 0.05; $12, 0.10) and G^′ = ($90, 0.80; $13, 0.10; $12, 0.10) versus F^′ = ($89, 0.70; $88, 0.10; $11, 0.20). Position of the dominant gamble was counterbalanced.

5.3  Procedure of Study 1

Each participant was tested via computer in a lab and served in two sessions of 1.5 hours each, separated by one week between sessions. Each replication consisted of either 131 or 134 trials, and included one of the two blocks testing RBI (either RBI1 or RBI2), each preceded by 6 warmup trials, as well as the two trials testing SD embedded among other choice problems. Trials were blocked in sets of 25 to 31 choice problems; each block tested different properties. Most of these blocks involved choices between two-branch gambles, designed to test transitivity. For the analyses in this article, these blocks of trials can be regarded as “fillers” that served to separate the blocks of experimental trials described here; results of our tests of transitivity are described elsewhere (Birnbaum and Bahra, submitted).

5.4  Procedure of Study 2

Study 2 was the same as Study 1, except for the manner in which trials were blocked and procedures for instructions and warmups. The blocking scheme in Study 2 for the tests of RBI allowed us to apply the iTET model to this property.

All trials involving choices between urns containing 100 tickets, including tests of SD and transitivity, were intermixed to form large blocks with 107 choice problems.

The two designs testing restricted branch independence (RBI1 and RBI2) were intermixed and preceded by six warmups to create blocks of 6 + 24 + 27 = 57 trials. The two blocks were alternated (total = 107 + 57 = 164), so any two presentations of the same choice problem were always separated by at least 107 “filler” trials. Within the block of 57 RBI trials, most trials had a common probability-consequence branch; if a person wanted to cancel common branches, it would be easy to do so in this study.

Each participant was given additional printed instructions and completed several preliminary trials using paper and pencil that included tests of transparent dominance. If a participant violated dominance on these trials, the experimenter asked the participant to explain the decision. If the participant did not spontaneously identify the error, the experimenter asked the participant to re-read the printed instructions and complete the warm-ups again. When the participant appeared to at least superficially understand the task, she or he was then directed to begin the study via computer. Each participant was tested individually in a lab via computer in two sessions of 1.5 hours each, separated by one week between sessions.

5.5  Participants

Participants in Studies 1 and 2 were 43 and 59 undergraduates enrolled in lower division psychology at California State University, Fullerton. Because they were free to work at their own paces, some participants completed more repetitions than others. Because each replicate in Study 1 included only one of RBI1 or RBI2 designs, whereas each replicate in Study 2 included both RBI1 and RBI2 intermixed, participants in Study 2 completed relatively more tests of RBI relative to the tests of SD, but they completed fewer blocks on average. All participants in Study 1 completed at least 10 replicates and 42 of 59 participants in Study 2 completed 10 or more (10 replicates means 20 choice problems testing SD).

6  Results

Tables 2 and 3 show aggregate results of the tests of RBI, averaged over participants in both studies, which gave comparable results. Median percentages choosing the “risky” gamble, R = (z, $5, $95) over S = (z, x, y) are shown, with separate rows for different values of (x, y), in both tables. Columns represent choices with different common consequences; e.g., z = $2, z^′= $98, or without z (none) in Table 2.

---

Table 2: Median proportions for choosing R=(z, $5, $95) over S=(z, x, y). The common consequence, z, was $2, $98, or none was presented, which designates choices between R=($5, $95) and S=(x, y). (Both studies)

Safe Gamble	z = $2	z = (none)	z′ = $98
(z, 15, 20)	80	94	100
(z, 20, 25)	50	78	100
(z, 25, 30)	80	94	100
(z, 30, 35)	24	63	94
(z, 35, 40)	15	31	89
(z, 40, 45)	06	15	87
(z, 45, 50)	00	17	77
(z, 50, 55)	00	03	67

---

If people satisfied RBI, as they should do according to EU, SWU, SWAU and original PT, or by “canceling” common branches (or using toting up, as in Appendix B), there would be no effect of columns. Instead, the percentages choosing the risky gamble are higher when the common consequence, z = $98 than when z = $2. For example, the median percentage is 24% choosing R = ($2, $5, $95) over S = ($2, $30, $35), and the percentage is 94% choosing R^′ = ($5, $95, $98) over S^′ = ($30, $35, $98). With no common consequence, the choice percentage is 63% choosing R = ($5, $95) over S = ($30, $35).

The medians in both Tables 2 and 3 show the SR^′ pattern of violation of RBI that is opposite the predictions of both CPT with its inverse-S probability weighting function, and it is opposite the predictions of the PH.

---

Table 3: Median percentage choosing R=(z, $4, $96) over S=(z, x, y). The common consequence was either $3 or $97, or none was presented.

Safe Gamble	z=$3	z=(none)	z′=$97
(z, 14, 18)	88	100	100
(z, 27, 31)	29	50	100
(z, 30, 34)	22	48	100
(z, 33, 37)	14	31	89
(z, 36, 40)	12	33	82
(z, 39, 43)	13	29	82
(z, 42, 46)	00	12	78
(z, 45,49)	00	14	71
(z, 48,52)	00	08	63

---

The PH implies that the majority should choose S=(x, y) over R=($5, $95) whenever x ≥ $15, since the lowest consequence of S is at least $10 better than the lowest consequence of R. Therefore, all of the percentages (choosing R) in the middle column of Table 2 should be less than 50. Instead, only the last four entries of Table 2 satisfy this prediction. When the smallest consequence is the same in both S and R (z = $2, in the first column), the majority should choose the R gamble, which has the better highest consequence; instead, only the first three entries in this column of Table 2 satisfy this prediction. In the third column (z = $98), people should choose S because of the better lowest consequences; instead, more than half of the sample chose R more than half the time in all rows.

In summary, the PH was correct in predicting the majority choice in only 7 of 24 choice problems in Table 2. Similarly, the PH was correct in predicting only 9 of 27 modal choices in Table 3. Overall, the PH was correct only 16 times out of 51 choice problems, which is significantly fewer than half the cases--a random coin toss would have a probability of .99 to outperform this model! As shown in Appendix B, the adaptive toolbox model proposed by Brandstätter, et al. (2008) including EV, toting up, similarity, and cancellation, as well as the PH either implies RBI or the opposite pattern of violations from what we observe. In addition, allowing different thresholds for different people either creates random responding or the pattern of violation that we do not observe. That particular toolbox does not contain the tool needed to fit these data. Two other heuristics that can violate RBI are described there.

In addition to the effect of columns in Tables 2 and 3, there is an effect of rows: as (x, y) in the “safe” gambles increase, the proportion choosing the risky gamble decreases. This indicates that people are not simply choosing the gamble with the higher median (Birnbaum & McIntosh, 1996).¹ In addition, there is a small but systematic violation of 3–2 lower distribution independence; that is, the entries in the middle column are consistently larger than those in the first column (Birnbaum, 2008b).

According to the TAX model with prior parameters (δ=1, so ω=0.25, u(x) = x, t(p) = p^0.7) there should be just one SR^′ violation of RBI in Table 2, in the fifth row where (x, y) = ($35, $40), Rows 1 to 4 should show the pattern RR^′ and Rows 6–8 should show the response pattern SS^′. But if different people have different parameters, TAX allows other violations. For example, if ω = 0.45 and u(x) = x, there should be SR^′ violations for that person in the first four rows of Table 2. As shown in Appendix C, special TAX model with free parameters implies that either RBI should be satisfied or that violation should be of the SR^′ type.

Although the aggregate results in Tables 2 and 3 violate both original PT, CPT with the inverse-S weighting function and the PH, aggregated results leave open the possibility that some individuals might satisfy the predictions of these models.

---

Figure 1: Individual results for participants in Study 1 (filled circles) and Study 2 (triangles). Differences between two types of violations of RBI (as a proportion of the number of tests) are shown on the ordinate against the proportion of violations of stochastic dominance on the abscissa. EU (expected utility) theory implies no violations of either property; CPT (cumulative prospect theory with the inverse-S weighting function) implies no violations of stochastic dominance and predicts the RS′ pattern of violation of RBI (restricted branch independence). PH (priority heuristic) predicts that people should show 100% RS′ violations of RBI, apart from error, and should satisfy SD. TAX predicts violations of both properties with SR′ violations of RBI.

---

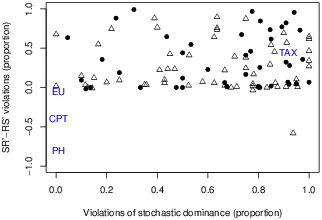
Each pair of tests of SD (two tests per block) for each person in each repetition block can be scored as GG’, FG^′, GF^′, or FF^′. CPT, PH, and EU imply SD, so these theories predict we should see few choices including F or F^′ (violating dominance), and the pattern FF^′ should be rare and limited by the frequency of preference reversals (FG^′ and GF^′). Of the 102 participants, 67 had a greater frequency of FF^′ (two violations) than of GG^′ (none), meaning that 67 are estimated to have p_F > 1/2. The median proportion of violations of stochastic dominance was 0.69. Only two people had no violations of SD.

Similarly, each test of RBI in each replicate can be scored as one of four patterns: SS^′, SR^′, RS^′, or RR^′. Whereas CPT (with the inverse-S probability weighting function) implies RBI violations of the type RS^′, the special TAX model implies violations only of the type SR^′. The PH also predicts violations of RBI of the RS^′ type, but it predicts violations in every row of Tables 2 and 3.

By adding response patterns across blocks and tests, we can compare the number of SR^′ violations with RS^′ violations for each person. Most participants (90 out of 102) had more violations of SR^′ than of the type predicted by CPT or PH (RS^′). A z test was computed for each person, with the result that 75 of the 102 people had z > 2 (significant at the 5% level). Only 4 out of 102 participants showed more RS^′ violations than SR^′ violations; and only one of these showed significantly more RS^′ than SR^′.

Figure 1 plots the observed proportion of violations of SD on the abscissa and the difference between the number of SR^′ and RS^′ violations of RBI as a proportion of the number of tests for each participant. Filled circles and triangles represent individuals in Studies 1 and 2, respectively. The label “EU” in the figure is placed near the coordinates (0, 0), because EU theory implies no violations of either RBI or SD. The label “CPT” is placed to show that CPT implies no violations of SD and it predicts RBI violations of the RS^′ type. “PH” is placed to indicate that it violates RBI more strongly than does CPT but both imply the same RS^′ pattern, and both CPT and PH should satisfy SD in these tests. SWU, SWAU, and PT allow violations of SD but imply no violations of RBI, so cases with ordinate values close to zero are compatible with these models.² The special TAX model implies violations of RBI of the SR^′ type and it violates SD with its prior parameters. Most of the points in the figure are in the vicinity of the TAX model; that is, most people show violations of RBI more frequently of the SR^′ type and most show substantial violations of SD.²

6.1  True and error analysis of stochastic dominance

According to iTET, p(FF^′) > p(GG^′) if and only if the probability of “truly” violating SD exceeds ½. There were 67 who showed this relation. We can estimate the “error” rate from preference reversals within blocks and use it to test whether the probability of violating SD exceeds 0.³ From these calculations we estimate that in 86 of 102 cases, people were “truly” violating SD; that is, 86 people had estimated p_F > 0.

When iTET was fit to each person’s data, to minimize the sum of squared discrepancies between observed proportions and predictions, the median estimates of p_F and e are 0.88 and 0.17; 39 people were estimated to violate SD with p_F = 1.

The mean proportion of violations of SD showed a slight decrease as trial blocks increased over the first ten blocks. Among those participants who completed at least 10 blocks, the mean proportion of violations decreased from 0.69 averaged over the first two blocks to 0.60 averaged over the 9^th and 10^th blocks. No further reduction was found among those who completed 20 blocks or more. There were 48 participants who showed no change between their first and last blocks, 25 showed increases, and 29 showed decreases in the percentage of violations of SD.

For those cases for which 0.01 < p_F < .99, independence was tested by comparing P(FF^′) with P(F)P(F^′). It was found that in 34 cases, P(FF^′) > P(F)P(F^′), and in 12 cases the opposite relation held. This difference is significant (z = 3.24), consistent with the pattern of non-independence predicted by the iTET and TAX model when 0 < p_F < 1.

In 7 of 102 cases, iTET appeared to give a poor account of the observed data. The model implies that p(FG^′) = p(GF^′) = e(1−e), p(FG^′) + p(GF^′) = 2e(1−e) < 1/2, so p(F) =p(F^′). However, one case violated SD in the FG choice problem 20 times and violated it on the F^′G^′ choice problem only 3 times out of 21 blocks. Similarly, another case violated SD in the FG choice 16 times but violated it in the F^′G^′ choice problem just 3 times out of 20. It is unclear if these deviations are a fault of iTET or of the simplifying assumption that the two choice problems testing SD are equivalent. Note that in the FG choice problem, the dominant gamble G has two features that favor it over F, but in the F^′G^′ problem, the dominant gamble has four features favoring G^′ over F^′. Perhaps a few people attended to these features.

---

Figure 2: Estimated violations of restricted branch independence (ordinate) showing the SR′ pattern rather than the RS′ pattern, plotted against estimated probability of violating stochastic dominance, corrected for unreliability by individual true and error theory (Study 2). EU=expected utility, CPT=cumulative prospect theory, PH=priority heuristic, SWU=subjectively weighted utility, TAX=transfer of attention exchange.

---

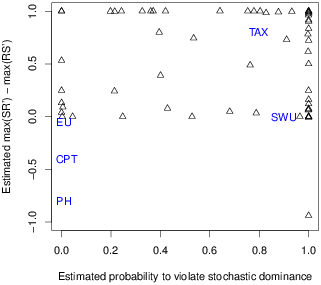
6.2  True and error analysis of RBI

Individual analysis of RBI is described in Appendix D. Each test by each person was based on four choice problems per block and was analyzed separately.

Figure 2 shows the effect of using iTET to “correct” both results for unreliability of response. Each triangle represents an individual from Study 2, where the iTET model could be applied to the tests of RBI. The ordinate shows for each case, the difference between the maximal estimated p_SR^′ minus the maximal estimate of p_RS^′; the abscissa shows the estimated probability of violating stochastic dominance, p_F. The same outlier case as in Figure 1 appears in the lower right of Figure 2.

The results in Figures 1 and 2 show that not even one person fit the pattern predicted by either CPT or PH. Only one person showed frequent RS^′ violations of RBI compatible with CPT and its inverse-S weighting function (triangle in lower right of Figures 1 and 2), but that person violated SD in 30 of 32 tests, including violating both problems in 14 of 16 blocks. Therefore, this case does not fit either CPT or PH. One might try to argue that this person was confused or indifferent in the tests of SD (and thus choosing randomly), but this person’s data are so extreme that they also refute this argument, since the binomial probability to observe 30 or more hits out of 32 trials with e = 1/2 is less than one in a million.

When the configural weighting parameter in TAX is zero (ω=0), the TAX model reduces to SWAU. This model implies no violations of RBI, but it can still violate SD. There appear to be several cases in each study with ordinate value close to 0 in Figure 1, who might be consistent with this special case of TAX or perhaps original PT (Equation 1), which satisfies RBI and can violate SD. When ω=0 and t(p) = p, TAX reduces to EU. There are a few cases close enough to EU that EU cannot be rejected for those individuals. Because EU is also a special case of CPT, when W(P) = P, cases that satisfy EU also remain consistent with CPT. Appendix E presents tests of RBI, showing the number of response patterns of each type for each individual.^4,5

7  Discussion

These studies illustrate how iTET can be used as a referee to evaluate models of risky decision-making in individuals. It allows the investigator to determine whether violations of a critical property are real or attributable to random error in response. The results of the studies are quite clear: no individual was consistent with predictions of the PH, and no one was consistent with CPT, except for those who satisfied EU, which is a special case of both CPT and of TAX. Because CPT was intended as a theory to account for violations of EU, finding cases that satisfy EU would not be much consolation to a supporter of CPT.

Many cases were observed with the SR^′ pattern of violation of RBI and who strongly violated SD; these cases (depicted in the upper right portion of Figures 1 and 2) are not consistent with EU, SWU, SWAU, or original PT with or without its editing rule of cancellation. This pattern of violation of RBI and SD are consistent with the special TAX model.

Only one case was an outlier to the special TAX model (and to all of the other models); this one person showed strong violations of SD and also showed a prevalence of violations of RBI of the type RS^′. This person might be compatible with some more general form of configural weighting (Birnbaum, 2004a; Johnson & Busemeyer, 2005), but is not compatible with either CPT or PH because of the systematic violations of SD.

From previous results, it was entirely possible that a subgroup of people might have been found who were consistent with stochastic dominance and the RS^′ pattern of RBI violation characteristic of CPT with the inverse-S weighting function. Had the results been different, one might have concluded that different groups of people use different models or that we should seek a more general model in which people differ in their parameters with respect to that more general model. But such conclusions were not dictated by our results, which failed to find any person consistent with CPT or PH who showed violations of EU.

These conclusions are much stronger than those possible from previous research, as reviewed by Birnbaum (2008b), for example. By application of iTET to multiple tests of RBI, we were able to establish for almost all individual what type of true violations they had. [In fact, we might have done still better with our experimental design, because we found some cases that were too risk-averse (e.g., showed only SS^′ patterns), who might have been better diagnosed with (x, y) smaller than ($14, $18); and there were others who were too risk-seeking (e.g., who showed only RR^′ responses) who might have been better assessed using (x, y) greater than ($50, $55). Although these cases show no violations of RBI and therefore remain consistent with EU and PT, we think it possible that with different choice problems, some of them may have shown violations. The adaptive technique recently proposed by Cavagnaro, Pitt, and Myung (2011) might be useful in future studies to find out whether there are indeed any people consistent with RBI.

Had we investigated only one property, we could not have reached these stronger conclusions. Had we studied only SD, we would have found 16 people who satisfy this property (in 16 cases, estimated p_F = 0), which might have been consistent with CPT. Had we studied only RBI, we would have found one person whose violations of RBI satisfied the predictions of CPT and PH. Because we tested both properties, we are able to rule out CPT and PH because no person satisfied both critical tests of these models.

7.1  Comparing fit of models versus crititcal tests

Our conclusions are also much stronger and clearer than are possible when models are fit to data and compared by an index of fit. Indices of fit are susceptible to many problems: they depend on functional assumptions, parameter estimation methods, response error, experimental design, and a host of other issues besides the accuracy of the model. In fact, when experimenters start with erroneous assumptions about parameters, a seriously wrong model can even achieve a better score on an index of fit than the model used to calculate perfect data (Birnbaum, 1973, 1974b).

Certain models cannot be distinguished in certain experimental designs; for example, there would be no point in comparing the fit of the TAX model and CPT in choices between binary gambles, because these two models are virtually identical for such cases. Similarly, these models can make almost identical predictions inside the probability simplex useful for testing EU theory, but not useful for comparing CPT and TAX (Birnbaum, 2008b). An index of fit in such cases might yield conclusions that are worse than worthless since they likely say more about the assumptions made by the analyst when tweaking models than about the true behavior of the participants.

By testing critical properties, one can evaluate models without having to make particular assumptions concerning functions and parameters. For example, CPT must satisfy SD for any choice of monotonic u(x) and W(P) functions. We need not compare logarithmic functions, power functions, exponentials or a polynomials for u(x), nor do we need to compare various parametric W(P) functions to see which combination of functions and parameters gives the “best” overall index of fit. When a participant violates SD, we know that no version of Equation 2 can “fit” this result.

Certain ideas are useful for comparing the “fit” of models with differing “flexibility” in non-experimental data. For example, one approach is to use rival models to fit half of the data and then see which model does best in predicting the other half. Another approach is to correct a model for its space of possible predictions (Davis-Stober & Brown, 2011). Although these approaches are useful, especially with limited data, they do not necessarily apply in experimental research where critical tests are possible.

For example, there would be no need to fit both TAX and CPT to half of our data and then to use these fitted models to predict the other half of the data, with the “winner” being the model that had the highest cross validation index of fit.

Because we used critical tests, the outcome of such a cross-validation contest is a foregone conclusion. We know that if people violate stochastic dominance in each half of their data (which they do) and because no CPT model can fit either half of data (since no CPT model predicts violations of SD), we know CPT cannot fit the other half of the data. Because TAX (for the tests of SD in this paper) predicts violations with a fairly wide range of parameters (Birnbaum, 2004a), it would be hard for TAX to miss. So the TAX model already “won” this contest when its “prior” parameters informed us how to design a new test that in fact yields strong violations of a critical property.

Now it may seem that critical tests, such as this test of SD, are not equally “fair” to both models because TAX can either violate or satisfy SD and CPT must satisfy it. But who said experiments can be fair? Indeed, the test of SD is a test of CPT and not a test of TAX, which was never in danger, except of having assumed a poor choice of parameters. Tests of critical properties put one class of models in danger, whereas the rival models can stand on the sidelines and watch the demolition derby. Of course, it was not a foregone conclusion that so many people would violate SD with this test, but once it has happened, we don’t need to confirm the comparison of models by cross-validation.

In contrast, when testing the critical property of transitivity of preference, both TAX and CPT are in danger and the family of lexicographic semiorder (LS) models, including PH, have the advantage that with suitable parameters, these models can predict violations of transitivity, whereas TAX and CPT (as well as other transitive models like EU, SWU, SWAU, original PT) would be refuted by systematic violations. The family of LS models are not refuted by transitive data, however, because with suitable parameters, these models can describe transitive data. So a test of transitivity is “unfair” (if we want to use such terms) to transitive models, where the LS models can describe either transitive or intransitive results, and models like TAX or CPT are in danger of refutation.

Birnbaum and Bahra (submitted) performed a series of tests designed to search for systematic violations of transitivity. Just as the TAX model’s “prior” parameters were used here to design experiments testing RBI and SD, Birnbaum and Bahra (submitted) used the PH and its parameters to design their tests of transitivity. These tests used a feature called “linked designs,” that allow one to test a family of models in which different people might have different priority orders for examining the attributes, and they were allowed to have individual differences in thresholds, where a fairly wide range of parameters would imply intransitive preferences. Only one person showed a pattern of intransitive preferences consistent with use of a LS model, but that person also violated interactive independence. No person was found by Birnbaum and Bahra (submitted) whose data satisfied the predictions of the PH.

The test of RBI is an interesting case because CPT, TAX, and PH all predict violations (but of different types) and the family of EU, SWU, SWAU, PT, and certain heuristics like toting up imply no violations. So this class of models including EU could complain that the test is not “fair,” and they could not win a cross-validation contest if both halves of the data show systematic violations of RBI (which they do).

In the case of RBI, however, CPT is the most flexible model with respect to this property because with a free W(P) function, it could predict satisfaction, or either type of violations. But CPT needs its inverse-S shaped weighting function if it plans to account for the Allais paradoxes, so CPT’s “flexibility” is limited if we also require it to predict Allais paradoxes. And the special TAX model, the form in which the amount of weight transferred is always a fixed proportion of the branch losing weight allows only one type of violation, or none. So, special TAX is less “flexible” than CPT with free parameters. Should CPT be punished for being more flexible? If one experimenter required CPT to have the inverse-S and another did not, then this same model might be declared to be of different levels of flexibility.

Because both TAX and CPT can “fit” violations of RBI, does it make sense to compare them by cross-validation from half of the RBI data to the other half? If CPT is free to choose any W(P) function, it can fit better because it can pick up not only the vast majority who showed the SR^′ pattern of violation (but using an S-shaped weighting function), it can also fit the one case who had the RS^′ pattern (with the more usual inverse-S). Does this mean that CPT should be favored by such a contest of “fit?” We say, no, because the S-shaped weighting function that would be required for the vast majority of cases has other implications that are not tested here and which could easily be tested by experiment.

In particular, choices among binary gambles show that CPT requires an inverse-S function. So the inverse-S required for binary gambles is contradicted by the S-shape required for three branch gambles (Birnbaum & Navarrete, 1998).

Instead of calculating an index of fit, and cross-validating the CPT model fit to data, which in this case might lead to victory for CPT on cross-validation (because of the one person), or trying to “correct” the fit of these models by computing flexibility, which might favor the special TAX model (because it does not allow the pattern of that one outlying case), the consistency implied by CPT can be formalized as a critical property, which we think is a more useful way to analyze the connection between these phenomena than simply fitting data to models trying to use a formula to do the thinking for us.

The critical properties in which CPT is required to have both an inverse-S function and an S-shaped function are known as upper and lower cumulative independence, which Birnbaum (1997) deduced and which Birnbaum and Navarrete (1998) tested, with the results that CPT needs both an inverse-S and S-shaped weighting functions; in other words, CPT leads to self-contradiction. Parameters played their role when we designed the study. So, using critical properties, there is no need to estimate parameters or compute an index of fit.

The case of the PH provides a good example of how conclusions based on an index of fit fall apart under deeper examination. The argument for PH over models like CPT and TAX was based on its supposedly better accuracy in “predicting” modal choices, when fit was calculated for certain previously published data (Brandstätter, et al., 2006). However, the winners and losers in the contest of fit are reversed when both PH and its rivals are allowed to estimate their parameters from the same data (Birnbaum, 2008a). The conclusions were also reversed when PH was evaluated for previously published data that had not been considered when the model was devised (e.g., Birnbaum & Navarrete, 1998).

But the most important problem for PH has been its failure to predict new results when its implications have been tested in new experiments (Birnbaum, 2008c, 2010; 2011; Fiedler, 2010; Glöckner & Betsch, 2008; Glöckner & Herbold, 2011; Hilbig, 2008, 2010, Rieskamp, 2008). The present data contribute an even stronger conclusion; namely, we found no one who conformed to the predictions of this theory, even when it is expanded to include a toolbox of other processes and free parameters, except for those cases compatible with EU, whose data might also be described by the “toting up” heuristic and not the PH.

Two recent studies have been cited as compatible with the PH. Arieli, Ben-Ami, & Rubinstein (2011) examined eye movements and found that decision makers sometimes moved their eyes as if they were comparing alternatives attribute-wise, and in other cases, moved their eyes as if they were examine attributes within an alternative. It is unclear, however, that the order in which people read in information is necessarily related to the order in which they use it. A naive view of attention is that a person must look at something in order to attend to it; however, a large body of evidence has shown that attention may be directed to different parts of a visual image, independent of where the eye fixates (see review by Sperling, Reeves, Blaser, Lu, & Weichselgartner, 2001 and papers cited there). In the days when astronomers looked through telescopes, they looked away from the objects on which they focused their attention, in order to see them better. Consequently, eye fixations do not identify unambiguously where attention is directed within a display.

Because there are multiple interpretations, we think that eye movements and related co-variables should not be naively interpreted as tests of models of decision-making. See Johnson, Schulte-Mecklenbeck, and Willemsen (2008) and Schulte-Mecklenbeck, Kühberger & Ranyard (2011) for additional discussions of evidence and issues involved.

Brandstätter and Gussmack (2012) found that people often report comparisons of attributes as “reasons” for their choices in “think-aloud” and “predict-aloud” tasks that these authors declare are not varieties of “introspection.” We find it doubtful that decision-making is mediated by language because animals make decisions without language, and because language is too slow, imprecise, and demanding to mediate important life-and-death decisions that people make, for example, while driving. Ben Franklin (1771–1788) remarked, “So convenient a thing it is to be a reasonable Creature, since it enables one to find or make a Reason for everything one has a mind to do.”

The idea of an “adaptive toolbox” that contains different strategies does not seem controversial, in our opinion. What we find odd is not what has been imagined inside the toolbox, but what has so far been excluded from it—banished without due process. Why does such a toolbox exclude addition, multiplication, and all of psychophysics?

It seems reasonable to suppose that with sufficient training, people could be trained to apply the priority heuristic. One could then test the trainees using choice problems such as used here. If training were successful, those instructed to use PH should satisfy SD and show the RS^′ pattern of violation of RBI. They should also show the predicted violations of transitivity implied by the model, and they should satisfy integrative independence, interactive independence, and priority dominance. However, people who have not yet been trained do not appear to exhibit such behavior (Birnbaum, 2010), and we consider it more important to predict what people do, rather than where they look or what they say.

7.2  Individual true and error theory

We consider that iTET provides a reasonable way to separate variability of response due to “error” from “true” violations of the model. Wilcox (2008) noted that certain theories of variability of response interact with the models to be evaluated. For example, representing error as an additive random effect attached to utility of gambles can force the implication that true preferences are transitive. That approach is therefore not well-suited for the evaluation of transitivity (Birnbaum & Schmidt, 2008). Similarly, the assumption that error rates are equal for all choice problems or for all people can make it too easy to refute EU theory, in cases where iTET would indicate that this model is acceptable.

The key idea in iTET is that preference reversals within a block of trials provide an estimate of the error rate for that person and that choice problem. The model assumes that within a block of trials, a person has a fixed set of “true” preferences. In any given block of trials, for example, the person is assumed to truly satisfy or truly violate stochastic dominance in both of the tests treated as equivalent. This model has testable implications, and in fact, it did not provide a satisfactory fit to all of the individual tests.

A rival method intended to separate the variability of response from structural inconsistency of data relative to theory is that of Regenwetter, et al. (2011). This approach requires stronger assumptions than those of iTET. It assumes that repeated responses to the same item can be treated as an independent and identically distributed sample from a theoretical mixture of true preferences. In our present SD and RBI data, we found that the observed proportions of repeated response patterns frequently exceeded the product of the marginal choice proportions, contrary to these iid assumptions.

Our data testing transitivity in linked designs (Birnbaum and Bahra, submitted) also show systematic violations of iid (see also Birnbaum, 2012). Therefore, we think that the assumption of independence and identical distribution of responses by the same person to repeated presentations of the same choice problem is not empirically descriptive. In iTET, the iid assumptions could hold if a person had a fixed set of preferences, but it appears instead that people change their true preferences during a long study.

The iTET model assumes that a person does not change true preferences within a block of trials, but only between blocks. A more realistic assumption might be that people update parameters throughout the study from trial to trial (Birnbaum, 2011), so this assumption may also be incorrect; however, we think it more realistic to assume that response patterns between blocks are independent than to assume that individual trials within blocks are independent.

References

Appendix A. Analysis of Restricted Branch Independence in CPT

Equation 2 (RDU, RSDU, and CPT) could in principle accommodate either pattern of violation of RBI when the decumulative probability weighting function is free. However, in order to account for the Allais paradoxes, these models assume an inverse-S weighting function of decumulative probability. In these models, weights are assumed to be as follows:
w₁=W(p)

w₂=W(2p)−W(p)

w₃=1−W(2p)
and in the case where the common branch has the highest consequence, z^′:
w₁^′=W(1−2p)

w₂^′=W(1−p)−W(1−2p)

w₃^′=1−W(1−p)
Birnbaum (2008b) noted that such a function satisfies, for all p < p*:
W(2p)−W(p) < W(p)−W(0) and W(1−p)−W(1−2p) < W(1)−W(1−p); that is,w₂<w₁ and w₂^′<w₃^′. It follows that
(A.1)      w₂/w₁<1<w₃^′/w₂^′.
Comparing Expression A.1 with Expressions 4 and 5, we see that CPT with any inverse-S implies that violations of RBI, if they are observed, should be of the form, R≻S and S’≻R’, denoted the RS^′ pattern. CPT with an S-shaped weighting function could not account for the Allais paradoxes but it could predict the opposite pattern of violation, and if W(P) = P, CPT reduces to EU and implies RBI. Therefore, CPT is flexible with respect to RBI, depending on its parameters.

Appendix B. Analysis of Adaptive Toolbox and Restricted Branch Independence

Brandstätter, et al. (2008) replicated a portion of a study by Birnbaum and Navarrete (1998), in which the PH had failed to predict even half of the modal choices; their replication confirmed that the PH performed worse than chance in describing their new data (Birnbaum, 2008d). In an attempt to fit their results, Brandstätter, et al. proposed that people use an “adaptive toolbox” of heuristics that precede or may circumvent the PH. In particular, they proposed that people search each choice problem for “triggering” conditions that help them decide which “tools” in the toolbox to use. Do the gambles differ in EV by a ratio exceeding 2? If so, choose the gamble with higher EV. Are the probabilities of two branches equal? If so, add their outcomes. Do two branches have the same consequences? If so, add their probabilities. Do two alternatives have common branches? If so, cancel them.

They proposed that people perform a similarity analysis in order to “search for a no-conflict solution.” Only if no decision is determined by one of these higher priority heuristics in the toolbox, do people use the PH.

This appendix shows that none of these particular heuristics accounts for the systematic SR^′ pattern that is more frequent in this study than the RS^′ pattern predicted by PH, nor do two other ways of expanding the PH model (by introducing individual threshold parameters or allowing a different order of examining the attributes) accomplish the goal of fitting these results.

Toting up heuristic

The toting up heuristic assumes that people add the consequences within each gamble and compare the sum. Suppose that people compare S = (x, y, z) and R = (x^′, y^′, z) as follows: if T(S) = u(x) + u(y) + u(z) > T(R) = u(x) + u(y) + u(z), then choose S; if T(S) < T(R), choose R; otherwise, choose randomly. To allow for individual differences, each person might have a different utility function, u(x).

Brandstätter, et al. (2006, 2008) argued against psychophysical functions, so they might not allow each person to have a different utility function. They proposed only the special case, u(x) = x, which implies that a person should choose the “risky” gamble in the first seven rows of Table 2 and in the first eight rows of Table 3, with the pattern RR^′. A person should choose the “safe” gambles in all cases in the last row of Table 2, where S = ($2, $50, $55) and R = ($2, $5, $95). Thus, the “toting up” hypothesis with u(x) = x implies that the response patterns should all be RR^′, except in the last row of Table 2, where it should be SS^′, and the person should be undecided in the last row of Table 3, where S = ($3, $48, $52) and R = ($3, $4, $96). No one fit this pattern of responses exactly, and only one person gave data even close to this predicted pattern, which is the same as EV.

If different people have different utility functions, however, then people might switch from the pattern RR^′ in the first rows to SS^′ in the last rows. For example, suppose u(x) = x^0.6. In that case, the person would switch from preferring the “risky” gambles in the first five rows of Table 2, RR^′, to SS^′ in the last three rows. As shown in Appendix D, we did not find cases that switched from RR^′, to SS^′, without showing violations of RBI.

The “toting up” heuristic, with any function u, implies RBI.

Proof:
S ≻ R ⇔ T(S) > T(R) ⇔ u(z)+u(x)+u(y) > u(z) + u(x^′) + u(y^′) ⇔ u(x) + u(y) > u(x^′) + u(y^′) ⇔ u(z^′) + u(x) + u(y) > u(z^′) + u(x^′) + u(y^′) ⇔ S^′≻ R^′

Thus, RBI is a critical test of “toting up” and systematic violations of RBI disprove this heuristic. Note that when the probabilities are equal, as in this study, “toting up” is equivalent to EU, and EV is a special case of “toting up,” where u(x) = x. Therefore, the toting up heuristic is equivalent to the EV heuristic; neither accounts for systematic violation of RBI.

Cancellation

Cancellation was proposed as an editing rule by Kahneman and Tversky (1979), who gave an example showing that it implies RBI. The idea of cancellation is that if two gambles in a choice problem have a common probability-consequence branch, the branch can be canceled. Therefore, S =(x, y, z) versus R=(x^′, y^′, z) is equivalent to S =(x, y) versus R = (x^′, y^′), which is equivalent to S = (x, y, z^′) versus R = ( x^′, y^′, z^′). Therefore, RBI is a critical test of the cancellation heuristic because anyone who uses cancellation, followed by any fixed decision rule will satisfy RBI. If people are inclined to follow cancellation, this experiment would certainly make it easy for them to do so because so many trials had common branches.

Similarity evaluation

Similarity evaluation has been discussed by Rubinstein (1988) and in a modified form by Leland (1988). Brandstätter, et al. (2008) argued for this evaluation as a prelude to the priority heuristic, even though it employs psychophysical transformation of consequences and probability. Leland’s similarity model can handle certain phenomena that have been shown to contradict CPT and the PH (Birnbaum, 2008c). In Leland’s version, the decision maker first evaluates EU, and if the difference in EU is not decisive, the decision is based on similarities evaluated on components of the gambles. EU satisfies RBI; therefore, the response pattern must be either RR^′ or SS^′ whenever EU is decisive.

If EU is not decisive, the person compares consequences and probabilities. It is assumed that when probabilities or consequences are equal they are similar and thus drop out of the process. Suppose there is a similarity function, v(x). Two versions of similarity are as follows: (1) Largest dimension difference: Choose R (S) if v (x^′) − v(x) > (<) v(y) − v(y^′) and otherwise be indecisive. Because the common consequence has been canceled, this comparison is the same in the two remainder choices, so this model implies RBI. (2) Dissimilarity threshold: Choose R (S) if v (x^′) − v(x) > d (< d) and v(y) − v(y^′) < d (> d), where d is a similarity threshold; otherwise indecisive. Either the person choosesS and S^′ or R and R^′, or is indecisive in both cases, but there is no reason why a person would systematically choose R and S^′ or S and R^′. Therefore, RBI is a critical test of either form of this similarity hypothesis, whether preceded by EU evaluation or not.

A “greatest advantage” heuristic that violates RBI is as follows: choose the gamble with the greatest consequence difference compared to the least value in the other gamble. In this case, R=($2, $5, $95) ≻ S=($2, $35, $40) because $95–$2 is the greatest advantage, and S^′=($35, $40, $98) ≻ R^′=($5, $95, $98) because $98–$5 is the greatest advantage. Like the PH, this heuristic also implies the opposite pattern of violation from the pattern more frequently observed.

One could modify the similarity heuristic as follows to produce the SR^′ pattern: Introduce a different similarity function on each ranked branch. In other words, in the choice between S and R, use u(x^′)–u(x), v(y) − v(y^′), and w(z) − w(z); in the choice between S^′ and R^′, use u(z^′) − u(z^′), v(x^′) − v(x), and w(y) − w(y^′), and map differences in value on the middle branch, v, into a larger range of values, effectively making differences in the middle ranked branch more important. With that modification, this heuristic with three similarity functions (or one function with three weights) can produce the SR^′ pattern of violation.

Priority heuristic with free parameters

According to the priority heuristic, a person starts by comparing the lowest consequences of the two gambles, and chooses a gamble when the consequences differ by more than 10% of the highest consequence. In this study, that threshold is $10; therefore, the person should always choose always choose R = ($2, $5, $95) ≻ S = ($2, x, y), because $95 − y ≥ $10 in all rows of Table 2. Similarly, S^′= (x, y, $98) ≻ R^′= ($5, $95, $98) in all rows Table 2 because x − $5 ≥ $10, so the response pattern should be RS^′ in every row.

However, suppose that different individuals have different thresholds. For example, a person with a threshold of $20 would continue to prefer R ≻ S in all rows, but would be undecided between S^′ and R^′ in the first two rows where the differences in lowest outcomes are less than $20. The response patterns in the remaining rows are RS^′. Increasing the threshold increases the number of undecided cases, where people respond randomly, but it would not produce the opposite response pattern, except by chance.

Suppose some people start with the highest consequences first and compare the lowest consequences later. Such people would still choose R ≻ S in all rows of Table 2 because the highest consequences differ by more than $40 in all cases. When comparing S^′ and R^′ the person would again choose S^′ in all cases because the highest consequences are equal and the lowest one differ by $10 or more. Increasing the threshold would again create undecided cases, but it would not produce the SR^′ response pattern, except by chance.

As noted in Birnbaum and McIntosh (1996), the theory that people compare only the middle branches (they called this heuristic “median” theory) implies the SR^′ pattern of violations in every row. Despite such evidence in the literature, however, Brandstätter, et al. (2006) proposed that people do not even consider any middle branches of gambles. The best way to improve the fit of the priority heuristic to the results of this paper would be to assume that people start by examining the middle branches of gambles. Of course, that would not solve other critical violations of the family of Lexicographic Semiorder models for properties such as interactive independence and integrative independence (Birnbaum, 2010).

Appendix C. Analysis of the RBI in the TAX model

RAM, TAX and GDU models, with their typical parameters, imply the opposite type of violation of RBI; i.e., SR^′ instead of the pattern predicted by CPT. According to the “special” TAX model, weight transfers among branches are always the same proportion of the branch losing weight. In this special TAX model, only the SR^′pattern is possible (Birnbaum, 2008b, p. 486) or the person will satisfy RBI.

In the TAX model, weight (attention) is drawn from branches leading to higher consequences to branches leading to lower consequences, leading to w₃ (the weight of the lowest branch) gaining weight at the expense of w₁. The weights in this case, where t(p) is the probability weighting function and ω ≥ 0 is the weight transfer (configural weighting) parameter, are given as follows:
(C.1a)      w₁=[t(p)(1−2ω)]/D

(C.1b)      w₂=t(p)/D

(C.1c)      w₃=[t(1−2p)+2ω t(p)]/D
where D = t(p) + t(p)+ t(1 − 2p) is the sum of the weights. Note that the highest consequence gave up ω t(p) to each of the other branches and that the middle branch gave up that amount to the lowest branch but received the same amount from the highest branch. In the choice between S^′ and R^′, the weights are as follows:
(C.2a)      w₁^′=[t(1−2p)(1−2ω)]/D

(C.2b)      w₂^′=[t(p)(1−ω)+ω t(1−2p)]/D

(C.2c)      w₃^′=[t(p)+ω t(p)+ω t(1−2p)]/D
where D is the same as in Equations C.1; it follows that
(C.3)      w₂/w₁=1/(1−2ω) > w₃^′/w₂ ^′=
[t(p)(1+ω)+ω t(1−2p)]/[t(p)(1−ω)+ω t(1−2p)]
Therefore, people should show the SR^′ pattern of violation of RBI, unless ω = 0, in which case there would be no violations.

In the case of three equally likely consequences, as in this study, condition C.3 simplifies to,
(C.4)      w₂/w₁=1/(1−2ω)>w₃^′/w₂^′=(1+2ω)/1
In the case where weight is transferred from the lowest consequences to the highest, the same relation holds because,
(C.5)      w₂/w₁ = 1/(1 + 2ω)>w₃^′/w₂^′=(1−2ω)/1
Therefore, whether weight is transferred from highest to lowest or lowest to highest, the special TAX model implies the same SR^′ pattern of violations; only when ω=0, does this model imply RBI. Birnbaum and Beeghley (1997) found this pattern in both buyer’s and seller’s prices, which are theorized to have opposite directions of weight transfer.

Appendix D: True and error analysis of RBI

There are four possible response patterns in each pair of choices (in each test): SS^′, SR^′, RS^′, and RR^′. We have the following for the probabilities of observing each response pattern:
(D.1a) p(SS^′)=p_SS^′(1−e)(1−e^′)+
p_SR^′(1−e)e^′+p_RS^′ e(1−e^′)+p_RR^′ee^′
(D.1b) p(SR^′)=p_SS^′(1−e)e^′+
p_SR^′(1−e)(1−e^′)+p_RS^′ee^′+ p_RR^′e(1−e^′)
(D.1c) p(RS^′)=p_SS^′e(1−e^′)+
p_SR^′ee^′+p_RS^′(1−e)(1−e^′)+p_RR^′(1−e)e^′
(D.1d) p(RR^′)=p_SS^′ee^′+p_SR^′e(1−e^′)+
p_RS^′(1−e)e^′+p_RR^′(1−e)(1−e^′)
where p_SS^′, p_SR^′, p_RS^′, and p_RR^′ are the “true” probabilities of each response pattern in a block of trials (which sum to 1), e and e^′ are the error rates in the two choice problems; these are assumed to be independent and less than ½. The assumption of RBI is the assumption that p_SR^′ = p_RS^′ = 0.

Because each choice problem is presented twice in each block, we can estimate the error rates from preference reversals within blocks, p(SR) = p(RS) = (1 − e)e. For the two choice problems testing S versus R, we have:
(D.2a) p(SR)+p(RS)=2(1−e)e
(D.2b) p(SS)=(p_SS^′+p_SR^′)(1−e)²+(p_RS^′+p_RR^′)e²
(D.2c) p(RR)=(p_RS^′+p_RR^′)(1−e)² + (p_SS^′+p_SR^′)e²
where p(SS) is the probability that the person selected the response S in both choices between S and R in a block; p_S = 1 − p_R = p_SS^′ + p_SR^′; p_R = p_RS^′ + p_RR^′ and e is the error term in the choice between S and R. Expressions D.2 involve no additional parameters beyond those in Expressions D.1.

The preference reversals in the two choices between S^′ and R^′ can also be used to estimate the error rate in this choice because p(S^′R^′) = p(R^′S^′) = (1 − e^′) e^′, where e^′ is the error rate in this choice.
(D.3a) p(S^′R^′)+p(R^′S^′)=2(1−e^′)e^′
(D.3b) p(S^′S^′)=(p_SS^′+p_RS^′)(1−e^′)² +
(p_SR^′+p_RR^′)(e^′)²
(D.3c) p(R^′R^′) = (p_SR^′ + p_RR^′)(1 − e^′)² +
(p_SS^′ + p_RS^′)(e^′)²
In addition, because each pair of choice problems is presented twice within each block, there are 16 possible, 4 choice, response patterns within each block. In particular, we can analyze the probabilities of repeating each choice pattern on both tests in a block:
(D.4a) p(SS^′, SS^′)=p_SS^′(1−e)²(1−e^′)²+
p_SR^′(1−e)² (e^′)²+ p_RS^′e² (1−e^′)²+p_RR^′e²(e^′)²
(D.4b) p(SR^′, SR^′)=p_SS^′(1−e)²(e^′)² +
p_SR^′(1−e)²(1−e^′)²+ p_RS^′e²(e^′)²+p_RR^′e²(1−e^′)²
(D.4c) p(RS^′, RS^′)= p_SS^′e²(1−e^′)² + p_SR^′e²(e^′)² + p_RS^′(1−e)²(1−e^′)² + p_RR^′(1−e)²(e^′)²
(D.4d) p(RR^′, RR^′)= p_SS^′e²(e^′)² + p_SR^′e²(1−e^′)² + p_RS^′(1−e)²(e^′)² + p_RR^′(1−e)²(1−e^′)²
where p(SR^′, SR^′) is the probability of showing the same SR^′ response pattern on both tests of RBI within a block. These probabilities in Expressions D.4 are the same as those in Expressions D.1, except that each of the components involving error terms are squared; these four terms do not sum to 1.⁶

The assumption that RBI is satisfied corresponds to the assumption that p_SR^′ = p_RS^′=0, which means that p_RR^′ = 1 − p_SS^′. If so, the probability of showing a repeated violation of the type predicted by the TAX model is p(SR^′, SR^′) = p_SS^′ (1 − e)² (e^′)² + p_RR^′ e² (1 − e^′)². It follows that the maximal rate of showing two violations of this type in a block is 0.0625. If a person completed 20 blocks and showed 4 blocks in which a particular violation (i.e., SR^′) is repeated, we can reject the hypothesis that p_SR^′ = 0, because the binomial probability to show 4 or more repeated SR^′ violations in 20 blocks is only .033. This upper bound follows from the conservative assumption that errors cannot exceed ½.

We can impose a still smaller upper bound by estimating the error terms using preference reversals to each type of choice problem to, as in the previous section. Suppose we find 32% preference reversals for both S versus R and S^′ versus R^′; it follows that e = e^′= 0.2; therefore, the maximal rate of repeated violations of one type is 0.0256, if RBI holds. In this case, 3 repeated SR^′ violations out of 20 blocks would suffice to reject the hypothesis that p_SR^′ = 0, since the binomial probability to show 3 or more out of 20 with p=.0256 is only .014.

We can again explore independence, which is the assumption that the probability of any response combination is the product of the marginal probabilities of the components; for example, p(SR^′) = p(S) p(R^′) and p(SR^′, SR^′) = p(S)² p(R^′)². Independence does not follow from the iTET model unless one of the four “true” probabilities of a response combination is 1; for example, if p_SR^′=1. If a person changed “true” preferences from block to block, as might be expected under CPT or TAX if a person’s parameters changed from block to block, for example, then independence will be violated. Again, the probability of a repeated pattern that is “real” but imperfect will exceed the product of the marginal probabilities according to iTET.

There are 16 equations in Expressions D.1 through D.4 that express predictions of iTET for probabilities of response patterns. One can estimate five parameters in order to fit the 16 observed proportions corresponding to these expressions: e, e^′, p_SS^′, p_SR^′, p_RS^′, and p_RR^′ = 1 − p_SS^′ − p_SR^′ − p_RS^′. The models of risky decision making to be compared are then special cases of iTET: the prior TAX model implies p_SR^′ > 0; CPT with an inverse-S weighting function and PH imply instead that p_RS^′ > 0; EU and SWU (including original prospect theory) imply RBI, which means that p_SR^′ = p_RS^′=0.

True and error analysis of RBI: Results

In Study 2, the two RBI designs were intermixed in the same blocks; this procedure allows us to apply iTET to each person’s data. The tests in Row 5 of Table 2 [S = ($2, $35, $40), R = ($2, $5, $95), S^′ = ($35, $40, $98), R^′ = ($5, $95, $98)] and Row 5 of Table 3 [S = ($3, $36, $40), R = ($3, $4, $96), S^′ = ($36, $40, $97), R^′ = ($4, $96, $97)] were treated as equivalent. These two choice problems also counterbalanced position, so to repeat the same response pattern on both tests, a participant would have to press opposite buttons appropriately on four trials.

In the same fashion, Rows 1 & 1, 3 & 2, 4 & 3, 6 & 6, 7 & 8, and 8 & 9 (in Tables 2 and 3, respectively) were paired to create a total of seven tests of RBI for each of the 59 participants in Study 2, making 413 tests. The model has five parameters per test: e, e^′, p_SS^′, p_SR^′, p_RS^′, and p_RR^′ = 1 − p_SS^′ − p_SR^′ − p_RS^′. Each test for each person was fit separately to iTET to minimize the sum of squared differences between the 16 predicted and obtained proportions corresponding to the probabilities in Equations D.1 through D.4.

The results of the seven tests for participant #216 are shown in Table D.1. Parameter estimates are listed in the last six rows. Note that in the first test (first row of Table 2), this person was estimated to have had a perfect true preference for R and R^′; i.e., p_RR^′ = 1. As the “safe” gambles are improved, p_RR^′ decreased to zero and is replaced in the last four columns by perfect adherence to the SR^′ pattern of violation of RBI.

---

Table D.1. Observed choice proportions and estimated parameters of the individual true and error model in seven tests of RBI for participant #216, who completed 21 blocks. Tests are numbered according to the row number in Table 2.

	Tests
	1	3	4	5	6	7	8
P (SS)	0.00	0.52	0.86	0.76	0.95	1.00	0.95
P (SR)	0.10	0.05	0.05	0.14	0.05	0.00	0.05
P (RS)	0.00	0.14	0.05	0.10	0.00	0.00	0.00
P (RR)	0.90	0.29	0.05	0.00	0.00	0.00	0.00
P (S′S′)	0.00	0.00	0.00	0.00	0.00	0.00	0.00
P (S′R′)	0.00	0.00	0.00	0.00	0.05	0.00	0.00
P (R′S′)	0.00	0.00	0.00	0.00	0.05	0.00	0.00
P (R′R′)	1.00	1.00	1.00	1.00	0.90	1.00	1.00
P (SS′)	0.00	0.00	0.00	0.00	0.05	0.00	0.00
P (SR′)	0.05	0.62	0.90	0.88	0.93	1.00	0.98
P (RS′)	0.00	0.00	0.00	0.00	0.00	0.00	0.00
P (RR′)	0.95	0.38	0.10	0.12	0.02	0.00	0.02
P (S S′, S S′)	0.00	0.00	0.00	0.00	0.00	0.00	0.00
P (S R′, S R′)	0.00	0.52	0.86	0.76	0.86	1.00	0.95
P (R S′, R S′)	0.00	0.00	0.00	0.00	0.00	0.00	0.00
P (R R′, R R′)	0.90	0.29	0.05	0.00	0.00	0.00	0.00
e	0.05	0.11	0.05	0.13	0.03	0.00	0.02
e′	0.00	0.00	0.00	0.00	0.05	0.00	0.00
pSS′	0.00	0.00	0.00	0.00	0.00	0.00	0.00
pSR′	0.00	0.65	0.95	1.00	1.00	1.00	1.00
pRS′	0.00	0.00	0.00	0.00	0.00	0.00	0.00
pRR′	1.00	0.35	0.05	0.00	0.00	0.00	0.00

---

Results for participant #234 are shown in Table D.2, as in Table D.1. This person’s data for the first two columns (Tests 1 and 3) do not fit iTET. Note that P (SR ) = 0.53 > P (RS ) = 0.05. The estimated error terms for these two tests are also relatively large and unequal. Nevertheless, the results for Tests 4–8 appear to fit the model and provide reasonable parameter estimates.

---

Table D.2. Observed choice proportions and estimated parameters of the individual true and error model in seven tests of RBI for participant #234, who completed 19 blocks, as in Table D.1.

	Tests
	1	3	4	5	6	7	8
P (SS )	0.00	0.42	0.53	0.79	0.89	0.79	0.89
P (SR )	0.53	0.11	0.11	0.05	0.05	0.05	0.05
P (RS )	0.05	0.37	0.21	0.11	0.05	0.16	0.05
P (RR )	0.42	0.11	0.16	0.05	0.00	0.00	0.00
P (S′S′)	0.00	0.05	0.05	0.16	0.11	0.16	0.26
P (S′R′)	0.05	0.00	0.11	0.05	0.05	0.05	0.26
P (R′S′)	0.05	0.11	0.21	0.11	0.16	0.05	0.05
P (R′R′)	0.89	0.84	0.63	0.68	0.68	0.74	0.42
P (SS′)	0.03	0.11	0.16	0.21	0.18	0.18	0.39
P (SR′)	0.26	0.55	0.53	0.66	0.76	0.71	0.55
P (RS′)	0.03	0.00	0.05	0.03	0.03	0.03	0.03
P (RR′)	0.68	0.34	0.26	0.11	0.03	0.08	0.03
P (S S′, S S′)	0.00	0.05	0.00	0.11	0.11	0.16	0.21
P (S R′, S R′)	0.00	0.37	0.26	0.53	0.63	0.63	0.37
P (R S′, R S′)	0.00	0.00	0.00	0.00	0.00	0.00	0.00
P (R R′, R R′)	0.42	0.11	0.11	0.05	0.00	0.00	0.00
e	0.31	0.35	0.21	0.09	0.05	0.10	0.06
e′	0.06	0.05	0.21	0.09	0.11	0.04	0.20
pSS′	0.00	0.07	0.02	0.17	0.11	0.18	0.36
pSR′	0.00	0.91	0.78	0.77	0.88	0.82	0.64
pRS′	0.00	0.00	0.00	0.00	0.01	0.00	0.00
pRR′	1.00	0.02	0.21	0.06	0.00	0.00	0.00

---

Examining tables corresponding to Tables D.1 (and D.4) for each of the 59 participants, we found the majority showed two common trends: most people showed evidence of the SR^′ pattern of violation of RBI and most showed either decreasing p_RR^′or increasing p_SS^′ (or both) as the values of (x, y) increased.

Over all 413 tests, the mean estimated error terms, e and e^′ were 0.07 and 0.07, with 88% of the estimated error terms less than 0.2 and 94% less than 0.3. Slightly more than half of all estimated error terms were 0. These error terms are smaller than those estimated in the tests of SD. Perhaps the lower error rates occur because the choice problems testing RBI are simpler than those testing SD: In this analysis, they all have three equally likely consequences without probabilities to read or to process.

Of the 413 tests, 171 cases had estimated p_SR^′ > 0.2 including 72 for which p_SR^′ > .9, whereas in only 9 cases, estimated p_RS^′ > 0.2, all from just three participants. Summed over seven tests for each person, 49 of 59 participants had Σ p_SR^′ > Σ p_RS; only one person (#241) had the opposite relation, and there were 9 people who showed a difference of zero. These 9 might be candidates for EU (or another model that implies RBI, such as PT); however, 4 of these 9 had p_RR^′=1 in all seven tests, 4 had p_SS^′=1 in all seven tests, and one had p_SS^′ > 0.85 in all tests; therefore, these cases that satisfied RBI could be better described as “moot”, or “untested” by the design.

Appendix E. Individual tests of restricted branch independence

Table E.1 shows the number of response patterns for each individual, summed over the tests of restricted branch independence. RBI is implied by EU, SWU, SWAU, original PT, cancellation, toting up, and two similarity models in Appendix B. It should be violated with the pattern RS^′ according to CPT with an inverse-S weighting function and by PH. The special TAX model implies the pattern SR^′, as long as ω is not zero, and implies RBI when ω = 0. Random responding does not imply violations, except by chance.

Cases where one type of violation is significantly more frequent than the other are shown in bold. For cases where the sum of violations was less than 25, the binomial distribution was used, and in other cases, the z-test was performed. Most participants show significantly more violations of the type SR^′, predicted by TAX than of RS^′, predicted by CPT and PH. Only one person shows significantly more violations of the RS^′ type, but that person also systematically violated SD, contrary to both CPT and PH.

---

Table E.1. Summary of individual tests of restricted branch independence, summed across tests. Cases numbered 101–143 are from Study 1 and cases starting at 201 from Study 2. Bold entries show significant differences between SR^′ and RS^′ patterns, with α = .05.

Case No.	SS′	SR′	RS′	RR′	SUM
101	163	7	0	0	170
102	21	80	0	18	119
103	0	0	0	170	170
104	0	36	0	65	101
105	1	4	0	216	221
106	0	27	0	91	118
107	38	48	1	15	102
108	26	86	0	6	118
109	6	76	1	19	102
110	0	3	0	211	214
111	5	180	0	1	186
112	1	19	0	81	101
113	9	111	2	55	177
114	15	70	1	23	109
115	139	2	5	16	162
116	1	170	0	7	178
117	30	49	6	84	169
118	36	4	4	49	93
119	143	1	0	0	144
120	101	0	0	0	101
121	0	5	1	79	85
122	0	14	2	85	101
123	235	2	1	0	238

Continued on next page.

---

---

Table E.1, continued.

Case No.	SS′	SR′	RS′	RR′	SUM
124	11	93	0	6	110
125	144	82	0	3	229
126	36	64	0	17	117
127	12	93	0	39	144
128	3	142	0	16	161
129	73	59	0	2	134
130	34	39	9	11	93
131	6	85	2	8	101
132	22	8	0	97	127
133	180	14	1	0	195
134	145	13	2	1	161
135	80	40	16	8	144
136	20	36	10	27	93
137	2	19	0	183	204
138	95	2	2	2	101
139	1	109	0	0	110
140	0	0	0	246	246
141	0	3	0	201	204
142	27	91	0	0	118
143	2	42	0	58	102
201	119	57	2	9	187
202	0	44	1	210	255
203	76	11	10	22	119
204	5	240	0	27	272
205	88	11	1	2	102
206	3	24	1	125	153
207	108	20	1	24	153
208	131	5	0	0	136
209	2	103	0	116	221
210	0	23	0	11	34
211	0	9	2	142	153
212	114	7	4	28	153
213	2	88	3	94	187
214	29	11	3	42	85
215	0	14	1	257	272
216	2	270	0	85	357
217	2	21	0	62	85
218	8	5	3	103	119
219	198	4	2	0	204
220	15	119	0	2	136

---

---

Table E.1, continued.

Case No.	SS′	SR′	RS′	RR′	SUM
220	15	119	0	2	136
221	3	104	0	29	136
222	21	127	3	18	169
223	95	39	5	14	153
224	141	102	1	11	255
225	32	70	14	122	238
226	198	18	5	0	221
227	27	86	26	116	255
228	93	7	1	1	102
229	169	1	0	0	170
230	103	8	7	1	119
231	2	84	0	50	136
232	391	0	0	0	391
233	61	120	0	6	187
234	58	185	10	70	323
235	1	16	1	50	68
236	14	138	1	0	153
237	116	127	8	38	289
238	51	29	0	5	85
239	9	61	3	63	136
240	40	190	0	25	255
241	66	1	149	39	255
242	0	0	4	115	119
243	3	154	1	63	221
244	0	0	0	204	204
245	7	9	4	184	204
246	12	15	12	12	51
247	83	129	3	6	221
248	11	29	7	259	306
249	181	6	0	0	187
250	20	28	0	3	51
251	82	97	28	48	255
252	0	0	1	118	119
253	29	16	7	84	136
254	24	27	1	16	68
255	2	20	4	127	153
256	0	3	3	266	272
257	0	11	2	344	357
258	19	46	2	1	68
259	68	6	3	8	85

---

*

Department of Psychology, California State University, Fullerton, CSUF H-830M, Box 6846, Fullerton, CA 92834–6846, USA. Email: mbirnbaum@fullerton.edu.

#

Department of Psychology, California State University, Fullerton

1

One could improve the median model by averaging median and midpoint, as in range-frequency theory (Parducci, 1995).

2

There were 8 out of 102 people who showed a difference of zero between SR^′ and RS^′; however, in 7 of these 8 cases all or almost all of the response patterns were either SS^′ or RR^′. Although such cases do not violate SWU, SWAU, and PT, these models have not really been tested by the RBI designs in these 8 cases. These models imply that a person would switch from RR^′ to SS^′ as (x, y) is increased (in Table 2 or 3), but these cases do not show the switch.

3

The estimated error rate was uncorrelated with the number of blocks completed, r = 0.05.

4

Independence was tested by comparing the choice proportion repeating the SR^′ pattern, P(SR^′, SR^′), with the product of the constituent marginal proportions. The iTET model implies that the conjunction will be more frequent than predicted by independence when a response pattern is “real” but not perfect; e.g., when 0 < p_SR^′ < 1. According to independence, the difference, P(SR^′, SR^′) − P(S) P(R^′) P(S) P (R^′), should be equally likely to be positive or negative. Instead this difference was more often positive than negative; the frequencies of positive and negative differences were (13, 11), (24, 8), (21, 6), (26, 6), (24, 11), (28, 4), and (22, 8) in tests corresponding to Rows 1, 3, 4, 5, 6, 7, and 8 (of Tables 1), respectively. All except the first are significant (z = 0.41, 2.83, 2.89, 3.54, 2.20, 4.24, and 2.56, respectively).

5

To search for systematic effects of trial blocks, we compared the modal response pattern in the first and last blocks for each participant in Study 2. There were 21, 19, and 19 who showed the SS^′, SR^′, and RR^′ patterns most often on the first block. Of the 21 who began with the SS^′ pattern, 14 ended on that pattern, 4 shifted to the SR^′ pattern, and 1 to the RS^′ pattern on the last block. Of the 19 who began with the RR^′ pattern, 14 ended with the same pattern, 2 switched to SS^′, 2 switched to SR^′ and 1 to RS^′; of the 19 who started on the SR^′ pattern, 10 ended on that pattern, 4 switched to SS^′ and 5 to RR^′. Other comparisons of first and tenth, and third and last trial blocks showed the same picture; namely, about an equal number of people switched in different directions so that the marginal distributions of response patterns did not show a systematic trend.

6

It may be helpful to keep in mind that because e < 1/2, it follows that ee < e(1 − e) < (1 − e)(1 − e); for example, with e=.2, these three terms are .04, .16, and .64, respectively; the corresponding squared terms are even smaller.

This document was translated from L^AT_EX by H^EV^EA.