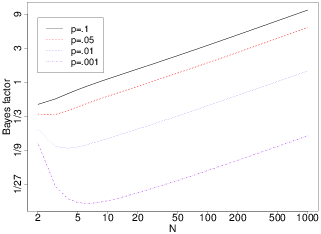
| Figure 1: JZS Bayes factor as a function of sample size for various p-values. |
Judgment and Decision Making, vol. 6, no. 8, December 2011, pp. 843-856
What might judgment and decision making research be like if we took a Bayesian approach to hypothesis testing?William J. Matthews* |
Judgment and decision making research overwhelmingly uses null hypothesis significance testing as the basis for statistical inference. This article examines an alternative, Bayesian approach which emphasizes the choice between two competing hypotheses and quantifies the balance of evidence provided by the data—one consequence of which is that experimental results may be taken to strongly favour the null hypothesis. We apply a recently-developed “Bayesian t-test” to existing studies of the anchoring effect in judgment, and examine how the change in approach affects both the tone of hypothesis testing and the substantive conclusions that one draws. We compare the Bayesian approach with Fisherian and Neyman-Pearson testing, examining its relationship to conventional p-values, the influence of effect size, and the importance of prior beliefs about the likely state of nature. The results give a sense of how Bayesian hypothesis testing might be applied to judgment and decision making research, and of both the advantages and challenges that a shift to this approach would entail.
Keywords: Null hypothesis significance testing; Bayesian inference; Bayes factor; Anchoring
In null hypothesis significance testing (NHST) we summarize the data with a test statistic and determine the probability, p, of obtaining a test statistic which is at least as extreme as the one observed if the null hypothesis H0 is true. A low p-value is taken to indicate that the null hypothesis is unlikely to be true; either H0 is false or a very improbable event has occurred. NHST has many detractors (e.g., Bakan, 1966; Nickerson, 2000; Wagenmakers, 2007), and various approaches to inference have been offered as alternatives, including an increased focus on effect sizes and confidence intervals (e.g., Cumming & Finch, 2005), and greater emphasis on replicability (e.g., Iverson, Lee, & Wagenmakers, 2009; Killeen, 2005; Miller, 2009). Perhaps the most comprehensive (and radical) alternative to NHST is the adoption of a Bayesian approach to hypothesis testing, and a number of researchers have recently argued for a more widespread adoption of this approach (e.g., Dienes, 2011; Lee & Wagenmakers, 2005; Rouder, Speckman, Sun, Morey, & Iverson, 2009; Wagenmakers, 2007; Wagenmakers, Lodewyckx, Kuriyal, & Grasman, 2010). While many judgment and decision making (JDM) researchers will be familiar with Bayesian techniques for model fitting and parameter estimation (e.g., van Ravenzwaaij, Dutilh, & Wagenmakers, 2011), hypothesis testing is overwhelmingly conducted in the NHST framework. This article begins by introducing Bayesian hypothesis testing and applying it to existing work on judgment and decision making. We then consider some aspects of this approach in more detail.
Suppose we have two competing hypotheses, the null H0 and the alternative H1, which, in advance of data collection, have probabilities Pr(H0) and Pr(H1). Because these probabilities are specified in advance of the data they are referred to as prior probabilities, and the ratio Pr(H0)/Pr(H1) constitutes the prior odds. In many cases we have no a priori reason to favour one hypothesis over the other, and the prior odds are set to 1.
We collect a set of data D. The probability of the null hypothesis given the observed data is written Pr(H0|D); the corresponding probability for the alternative hypothesis is Pr(H1|D). Because Pr(H0|D) and Pr(H1|D) are conditional on the data, they are referred to as the posterior probabilities, and their ratio gives the posterior odds:
| Ω = |
|
The posterior odds provide a natural way to choose between the hypotheses. For example, if Ω = 15 then the null hypothesis is 15 times more likely than the alternative, given the data. From Bayes’ theorem, the relationship between the posterior odds and the prior odds is given by:
| = |
| × |
|
Here Pr(D|H0) and Pr(D|H1) are the probabilities of obtaining the observed data if the null and alternative hypotheses are true, and the ratio Pr(D|H0)/Pr(D|H1) is the Bayes factor, BF01. The Bayes factor quantifies the change from prior odds to posterior odds: as such, it represents the evidence provided by the data (Kass & Raftery, 1995).
A hypothesis H will typically have a set of free parameters θ, and the probability of obtaining the observed data for a given set of parameter values is the likelihood, f(D|θ). In advance of data collection, we assign each possible parameter value a prior probability by specifying a density function p(θ|H). The choice of this prior distribution is at our disposal; it may be based on subjective beliefs about the likelihood of different parameter values, or it may be selected to be minimally informative—for example, by letting every possible parameter value be equally likely. In order to obtain the overall probability of obtaining the observed data under the hypothesis, we weight each likelihood by the corresponding prior probability of the parameters and integrate over the parameter space. This gives the marginal likelihood:
| Pr(D|H) = | ∫ | f(D|θ)p(θ|H)dθ |
The Bayes factor BF01 is the ratio of the marginal likelihoods for H0 and H1. If the hypotheses are equally probably a priori, and if we have only two hypotheses, then the Bayes factor is equal to the posterior odds, and the posterior probability of the null hypothesis Pr(H0|D) is simply BF01/(1+BF01).
This article explores what judgment and decision making (JDM) research might look like if we took a Bayesian approach to hypothesis testing. Bayesian hypothesis testing is often difficult because the integration over the parameter space required to calculate the marginal likelihoods can require Markov Chain Monte Carlo (MCMC) simulation (e.g., Kass & Raftery, 1995). However, there has been increasing emphasis on making these methods more accessible to a general audience, and on deriving analytic expressions which permit Bayesian alternatives to conventional statistical tests. We will make use of one such technique, the Jeffreys-Zellner-Siow (JZS) Bayesian t-test developed by Rouder et al. (2009). This test provides an alternative to one- and two-sample t-tests and computes the Bayes factor from the sample size and t-statistic. As described above, Bayesian hypothesis testing requires the specification of a prior distribution for the parameters of the competing hypotheses; the JZS t-test uses a Cauchy prior distribution on effect size and a Jeffreys prior on population variance, a combination referred to as the Jeffreys-Zellner-Siow (JZS) prior (Rouder et al., 2009). This amounts to a particular instantiation of the idea that the prior distribution for effect sizes is symmetrical about zero, with small effects being more probable than large ones. Mathematical details are given in the Appendix. An on-line program implementing the JZS t-test is available from http://pcl.missouri.edu/bayesfactor and an R code implementation is available from the current author.
The JZS t-test is a straightforward Bayesian alternative to a widely-used test, and its implementation conveys a sense of what judgment and decision making research might look like if the community adopted Bayesian hypothesis testing. We begin by applying the test to a number of existing studies from one important area of JDM research: anchoring.
Tversky and Kahneman (1974) proposed the anchor-and-adjust heuristic as one strategy for judgment under uncertainty. The idea is that people select a starting anchor value and then adjust towards the target quantity. The adjustments are insufficient so that judgments are biased towards the anchor (although it seems that this is not always the mechanism—see Epley and Gilovich, 2001, 2005). Anchoring has been demonstrated (or invoked as an explanation) in a huge array of judgment tasks, including legal decisions (e.g., Chapman & Bornstein, 1996; Englich & Mussweiler, 2001), choices between gambles (Carlson, 1990), house and consumer product price estimation (Matthews & Stewart, 2009; Northcraft & Neale, 1987), purchase quantity decisions (Wansink, Kent, & Hoch, 1998), valuation of pain (Ariely, Loewenstein, & Prelec, 2003), predictions of political outcomes (Chapman & Johnson, 1999), subjective confidence judgments (Block & Harper, 1991), general knowledge (Jacowitz & Kahneman, 1995), perceptual judgments (LeBoeuf & Shafir, 2006), auditing (Butler, 1986), performance evaluations (Thorsteinson, Breier, Atwell, Hamilton, & Privette, 2008) and judgments of self-efficacy (Cervone & Peake, 1986).
The breadth of interest in anchoring means that the statistical practices that guide inference about the phenomenon are of considerable importance. Here we examine the consequences of a move to Bayesian hypothesis testing on three published studies of anchoring.
Jacowitz and Kahneman (1995) asked participants to estimate quantities such as the length of the Mississippi river. A calibration group produced unanchored judgments; a test group judged whether each target quantity was lower or higher than an anchor value, with low and high anchors chosen by selecting the 15th and 85th percentiles of the calibration group. After answering the comparative question, participants estimated the target quantity and rated their confidence on a 10-point scale.
Jacowitz and Kahneman (1995) found a sizeable anchoring effect: the median subject’s judgment moved about half way to the anchor from what it would have been without an anchor. More importantly, Jacowitz and Kahneman compared confidence levels for participants provided with an anchor (either high or low) with those for participants who were not. Confidence was higher in the anchored group (N=103, M = 3.85) than in the unanchored calibration group (N=53, M=2.99). Jacowitz and Kahneman report that this difference is significant, t(154)=3.53, p<.001 (p=.00055 to 5 d.p.).
When the t and N values are supplied to the JZS t-test, the Bayes factor B01=0.0235. This means that the data are 1/0.0235=42 times more likely under the alternative hypothesis than under the null. Arguably we should leave things at that; the Bayes factor is directly interpretable as an odds ratio and there is no need for “thresholds” or “cut-offs” of the type found in NHST. However, some authors have suggested broad categories for Bayes factors; those offered by Raftery (1995) are shown in Table 1. According to this scheme, the data provide “strong” evidence in favour of the alternative hypothesis. We might also calculate the posterior probability of the null, Pr(H0|D) as 0.0235/1.0235=.023 (assuming H0 and H1 were equally probable a priori). The posterior probability of the alternative hypothesis is 1−.023=.977.
This example represents a case where the Bayesian approach yields much the same conclusion as null hypothesis significance testing. What has changed is the complexion that the analysis puts on the data. We are no longer looking for categorical yes/no decisions, but at the strength of the evidence for/against the null and alternative hypotheses.
In the “standard” anchoring paradigm, participants compare the target quantity to an experimenter-provided anchor before making their estimate. The resulting bias seems to be due to activation of anchor-consistent knowledge during the comparative judgment (e.g., Mussweiler & Strack, 1999). Epley and Gilovich (2005) theorized that accuracy incentives will have no effect on this type of anchoring because the knowledge-priming that underlies the bias is automatic. They divided participants into two groups: one received financial incentives for accuracy, the other did not. Responses were standardized and coded such that larger values meant judgments further from the anchor. A t-test indicated that the means were not significantly affected by incentive, which Epley and Gilovich report as t<1, ns.
This is a case where the researchers would like to gain evidence for the null. The lack of a significant result in NHST is couched as a failure to find an effect, and the nagging suspicion is often that there is an effect, but that the experiment failed to detect it. The odds ratio provided by the Bayesian approach allows one to assert that the data favoured (perhaps strongly) the null hypothesis. For Epley and Gilovich’s (2005) experiment, the Bayes factor B01=3.06 (assuming t=1 and that the 51 participants were split 25-26 between the incentive and no-incentive groups), meaning that the data are at least 3 times as likely under the null as under the alternative. Thus, the data provide “positive” evidence for the (theoretically important) idea that there is no effect of incentive when anchors are provided by the experimenter.
Critcher and Gilovich (2008) were interested in whether incidental values might serve as anchors. Participants read about a college linebacker, Stan Fischer. The description was accompanied by a photo of Fischer wearing a jersey bearing number 54 (low anchor condition, N=138) or 94 (high anchor condition, N=124). No special emphasis was placed on the picture or the jersey, but participants in the high anchor condition judged Fischer more likely to “register a sack in the conference playoff game” than those in the low anchor condition (mean probability judgments 61.6%, SD = 22.2%, and 55.6%, SD=25.0%, respectively). A two-sample t-test indicates a significant effect of Stan Fischer’s jersey on people’s judgments, t(260)=2.052, p=.041.1
The JZS Bayes factor for these data is 1.34 and (assuming that H0 and H1 were equally likely a priori) the posterior probability of the null Pr(H0|D)=.57. That is, the data weakly favour the null hypothesis, despite the significant result. This illustrates a key point: NHST may reject the null despite a reasonable alternative hypothesis being even more unlikely, reflecting a bias against the null discussed below. This example represents a case where different substantive conclusions are drawn from Bayesian hypothesis testing and NHST.
These examples illustrate how one easy-to-use tool for Bayesian hypothesis testing might be applied to JDM research, and what the resulting analyses might look like. We now consider some aspects of the Bayes factor approach in more detail, starting with a brief comparison with two dominant alternatives: Fisherian inductive inference and Neyman-Pearson inductive behaviour.
In Fischer’s approach to inductive inference, the researcher determines the probability under the null of obtaining a test statistic at least as extreme as the one actually observed (e.g., Fisher, 1970). This p-value is taken as a measure of evidence against the null: a small p-value indicates that either the null is false or a very rare event has occurred. p-values less than .05 are often deemed “significant”. A key feature of Fisher’s approach is that it is concerned with only one hypothesis, and “Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.” (Fisher, 1960, p. 16).
The advantage of the Fisherian approach is that it obviates the need to specify a precise alternative to the null. However, advocates of Bayesian hypothesis testing argue that it has a number of advantages over Fisher’s approach.
1. The Bayes factor provides a better measure of evidence. A Bayes factor of 5 means that the data are five times more likely under the null than under the alternative. By contrast, the relationship between p-values and evidence is unclear. Do two experiments with the same p-value but different sample sizes provide equal evidence, as Fisher seems to have thought (Wagenmakers, 2007)? Does the one with the smaller N provide more evidence (because the effect must be larger, e.g., Bakan, 1966) or the one with the larger sample size (because more data are more compelling, e.g., Rosenthal & Gaito, 1963)?
2. Fisher’s approach requires precise specification of the sampling plan before data collection. Researchers frequently violate this by “optionally stopping” (collecting additional data after a first sample fails to produce a significant result, or terminating an experiment early if a “sneak peek” reveals that significance has already been achieved; see Botella, Ximénez, Revuelta, & Suero, 2006; Frick, 1998). In the Bayesian approach, researchers may inspect the data and terminate the experiment whenever they wish. Bayesian inference obeys the likelihood principle: the conclusions drawn depend only on the data that were actually collected, not on the sampling plan that led to those observations nor on other data that might have been observed but were not (see Edwards, Lindman, Savage, 1963; Lee, 1997, Chapter 7).
3. The Fisherian approach allows us to reject the null hypothesis but never to conclude that it is true. As the APA task force on statistical inference dictate, one should “Never use the unfortunate expression ‘accept the null hypothesis’ ” (Wilkinson et al., 1999, p. 599). However, researchers often seek to establish a theoretically-important invariance—not least when arguing against an effect that has already been reported (e.g., Acker, 2008; Calvillo & Penaloza, 2009; Thorsteinson & Withrow, 2009). As Bakan (1966, pp. 427–428) notes: “even the strict repetition of an experiment and not getting significance in the same way does not speak against the result already reported in the literature. For failing to get significance …only means that that experiment is inconclusive; whereas the study already reported in the literature, with a low p-value, is regarded as conclusive.” If the null is false, increasing the sample size increases the chance of rejecting the null. However, if the null hypothesis is true, the p-value is uniformly distributed between 0 and 1 and does not depend on sample size: the null will still be rejected with probability .05. One cannot collect more data to gain evidence for the null, and Fisher’s approach tends to overstate the evidence against it (see e.g., Rouder et al., 2009). By contrast, Bayesian hypothesis testing may lead to the conclusion that the null is much more likely than the alternative hypothesis of an effect size drawn from a distribution of plausible values.
This last point is illustrated in Figure 1, which plots the change in JZS Bayes factor as a function of increasing sample size for four different p-values. For small p, increasing the sample size initially strengthens the case for the alternative hypothesis, but as sample size grows the balance shifts to the null. One striking fact is that, with a p-value of .05, the Bayes factor is only less than 1.0 for relatively small sample sizes; once N is 27 or greater, a p-value of .05 means that, assuming the JZS prior, the balance of evidence favours the null. Similarly, it is not uncommon for researchers to talk of p=.1 as “marginally significant”, yet if the sample size is 9 or greater then the JZS Bayes factor implies that the data favour the null. (For p=.01 and p=.001 the cross-over sample sizes are 480 and 32073, respectively.) Although Bayesian inference has the advantage of allowing evidence for the null, it may be disheartening for JDM researchers to think that a Bayes factor approach will make it harder to assert the alternative hypothesis when this is most often what they wish to do.
Figure 1: JZS Bayes factor as a function of sample size for various p-values. 
The Neyman-Pearson (N-P) approach is distinct from Fisher’s in that (1) the researcher specifies an alternative to the null, and (2) rather than reporting a p-value, the researcher reports α and β, the probabilities of type I and type II errors (the long-run frequencies with which the null will be erroneously rejected/accepted) (e.g., Neyman, 1950; see also Hubbard & Bayarri, 2003, and Lehmann, 1993). Typically, in advance of data collection the researcher specifies the alternative hypothesis as a particular effect size δ >0 and performs a power calculation to determine the sample size needed to achieve a particular type II error rate 2. Many JDM researchers employ this approach (e.g., Hilbig, 2008; Matthews, 2011), but its use is not systematic. For example, APA guidelines stipulate reporting exact p-values even though these are irrelevant to N-P inference (American Psychological Association, 2009, p.34).
When considering the competing, Bayesian approach, we can note the following:
1. The specification of an alternative to the null is common to N-P and Bayesian hypothesis testing, but the N-P approach is concerned with inductive behaviour, not inference. From this perspective, it is meaningless to talk about the probability of a particular hypothesis being true—it either is or is not. We can only seek to specify the long run frequency with which we draw an incorrect conclusion: “Thus, to accept a hypothesis H means only to decide to take action A rather than action B. This does not mean we necessarily believe that the hypothesis H is true” (Neyman, 1950, p. 259). In Bayesian hypothesis testing, by contrast, probabilities represent degrees of belief (or the “normative convictions a person should have given the constraints and information made explicit in the statement of the problem”, Dienes, 2011, p. 7).
2. Correspondingly, the N-P approach does not quantify evidence. An experiment for which the t-statistic is fractionally above the critical value for rejection of the null with α= .05 is interpreted no differently from an identical experiment in which the t-statistic is five times larger (see e.g., Berger, 2003, for discussion).
3. The N-P approach typically involves specifying a single alternative (such as an effect size of 0.5) whereas the Bayesian approach allows specification of a range of effect sizes with differing prior probabilities. The price of this flexibility is that inference depends on the choice of a prior distribution, which may seem arbitrary and subjective (see below).
4. Like Fisher’s approach, N-P testing violates the likelihood principle: inference depends not only on the observed data but also on the sampling plan, whether the tests are planned or post hoc, and the number of tests to be conducted. For example, researchers seek to minimize type I error rates by adjusting the alpha level for multiple tests, but this raises the problem of specifying in advance how many tests will (or might) be conducted. The Bayes factor quantifies the evidence for one hypothesis versus another and multiple hypotheses may be compared without difficulty and post hoc (e.g., Gallistel, 2009).
5. There has been a growing emphasis on reporting effects sizes and their associated confidence intervals (CIs, see, e.g., Cumming & Finch, 2005). It is certainly worth reporting this information, but because confidence intervals are based on the same frequentist logic as Neyman-Pearson hypothesis testing, the same comments apply: the CIs depend on the sampling plan and researcher intentions, they do not quantify evidence, and an effect size whose 95% confidence interval does not span zero may nonetheless provide stronger support for the null than for an alternative with a reasonable prior. As Di Stefano, Fidler, and Cumming (2005) note: “It is somewhat frustrating that confidence intervals do not provide us with the probability that the interval contains the true effect, a value that would be particularly useful—to achieve this we would have to create intervals using a Bayesian approach.” We discuss this approach below.
The power calculations used in N-P testing raise the issue of effect size, and it is instructive to examine the influence of effect size on the Bayes factor. Figure 2 shows the expected Bayes factors and posterior probabilities as a function of sample size for three different effects. When there is a large effect, the Bayes factor strongly favours the alternative even with relatively small samples. However, when the true effect is smaller, increasing the data initially strengthens the evidence for the null, and only when very large data sets have been collected does the Bayes factor shift in favour of the alternative hypothesis. Rouder et al. (2009) describe this behaviour as “ideal” (p. 233), because very small effects imply approximate invariance. The null is unlikely to be exactly true, so the behaviour of the Bayes factor allows researchers to gain positive evidence for the null (or an approximate invariance) at realistic sample sizes, safe in the knowledge that the small deviation from the null would become apparent eventually. Despite this, some researchers may be troubled by the inverted U-shaped curve for small effects.
Figure 2: Change in expected Bayes factor (left panel) and posterior probability of the null Pr(H0|D) (right panel) when the sample size is increased for each of three true effect sizes: a large effect (δ=2.0), a small effect (δ=0.2) and a very small effect (δ=0.02). The plotted values were obtained by Monte Carlo simulation in which repeated samples of the given size were drawn from a normal distribution with mean equal to δ and unit standard deviation. The data represent the results using the unit information prior (see Appendix) because Rouder et al. (2009) explain that the integration required in the calculation of the JZS Bayes factor becomes unstable at very large N; nonetheless, running the analysis with the JZS prior produces the same pattern of results. Each point is based on 10000 random samples. 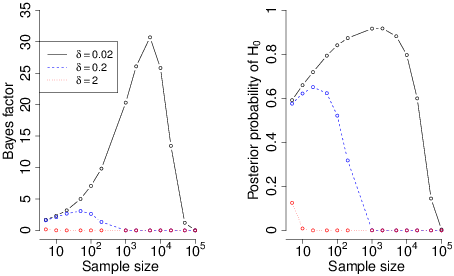
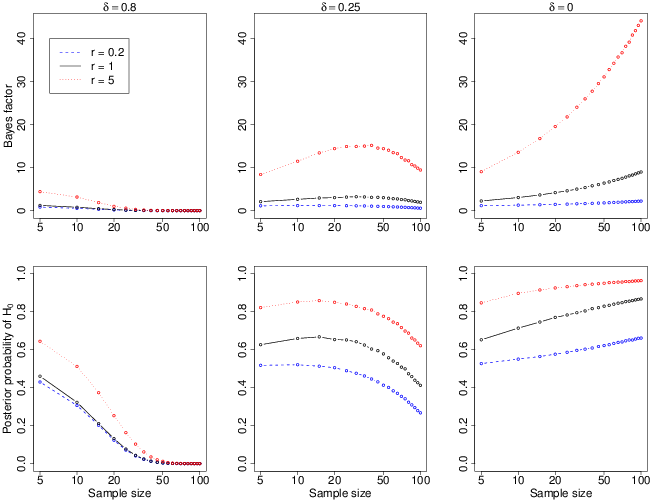
Figure 3: The effects of changing the prior. The upper panels show changes in the Bayes factor as sample size increases; the lower panels show the change in the posterior probability of the null (assuming equal prior probabilities for H0 and H1). The plots show the dependency of the Bayes factor on the choice of prior for each of three true effect sizes. Each data point represents the average from 10000 random samples. The leftmost plot shows the results when the true state of nature comprises a substantial effect, δ=0.8. In this case, the most widely-dispersed prior (r=5) favours the null more than the cases where the prior assumes a smaller effect, but as the sample size rises this difference is rapidly overwhelmed by the data. The middle panel shows the results for a smaller effect size, δ=0.25. Here the three priors differ substantially in their support for the null and in the sample size that is required before the Bayes factor favours the alternative hypothesis. For example, with a sample of 100 the choice of r=0.2 indicates a posterior probability for the null that approaches 0.25, indicating “positive evidence” for the alternative hypothesis, but when r=5, Pr(H0) is about .60, providing “weak evidence” for the null. The situation is most pronounced in the right-hand panel, where δ=0 (the null hypothesis is true.) Here the choice of a large r means that the data quickly favour the null; however, choice of a small r—corresponding to the belief that the data will not differ much from the null hypothesis—provides little clear evidence one way or the other even when N=100.
The foregoing relates Bayesian hypothesis testing to alternative modes of inference. Although we have emphasized its advantages, the Bayesian approach is far from universally approved (see e.g., Hacking, 1965; 2001, for discussion). The most widespread objection is that Bayesian hypothesis testing requires the specification of prior probabilities.
Prior probabilities enter Bayesian hypothesis testing at two points: we specify prior probability density functions for the parameters of the models we are testing, and prior odds for the competing hypotheses. The former are intrinsic to the formulation of statistical hypotheses and, as such, determine the balance of evidence provided by the data; the latter reflect our prior beliefs/knowledge, and have no effect on the balance of evidence from the data—rather, they shape how this evidence is used to arrive at a new belief state.
Critics of Bayesian hypothesis testing (including Fisher and Neyman) attack the need to specify prior distributions for model parameters as introducing inappropriate subjectivity into statistical inference. For a Bayesian, however, specifying prior distributions for the parameters is part of establishing the hypotheses that we wish to test, and the choice of prior reflects relevant knowledge. Different priors give rise to different Bayes factors, but this is just as one would expect (and require) when testing different models. From this perspective, the dependence of inference on the specification of a prior parameter distribution is a strength, not a weakness. Deciding between these positions is not a goal of this article (for discussions, see Berger, 2003; Hacking, 1965, 2001; Jaynes, 2003; Neyman, 1950; Sterne & Davey Smith, 2001; Trafimow, 2003, 2005; Vanpaemel, 2010; Wagenmakers, 2007). Instead, we will aim to get a sense of how the choice of prior influences Bayesian hypothesis testing.
The choice of prior may be based on an experimenter’s existing knowledge, or on an “objective” principle. “Objective” priors are typically chosen to be uninformative, with the probability density spread thinly over the range for which they are defined. The JZS prior employed above is an example of an uninformative prior. It captures the intuition that increasingly large effects sizes are increasingly unlikely, and it is intended to carry very little information (Kass & Raftery, 1995; see Appendix). However, researchers can also incorporate their knowledge about the outcomes which are likely to arise in a particular experimental context (e.g., Gallistel, 2009, Vanpaemel, 2010). For the JZS t-test, we can scale the JZS prior on effect size, such that δ r × Cauchy, where r is a scale factor (Rouder et al., 2009). Increasing r increases the dispersion of the prior distribution, making extreme effects more plausible.
Figure 3 shows how r influences the Bayes factor for three true effect sizes. It illustrates a core point: the choice of prior can have a marked influence on Bayesian inference when the sample sizes are around those typical of many JDM experiments. For some, this will be reason enough to stick with NHST. For others, the role of the prior reflects an essential truth about the scientific enterprise—that if we are to use data to choose between competing beliefs, the choice will depend upon exactly how those beliefs are constituted (e.g., Jaynes, 2003; Vanpaemel, 2010).
We saw above that the Bayes factor sometimes suggests a different conclusion from the p-value. Such discrepancies inevitably depend on the choice of prior for the alternative hypothesis. For example, in the Critcher and Gilovich (2008, Study 1) example, it might be objected that the results are a consequence of the diffuse JZS prior: if the prior concentrated greater weight on smaller effect sizes, the results would, like NHST, favour the alternative. One general strategy advocated by Gallistel (2009) is to undertake a sensitivity analysis based on “varying the vagueness”. Gallistel focuses on the case where the null specifies a value for a parameter and the alternative specifies a uniform distribution of increments to the null value; extending the range of this distribution increases the vagueness of the alternative. Gallistel plots the Bayes factor as a function of the limit(s) on the increment prior, and suggests that “the null is rejected only when this function has a minimum substantially below the odds reversal line” (that is, when the minimum Bayes factor is much less than 1) (Gallistel, 2009, p. 452). In some cases, one hypothesis or the other is “unbeatable”: the Bayes factor is above (or below) the reversal line across the whole range of maximum assumed effect sizes.
Figure 4: The effects of changing the prior on the Bayes factor for the data from Jacowitz and Kahneman (1995) and Critcher and Gilovich (2008, Study 1). Points above the dotted reversal line favour the null; below the line they favour the alternative. Small values of r favour the alternative hypothesis; as the prior distribution of effect sizes is made more diffuse (that is, as larger effects are given greater weight) the balance shifts to favour the null. As r approaches zero, the alternative becomes indistinguishable from the null and the Bayes factor approaches 1. For the Jacowitz and Kahneman data, the Bayes factor favours the alternative for r up to 56.1 (corresponding to a very diffuse prior); for the Critcher and Gilovich experiment, the Bayes factor favours the null once r>0.70. 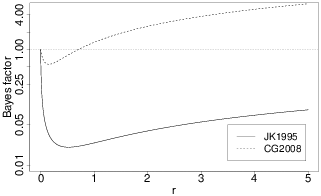
Figure 4 illustrates this approach by plotting the JZS Bayes factor as a function of the scale factor r for the studies by Jacowitz and Kahneman (1995) and Critcher and Gilovich (2008, Study 1) discussed above (see the online appendix to Wagenmakers, Wetzels, Borsboom, & van der Maas, 2011, for another illustration). For the Jacowitz and Kahneman experiment, the minimum Bayes factor favours the alternative by about 50:1 (when r=0.52) and the Bayes factor is below the reversal line for a wide range of r values. For the Critcher and Gilovich data, the Bayes factor minimum is 0.56 (favouring the alternative by about 1.8 to 1) when r=0.15, providing only weak support for the alternative; for a reasonable range of scale factors the data are not particularly compelling either way. Note that as r approaches zero the null and alternative become indistinguishable and the Bayes factor tends to 1, and that as r grows larger and the alternative hypothesis becomes ever more vague, so the data increasingly favour the null (although in some situations analytic constraints limit the maximum vagueness of the prior—see, e.g., Gallistel, 2009).
Some researchers suggest that Bayes factors routinely be accompanied by this kind of sensitivity analysis, indicating the effects of choosing different priors (Liu & Aitkin, 2008). More general information regarding robust Bayesian analysis can be found in Berger (1990, 1993; see also Gelman, 2006).
When specifying priors, it is important that the researcher be clear about which hypotheses they wish to compare. Consider a study in which 100 students take a statistics test before and after a course on Bayesian inference. The average improvement is 2% (SD=10%), and the paired-samples t(99) = 2.00. The corresponding p-value is .048 suggesting rejection of the null, but the JZS BF is 1.85, weakly favouring the null hypothesis. What should one expect in a replication of this study? A reviewer commented that it seems reasonable to think that a positive effect will be more likely than a negative one, whereas the Bayes factor favours the null, suggesting that both directions are equally likely.
A key point here is that the results of the Bayesian analysis depend upon the hypotheses we compare. The JZS Bayes factor contrasts the hypothesis of an effect size of precisely zero (the null) with the hypothesis of an effect whose probable size is Cauchy distributed about zero. If we set out to test an ordinal constraint (such as whether the data are more likely to have come from a distribution with an effect size which is positive or negative) then we would calculate a different Bayes factor. Morey and Rouder (2011) discuss the calculation of Bayes factors for this kind of ordinal constraint, and suggest contrasting Hn, under which the effect size is a half Cauchy on the negative reals (i.e., the effect is negative and small effects are more likely than large ones), with Hp, in which the prior distribution for effect size is a half Cauchy on the positive reals (the effect is positive and small effects are more likely than large ones). For the example above, the resulting Bayes factor favours the hypothesis of a positive effect by a factor of about 38.5.3 Thus, given a choice between no effect and an effect of unspecified direction with small absolute values more likely than large ones, the data favour the hypothesis of zero effect; but given a choice between a positive effect and a negative effect (with small absolute values again more likely than large ones), the data strongly favour a positive effect. There is nothing inconsistent about these inferences: different questions produce different answers. Morey and Rouder provide an extensive discussion of the Bayes factor approach to testing directional hypotheses and hybrid models in which the null is defined as a range of small effects rather than precisely zero effect.
This example also raises the more general question of how researchers can use the results of a Bayesian analysis to generate predictions for future data. Briefly, one can use the data from the first experiment to update the effect size prior and use the resulting posterior distribution as a data-generating model to obtain predictions for a replication experiment. This process can be repeated for competing hypotheses, with the predictions of each model weighted by that model’s posterior probability. For examples and discussion, see Kruschke (2010) and Iverson, Wagenmakers, and Lee (2010).
The Bayes factor quantifies the evidence provided by the data, irrespective of the researcher’s prior beliefs—which some have argued makes it ideal for scientific communication (e.g., Jeffreys, 1961; Rouder & Morey, 2011). However, the conversion from Bayes factor to posterior odds depends on the prior odds, Pr(H0)/Pr(H1). In the examples above we treated the two hypotheses as equally likely a priori, but this need not be the case. For example, in a Bayesian analysis of Bem’s (2011) recent data on precognition, Rouder and Morey (2011) find a Bayes factor of about 40 in favour of the hypothesis that people can predict the future presentation of valenced non-erotic stimuli. This Bayes factor quantifies the evidence in the data and specifies how beliefs should be updated, but the results of this updating will depend on the beliefs held before the experiment. Rouder and Morey suggest that most researchers would strongly favour the null hypothesis—because precognition contravenes established biological and physical principles. If one quantified this belief with prior odds of Pr(H0)/Pr(H1)=106, the posterior odds following Bem’s experiment are (106/1)*(1/40) = 25000:1 in favour of the null. Note that the prior odds of a million to one are purely illustrative: different researchers will have different prior odds based on their varying knowledge of relevant research—but the Bayes factor nonetheless quantifies how those beliefs should be revised in light of the new data.
One might also specify prior odds on the basis of a general belief about the probable truth of the null hypothesis. A reviewer commented that we typically give the null hypothesis “all the chances we can”, which suggests a prior belief in the truth of the null. Similarly, Sterne and Davey Smith (2001) assume that, in epidemiological research, only 10% of the null hypotheses tested are false. Setting prior odds of 9:1 in favour of the null means that it takes stronger evidence (quantified by the Bayes factor) to shift our posterior beliefs in favour of the alternative.
Many researchers will be uncomfortable with the subjectivity which prior odds seem to represent, and with the idea that different people may draw different conclusions from the same data. (Indeed, NHST arose from a desire to make inductive inference “objective”—see e.g., Hubbard & Bayarri, 2003). A Bayesian will counter that prior odds capture relevant knowledge, and that if researchers have differing prior knowledge then it is only reasonable that they reach different conclusions following a given experiment. One position stresses the Bayes factor as a quantification of the evidence provided by the data which does not in itself lead to a choice between competing hypotheses: people may hold differing prior beliefs (based on differing knowledge) and use the Bayes factor to update these beliefs. One practical approach is to assume that both hypotheses are equally likely, run our first experiment, calculate the posterior odds using the Bayes factor, and then use these as the prior odds for the next experiment. Thus, research following on from the experiment by Jacowitz and Kahneman (1995) discussed above might begin with prior odds that are 42:1 in favour of the hypothesis that provision on an anchor affects confidence. The existing data give us reason to believe in this hypothesis, increasing the weight of contradictory evidence which will be required to shift our belief back towards the null.
We have focussed on the Bayes factor as a quantification of the evidence for competing hypotheses. However, in many situations we are more interested the magnitude of an effect (or, more generally, the value of a model parameter) than in choosing between null and alternative hypotheses. Adopting a Bayesian approach, researchers can specify a prior distribution for the parameter and update this in the light of the data to obtain a posterior distribution which specifies the probability that the parameter takes any particular value. This information can be summarized by reporting, for example, the mean and a “credible interval” containing 95 percent of the posterior density. Unlike frequentist confidence intervals, the credible intervals of Bayesian analysis do not depend on the researcher’s intentions or sampling plan—we can, for example, keep collecting and inspecting data indefinitely—and have the advantage that the prior distribution encapsulates existing knowledge about the parameter in question. Moreover, for studies examining multiple effects the posterior will be a joint probability distribution indicating the credibility of all combinations of parameter values, and this posterior distribution can be used for multiple comparisons without having to worry about corrections for multiple tests (see Kruschke, 2010, for a worked example).
This parameter-estimation approach readily extends to hierarchical models in which, for example, we assume that the effect size for each participant is drawn from an overarching distribution with its own hyperparameters, where we specify prior distributions for these hyperparameters rather than for the effect size itself. In this way, information gained from one participant shapes the predictions made about the others. An introduction to the hierarchical approach and discussion of its advantages can be found in Lee and Vanpaemel (2008), Rouder and Lu (2005), and Shiffrin, Lee, Kim, and Wagenmakers (2008). For recent applications to JDM research see van Ravenzwaaij et al., (2011) and Nilsson, Rieskamp, and Wagenmakers (2011).
The JZS t-test used here is accessible but limited. Wetzels, Raaijmakers, Jakab, and Wagenmakers (2009) have introduced a more flexible Bayesian t-test, the Savage-Dickey t-test, which can cope with order restrictions (directional hypotheses) and unequal variances, but which requires Markov Chain Monte Carlo techniques. The authors provide an R code instantiation which makes use of the freely-available WinBUGS program (Lunn, Thomas, Best, & Spiegelhalter, 2000). An application of this test to work in judgment and decision making can be found in Otto (2010). Morey and Rouder (2011) also describe Bayes factors for ordinal constraints and for interval null hypotheses (i.e., for testing approximate equality), while Rouder and Morey (2010) describe the use of Bayes factors in regression.
For more complex experiments, researchers might consider the Bayesian Information Criterion (BIC; Schwarz, 1978). The BIC for a given model depends on its maximum likelihood, the number of its free parameters, and the size of the data set (although it is insensitive to functional form, unlike the approach described above). The BIC can be transformed to approximate Pr(D|H), meaning that the difference between two BIC values can be used to approximate the Bayes factor (Wagenmakers, 2007, Appendix B). One can use the sum of squared errors reported in the ANOVA output of standard statistical packages to calculate the BIC and Bayes factor, permitting Bayesian hypothesis testing using familiar statistical output (Glover & Dixon, 2004; Wagenmakers, 2007) .
We have focussed on the JZS t-test because it provides a Bayesian counterpart to a very familiar test. The results are sensitive to the choice of the scale parameter r (Figure 3), yet in many situations the researcher will feel that they have no idea what value r should take, or whether the Cauchy distribution on effect size implemented in the JZS prior is appropriate at all. The author urges two points. Firstly, as researchers become more comfortable with the principles and techniques of Bayesian inference, they will become more adroit at tailoring the prior to the inference problem at hand—for example, by constructing informative priors using hierarchical methods (e.g., Vanpaemel, 2011). The shortcomings of the JZS t-test as a generic tool should not obscure the merits of a shift towards Bayesian inference in general. Secondly, when it is theoretically meaningful to compare the null against a particular alternative, the Bayes factor provides a principled measure of evidence which can be used to update existing beliefs. However, sometimes we are more interested in estimating the size of an effect (and in quantifying our uncertainty) than we are in choosing between the null and a more-or-less arbitrary alternative. In these cases, effect size estimation using (hierarchical) Bayesian techniques provide a powerful tool.
What might judgment and decision making research look like if we took a Bayesian approach to hypothesis testing? First, Bayesian inference would affect the mechanics of how we conduct our studies, influencing sample sizes and legitimating the use of ad hoc sampling plans. Second, our results would be couched in terms of the balance of evidence for competing hypotheses rather than categorical accept/reject decisions. Third, researchers would sometimes argue that their data provide positive evidence for the null, and it will typically be harder to assert the truth of the alternative hypothesis. More generally, the substantive conclusions that we draw from our experiments would sometimes be different under a Bayesian regimen. Finally, we can expect disagreements about the choice of prior. Although some priors are labelled “objective”, there is more than one such prior and the choice may influence inference. More optimistically, debate about the choice of prior may encourage clear thinking regarding the nature both of our hypotheses and of the inference problem itself.
Acker, F. (2008). New findings on unconscious versus conscious thought in decision making: Additional empirical data and meta-analysis. Judgment and Decision Making, 3, 292–303.
American Psychological Association. (2001). The publication manual of the American Psychological Association.(6th ed.) Washington, DC. American Psychological Association.
Ariely, D., Loewenstein, G., & Prelec, D. (2003). “Coherent arbitrariness”: Stable demand curves without stable preferences. Quarterly Journal of Economics, 118, 73–105
Bakan, D. (1966). The test of significance in psychological research. Psychological Bulletin, 66, 423–437.
Bem, D. (2011). Feeling the future: Experimental evidence for anomalous retroactive influences on cognition and affect. Journal of Personality and Social Psychology, 100, 407–425.
Berger, J. O. (1990). Robust Bayesian analysis: Sensitivity to the prior. Journal of Statistical Planning and Inference, 25, 303–328.
Berger, J. (1993). An overview of robust Bayesian analysis. (Technical Report #93–53C). Retrieved from Purdue University, Department of Statistics website: http://www.stat.purdue.edu/research/technical_reports/ pdfs/1993/tr93–53c.pdf
Berger, J. O. (2003). Could Fisher, Jeffreys and Neyman have agreed on testing? Statistical Science, 18, 1–32.
Block, R. A., & Harper, D. R. (1991). Overconfidence in estimation: Testing the anchoring-and-adjustment hypothesis. Organizational Behavior and Human Decision Processes, 49, 188–207.
Botella, J., Ximénez, C., Revuelta, J., & Suero, M. (2006). Optimization of sample size in controlled experiments: The CLAST rule. Behavior Research Methods, 38, 65–76.
Butler, S. A. (1986). Anchoring in the judgmental evaluation of audit samples. The Accounting Review, 61, 101–111.
Calvillo, D. P., & Penaloza, A. (2009). Are complex decisions better left to the unconscious? Further failed replications of the deliberation-without-attention effect. Judgment and Decision Making, 4, 509–517.
Carlson, B. W. (1990). Anchoring and adjustment under risk. Journal of Experimental Psychology: Learning, Memory, and Cognition, 16, 665–676.
Cervone, D., & Peake, P. K. (1986). Anchoring, efficacy, and action: The influence of judgmental heuristics on self-efficacy judgments and behavior. Journal of Personality and Social Psychology, 50, 492–501.
Chapman, G. B., & Bornstein, B. H. (1996). The more you ask for, the more you get: Anchoring in personal injury verdicts. Applied Cognitive Psychology, 10, 519–540.
Chapman, G. B., & Johnson, E. J. (1999). Anchoring, activation, and the construction of values. Organizational Behavior and Human Decision Processes, 79, 115–153.
Critcher, C. R., & Gilovich, T. (2008). Incidental environmental anchors. Journal of Behavioural Decision Making, 21, 241–251.
Cumming, G., & Finch, S. (2005). Inference by eye: Confidence intervals and how to read pictures of data. American Psychologist, 60, 170–180.
DeGroot, M. H., & Schervish, M. J. (2002). Probability and statistics. 3rd Ed. London: Addison Wesley.
Dienes, Z. (2011). Bayesian versus orthodox statistics: Which side are you on? Perspectives on Psychological Science, 6, 274–290.
Di Stefano, J., Fidler, F., & Cumming, G. (2005). Effect size estimates and confidence intervals: An alternative focus for the presentation and interpretation of ecological data. In A.R. Burk (Ed.) New trends in ecology research (pp. 71–102). New York: Nova Science Publishers.
Edwards, W., Lindman, H., & Savage, L. J. (1963). Bayesian statistical inference for psychological research. Psychological Review, 70, 193–242.
Englich, B., & Mussweiler, T.(2001). Sentencing under uncertainty: Anchoring effects in the courtroom. Journal of Applied Social Psychology, 31, 1535–1551.
Epley, N., & Gilovich, T. (2001). Putting the adjustment back in the anchoring and adjustment heuristic: Differential processing of self-generated and experimenter-provided anchors. Psychological Science, 12, 391–396.
Epley, N., & Gilovich, T. (2005). When effortful thinking influences judgmental anchoring: Differential effects of forewarning and incentives on self-generated and externally provided anchors. Journal of Behavioural Decision Making, 18, 199–212.
Faul, F., Erdfelder, E., Lang, A-G., & Buchner, A. (2007). G*Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behavior Research Methods, 39, 175–191.
Fisher, R. A. (1960). The design of experiments. (7th ed.) London: Oliver and Boyd.
Fisher, R. A. (1970).Statistical methods for research workers. (14th ed.) Edinburgh: Oliver and Boyd.
Frick, R. W. (1998). A better stopping rule for conventional statistical tests. Behavior Research Methods, Instruments, & Computers, 30, 690–697.
Gallistel, C. R. (2009). The importance of proving the null. Psychological Review. 116, 439–453.
Gelman, A. (2006). The boxer, the wrestler, and the coin flip: A paradox of robust Bayesian inference and belief functions. The American Statistician, 60, 146–150.
Glover, S., & Dixon, P. (2004). Likelihood ratios: A simple and flexible statistic for empirical psychologists. Psychonomic Bulletin & Review, 11, 791–806.
Hacking, I. (1965). Logic of statistical inference. London: Cambridge University Press.
Hacking, I. (2001). An introduction to probability and inductive logic. Cambridge: Cambridge University Press.
Hilbig, B. E. (2008). Individual differences in fast-and-frugal decision making: Neuroticism and the recognition heuristic. Journal of Research in Personality, 42, 1641–1645.
Hubbard, R., & Bayarri, M. J. (2003). Confusion over measures of evidence (p’s) versus errors (α’s) in classical statistical testing. The American Statistician, 57, 171–178.
Iverson, G. J., Lee, M. D., & Wagenmakers, E-J. (2009). prep misestimates the probability of replication. Psychonomic Bulletin & Review, 16, 424–429.
Iverson, G. J., Wagenmakers, E-J., & Lee, M. D. (2010). A model-averaging approach to replication: The case of prep. Psychological Methods, 15, 172–181.
Jacowitz, K. E., & Kahneman, D. (1995). Measures of anchoring in estimation tasks. Personality and Social Psychology Bulletin, 21, 1161–1166.
Jaynes, E. T. (2003). Probability theory: The logic of science. Cambridge: Cambridge University Press.
Jeffreys, H. (1961). Theory of probability. 3rd ed. Oxford: Clarendon Press.
Kass, R. E., & Raftery, A. E. (1995). Bayes factors. Journal of the American Statistical Association, 90, 773–795.
Kass, R. E., & Wasserman, L. (1995). A reference Bayesian test for nested hypotheses and its relationship to the Schwarz criterion. Journal of the American Statistical Association, 90, 928–934.
Killeen, P. R. (2005). An alternative to null-hypothesis significance tests. Psychological Science, 16, 345–353.
Kruschke, J. K. (2010). Bayesian data analysis. Wiley Interdisciplinary Reviews: Cognitive Science, 1, 658–676.
LeBoeuf, R. A., & Shafir, E. (2006). The long and short of it: Physical anchoring effects. Journal of Behavioral Decision Making, 19, 393–406.
Lee, P. M. (1997). Bayesian Statistics: An Introduction. 2nd Ed. New York: Wiley.
Lee, M. D., & Vanpaemel, W. (2008). Exemplars, prototypes, similarities, and rules in category representation: An example of hierarchical Bayesian analysis. Cognitive Science, 32, 1403–1424.
Lee, M. D., & Wagenmakers, E-J. (2005). Bayesian statistical inference in psychology: Comment on Trafimow (2003). Psychological Review, 112, 662–668.
Lehmann, E. L. (1993). The Fisher, Neyman-Pearson theories of testing hypotheses: One theory or two? Journal of the American Statistical Association, 88, 1242–1249.
Liu, C. C., & Aitkin, M. (2008). Bayes factors: Prior sensitivity and model generalizability. Journal of Mathematical Psychology, 52, 362–375.
Lunn, D. J., Thomas, A., Best, N., & Spiegelhalter, D. (2000). WinBUGS—a Bayesian modelling framework: Concepts, structure, and extensibility. Statistics & Computing, 10, 325–337.
Matthews, W. J. (2011). Can we use magnitude estimation to dissect the internal clock? Differentiating the effects of pacemaker rate, switch latencies, and judgment processes. Behavioural Processes, 86, 68–74.
Matthews, W. J., & Stewart, N. (2009). Psychophysics and the judgment of price: Judging complex objects on a non-physical dimension elicits sequential effects like those in perceptual tasks. Judgment and Decision Making, 4, 64–81.
Miller, J. (2009). What is the probability of replicating a statistically significant effect? Psychonomic Bulletin & Review, 16, 617–640.
Morey, R. D., & Rouder, J. N. (2011). Bayes factor approaches for testing interval null hypotheses. Psychological Methods, 16, 406–419.
Mussweiler, T., & Strack, F. (1999). Hypothesis-consistent testing and semantic priming in the anchoring paradigm: A selective accessibility model. Journal of Experimental Social Psychology, 35, 136–164.
Neyman, J. (1950). First course in probability and statistics. New York: Holt, Rinehart and Winston.
Nickerson, R. S. (2000). Null hypothesis significance testing: A review of an old and continuing controversy. Psychological Methods, 5, 241–301.
Nilsson, H., Rieskamp, J., & Wagenmakers, E-J. (2011). Hierarchical Bayesian parameter estimation for cumulative prospect theory. Journal of Mathematical Psychology, 55, 84–93.
Northcraft, G. B., & Neale, M. A. (1987). Experts, amateurs, and real estate: An anchoring-and-adjustment perspective on property pricing decisions. Organizational Behavior and Human Decision Processes, 39, 84–97.
Otto, A. R. (2010). Three attempts to replicate the behavioral sunk-cost effect: A note on Cunha and Caldieraro (2009). Cognitive Science, 34, 1379–1383.
Raftery, A. E. (1995). Bayesian model selection in social research. Sociological Methodology, 25, 111–163.
Rosenthal, R., & Gaito, J. (1963). The interpretation of levels of significance by psychological researchers. Journal of Psychology, 55, 33–38.
Rouder, J. N., & Lu, J. (2005). An introduction to Bayesian hierarchical models with an application in the theory of signal detection. Psychonomic Bulletin & Review, 12, 573–604.
Rouder, J. N., & Morey, R. D. (2010). Bayesian testing in regression. Manuscript submitted for publication.
Rouder, J. N., & Morey, R. D. (2011). A Bayes-factor meta analysis of Bem’s ESP claim. Psychonomic Bulletin & Review, 18, 682–689.
Rouder, J. N., Speckman, P. L., Sun, D., Morey, R. D., & Iverson, G. (2009). Bayesian t tests for accepting and rejecting the null hypothesis. Psychonomic Bulletin & Review, 16, 225–237.
Schwarz, G. (1978). Estimating the dimension of a model. Annals of Statistics, 6, 461–464.
Shiffrin, R. M., Lee, M. D., Kim, W., & Wagenmakers, E-J. (2008). A survey of model evaluation approaches with a tutorial on hierarchical Bayesian methods. Cognitive Science, 32, 1248–1284.
Sterne, J. A. C., & Davey Smith, G. (2001). Sifting the evidence—what’s wrong with significance tests? British Medical Journal, 322, 226–231.
Thorsteinson, T. J., Breier, J., Attwell, A., Hamilton, C., & Provette, M. (2008). Anchoring effects on performance judgments. Organizational Behavior and Human Decision Processes, 107, 29–40.
Thorsteinson, T. J., & Withrow, S. (2009). Does unconscious thought outperform conscious though on complex decisions? A further examination. Judgment and Decision Making, 4, 235–247
Trafimow, D. (2003). Hypothesis testing and theory evaluation at the boundaries: Surprising insights form Bayes’s theorem. Psychological Review, 110, 526–535.
Trafimow, D. (2005). The ubiquitous Laplacian assumption: Reply to Lee and Wagenmakers (2005). Psychological Review, 112, 669–674.
Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and Biases. Science, 185, 1124–1131.
van Ravenzwaaij, D., Dutilh, G., & Wagenmakers, E-J. (2011). Cognitive model decomposition of the BART: Assessment and application. Journal of Mathematical Psychology, 55, 94–105.
Vanpaemel, W. (2010). Prior sensitivity in theory testing: An apologia for the Bayes factor. Journal of Mathematical Psychology, 54, 491–498.
Vanpaemel, W. (2011). Constructing informative model priors using hierarchical methods. Journal of Mathematical Psychology, 55, 106–117.
Wagenmakers, E-J. (2007). A practical solution to the pervasive problems of p values. Psychonomic Bulletin & Review, 14, 779–804.
Wagenmakers, E-J., Lodewyckx, T., Kuriyal, H., & Grasman, R. (2010). Bayesian hypothesis testing for psychologists: A tutorial on the Savage-Dickey method. Cognitive Psychology, 60, 158–189.
Wagenmakers, E-J., Wetzels, R., Borsboom, D., & van der Maas, H. L. J. (2011). Why psychologists must change the way they analyze their data: The case of Psi: Comment on Bem (2011). Journal of Personality and Social Psychology, 100, 426–432.
Wansink, B., Kent, R. J., & Hoch, S. J. (1998). An anchoring and adjustment model of purchase quantity decisions. Journal of Marketing Research, 35, 71–81.
Wetzels, R., Raaijmakers, J. G. W., Jakab, E., & Wagenmakers, E-J. (2009). How to quantify support for and against the null hypothesis: A flexible WinBUGS implementation of a default Bayesian t test. Psychonomic Bulletin & Review, 16, 752–760.
Wilkinson, L. & The Task Force on Statistical Inference. (1999). Statistical methods in psychology journals: Guidelines and explanations. American Psychologist, 54, 594–604.
Under the null hypothesis the population is normally distributed with mean µ=0 and variance σ2. Rather than specifying a single mean for the alternative hypothesis, we assume a distribution of values which is parameterized in terms of the effect size δ=µ/σ. (The null has δ=0.) Specifically, the prior distribution of effect size under the alternative hypothesis is assumed to be normal: δ Normal(0,σδ2).
Larger values of σδ2 put greater relative weight on larger effect sizes, and if σδ2 is very large then the resulting Bayes factor will strongly favour the null. One option is to set σδ2=1, which is the unit-information prior; it assumes that small effects occur more often than large ones, and avoids putting much weight on unreasonably large effect sizes. It is also relatively uninformative, carrying only the amount of information in a single observation (Kass & Wasserman, 1995).
The JZS t-test assumes an even less informative prior by specifying a distribution of values for σδ2. Zellner and Siow (1980, cited in Rouder et al., 2009) suggest that σδ2 take an inverse χ2 distribution on 1 degree of freedom. Under this distribution the density of σδ2 is concentrated near 1.0 and falls off rapidly at very small and very large values. Placing a normal on effect size that has a variance given by an inverse chi-square is equivalent to having the effect size follow a Cauchy distribution—a t-distribution with one degree of freedom (see, e.g., DeGroot & Schervish, 2002, p.406). The Cauchy gives more weight to large effects than does the standard normal, resulting in a slight shift in favour of the null when one calculates the Bayes factor.
The choice of prior for the population variance σ2 is less important because it enters both hypotheses, so the effects will cancel when the Bayes factor is calculated. Rouder et al. (2009) use the Jeffreys prior on variance, p(σ2)=1/σ2 (Jeffreys, 1961) and refer to the combination of the Cauchy prior on effect size and the Jeffreys prior on variance as the JZS prior.
Having chosen prior distributions for the parameters of the two hypotheses, one can calculate their marginal likelihoods Pr(D|H0) and Pr(D|H1) by integrating over the parameter space as described in the main text. Rouder et al. (2009) present the resulting Bayes factor as:
| B01= |
|
| (1+ |
| )−(v+1)/2 · |
| (2π)−1/2g−3/2e−1/(2g)dg | ⎤ ⎥ ⎦ |
(1) where N is the sample size, t is the usual one-sample t-statistic, and v is the degrees of freedom, N−1.
Equation 1 can be adapted to cover the case where the researcher wishes to test whether two independent samples are drawn from populations with different means. This requires three substitutions: the t-value is that for two independent samples; the effective sample size is NxNy/(Nx+Ny); and the degrees of freedom v=Nx+Ny−2 (Rouder et al., 2009).
This document was translated from LATEX by HEVEA.