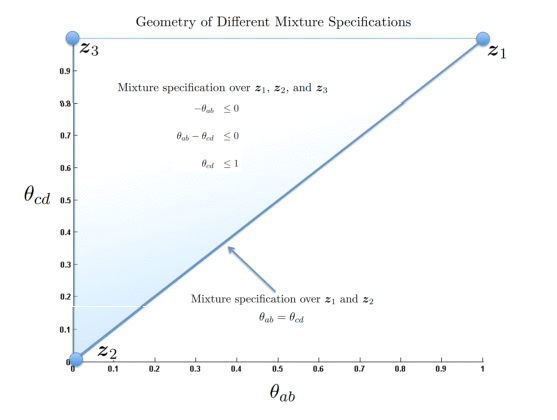
| Figure 1: This figure plots the constraints placed on the parameter space Θ for the three-strategy mixture specification over z1, z2, and z3; as well as the two-strategy mixture specification over z1 and z2. |
Judgment and Decision Making, vol. 6, no. 8, December 2011, pp. 800-813
A shift in strategy or “error”? Strategy classification over multiple stochastic specificationsClintin P. Davis-Stober* Nicholas Brown# |
We present a classification methodology that jointly assigns to a decision maker a best-fitting decision strategy for a set of choice data as well as a best-fitting stochastic specification of that decision strategy. Our methodology utilizes normalized maximum likelihood as a model selection criterion to compare multiple, possibly non-nested, stochastic specifications of candidate strategies. In addition to single strategy with “error” stochastic specifications, we consider mixture specifications, i.e., strategies comprised of a probability distribution over multiple strategies. In this way, our approach generalizes the classification framework of Bröder and Schiffer (2003a). We apply our methodology to an existing dataset and find that some decision makers are best fit by a single strategy with varying levels of error, while others are best described as using a mixture specification over multiple strategies.
Keywords: mixture models, strategy classification, comparative model fit, normalized maximum likelihood, error models, stochastic specification.
Within the decision making literature, there exist many interesting decision theories, both normative and descriptive, that are defined deterministically. These theories, hereafter termed decision strategies, are not defined in terms of random variables and therefore do not explicitly account for fluctuations in choice by a decision maker (DM). Yet, many researchers have observed that DMs are not deterministically consistent in their observed choices across repeated comparisons of the same stimuli set or choice type (e.g., Ballinger & Wilcox, 1997; Busemeyer, Weg, Barkan, Li, & Ma, 2000; Hey, 2001; 2005; Hey & Orme, 1994). This variability of choice does not disappear over repeated experimental sessions for the same subject (e.g., Regenwetter, Dana, & Davis-Stober, 2011) nor can it be attributed entirely to random responses and/or learning and experience effects (Hey, 2001; Loomes, Moffatt, & Sugden, 2002).
Many researchers have suggested different methods of incorporating a stochastic specification to deterministic decision strategies to accommodate variability of choice. Perhaps the simplest stochastic specification is to add a fixed level of “error” to a DM’s responses. This “trembling hand” stochastic specification assumes that a DM follows a single strategy imperfectly with some probability of incorrectly selecting a choice alternative that is not truly preferred (Harless & Camerer, 1994). Other specifications, such as the class of Thurstonian and Fechnerian models, treat preference as deterministic and model choice by adding a random variable representing “noise” (e.g., Böckenholt, 2006). Another class of stochastic specifications are those that incorporate multiple decision strategies with choice modeled as a sampling process over a set of strategies (Loomes et al., 2002; Loomes & Sugden, 1995; Loomes, 2005; Marschak, 1960; Rapoport & Wallsten, 1972; Rieskamp & Otto, 2006). There are, of course, many variations and combinations of the above specifications as well (Loomes et al., 2002). Further complicating matters, the choice of which stochastic specification to use is not an innocuous one. Hey (2005) recently argued that different specifications can lead to different conclusions for the same set of decision strategies and urged that we “should not be silent about noise” when evaluating decision strategies.1
In this article, we present a new strategy classification framework that evaluates a set of candidate strategies over multiple types of stochastic specification. We consider single strategy with “error” specifications as well as probabilistic mixtures of strategies, and, using modern model selection criteria, directly compare these different models to one another retaining the optimal strategy-specification pair for a set of observed choice data. Thus, our framework assigns not only the best-fitting strategy(ies) to a DM’s choices, but also a best-fitting stochastic specification. We illustrate our classification framework with a simulation study that considers three different decision strategies over four types of stochastic specification. We also apply our framework to an existing empirical data set collected to test the transitivity of preference axiom (Tversky, 1969). Throughout this article we will be concerned with the classification of strategies to DMs using outcome-based choice data, a perspective often referred to as comparative model fitting.2
Table 1: Stochastic specifications.
Stochastic specification Description Low-Error Specification A DM strictly adheres to a single strategy and makes an error with a probability no greater than some small value, e.g., .03. This small error rate is assumed to be equal for all choice pairs. High-Error Specification A DM adheres to a single strategy but may commit errors with a single fixed probability no greater than .20. This error rate is assumed to be equal for all choice pairs (e.g., Bröder & Schiffer, 2003a; Harless & Camerer, 1994; Glöckner, 2009). Mixture Specification A specification where all of the choice variability of a DM is explained by switching between multiple strategies, i.e., there are no “errors” made by the DM (e.g., Loomes & Sugden, 1995).
How can one carry out strategy classification via choice data? At the most basic level, a researcher could classify strategies by simply counting the number of times a strategy was in accordance with the observed data, thereby ignoring the problem of stochastic specification altogether (e.g., Marewski, Gaissmaier, Schooler, Goldstein, & Gigerenzer, 2010). However, this “accordance rate” approach can lead to significant biases in strategy classification (Bröder, 2010; Bröder & Schiffer, 2003a; Hilbig, 2010a). Hilbig (2010a; 2010b) demonstrates how these practices can lead to theoretical confoundings and uninterpretable data. Regenwetter et al. (2009) provides a critique of the related practice of evaluating strategies by modal pair-wise majority (e.g., Brandstätter, Gigerenzer, & Hertwig, 2006).
More recent approaches have leveraged statistical models to carry out strategy classification. Bröder and Schiffer (2003a) developed a methodology built on a binomial (multinomial) statistical framework that models DMs as utilizing a single strategy with some fixed probability of making an “error”. Under this framework, strategy classification is likelihood-based and is carried out by calculating and comparing Bayes factor scores (Bröder & Schiffer, 2003a). This basic approach has been successfully applied to memory-based multiattribute choice (Bröder & Gaissmaier, 2007; Bröder & Schiffer, 2003b) and decision making under risk paradigms (Glöckner & Betsch, 2008). Glöckner (2009; 2010) generalizes this approach by incorporating any number of additional measures, such as decision time and confidence data, into the likelihood function to allow theories with identical predictions at the choice level to be distinguished, see also Bergert and Nosofsky (2007) and Glöckner (2006). These approaches share the similar assumption that all DMs utilize the same stochastic specification. To tackle the problem of DMs following different stochastic specifications, Loomes et al. (2002) adapted a non-nested likelihood ratio test (Vuong, 1989) to evaluate a set of candidate strategies under various stochastic specifications. In a comprehensive set of studies, they found that DMs were best fit by a variety of stochastic specifications with a mixture specification of strategies consistent with expected utility yielding an excellent fit to many DMs. The non-nested likelihood ratio test, however, is an asymptotic test that may lack statistical power when applied to small samples (Genius & Strazzera, 2002). Nor does the non-nested likelihood ratio test provide an explicit measure of model complexity.
In this article, we generalize the strategy classification framework of Bröder and Schiffer (2003a) by considering multiple stochastic specifications of decision strategies, including probabilistic mixtures of multiple strategies. While many specifications are possible under our framework, we will restrict ourselves to the three specifications described in Table 1 for the applications in this article. These specifications were chosen for their theoretical relevance to the Tversky data set (Section 4) as well as to showcase the generality of our approach. We apply the latest operationalization of the minimum description length principle, normalized maximum likelihood, to carry out model selection among all strategy-specification pairs (e.g., Myung, Navarro, & Pitt, 2006). Normalized maximum likelihood is an information-theoretic model selection criteria which evaluates models based upon the ratio of a model’s goodness-of-fit to its complexity, adhering to Occam’s razor by favoring the simplest model that provides a good account of the data. The normalized maximum likelihood criteria accurately accounts for the stochastic complexity of a model and is equally valid for both small and large samples.
Similar to many previous approaches (e.g., Davis-Stober, 2009; Iverson & Falmagne, 1985; Myung, Karabatsos, & Iverson, 2005), we model stochastic choice between two choice alternatives a and b as a fixed probability, θab, i.e., the probability that a is chosen over b. If we model each paired comparison in a two-alternative forced choice task as a Bernoulli process then, assuming independence between trials, a DM’s choice responses follow a binomial distribution. Let nab be the number of times the DM chose a over b and let Nab be the total number of times the pair was presented to the DM. Let K be the set of all distinct choice pairs under consideration.3These assumptions give the following likelihood,
| L(θ | n) = |
| Nab nab θabnab (1−θab)Nab−nab, (1) |
where 0<θab<1, ∀ (a,b) ∈ K. To further simplify notation, let θ = (θab)∀ (a,b) ∈ K and n = (nab)∀ (a,b) ∈ K. Note that (1) can easily be extended to ternary choice by using a trinomial distribution, and, more generally, to k-ary choice, where k ∈ ℕ, using the appropriate multinomial distribution.
Let m be the number of distinct decision strategies under consideration. To each candidate strategy we assign a vector, denoted z, that encodes that strategy’s prediction for each choice pair. Thus, each vector z is of size |K| × 1 with coefficients of 1 (predicts a is preferred to b for the respective choice pair), 0 (predicts b is preferred to a for the respective choice pair), or .5 (predicts guessing between a and b).
We model the different strategy-specification pairs under the common likelihood framework of (1) by placing a series of systematic constraints upon the θ parameters. Let Θ denote the parameter space of all possible θ. By placing these models under a common likelihood structure, we are, in a sense, placing these different strategy-specification pairs on a “common ground” and can carry out model selection to find the best account of the data.
Similar to the formulation in Bröder and Schiffer (2003a) and Glöckner (2009), we can conceptualize the parameters of the binomial likelihood (1) as representing “error” terms for individual strategies. Perhaps the simplest such stochastic specification is to assume a single error rate, є, that is equally applied to all choice pairs and is estimated separately for each strategy under consideration. We can model this stochastic specification under our framework by requiring that all of the parameters in θ are a simple function of є and are bounded in a systematic way, such that if the strategy in question, z, predicts that a is preferred to b then the probability of a being chosen over b is (1-є), i.e., θab = (1−є), if b if predicted to be preferred to a then θab = є, and so on for all choice pairs. Therefore, instead of estimating all |K|-many parameters in θ, we need only estimate a single parameter, є. We handle strategies that predict guessing between pairs by forcing the respective θab parameter(s) to be equal to .5.
The error term, є, is the only parameter that accounts for the variability in the DM’s responses under this specification. This raises the question, how much error is reasonable? Or said another way, what constraints should we place on є? For the applications in this article, we distinguish between two cases although many are possible. First, consider a DM that applies a single strategy in a nearly “error-free” fashion. For this low-error case, we bound є to be no larger than some small value; for our applications we chose an upper bound of .03, and thus 0 < є ≤ .03. Here, the DM is assumed to apply the single strategy, z, either deterministically, or, if he does make errors they are quite seldom. For the second “error” specification, we model DMs who apply a single strategy with larger values of error. For this high-error case, we allow є to vary from 0 to .20 (the DM is expected to make an error a maximum of about one in five trials). The latter stochastic specification is better able to account for DM’s choices as it is less constrained than the former, however it is also less parsimonious as it can fit a much wider range of possible observations. It is important to point out that for most applications these bounds must be chosen a priori and be theoretically motivated. It is certainly permissible to make є “unrestricted,” i.e., 0 < є ≤ .50, however this will allow extremely large error rates and, depending on the context, may not be a realistic assumption.
Within the general likelihood framework of (1), it is possible to model other types of single strategy stochastic specifications. One could easily assign independent error terms to each choice pair by considering a separate and independently estimated є value for each distinct θab, denoted єab. This is similar to the stochastic specification used by Sopher and Gigliotti (1993) in their analysis of intransitive preference. This “multiple errors” stochastic specification could be easily incorporated and properly evaluated within our framework.
One of the most general frameworks for modeling multiple strategies is equivalently termed either a random preference model (Loomes & Sugden, 1995; Marschak, 1960) or a distribution-free random utility model (e.g., Davis-Stober, 2009; Falmagne, 1978; Niederée & Heyer, 1997; Regenwetter, 1996; Regenwetter & Marley, 2001). This stochastic specification models both preference and choice as probabilistic, with a DM’s observed choices being governed by a (possibly unknown) probability distribution over a set of strategies. As an example, suppose a DM eats at a restaurant and tends to follow two different strategies. On some days, he wants to spend as little money as possible and orders the cheapest meal on the menu, at other times he chooses by food quality and therefore chooses the more expensive dishes. This DM’s choices could be well-modeled by a probability distribution over these two strategies (choose by price or food quality).
This type of mixture specification has a very nice geometric interpretation within our framework. Let {z1, z2, …, zm} be the vector representations of a set of m strategies to be considered as a mixture specification, i.e., a stochastic specification in which the DM’s choice probabilities are modeled as an arbitrary probability distribution over the m strategies. We can compactly represent the set of all probability distributions over a set of m strategies {z1, z2, …, zm} as the set of all sums,
| wi zi, (2) |
where wi ≥ 0, ∀ i ∈ {1,2,…, m} and ∑i=1m wi = 1.
The weights, wi, are the corresponding probability weights for the mixture distribution over the m many decision strategies. The set of all such sums (sets of probability weights) corresponds to the convex hull of the set of vectors representing the strategies under consideration, thereby defining a convex polyhedron in the appropriate geometric space (Ziegler, 1994). If we consider the points {z1, z2, …, zm} as embedded within the parameter space Θ we obtain a polyhedron such that its interior corresponds to each and every possible probability distribution over the decision strategies {z1, z2, …, zm}. This polyhedron can be uniquely associated with a set of linear inequality constraints on the parameter space Θ. Said another way, given a set of strategies to consider as a mixture specification, we can solve for the linear inequality constraints on the choice probabilities θ that provide necessary and sufficient conditions for these choice probabilities to be represented as a probability distribution over the strategies under consideration.
As an example, assume that K = {(a,b), (c,d)} with θab and θcd as the choice probabilities corresponding to the two choice pairs in K. Consider three decision strategies with z1 = [ 1 1], z2 = [ 0 0], and z3 = [ 0 1]. The mixture specification over all three of these states can be written as the interior of the triangle formed by taking the convex hull of these points in the parameter space Θ. If we were to consider the mixture model of just z1 and z2 its convex hull would simply be the line segment joining these two points in Θ. Figure 1 presents these different mixture specifications plotted within the parameter space Θ along with the respective linear inequality constraints as a function of θab and θcd. This perspective holds generally in that any mixture specification over a finite number of decision strategies can be represented as a polyhedron in the appropriate (possibly high-dimensional) probability space (e.g., Davis-Stober, 2009).
Figure 1: This figure plots the constraints placed on the parameter space Θ for the three-strategy mixture specification over z1, z2, and z3; as well as the two-strategy mixture specification over z1 and z2. 
The researcher must specify a priori which strategies will be considered as mixture specifications.4It is important to point out that under this mixture stochastic specification all choice variability is modeled as substantive “shifts” between different strategies, i.e., there is no “error” or “noise” component. Other types of mixture specifications are possible under our framework. One could model a mixture-error ‘hybrid’ specification, where the mixture specification is combined with the low and high-error specifications, by solving for the appropriate constraints on the θ parameters.
To carry out model estimation for the strategy(ies)-specification pairs, we define the maximum likelihood estimator in the standard way,
| θ := |
| L(θ| n), (3) |
where the parameter space Θ is constrained according to the strategy-specification pair being considered.
If the stochastic specification is either the low or high-error case then θ is constrained to be a function of the single parameter, є, oriented according to the decision strategy being considered, z, and bounded accordingly. For the low and high-error specifications, (3) has a simple closed-form solution (e.g., Bröder & Schiffer, 2003a) with the parameter є estimated as follows,
| є = |
| , (4) |
where zab is the coefficient in z that corresponds to the pair (a,b). Note that the sums are only taken over the elements of z that do not predict guessing. For the low-error specification, let θab = (1 − min{є, .03}) for all choice pairs in z such that a is predicted to be preferred to b, let θab = min{є, .03} for all choice pairs such that b is predicted to be preferred to a, and let θab = .5 if the strategy represented by z predicts guessing between a and b. For the high error specification, we proceed exactly the same way replacing .03 with .20, i.e., if a is predicted to be preferred to b then θab = (1 − min{є, .20}) and so on. It is routine to show that this estimation method yields the solution to (3) for the low and high-error specifications for any choice of z.
For the mixture case, assume that the choice probabilities of Θ are constrained such that they represent the mixture specification (polyhedron) over the strategies under consideration. The solution to (3) for the mixture cases can then be carried out using standard constrained optimization algorithms.5For all of the stochastic specifications described above, the constraints placed on the θ parameters form a closed, convex set, thus the maximum likelihood estimator always exists and is unique (Davis-Stober, 2009).
How can we place the different strategy-specification pairs on an “equal footing” in order to carry out model selection and classification? Unfortunately, traditional model selection methods, such as the Akaike Information Criteria (AIC) (Akaike, 1973) and the Bayesian Information Criterion (BIC) (Schwarz, 1978), are not appropriate in this situation. Conceptually, the problem lies in the fact that the complexity penalty terms of both the AIC and BIC are simple functions of the number of parameters and thus cannot fully measure the parametric complexity of the stochastic specifications we consider. Within our framework, all pairs comprised of the low-error and high-error specifications would have exactly the same complexity (penalty) term for either the AIC or BIC as both cases have only the single free parameter, є. Yet, the high-error case is able to accommodate a much wider range of data and, in fact, contains the low-error specification as a (greatly constrained) special case! If we consider mixture specifications, the AIC and BIC measures further break down as different mixture specifications may have the same “number” of parameters, but different linear inequality constraints on θ will be able to accommodate data in vastly different ways.
To solve this problem, we will make an appeal to the minimum description length principle (Rissanen, 1978). In contrast to many other methods, such as the Bayes factor, the minimum description length principle does not require the assumption of a “true” data generating distribution or process. As argued by Rissanen (2005), this property is a major strength of the minimum description length perspective, especially in cases where determining or estimating a “true” data generating model is difficult or impossible due to a lack of sample size or fundamental understanding of the phenomenon being observed. Rather, in accordance with Occam’s razor, the minimum description length principle states that the best model of a set of data is the one that leads to the most efficient compression of the data. (Grünwald (2005) provides an in-depth introduction and overview.) Several model selection criteria are derived from the minimum-description-length principle. The most general such derivation is the normalized maximum likelihood (NML) criteria (Barron, Rissanen, & Yu, 1998; Rissanen, 2001) and is defined as follows,
| NML = |
| , (5) |
where L(θ|n) is the maximized likelihood for the observed data n and X is the sample space of the model, i.e., the set of all possible data values. For the case of continuous data, the summation operator in the denominator is replaced by an integral. The NML criteria (5) can be described as a ratio of a model’s goodness-of-fit to its complexity with larger values indicating a superior model. The denominator in (5) is defined as the sum of maximized likelihoods for all possible data points, not just the data that were observed. In this way, the denominator accurately measures the stochastic complexity of a model, incorporating both the size of the parameter space as well as functional complexity (Myung, Navarro, & Pitt, 2006). For example, consider two models that provide an equally good fit to a set of observed data. If one of these models fit well many more data points than the other the denominator term in (5) for that model would be quite large and thus, ceteris paribus, the simpler model would be preferred. See Myung, Navarro and Pitt (2006) for a tutorial on the NML criteria.
Table 2: Decision strategies.
Strategy Description Take The Best (TTB) Take The Best is a non-compensatory lexicographic decision strategy in which the DM chooses between choice alternatives by only considering the cue with the the highest validity, if this cue does not distinguish between the alternatives the cue with the next highest validity is considered, and so on (Gigerenzer & Goldstein, 1996). Dawes Rule (DR) Dawes Rule is a compensatory unit-weighting decision strategy in which, for the binary cue case, a DM simply adds up the number of present cues and selects the choice alternative with the largest sum. If two alternatives have the same number of present cues then the DM guesses (Dawes, 1979). Franklin’s Rule (FR) Franklin’s Rule is a variation of DR with the exception that the cues are weighted by their respective validities and then summed with the DM preferring the alternative with the largest sum (Gigerenzer & Goldstein, 1999).
To obtain an NML value for a strategy-specification pair within our framework, we first obtain the maximum likelihood estimate for the observed data, n, via (3) and then use this value to calculate L(θ|n). This forms the numerator of (5). We then carry out this process for all possible data points in the sample space corresponding to (1) for fixed values of Nab. Taking the sum over all of these maximized likelihood terms gives the denominator in (5). We then carry out this process for each strategy-specification pair. Finally, we compare all NML values, selecting the strategy-specification pair with the largest NML value. To summarize, our methodology proceeds as follows:
Calculation of the denominator term in (5) can be computationally difficult. All possible data points can be enumerated when both the number of choice pairs in K and the Nab terms are relatively small, thereby allowing a direct computation of the NML terms. For cases when this is not feasible, estimation of the denominator of (5) can be carried out via Monte Carlo sampling (Preacher, Cai, & MacCallum, 2007). It is important to note that, as the values of Nab and/or the number of choice pairs in K increase, the larger the sample space becomes and therefore the more Monte Carlo random samples that are needed to estimate (5). We used 10,000 samples per strategy-specification pair for the empirical example in this article (Section 4). When using Monte Carlo sampling, it is often easier to estimate the average maximized likelihood value over the sample space and use this value in lieu of the sum in the denominator of (5) (Preacher et al., 2007). This substitution will leave the model ordering unchanged. Throughout this article, we report NML values by taking the natural logarithm of (5).
In this section, we illustrate our methodology with a set of candidate strategies and choice alternatives adapted from Bröder and Schiffer (2003a). We consider the following three decision strategies: Take The Best (TTB) (Gigerenzer & Goldstein, 1996), Dawes Rule (DR) (Dawes, 1979), and Franklin’s Rule (FR) (Gigerenzer & Goldstein, 1999), see Table 2 for descriptions. We consider four choice alternatives each comprised of four binary cues with corresponding validities (denoted v).6These choice alternatives are displayed in Table 3 where “+” or “–” denote the presence or absence, respectively, of a given cue for that choice alternative. We consider two paired comparisons of these four choice alternatives, i.e., |K| = 2 and each choice pair is labeled “Type I” and “Type II” respectively. Table 3 lists the predictions made by these strategies for both choice pairs. We will encode a prediction of alternative a preferred over b as “1” and b preferred over a as “0”. Therefore, z1 = [1 1] is the vector representation of TTB, z2 = [0 0] is the vector representation of DR, and z3 = [0 1] is the vector representation of FR. Again, these decision strategies and cues are chosen for purely illustrative purposes. Our framework can accommodate any decision strategy that makes predictions on binary (or k-ary) choice data.
Table 3: Choice alternatives and decision strategy predictions
Type I Type II Cue Validites a b c d Cue 1 (v =.8) + – + – Cue 2 (v = .7) – + + + Cue 3 (v = .6) – + – + Cue 4 (v = .1) – – – + Strategies TTB a c DR b d FR b c
Figure 2: Classification of the 25 simulated data points under all stochastic specifications for the TTB, DR, and FR strategies. 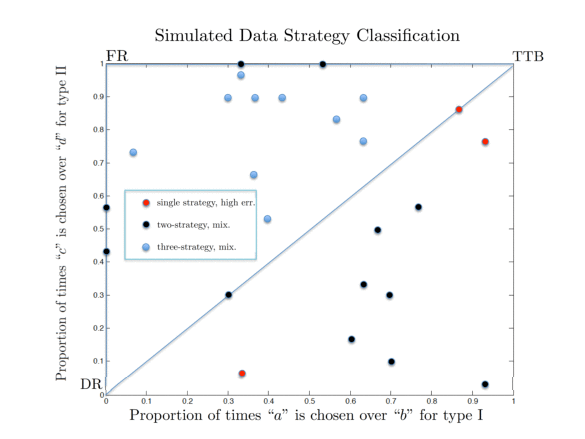
To illustrate how our methodology maps candidate strategy-specification pairs to individual DMs, we simulated data from 25 hypothetical DMs whose “true” choice probabilities, θ, were uniformly distributed over all possible choice probabilities. We carried out our methodology on the three decision strategies considering: both low and high-error specifications for each strategy, all two-strategy mixture specifications, and the single mixture specification over all three strategies. We assumed that each choice type was presented a total of 30 times each. Table 4 lists the NML values for each strategy-specification pair over the 25 simulated data sets. The optimal NML values are in bold. Due to the relatively small sample space, we were able to completely enumerate all possible data points and calculate the NML values exactly. Each data set yielded a unique optimal strategy-specification pair, although several NML values were close in value for some data sets indicating several “good” alternative models. The complexity terms (denominator in (5)) for the single strategy error specifications were approximately .56, both low and high-error specifications differing in the fifth decimal place. The complexity terms for the two-strategy mixture specifications were 2.015 for both {z1, z2} and {z1, z3}, and were 2.014 for {z3, z3}. The three-strategy mixture had a complexity of 3.05. The raw Matlab© code we used for this example is available as supplementary online material (http://journal.sjdm.org/vol6.8.html).
Table 4: NML values for simulated Data.
Sim. Data z1 (low) z1 (high) z2 (low) z2 (high) z3 (low) z3 (high) {z1, z2} {z1, z3} {z2, z3} {z1, z2, z3} {11,20} –74.25 –41.92 –109.01 –55.78 –102.05 –53.01 –112.05 –103.19 –42.26 −39.92 {2,22} –36.01 –26.45 –84.67 –46.08 –126.39 –62.72 –35.04 –75.73 –41.08 −25.86 {0,13} –60.34 –36.38 –46.44 –30.83 –164.62 –77.96 −21.23 –142.22 –32.06 –21.64 {21,3} –168.10 –79.35 –84.67 –46.08 –126.39 —62.72 –185.02 –240.80 −41.08 –41.50 {11,27} –49.91 –32.22 –133.34 –65.49 –77.72 –43.31 –102.99 –45.67 –40.13 −30.58 {19,10} –136.82 –66.87 –102.05 –53.01 –109.01 –55.78 –181.32 –191.81 −42.26 –42.67 {19,23} –91.63 –48.85 –147.24 –71.03 –63.82 –37.76 –174.90 –78.45 –37.35 −37.13 {9,9} –105.53 –54.40 –63.82 –37.76 –147.24 –71.03 –94.08 –199.17 −37.35 –37.77 {18,5} –150.72 –72.42 –81.20 –44.69 –129.86 –64.10 –168.39 –226.23 −40.64 –41.05 {13,27} –56.87 –34.99 –140.29 –68.26 –70.77 –40.53 –119.62 –46.15 –38.89 −31.39 {9,27} –42.96 –29.44 –126.39 –62.72 –84.67 –46.08 –86.71 –44.73 –41.08 −29.19 {16,30} –56.87 –34.99 –161.15 –76.58 –49.91 –32.22 –134.19 −21.43 –33.30 –21.85 {28,23} –122.91 –61.33 –178.53 –83.51 –32.53 −24.78 –254.83 –67.53 –26.06 –26.48 {10,2} –133.34 –65.49 –42.96 −29.44 –168.10 –79.35 –92.34 –249.88 –30.72 –31.14 {0,17} –46.44 –30.83 –60.34 –36.38 –150.72 –72.42 −21.23 –109.74 –36.46 –21.64 {10,30} –36.01 –26.45 –140.29 –68.26 –70.77 –40.53 –85.01 −19.80 –38.89 –20.21 {20,15} –122.91 –61.33 –122.91 –61.33 –88.15 –47.47 –191.81 –146.52 −41.45 –41.87 {26,26} –105.53 –54.40 –182.00 –84.90 –29.06 −22.98 –231.37 –46.64 –24.26 –24.67 {28,1} –199.39 –91.83 –102.05 –53.01 –109.01 –55.78 –241.32 –249.08 −42.26 –42.67 {10,29} –39.48 –28.00 –136.82 –66.87 –74.25 –41.92 –89.66 –28.47 –39.55 −24.59 {19,27} –77.72 –43.31 –161.15 –76.58 –49.91 –32.22 –170.02 –45.67 –33.30 −30.58 {23,17} –126.39 –62.72 –140.29 –68.26 –70.77 –40.53 –210.34 –125.92 −38.89 –39.31 {12,16} –91.63 –48.85 –98.58 –51.63 –112.48 –57.17 –122.29 –139.95 –42.16 −42.03 {21,9} –147.24 –71.03 –105.53 –54.40 –105.53 –54.40 –199.17 –199.17 −42.29 –42.70 {17,25} –77.72 –43.31 –147.24 –71.03 –63.82 –37.76 –155.97 –63.85 –37.35 −35.16
Table 5: BIC values for simulated Data
Sim. Data z1 (low) z1 (high) z2 (low) z2 (high) z3 (low) z3 (high) {z1, z2} {z1, z3} {z2, z3} {z1, z2, z3} {11,20} 153.75 89.10 223.27 116.82 209.36 111.28 226.79 209.07 87.21 85.81 {2,22} 77.27 58.16 174.60 97.41 258.03 130.68 72.77 154.15 84.86 57.68 {0,13} 125.94 78.01 98.13 66.92 334.50 161.18 45.15 287.13 66.81 49.25 {21,3} 341.45 163.96 174.60 97.41 258.03 130.68 372.74 484.30 84.86 88.95 {11,27} 105.08 69.69 271.93 136.23 160.70 91.87 208.67 94.03 82.95 67.12 {19,10} 278.89 139.00 209.36 111.28 223.27 116.82 365.34 386.32 87.21 91.30 {19,23} 188.51 102.96 299.74 147.32 132.89 80.78 352.49 159.58 77.40 80.21 {9,9} 216.32 114.05 132.89 80.78 299.74 147.32 190.85 401.04 77.40 81.49 {18,5} 306.69 150.09 167.65 94.64 264.98 133.46 339.48 455.14 83.98 88.07 {13,27} 118.94 75.23 285.84 141.78 146.79 86.32 241.94 95.00 80.48 68.75 {9,27} 91.18 64.14 258.03 130.68 174.60 97.41 176.12 92.14 84.86 64.35 {16,30} 118.98 75.23 327.55 158.41 105.08 69.69 271.08 45.56 69.29 49.65 {28,23} 251.08 127.91 362.31 172.27 70.32 54.82 512.35 137.76 54.82 58.91 {10,2} 271.93 136.23 91.18 64.14 341.45 163.96 187.36 502.46 64.14 68.24 {0,17} 98.13 66.92 125.94 78.01 306.69 150.09 45.15 222.17 75.62 49.25 {10,30} 77.27 58.16 285.84 141.78 146.79 86.32 172.71 42.29 80.48 46.39 {20,15} 251.08 127.91 251.08 127.91 181.55 100.19 386.32 295.73 85.60 89.69 {26,26} 216.32 114.05 369.26 175.05 63.37 51.22 465.44 95.97 51.22 55.31 {28,1} 404.02 188.91 209.36 111.28 223.27 116.82 485.32 500.86 87.21 91.30 {10,29} 84.22 61.26 278.89 139.00 153.75 89.10 182.01 59.64 81.79 55.15 {19,27} 160.70 91.87 327.55 158.41 105.08 69.69 342.74 94.03 69.29 67.12 {23,17} 258.03 130.68 285.84 141.78 146.79 86.32 423.36 254.54 80.48 84.57 {12,16} 188.51 102.96 202.41 108.51 230.22 119.59 247.27 282.59 87.01 90.02 {21,9} 299.74 147.32 216.32 114.05 216.32 114.05 401.04 401.04 87.27 91.37 {17,25} 160.70 91.87 299.74 147.32 132.89 80.78 314.64 130.40 77.40 76.28
Figure 2 plots the observed choice proportions of the simulated data and labels each point according to the best-fitting strategy-specification pair for those data. The mixture polyhedron(s) are plotted in this space to give the reader a sense of the geometry of the different specifications. It is interesting to note that the amount of choice variability as well as the relative location of the data influence which strategy-specification pair yields the optimal NML value. The structure of the choice variability also plays a large role in determining which stochastic specification best accounts for the data. If the variability is roughly equal across paired comparisons then two-strategy mixture and single state error specifications perform well. If the choice variability is not uniform across paired comparisons then the three-strategy mixture specification tends to perform well.
To illustrate the differences between using NML as compared to traditional model selection criteria, we calculated BIC values for each strategy-specification pair over all 25 simulated data sets.7Table 5 lists these BIC values with optimal values listed in bold, non-unique optimal values are in bold and underlined. The NML and BIC criteria select the same optimal strategy-specification pair for 76% of the simulated data sets. They disagree, however, in two systematic ways. First, several simulated data points are classified as two-strategy mixtures according to BIC, whereas NML classifies them as being best explained via a three-strategy mixture specification. This discrepancy comes from BIC “over-penalizing” the three-strategy mixture by only considering the number of parameters (two in this case) and not taking into account the constraints on that space, as NML does. Said another way, BIC penalizes the three-strategy mixture model as if its parameter space spanned the entire unit square as opposed to spanning only half of it—see Figures 1 and 2. Second, three of the simulated data sets select multiple optimal strategy-specification pairs. In all three cases, a high-error and two-strategy mixture specification have identical optimal BIC values and therefore cannot be distinguished, see Table 5. This problem arises because these two specifications produce identical maximized likelihood values, and, since the BIC criteria considers them equally complex (single parameter models), they are penalized equally. Normalized maximum likelihood, on the other hand, correctly determines that the two-strategy mixture specifications are more complex and thus makes the correct classification.
We applied our methodology to the Tversky (1969) Experiment 1 intransitivity of preference data set. The Appendix contains a detailed description of Tversky’s experimental method as well as the results of our statistical analysis. In summary, we analyzed eight subjects while considering three decision strategies, two transitive and one intransitive. We considered seven possible strategy-specification pairs, including both low and high “error” specifications (є ≤ .03 and є ≤ .20) as well as a mixture specification. We found that Subjects 1 and 6 were best fit by an intransitive strategy with a high-error specification, while the remaining subjects were best fit by a mixture specification over transitive strategies. We conclude that evidence for intransitivity of preference is relatively weak. Our conclusions generally support several previous re-analyses and replications of this experimental paradigm (Birnbaum, 2010; Birnbaum & Gutierrez, 2007; Birnbaum & LaCroix, 2008; Iverson & Falmagne, 1985; Regenwetter et al., 2011). Due to the number of choice alternatives under consideration, we estimated these NML values via Monte Carlo simulation.
In this article, we presented an outcome-based strategy classification methodology that assigns to a DM a best-fitting strategy-specification pair given a set of choice data. Our methodology allows for the evaluation of many stochastic specifications, including probabilistic mixtures of strategies. This methodology is based upon a binomial (multinomial) random variable framework and uses normalized maximum likelihood as a model selection criteria. This methodology generalizes the basic approach of Bröder and Schiffer (2003a) to multiple stochastic specifications using a different model selection criteria. We illustrated our approach using data from a well-known choice experiment and found that some DMs were best fit by a single strategy with “error” specification while others were best fit by a probabilistic mixture over multiple strategies.
While we focused on deterministic decision strategies, this perspective could be applied more generally to stochastic decision theories. Here we refer to theories which explicitly account for choice variability via random variables, stochastic processes, etc. One could simply apply the same NML criteria to any stochastic decision theory that could be estimated via choice data and carry out model selection in a similar fashion. These stochastic theories would not require an additional stochastic specification per se, although multiple stochastic theories could be combined via a mixture process.
For most applications of our framework to real-world data, it is critical to determine the set of strategies and types of stochastic specifications a priori. This leads to two natural questions. First, what decision strategies are reasonable? Fiedler (2010) recently pointed out that, given enough strategies, one could model nearly any decision process. Under our framework, considering a large number of strategies is not necessarily a problem, nor is considering a mixture specification over a large number of strategies as this very complex model would be sufficiently penalized for its ability to accommodate many data sets. However, as with any model selection framework, it is critical that strategies of interest are put up against legitimate competitor candidate strategies and stochastic specifications—not “straw models” to be trivially rejected. Second, what stochastic specifications are reasonable? This will depend upon both the types of decision strategies that the researcher is interested in evaluating as well as the experimental paradigm itself. For example, a researcher may be justified in selecting very large error bounds on single-strategy specifications for an experiment that involves presenting “noisy” unidimensional information to a subject.
There are currently two major limitations of our approach. First, similar to Bröder and Schiffer (2003a), we require all strategies to make distinct predictions, although one could differentiate strategies that made identical predictions based on stochastic specification if theoretically warrented. In this respect, increasing the number of distinct choice pairs can often assist in distinguishing between strategies as this allows more opportunities for different strategies to disagree. Glöckner (2009; 2010) overcomes this limitation within a maximum likelihood classification framework by incorporating additional dependent variables such as decision time and confidence data. Second, calculation of the NML criteria can be very computationally demanding. For large values of |K| and/or Nab, our method estimates the denominator of the NML value via Monte Carlo estimation, which is well-known to have relatively slow convergence rates and does not easily scale up to very high dimensional data. Future work could explore more efficient methods of estimation.
This methodology is well-suited to evaluate how the nature of variability of choice changes over time. It would be possible to consider choice data collected over multiple time points. Given a set of choice data at each time point, our methodology could be used to determine if the best-fitting stochastic specification type, as well as strategy, changes over time. Earlier approaches have found that random “error” tends to dissipate over time with “substantive” shifts of preference, via mixture specifications, remaining (Loomes et al., 2002). Future work could also investigate how our methodology compares with other methods of strategy classification, including “accordance rate” methods.
Akaike, H. (1973). Information theory and an extension of the maximum likelihood principle. In B. N. Petrov, & F. Csáki (Eds.), Second international symposium on information theory (pp. 267–281). Budapest: Akadémiai Kiadó.
Ballinger, T. P., & Wilcox, N. T. (1997). Decisions, error and heterogeneity. The Economic Journal, 107, 1090–1105.
Barron, A., Rissanen, J., & Yu, B. (1998). The minimum description length principle in coding and modeling. IEEE Transactions on Information Theory, 44, 2743–2760.
Bergert, F. B., & Nosofsky, R. M. (2007). A response-time approach to comparing generalized rational and and take-the-best models of decision making. Journal of Experimental Psychology: Learning, Memory, and Cognition, 33, 107–129.
Birnbaum, M. H. (2010). Testing lexicographic semiorders as models of decision making: Priority dominance, integration, interaction, and transitivity. Journal of Mathematical Psychology, 54, 363–386.
Birnbaum, M. H., & Gutierrez, R. J. (2007). Testing for intransitivity of preferences predicted by a lexicographic semi-order. Organizational Behavior and Human Decision Processes, 104, 96–112.
Birnbaum, M. H., & LaCroix, A. R. (2008). Dimension integration: Testing models without trade-offs. Organizational Behavior and Human Decision Processes, 105, 122–133.
Böckenholt, U. (2006). Thurstonian-based analyses: Past, present, and future utilities. Psychometrika, 71, 615–629.
Brandstätter, E., Gigerenzer, G., & Hertwig, R. (2006). The priority heuristic: Making choices without trade-offs. Psychological Review, 113, 409–432.
Brehmer, B. (1994). The psychology of linear judgment models. Acta Psychologica, 87, 137–154.
Bröder, A. (2010). Outcome-based strategy classification. In A. Glöckner & C. Witteman (Eds.), Foundations for tracing intuition: Challenges and methods (pp. 61–82). New York: Psychology Press.
Bröder, A., & Gaissmaier, W. (2007). Sequential processing of cues in memory-based multiattribute decisions. Psychonomic Bulletin and Review, 14, 895–900.
Bröder, A., & Schiffer, S. (2003a). Bayesian strategy assessment in multi-attribute decision making. Journal of Behavioral Decision Making, 16, 193–213.
Bröder, A., & Schiffer, S. (2003b). Take the best versus simultaneous feature matching: Probabilistic inferences from memory and effects of representation format. Journal of Experimental Psychology: General, 132, 277–293.
Brunswik, E. (1952). The conceptual framework of psychology. Chicago: The University of Chicago Press.
Busemeyer, J. R., Weg, E., Barkan, R., Li, X., & Ma, Z. (2000). Dynamic and consequential consistency of choices betweens paths of decision trees. Journal of Experimental Psychology: General, 129, 530–545.
Carbone, E., & Hey, J. D. (2000). Which error story is best? Journal of Risk and Uncertainty, 20, 161–176.
Davis-Stober, C. P. (2009). Analysis of multinomial models under inequality constraints: Applications to measurement theory. Journal of Mathematical Psychology, 53, 1–13.
Davis-Stober, C. P. (2010). A bijection between a set of lexicographic semiorders and pairs of non-crossing Dyck paths. Journal of Mathematical Psychology, 54, 471–474.
Dawes, R. M. (1979). The robust beauty of improper linear models. American Psychologist, 34, 571–582.
Doherty, M. E., & Brehmer, B. (1997). The paramorphic representation of clinical judgment: A thirty-year retrospective. In W. M. Goldstein & R. M. Hogarth (Eds.), Research on judgment and decision making: Currents, connections, and controversies (pp. 537–551). New York: Cambridge University Press.
Falmagne, J.-C. (1978). A representation theorem for finite random scale systems. Journal of Mathematical Psychology, 18, 52–72.
Fiedler, K. (2010). How to study cognitive decision algorithms: The case of the priority heuristic. Judgment and Decision Making, 5, 21–32.
Genius, M., & Strazzera, E. (2002). A note about model selection and tests for non-nested contingent valuation models. Economic Letters, 74, 363–370.
Gigerenzer, G., & Goldstein, D. G. (1996). Reasoning the fast and frugal way: Models of bounded rationality. Psychological Review, 103, 650–669.
Gigerenzer, G., & Goldstein, D. (1999). Betting on one good reason: The take the best heuristic. In G. Gigerenzer, P. M. Todd, & the ABC Research Group (Eds.), Simple heuristics that make us smart, (pp 75–95). New York: Oxford University Press.
Gigerenzer, G., Hoffrage, U., & Kleinbölting, H. (1991). Probabilistic mental models: A Brunswikian theory of confidence. Psychological Review, 98, 506–528.
Glöckner, A. (2006). Automatische Prozesse bei Entscheidungen [Automatic processes in decision making]. Hamburg, Germany: Kovac.
Glöckner, A. (2009). Investigating intuitive and deliberate processes statistically: The multiple-measure maximum likelihood strategy classification method. Judgment and Decision Making, 4, 186–199.
Glöckner, A. (2010). Multiple measure strategy classification: Outcomes, decision times, and confidence ratings. In A. Glöckner & C. Witteman (Eds.), Foundations for tracing intuition: Challenges and methods (pp. 83–105). New York: Psychology Press.
Glöckner, A., & Betsch, T. (2008). Do people make decisions under risk based on ignorance? An empirical test of the Priority Heuristic against Cumulative Prospect Theory. Organizational Behavior and Human Decision Processes, 107, 75–95.
Glöckner, A., & Herbold, A.-K. (2011). An eye-tracking study on information processing in risky decisions: Evidence for compensatory strategies based on automatic processes. Journal of Behavioral Decision Making, 24, 71–98.
Grünwald, P. D. (2005). Introducing the minimum description length principle. In P. D. Grünwald, I. J. Myung, and M. A. Pitt (Eds.). Advances in minimum description length: Theory and applications., (pp 3–22). Cambridge, MA: The MIT Press.
Hammond, K. R., Hursch, C. J., & Todd, F. J. (1964). Analyzing the components of clinical inference. Psychological Review, 71, 438–456.
Harless, D. W., & Camerer, C. F. (1994). The predictive utility of generalized expected utility theories. Econometrica, 62, 1251–1289.
Hey, J. D. (2001). Does repetition improve consistency? Experimental Economics, 4, 5–54.
Hey, J. D. (2005). Why we should not be silent about noise. Experimental Economics, 8, 325–345.
Hey, J. D., & Orme, C. (1994). Investigating generalizations of expected utility theory using experimental data. Econometrica, 62, 1291–1326.
Hilbig, B. E. (2010a). Precise models deserve precise measures: A methodological dissection. Judgment and Decision Making, 5, 272–284.
Hilbig, B. E. (2010b). Reconsidering “evidence” for fast-and-frugal heuristics. Psychonomic Bulletin & Review, 17, 923–930.
Iverson, G. J., & Falmagne, J.-C. (1985). Statistical issues in measurement. Mathematical Social Sciences, 10, 131–153.
Karabatsos, G. (2006). Bayesian nonparametric model selection and model testing. Journal of Mathematical Psychology, 50, 123–148.
Loomes, G. (2005). Modeling the stochastic component of behavior in experiments: Some issues for the interpretation of data. Experimental Economics, 8, 301–323.
Loomes, G., & Sugden, R. (1995). Incorporating a stochastic element into decision theories. European Economic Review, 39, 641–648.
Loomes, G., Moffatt, P. G., & Sugden, R. (2002). A microeconometric test of alternative stochastic theories of risky choice. The Journal of Risk and Uncertainty, 24, 103–130.
Luce, R. D. (1956). Semiorders and a theory of utility discrimination. Econometrica, 24, 178–191.
Luce, R. D. (2000). Utility of gains and losses: Measurement-theoretical and experimental approaches. Mahwah, N. J.: Erlbaum.
Marewski, J. N., Gaissmaier, W., Schooler, L. J., Goldstein, D. G., & Gigerenzer, G. (2010). From recognition to decisions: Extending and testing recognition-based models for multi-alternative inference. Psychonomic Bulletin & Review, 17, 287–309.
Marschak, J. (1960). Binary-choice constraints and random utility indicators. In Arrow, K. J., Karlin, S., and Supper, P., (Eds.), Proceedings of the first Stanford symposium on mathematical methods in the social sciences, 1959, (pp 312–329). Stanford: Stanford University Press.
Myung, J. I., Karabatsos, G., & Iverson, G. J. (2005). A Bayesian approach to testing decision making axioms. Journal of Mathematical Psychology, 49, 205–225.
Myung, J. I., Navarro, D. J., & Pitt, M. A. (2006). Model selection by normalized maximum likelihood. Journal of Mathematical Psychology, 50, 167–179.
Niederée, R., & Heyer, D. (1997). Generalized random utility models and the representational theory of measurement: A conceptual link. In Marley, A. A. J., (Ed), Choice, Decision and Measurement: Essays in Honor of R. Duncan Luce (pp 153–188). Mahway, N. J.: Lawrence Erlbaum.
Payne, J. W., Bettman, J. R., & Johnson, E. J. (1993). The adaptive decision maker. New York: Cambridge University Press.
Preacher, K., Cai, L., & MacCallum, R. (2007). Alternatives to traditional model comparison strategies for covariance structure models. In T. D. Little, J. A. Bovaird, and N. A. Card (Eds.) Modeling contextual effects in longitudinal studies, (pp 33–62). Mahwah, NJ: Lawrence Erlbaum Associates.
Rapoport, A., & Wallsten, T. S. (1972). Individual decision behavior. Annual Review of Psychology, 23, 131–176.
Regenwetter, M. (1996). Random utility representations of finite m-ary relations. Journal of Mathematical Psychology, 40, 219–234.
Regenwetter, M., & Marley, A. A. J. (2001). Random relations, random utilities, and random functions. Journal of Mathematical Psychology, 45, 864–912.
Regenwetter, M., Dana, J., & Davis-Stober, C. P. (2011). Transitivity of preferences. Psychological Review, 118, 42-56.
Regenwetter, M., Grofman, B., Popova, A., Messner, W., Davis-Stober, C. P., & Cavagnaro, D. R. (2009). Behavioral social choice: a status report. Philosophical Transactions of the Royal Society of London B, 364, 833–843.
Rieskamp, J. (2008). The probabilistic nature of preferential choice. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34, 1446–1465.
Rieskamp, J., & Otto, P. E. (2006). SSL: A theory of how people learn to select strategies. Journal of Experimental Psychology: General, 135, 207–236.
Rieskamp, J., Busemeyer, J. R., & Mellers, B. (2006). Extending the bounds of rationality: Evidence and theories of preferential choice. Journal of Economic Literature, 44, 631–661.
Rissanen, J. (1978). Modeling by shortest data description. Automatica, 14, 465–471.
Rissanen, J. (2001). Strong optimality of the normalized ML models as universal codes and information in data. IEEE Transactions on Information Theory, 47, 1712–1717.
Rissanen, J. (2005). Lectures on statistical modeling theory. Available online at www.mdl-research.org.
Schwarz, G. (1978). Estimating the dimension of a model. The Annals of Statistics, 6, 461–464.
Sopher, B., & Gigliotti, G. (1993). Intransitive cycles: Rational choice or random error? An answer based on estimation of error rates with experimental data. Theory and Decision, 35, 311–336.
Starmer, C. (2000). Developments in non-expected utility theory: The hunt for a descriptive theory of choice under risk. Journal of Economic Literature, 38, 332–382.
Stewart, T. R. (1988). Judgment analysis: Procedures. In B. Brehmer, & C. R. B. Joyce (Eds.) Human judgment: The SJT view (pp. 41–74). Amsterdam: North-Holland.
Tversky, A. (1969). Intransitivity of preferences. Psychological Review, 76, 31–48.
Vuong, Q. H. (1989). Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica, 57, 307–333.
Ziegler, G. M. (1994). Lectures on polytopes. Berlin: Springer-Verlag.
In this section, we apply our methodology to a previously published data set examining the fundamental choice axiom, transitivity of preference (Tversky, 1969). A DM is said to be transitive in his or her preferences, if, and only if, for any three choice alternatives (a,b,c), if the DM prefers a to b, and prefers b to c, then the DM must prefer a to c. Transitivity of preference is a necessary assumption for a wide range of normative, prescriptive, and descriptive decision theories (see e.g., Luce, 2000).
In a landmark paper, Tversky (1969) used a lexicographic semiorder decision rule to construct an experimental procedure designed to elicit intransitive choices from his participants. A lexicographic semiorder is a generalization of a semiorder, a mathematical structure first developed by Luce (1956) to model DMs’ preferences in the context of just noticeable differences among stimuli. Davis-Stober (2010) presents a series of relationships between semiorders and lexicographic semiorders within the context of “Dyck paths”, mathematical structures used in coding theory. Under a lexicographic semiorder decision rule, a DM examines pairs of attributes of choice alternatives sequentially, preferring an alternative if, and only if, the difference between a set of attributes exceeds a pre-determined “threshold.” Tversky used this non-compensatory decision rule to design the five gambles8 displayed in Table 6.
For his experiment, Tversky displayed the payoffs of these gambles numerically, with the probabilities displayed graphically as a shaded circle with the volume of the shaded region representing the probability of a win. The key idea is that gambles with similar probabilities of a win, called “adjacent” gambles, such as gambles a and b, are perceptually more difficult to distinguish, thus leading the DM to choose by payoff amount. However, when the DM examines gambles that are “far” apart with regard to probability of a win, such as a and e, the DM would choose by probability. This decision-making process would then yield intransitive preferences, e.g., a preferred to b, b preferred to c, c preferred to d, d preferred to e, but e preferred to a.
Table 6: Tversky’s (1969) Experiment I Gamble Set
a b c d e ($5.00, 7/24) ($4.75, 8/24) ($4.50, 9/24) ($4.25, 10/24) ($4.00, 11/24)
Table 7: NML values for Tversky (1969) Data.
z1 (low) z1 (high) z2 (low) z2 (high) z3 (low) z3 (high) z1, z2 (mix) Subj. 1 –178.50 –71.4737 –303.64 –116.14 –88.1214 -30.26 –54.2994 Subj. 2 –213.26 –81.20 –220.21 –82.30 –195.88 –76.51 -44.53 Subj. 3 –95.07 –33.47 –355.78 –137.16 –81.17 –30.23 -26.89 Subj. 4 –272.39 –103.91 –150.69 –54.58 –206.34 –77.38 -36.23 Subj. 5 –161.12 –60.07 –286.26 –109.03 –185.45 –70.87 -39.14 Subj. 6 –77.75 –26.83 –348.86 –133.82 –32.54 -8.48 –22.71 Subj. 7 –175.02 –66.37 –265.40 –100.38 –185.45 –70.10 -43.44 Subj. 8 –102.02 –37.20 –341.88 –130.87 –157.64 –60.23 -31.01
Tversky (1969) pre-selected 8 out of 18 participants to undergo this experimental design (Experiment I) based on their propensity to make intransitive choices during a short pre-experiment session. Tversky presented all pairwise choices of these five gambles a total of twenty times each to all subjects. Tversky concluded that Subjects 1–6 significantly violated transitivity, operationalized as weak stochastic transitivity, at α = .05. This finding was later overturned by a careful re-analysis of the data by Iverson and Falmagne (1985) with only 1 participant violating transitivity. Regenwetter, Dana, and Davis-Stober (2011) recently developed a mixture model over preference states consistent with transitive strategies and found good empirical support for this model within this choice paradigm. This raises the question, could the other “error” stories we described fit some DMs from Tversky’s data as well as a mixture specification, or better?
In our analysis of the Tversky data, we will consider three candidate strategies and carry out our methodology on a total of seven strategy(ies)-specification pairs. Let z1 be the strategy where a DM prefers the five gambles solely by largest probability, for these particular gambles this is equivalent to choosing by expected value. Let z2 be the strategy where the DM prefers the five gambles solely by largest payoff, this corresponds to a reverse ranking of the gambles compared to z1. Finally, let z3 correspond to the strategy where the DM prefers the gambles according to the particular lexicographic semiorder strategy described by Tversky where all paired comparison predictions are the same as z1 with the exception that the DM prefers choice alternative e to a. To carry out our methodology, we will consider the low (є ≤ .03) and high-error (є ≤ .20) specifications for all three strategies as well as the mixture specification of z1 and z2. Table 7 presents all seven estimated NML values for each of the eight subjects in Tversky’s (1969) Experiment I study. The maximum values of NML for each subject are indicated in bold. These NML values were estimated via Monte Carlo simulation with 10,000 simulated points per strategy/specification pair.
Our re-analysis finds that only two subjects (Subjects 1 and 6) are best fit by the intransitive strategy z3 with the high error stochastic specification. It is not surprising that the high error specification was the best fit for these subjects given their relatively large amounts of choice variability. The remaining subjects were best fit by the mixture specification over the strategies z1 and z2. Said another way, these subjects were best fit by a model in which all choice variability is explained by a probabilistic mixture of the transitive strategies z1 and z2. Note that only two subjects were best fit by an intransitive strategy. This supports the general conclusions of Iverson and Falmagne (1985), Regenwetter et al. (2011), Birnbaum (2010), Birnbaum and Gutierrez (2007), and Birnbaum and LaCroix (2008). For an alternative perspective, see the re-analysis by Karabatsos (2006) using a Bayesian nonparametric methodology. It is also interesting to note that the strategy of choosing solely by payoff, either with low or high error, is soundly rejected for all eight subjects.
In agreement with Regenwetter et al. (2011), we conclude that intransitivity of preference is not well supported by these data and that a mixture model approach provides a better fit. This analysis contrasts somewhat with recent Bayesian analyses of these same data that found support for Tversky’s original conclusions (Karabatsos, 2006; Myung, Karabatsos, & Iverson, 2005). However, the key difference may be that these Bayesian tests focused on testing weak stochastic transitivity and did not consider mixture specifications in their analyses.
This document was translated from LATEX by HEVEA.