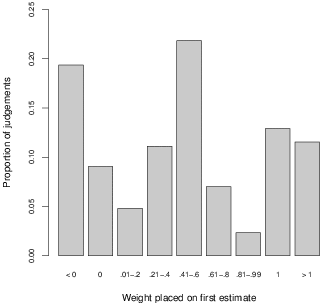
| Figure 1: Aggregate distribution of weight on the first estimate. |
Judgment and Decision Making, vol. 6, no. 4, June 2011, pp. 283-294
Repeated judgment sampling: BoundariesJohannes Müller-Trede* |
This paper investigates the boundaries of the recent result that eliciting more than one estimate from the same person and averaging these can lead to accuracy gains in judgment tasks. It first examines its generality, analysing whether the kind of question being asked has an effect on the size of potential gains. Experimental results show that the question type matters. Previous results reporting potential accuracy gains are reproduced for year-estimation questions, and extended to questions about percentage shares. On the other hand, no gains are found for general numerical questions. The second part of the paper tests repeated judgment sampling’s practical applicability by asking judges to provide a third and final answer on the basis of their first two estimates. In an experiment, the majority of judges do not consistently average their first two answers. As a result, they do not realise the potential accuracy gains from averaging.
Keywords: repeated judgments, judgment accuracy, averaging.
Imagine you have been asked to make a quantitative judgment, say, somebody wants to know when Shakespeare’s Romeo and Juliet was first performed, or you might be planning a holiday in the Alps and are wondering about the elevation of Mont Blanc. An effective strategy to answer such questions is to make an estimate and average it with that of a second judge: a friend, a colleague or just about anybody else (see, for example, Stewart, 2001, or Yaniv, 2004). What, though, if your colleague or friend is unavailable and cannot give you that second opinion? Recent research suggests that you could improve your answer by bringing yourself to make a second estimate and applying the averaging principle to your own two estimates (Herzog & Hertwig, 2009; Vul & Pashler, 2008).
The effectiveness of this suggestion, however, will depend on both the degree to which you are able to elicit two independent estimates from yourself and your willingness to average them. Previous research has focused on the method used to elicit the second estimate. The focus here lies on the type of question being asked, and its interaction with how successive estimates are generated. I report experimental results for different sets of questions which aim to be more representative of quantitative judgments (Brunswik, 1956). I first reproduce previous results which establish the existence of accuracy gains for year-estimation questions such as “In what year were bacteria discovered?” (Herzog & Hertwig, 2009). While I find similar gains for questions about percentage shares (e.g., “Which percentage of Spanish homes have access to the Internet?”), I do not find evidence of accuracy gains for general numerical questions such as “What is the distance in kilometers between Barcelona and the city of Hamburg, in Germany?” or “What is the average depth of the Mediterranean Sea?”. I then investigate whether this difference can be explained by the degree to which answers to the various question types are implicitly bounded, but this hypothesis is not supported by the data.
A second factor is whether judges actually recognise the potential gains from averaging and behave accordingly. Larrick and Soll (2006) argue that people often do not understand the properties and benefits of averaging procedures. My experimental data provide further evidence: only a small minority of judges consistently average their estimates. Often, judges settle for one of their first two judgments as the final answer instead or even extrapolate, providing a final answer that lies outside of the range spanned by their first two estimates. They consequently fail to realise the potential gains from averaging.
Efficiency gains from averaging are pervasive in different contexts and have been discussed extensively in the literatures on forecasting (Armstrong, 2001), opinion revision (Larrick & Soll, 2006) and group judgment (Gigone & Hastie, 1997). The phenomenon is well-understood: averaging leads to accuracy gains as long as the errors inherent in the estimates are at least partly independent (Surowiecki, 2004). Vul and Pashler (2008) and Herzog and Hertwig (2009), using different methods to sample multiple judgments from the same judge, found that averaging these also leads to accuracy gains.
In both of these studies, participants were not aware that they would have to answer the same question multiple times and were asked for their first judgment as a best guess. Vul and Pashler (2008) then simply asked the same person to make the same judgment again. They found an accuracy gain when the second judgment followed immediately, but reported a considerable increase in effectiveness if it was delayed for three weeks. Herzog and Hertwig (2009), on the other hand, proposed a method they called dialectical bootstrapping, which presents judges with instructions on how to make the second judgment, asking them to (i) re-consider their first judgment, (ii) analyse what could have been wrong, and specifically, whether it was likely too low or too high, and (iii) make a second estimate based on these considerations (p. 234). Using this method, they obtained larger accuracy gains than without instructions.
Finally, Rauhut and Lorenz (2011) used yet another elicitation method. In their experiment, participants had to provide five answers to the same question and they were informed about this at the outset. They confirmed Vul and Pashler’s (2008) and Herzog and Hertwig’s (2009) findings of positive accuracy gains from averaging two estimates for four of the six questions they analysed. Furthermore, they found that repeated judgment sampling had diminishing returns: accuracy gains decreased substantially when averaging more than two estimates from the same judge.
Vul and Pashler (2008) interpreted their initial finding as evidence for probabilistic representations of concepts in people’s minds, but nobody has argued that the mechanism underlying repeated judgment sampling is the same as that leading to accuracy gains when averaging different judges’ answers. So far, little is known about how judges generate their different judgments, although some suggestions have been made. Both Vul and Pashler (2008) and Herzog and Hertwig (2009) pointed out the possible role of anchoring-and-adjustment processes, and Rauhut and Lorenz (2011) conjectured that additional judgments may sometimes reflect people becoming emotional or talking themselves into taking wilder and wilder guesses.
A first step toward investigating the processes underlying repeated judgment sampling is to compare its performance in different environments. The experimental study reported below includes different types of questions, including a subset of the year-estimation questions used in Herzog and Hertwig (2009), percentage-share questions, and general numerical questions. I chose the latter two question types because they capture two common types of quantitative judgments judges could face in naturally occurring environments in accordance with representative design (Dhami et al., 2004). In addition, questions about percentage shares are on a response scale which is implicitly bounded between 0 and 100. This allows me to investigate whether the existence of such bounds affects the potential accuracy gains from repeated judgment sampling, as it has been shown to affect performance in other judgment tasks (Huttenlocher et al., 1991; Lee & Brown, 2004).
A second issue is what judges actually do when asked to provide a third answer on the basis of their first two. This is an interesting question given people’s reluctance to employ averaging strategies when combining their own opinion with somebody else’s (Soll and Larrick, 2009), and neither Vul and Pashler (2008) nor Herzog and Hertwig (2009) asked judges to actually give a third estimate. In my analysis, I will distinguish between potential gains from averaging which I compute by taking the average of the judges’ first two answers, and realised gains from their third and final estimates. Whether judges are more likely to average when both judgments are their own than when taking advice from somebody else is important for anyone who thinks of using repeated judgment sampling in actual decisions. In addition, how judges manipulate their previous answers in order to arrive at a third one may enable us to infer something about the processes that underlie the generation of estimates.
I report the results of an experimental study based on a judgment task with two stages. The first stage assesses repeated judgment sampling’s performance in the context of different types of questions. It includes three different question types (within-subject) and either provides explicit bounds for the judges or does not (Bounds vs. No-bounds conditions, between-subject). In the second stage, judges are asked to provide a final estimate on the basis of their first two estimates (Self condition). Judges in a control condition are also given the two answers of a different judge, chosen at random from the participants of the experiment (Other condition). Participants were 82 undergraduate students from the subject pool of the Laboratory for Economic Experiments at Universitat Pompeu Fabra, Barcelona. They received an average payment of 8.70 Euro based on the accuracy (median percentage error) of their answers. Participants came from 16 different academic fields of study, and 58% were female.
The first part of the experiment analyses the effect of the question type on potential accuracy gains from repeated judgment sampling. All gains discussed in this section are like those reported in Herzog and Hertwig (2009), computed by taking the average of participants’ two estimates, and comparing this average to their first answer. They are not “real” gains, since judges were not asked to provide a third answer themselves until the second part of the experiment. The results reported in this section aim to answer the question whether judges could potentially benefit from the method in different environments.
All participants first answered three blocks of twenty questions each (shown in Appendix B). The first block included a sub-sample of the year-estimation questions used in Herzog and Hertwig (2009). It was followed by questions about percentage shares, and the final set of questions consisted of twenty general numerical questions, the answers to which vary by many orders of magnitude. General numerical and percentage share questions were general-knowledge questions, partly sampled from local newspapers.
After completing an unrelated choice task, all participants had to answer the same questions again, in the same order. The elicitation method was adopted from Herzog and Hertwig (2009), and I provided “consider-the-opposite”-type instructions as described above. To further ensure comparability, I also adopted their payment scheme and participants were paid on the basis of the more accurate of the two answers.
Throughout the experiment, subjects in the Bounds condition were also given explicit lower and upper bounds for their answer with each question. For year-estimation items they were told the answer was between 1500 and 1900 and for percentages between 0 and 100. For general numerical questions, the ranges depended on the true unknown value.1 Subjects in the No-bounds condition did not receive this additional information.
Before the analysis, the data were screened for anomalies. The answers of eight participants, five from the Bounds condition and three from the No-bounds condition, were dropped because they were missing a substantial number of answers. The analyses reported below are based on the answers of the remaining 74 (bounds: 28, no-bounds: 46) participants.
Because the distributions of the answers were skewed, the data were transformed to logarithms. Despite this normalisation, the size of the effect depends on the response range for each question. Since these differ considerably across question types, I refrain from estimating general models which include a variable for the question type and its interaction with the condition (Bounds vs. No-bounds). Instead, I compute separate regressions according to Equation 1 for each of the three question types.
| yiq = α + β bi + δi + θq + єiq (1) |
Equation 1 describes a linear regression model with crossed random effects. In this framework, yiq denotes the dependent variable (for the ith individual on the qth question), α is the main effect for gains, β the effect of the explicit bounds provided in the Bounds condition, and δi and θq denote random effects for individuals and questions, respectively. For each of the three question sets, I estimate five such regressions using different dependent variables, measuring the accuracy of the judges’ two estimates and the potential gains judges could obtain from averaging their answers. All of these measures are based on the logarithms of mean absolute deviations of the various estimates from the true value; their algebraic formulae are presented in Table 1.
Table 1: Measures of accuracy and accuracy gain.
Explanation Formula Accuracy of 1st estimate MAD1st = | ln (x1,iq/xtq) | Accuracy of 2nd estimate MAD2nd = | ln (x2,iq/xtq) | Gain from Repeated Judgment Sampling GRJS = | ln (x1,iq/xtq) | − | ln (√x1,iq x2,iq/xtq) | Dyadic Gain GDyad = | ln (x1,iq/xtq) | − 1/N−1 ∑j ≠ i | ln (√x1,iq x1,jq/xtq) | Gain from Average over all judges GWoC = | ln (x1,iq/xtq) | − | ln ((∏i x1,iq)1/N/xtq) |
In Table 1, x1,iq and x2,iq refer to the first and second estimates of judge i for question q, respectively, and xtq refers to the true value for that question. The first two entries in Table 1 are simply logarithms of absolute deviations from the true value.
The bottom three rows in Table 1 describe the different measures for accuracy gains. All three are computed as simple differences in absolute value with respect to the error of the first estimate. A positive coefficient therefore implies an accuracy gain over the first estimate.2 Second, they are all based on geometric means because of the skew of the answers. For repeated judgment sampling (GRJS) the geometric mean is simply the square root of the product of a judge’s two estimates. “Dyadic gains” (GDyad) can be thought of as the expected accuracy gains from averaging with the estimate of a second participant drawn at random. They are computed as the average of the geometric mean of a judge’s first estimate with the first estimate of a second judge. Finally, the estimate from averaging with all other judges at once—the “Wisdom-of-Crowds gain” (GWoC) —is calculated on the basis of the geometric mean across all participants’ first answers. It reflects the accuracy gain a participant could achieve by replacing his own estimate by the (geometric) mean of all participants’ estimates.
Table 2 summarises the results of the analysis. For all three question types, and for both conditions, it provides coefficient estimates for the various accuracy measures discussed. All coefficients reported in Table 2 are significantly different from zero at the one per cent level except for the coefficient for accuracy gains from repeated judgment sampling for general numerical questions (marked by a dagger†), which is not statistically significant.3
Table 2: Accuracy and potential gains by question type and condition.
Year-Estimation Percentage Numerical No-bounds Bounds No-bounds Bounds No-bounds Bounds MAD1 .09 .07 .65 .65 1.8 .50 MAD2 .09 .06 .63 .63 1.8 .51 GRJS .003 .003 .03 .03 .01† .01† GDyad .008 .008 .10 .10 .24 .05 GWoC .019 .019 .23 .23 .61 .16 † All coefficient estimates are significantly different from 0 at the 1% level, apart from the one marked by the dagger which is not significantly different from 0. A coefficient in italics in the bounds condition indicates the absence of a treatment effect, resulting in the same coefficient estimate as in the no-bounds condition.
The results in Table 2 suggest that repeated judgment sampling may not lead to accuracy gains for all types of questions. The first two columns replicate Herzog and Hertwig’s (2009) findings: repeated judgment sampling leads to accuracy gains for year-estimation questions, albeit smaller ones than those which can be expected from averaging one’s estimate with that of another judge, or other judges. These results are confirmed for questions about percentage shares, and the effect is of similar size: accuracy gains from repeated judgment sampling are between a quarter and a third of the size of Dyadic gains, and between an eighth and a tenth of the size of the accuracy gains obtained from averaging all participants’ estimates. For general numerical questions, on the other hand, the picture is different. Averaging with other judges’ answers improves accuracy, but there is no evidence of accuracy gains from repeated judgment sampling for these questions. The coefficient estimate for GRJS is .01, which is 24 times smaller than the estimated coefficient for Dyadic gains and is not significantly different from 0 (p=.67).
Next, consider the effect of the bounds. I hypothesized that the difference between year-estimation, percentage share, and general numerical questions was the degree to which answers to these questions were implicitly bounded. The spectrum ranged from percentage share questions with their implicit bounds between 0 and 100 to general numerical questions, which had no obvious bounds associated with them. Year-estimation questions can be thought of as in between the two extremes, given judges’ familiarity with the Gregorian calendar. The results in Table 2 suggest that the provision of bounds indeed affects judges’ performance differently depending on the question type. They do not support the hypothesis that bounds on the range of possible answers are a sufficient condition for the existence of accuracy gains from repeated judgment sampling, however. As hypothesized, judges’ performance on percentage share questions is not affected by the provision of bounds at all. Bounds slightly improve accuracy for year-estimation questions, but do not effect the potential accuracy gains from the different averaging methods. They have a stronger effect on general numerical questions, with a more pronounced improvement in terms of accuracy, and effects on both Dyadic and Wisdom-of-Crowds gains. Note that these latter effects are negative: bounds reduce the accuracy gain which can be expected from averaging (although first answers are more accurate when bounds are provided, so while the improvement is smaller, it is an improvement over a more accurate first answer). Potential accuracy gains from repeated judgment sampling, on the other hand, are not affected either positively or negatively by the provision of bounds.
Having completed the first part of the experiment, all participants were asked to make a final judgment for a subset of fifteen questions, five for each question type. Participants in the treatment or Self condition had to make this estimate on the basis of their previous two estimates, while these were displayed on screen. The exact instructions they were given were the following: “For the last time, we would like to present you some of the questions which you have answered during this experiment. On the basis of your previous responses, we would like to ask you for a third answer. For this part of the experiment, you will be paid up to 8 Euros, based only on the accuracy of this third and final answer”4. The wording of the instructions was chosen so that participants would have no reason to believe that the subset of 15 answers was selected depending on the accuracy of their previous estimates, and to make clear that only accuracy mattered. In order to avoid priming subjects in a mindset which would make them average less, they were told to give the final answer “on the basis of their previous answers”.
Participants in a control condition (Other) had to make the final judgment on the basis of their own two answers as well as the two answers of a different judge chosen at random among the other participants of the experiment. They did not have any information regarding the order of the two judgments from the second judge. Their instructions were similar: “For the last time, we would like to present you some of the questions which you have answered during this experiment. Here, you can see both your own two previous answers and the two answers of another participant of this experiment, who has been chosen at random. On the basis of this information, we would like to ask you for a third answer. For this part of the experiment, you will be paid up to 8 Euros, based only on the accuracy of this third and final answer.”
Of the 82 participants in the experiment, seven were missing a substantial number of answers and had to be dropped. The analysis reported below are on the basis of the answers of 52 participants in the Self condition and 23 participants in the Other condition. Because of software issues, answers to the last question that was asked were not recorded correctly for a large number of participants, so this item was also excluded from the analysis, restricting the analysis to five year-estimation, five percentage-share and four general numerical questions.
The data from this part of the experiment can be used to answer two questions: How do judges arrive at their third answer?, and: Are third answers actually more accurate than first answers, as repeated judgment sampling suggests? To preview the findings of the analysis, different judges arrive at their final answers differently, but only a small minority of judges average consistently. Final answers are not significantly more accurate than first (or second) answers, and judges do not realise the potential gains from repeated judgment sampling.
As a starting point for the analyses, assume that judges in the self condition arrive at their third judgment by taking a weighted average of their first two estimates. Denoting by ψ the weight placed on the first estimate, their final estimates can then be expressed as in Equation 2, a framework adopted from the literature on opinion revision (Larrick & Soll, 2009):
| x3 = ψ x1 + (1 − ψ) x2 (2) |
The value of ψ can then be calculated separately for each final answer. Note that this method cannot be applied to judges in the Other condition, where the corresponding expression is an equation in three unknowns.5 The Other condition was included as a standard of comparison for the gains judges realise.
Figure 1 shows the distribution of ψ, aggregated over both questions and participants. From the figure, two assertions can be made about judges’ behaviour.
Figure 1: Aggregate distribution of weight on the first estimate. 
The first observation is that judges often extrapolate and provide a final answer outside of the range spanned by their first two answers, as indicated by the left- and rightmost columns in Figure 1. This constitutes a marked difference from the literature on advice-taking and opinion revision, in which estimates outside of the bounds spanned by one’s own estimate and that of the advisor tend to account for less than 5% of answers (Soll & Larrick, 2009; Yaniv & Kleinberger, 2000). In comparison, in the present study such answers account for over 30% of all answers. While in opinion revision, they may be attributed to error and hence disregarded (Yaniv & Kleinberger, 2000), it seems hard to make such an argument in the present case.
A second observation concerns the skew to the left evident in Figure 1. Judges tend to lean more toward their second answer than their first when giving a final answer: 44% of the aggregated judgments lie to the left of the central column in Figure 1, compared to only 33% to its right. This effect is not as strong as the self/other effect in advice-taking (Yaniv, 2004), but in the present context, both answers are one’s own. The skew can also be detected in judges’ behaviour at the individual level. Comparing the number of questions on which a particular judge uses weights with ψ < .4 with the number of questions on which he uses weights with ψ > .6, 60% of judges lean more toward their second estimate, and only 33% lean more toward their first.
What else can be said about how individual judges arrive at their final answers? Do they all behave similarly or are there individual differences? In particular, are there judges who consistently average their first two answers? In order to answer these questions, I compute a second measure which is closely related to ψ. For each answer, I calculate how far a judge deviates from taking an average:
| ψd = | ⎪ ⎪ | ψ − .5 | ⎪ ⎪ |
A reliability analysis shows that ψd is a reliable measure of individual differences, with a standardised Cronbach’s alpha of .85. For each judge, I then calculate the median6 ψd across the 14 questions, the distribution of which is shown in Figure 2. This median characterises judges in terms of how far they deviate from averaging. A median ψd smaller than .1 implies that a judge averages on at least 50% of answers; a median larger than .5 implies extrapolation for at least 50% of answers.
Figure 2: Distribution of judges’ tendency to average. 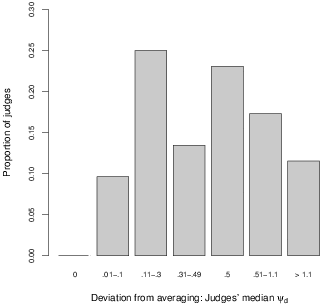
Figure 2 shows that around 10% of judges average consistently, resulting in a median ψd lower than or equal to .1. It also confirms the importance of extrapolations: 28% of judges exhibit a median ψd larger than .5, and therefore extrapolate on more than half of the 14 questions, providing final answers which lie outside of the bounds spanned by their first two estimates. Finally, for almost 25% of judges, the median ψd is exactly .5. This does not imply that 25% of judges consistently settle for either of their first answers as their finale estimate, however, as this figure also includes judges who mix strategies and in addition to sometimes providing one of their previous answers as their third answer, average roughly as often as they extrapolate.
What are the implications for the actual accuracy gains judges were able to realise when making their final estimates? Table 3 shows both the potential gains from averaging, computed as before by taking the average of the judges’ two estimates, and the realised gains, that is, the accuracy gain of the third and final answer over the first answer. Since I show above that there are no potential gains for general numerical questions, I conduct this analysis on the basis of the 10 year-estimation and percentage-share questions only.
Table 3 shows that judges in the Self condition were unable to realise significant accuracy gains. Potential gains, on the other hand, are positive for judges in the Self condition, who could have improved their judgment accuracy by simply averaging their previous estimates. Judges in the Other condition were not able to realise any gains, either, but unlike judges in the Self condition, they would not have reliably benefited from averaging. The coefficient estimate for potential gains is estimated at −.2, and is not statistically different from zero.7 This explains why judges in the Other condition are not significantly more accurate in their final judgments than judges in the Self condition as can be seen in the first column of Table 3.
Finally, do realised gains differ between individuals? Maybe judges who average consistently improve in accuracy, while those who extrapolate do not. To answer this question, I correlate the judges’ median ψd with the average gains they were able to realise for the 10 questions. If judges who average consistently outperform their fellow participants, this correlation should be significantly negative. The analysis does not yield significant evidence that “averagers” do better, however: Spearman’s rank correlation coefficient is estimated at −.13 (p=.34). A more complex analysis could aim to answer the question at the more disaggregated level of individual answers instead, but a regression analysis with crossed random effects finds no significant effect of ψd on the final accuracy gain achieved on a particular question, either. The estimate for the coefficient associated with ψd is −.01 and fails to reach significance (p=.45).
In this paper, I provided new evidence that sampling more than one judgment from the same judge and averaging them can lead to accuracy gains in judgment tasks. For a sub-sample of the questions used in Herzog and Hertwig (2009) which ask judges to estimate the year in which a particular event happened, I replicated their finding of potential gains from repeated judgment sampling. I then confirmed this result for a second set of questions in which judges estimate percentage shares. On the other hand, I showed that repeated judgment sampling does not lead to accuracy gains for a third set of general numerical questions. Finally, I reported experimental data on how judges combine their two estimates when asked to do so, a question not previously addressed in the literature. The majority of judges did not consistently average their answers. In the experiment, they failed to realise the potential accuracy gains from repeated judgment sampling.
The finding that accuracy gains from repeated judgment sampling depend on the question being asked constitutes a challenge to the analogy drawn by Vul and Pashler (2008) and Herzog and Hertwig (2009) between repeated judgment sampling and the so-called “Wisdom of Crowds”. Accuracy gains from repeated judgment sampling behave like those from averaging different people’s estimates for two of the three question sets I examine, but not for the third set of questions. While the source of the accuracy gains in repeated judgment sampling—the averaging principle—is doubtlessly the same as when averaging with somebody else’s estimate, how judges generate their successive estimates remains unclear.
While my data fall short of answering this question, they reveal cues about what might be going on in the judges’ minds. When asked for a third answer, judges often exhibit a reluctance toward averaging their first two answers, and many of them extrapolate outside of the range spanned by their first two answers. This suggests that they may have thought of more information which could be relevant for the question and which they had not considered when giving their previous estimates. Successive answers could then reflect how judges mentally integrate this cumulative information retrieved from memory to make their judgment. This account of repeated judgment sampling is also consistent with the findings that third estimates lean more toward the second, rather than the first estimates, and that the method does not always emulate the “Wisdom of Crowds”. If the variability in the estimates is caused by different pieces of information, judges need at least some knowledge about a question for them to be able to benefit from repeated judgment sampling. On the other hand, even an ignorant judge would benefit from the “Wisdom of Crowds”.
This notion is closely related to Rauhut and Lorenz’s (2011) hypothesis that question difficulty affects potential accuracy gains, as it predicts no accuracy gains for a hard question that a judge does not know enough about. An interesting issue is what would happen for easy questions judges know a lot about, as these could include professional or expert judgments. Would experts benefit from repeated judgment sampling? In this context, note that my findings also qualify Rauhut and Lorenz’s (2011) result that sampling more than two opinions from the same judge is subject to strongly diminishing returns, since all their questions are of the general-numerical type, which are here shown to be the type of questions repeated judgment sampling performs worst on. It is conceivable that, for easy questions, accuracy gains are particularly large, and that returns from sampling more than twice diminish more slowly.
A final consideration concerns the role of the instructions. On the one hand, the effects of Herzog and Hertwig’s (2009) “consider-the-opposite” technique, designed to induce judges to give two independent estimates could have persisted longer than intended and influenced final answers in the present experimental setup. This could have contributed to the judges’ relutance to average their answers, and also to their tendency to extrapolate. On the other, the finding that only a relatively small minority of judges average consistently has implications for the instructions that would have to be provided, were repeated judgment sampling to be used in decision support. Since judges do no average voluntarily, for the technique to be effective, somebody has to average their judgments for them. That judges should be aware of this when asked for their judgments seems reasonable, even inevitable if a judge were to use the technique more than once. Future work should therefore examine the effects of informing judges about the benefits of averaging before eliciting their judgments.
Armstrong, J.S. (2001). Principles of forecasting: a handbook for researchers and practitioners. Kluwer Academic Publishers.
Baayen, R. H., Davidson, D. J., & Bates, D. (2008). Mixed-effects modeling with crossed random effects for subjects and items. Journal of Memory and Language, 59, 390–412.
Baayen, R. H. (2009). languageR: Data sets and functions with “Analyzing Linguistic Data: A practical introduction to statistics”. R package version 1.2. http://CRAN.R-project.org/package=languageR
Brunswik, E. (1956). Perception and the representative design of psychological experiments. University of California Press.
Dhami, M., Hertwig, R., & Hoffrage, U. (2004). The role of representative design in an ecological approach to cognition. Psychological Bulletin, 130, 959–988.
Gigone, D., & Hastie, R. (1997). Proper analysis of the accuracy of group judgment. Psychological Bulletin, 121, 149–167.
Herzog, S., & Hertwig, R. (2009). The wisdom of many in one mind. Psychological Science, 20, 231–237.
Huttenlocher, J., Hedges, J.V., & Duncan, S. (1991). Categories and particulars: Prototype effects in estimating spatial location. Psychological Review, 98, 352–376.
Larrick, R., & Soll, J. (2006). Intuitions about combining opinions: Misappreciations of the averaging principle. Management Science, 52, 111–127.
Lee, P.J., & Brown, N.R. (2004). The role of guessing and boundaries on date estimation biases. Psychological Review & Bulletin, 11, 748–754.
Rauhut, H., & Lorenz, J. (2011). The wisdom of crowds in one mind: how individuals can simulate the knowledge of diverse societies to reach better decisions. Journal of Mathematical Psychology, 55, 191–197.
Soll, J. & Larrick, R. (2009). Strategies for revising judgment: How (and how well) people use others’ opinions. Journal of Experimental Psychology: Learning, Memory, and Cognition, 35, 780–805.
Stewart, T. (2001). Improving reliability of judgmental forecasts. In Armstrong, J. (Ed.), Principles of forecasting: A handbook for researchers and practitioners.
Surowiecki, J. (2004). The wisdom of crowds: Why the many are smarter than the few and how collective wisdom shapes business, economies, socities, and nations. Random House of Canada.
Vul, E., & Pashler, H. (2008). Measuring the crowd within: Probabilistic representations within individuals. Psychological Science, 19, 645–647.
Yaniv, I. (2004). The benefit of additional opinions. Current directions in psychological science, 13, 75-78.
Yaniv, I., & Kleinberger, E. (2000). Advice taking in decision making: Egocentric discounting and reputation formation. Organizational Behaviour and Human Decision Processes, 83, 260–281.
In order to establish the significance of the effects shown in Table 2, I followed a two-step procedure. First, I established whether the experimental manipulation of providing explicit bounds to the participants had an effect on the particular dependent variable y that I was concerned with. Using the lmer() class in R, I estimated models both of the form given in Equation 1, reproduced here again for convenience, and also of the simpler form shown in Equation 3.
| yiq = α + β bi + δi + θq + єiq |
| ỹiq = α + δi + θq + єiq (3) |
I then tested for an effect of the bounds, comparing the two estimated models with an F-test. For those models for which I could reject the Null hypothesis at the five per cent level (all tests for which I could reject the Null were also significant at the one per cent level), I have reported the estimated coefficients of the more complex model described in (1). If the Null could not be rejected, the estimates in Table 2 are based on the simpler model (3) instead.
For both types of models, I then proceeded to test the estimated coefficients for significance in the second step of my analysis. Significance testing in models with crossed random effects is not trivial because the distribution of the test statistic is unclear. I employed a Monte-Carlo simulation approach as put forward by Baayen, Davidson and Bates (2008), using the pvals.fnc() function provided in the languageR package in R (Baayen, 2009). Coefficients which were estimated as being larger (or smaller) than zero on more than 99% of simulation runs are reported as significant (or not) at the one per cent level in Table 2. Results are generally based on 10000 simulation runs. In the one case in which a coefficient was at the border of the one per cent significance level, I increased the number of simulations to 100000.
Tables 4 to 6 display all sixty questions which were used in the experiment, translated from Spanish, and their respective answers. It also includes the bounds provided to subjects in the Bounds condition. The fifteen questions for which judges had to provide third estimates in the second part of the experiment are indicated with daggers†.
The bounds for the general numerical questions were constructed so that in absolute distance to the closest bounds, the distribution of the true values would resemble those of the other two question types. The mean absolute distance to the closest bound, as a percentage of the distance between the lower- and the upper bound is 0.27 for year-estimation, 0.25 for percentage-share, and 0.28 for general numerical questions. The associated standard deviations are 0.16, 0.13 and 0.13, respectively.
Table 4: Year-estimation questions: In what year...
Bounds
Table 5: Percentage-share questions: Which (is the) percentage...
Bounds Question ... of the adult population in Spain who smoke on a daily basis?† ... of the Masters students in the Master in Economics at Universitat Pompeu Fabra in 2010 who are foreigners? ... of votes in Catalunya that CiU obtained in the last general elections? ... of its annual income that an average household in Spain spends on alcohol and tobacco? ... of Spanish homes that have access to the Internet? ... of the adult population in Spain that has completed third-level studies? ... of world GDP comes from the USA and the EU combined? ... of the population of Spain that lives in Catalunya? ... of Internet users connect from China?† ... of the 159 ‘Clasicos’ which have been played in the Spanish league that FC Barcelona has won?† ... of the people who live in Barcelona are 65 years old or older? ... of the Spanish population that earned a yearly income of 6000 Euros or less in 2009?† ... of the Spanish population who would prefer to have a business of their own to being a employee, if they had sufficient resources? ... of civil servants who went on strike in the general strike on June 8th 2010, according to the government? ... of final customers who change their tele-com provider do so primarily to save money? ... of women working in Catalunya who are in executive positions?† ... of the time they spend on-line do Spanish Internet users dedicate to social networks? ... of Spanish women who have suffered from domestic violence at least once in their lives? ... of employees in Spain who knew with certainty that they would lose their jobs during the next six months in June 2010? ... of the adult population in Spain who call their mum at least once when they go on a trip?
Table 6: General numerical questions: How many / What is ...
Bounds
This document was translated from LATEX by HEVEA.