| Figure 1: Number of recognized items by probability of correct choice |
Judgment and Decision Making, vol. 5, no. 4, July 2010, pp. 230-243
When less is more in the recognition heuristicMichael Smithson*. |
The “less is more effect” (LIME) occurs when a recognition-dependent agent has a greater probability of choosing the better item than a more knowledgeable agent who recognizes more items. Goldstein and Gigerenzer (2002) define α as the probability that a correct choice is made on the basis of recognition alone and β the probability that a correct choice is made when both items are recognized (via additional cues). They claim that a LIME occurs if α > β (α > 1/2) and α and β remain constant as the number of recognized items, n, varies. In fact, it can be shown that neither of these parameters generally remains constant as n varies, and neither of them are simple functions of n. Therefore, a new theoretical basis for the LIME is needed. This paper provides mathematical results for understanding when the LIME can occur and elucidates implications of these results. The major findings presented here are as follows:
The primary implication of these results is that the advantage of the recognition cue depends not only on cue validities, but also on the order in which items are learned. This realization, in turn, suggests that research in this area should incorporate a more dynamic focus on learning and memory processes, and the effects of reputational information.
Keywords: recognition heuristic, less is more, choice
In choosing between two items, an agent who recognizes one item but not the other may use this recognition cue to make the choice, whereas one who recognizes both items must use other cues and one who recognizes neither must guess. The “less is more effect” (LIME) occurs when a recognition-dependent agent has a greater probability of choosing the better item than a more knowledgeable agent who recognizes more items. This paper provides some new mathematical results for understanding when the LIME can occur and elucidates implications of these results.
Many researchers investigating the descriptive validity of the recognition heuristic report high usage rates. Goldstein and Gigerenzer (2002) reported a 90% usage rate. Serwe and Frings (2006) found that 88% of their lay and 93% of their amateur samples used the recognition heuristic in choosing tennis match winners. Newell and Shanks (2004) reported 88% usage in a stock-market setting. Pachur and Biele (2007) found that the recognition heuristic accounted for 90% of the forecasts in their study, more than four other candidate mechanisms. Finally, Pohl (2006) observed that additional cue knowledge increased the usage of the recognition heuristic over cases where recognition of an object did not carry any other knowledge with it.
However, empirical evidence for the LIME is equivocal, at least on face value. Goldstein and Gigerenzer (2002), Serwe and Frings (2006), and Scheibehenne and Bröder (2007) are definitely in the “yes” camp, Pohl (2006) finds that the LIME is possible but claims only small effect-sizes, Andersson, Edman and Ekman (2005) and Ayton and Onkal (1997) present “less is as good as more” evidence, and Pachur and Biele (2007) are decidedly in the “no” camp. Simulation studies based on real ecologies lend some support to the prospect of LIMEs (e.g., Goldstein & Gigerenzer, 2002, and Dougherty, Franco-Watkins & Thomas, 2008). Moreover, Schooler and Hertwig (2005) and Pleskac (2007) present simulation results suggesting that imperfect recognition may actually increase the likelihood of a LIME. Matters are further complicated by shortcomings in some of the studies and an apparent lack of consensus on the requirements for a test of the LIME. These exigencies, combined with the results presented in this paper, render the corpus of empirical studies problematic and inconclusive. I shall return to this matter toward the end of this paper.
Goldstein and Gigerenzer (2002) define α as the probability that a correct choice is made on the basis of recognition alone and β the probability that a correct choice is made when both items are recognized (via additional cues). They claim that a LIME occurs if α > β (α > 1/2) and α and β remain constant as the number of recognized items, n, varies. This view has been widely accepted and used as a guide for when to expect the LIME (e.g., Pachur & Biele 2007). Pleskac (2007) concurs with Goldstein and Gigerenzer and makes an analogous claim under conditions of imperfect recognition.
However, Goldstein and Gigerenzer assume that α and β remain constant as the number of recognized items, n, varies. In fact, neither of these parameters necessarily remains constant as n varies, and neither of them is a simple function of n. We shall see demonstrations of these assertions shortly, and indeed Goldstein and Gigerenzer allowed that the assumption is not realistic. We shall see how various modifications of this assumption lead to the absence or presence of a LIME.
A sufficiently rigorous approach to this problem begins by distinguishing between the probability, β, of correctly choosing between pairs of recognized items using the knowledge cue, and the probability, vc, of correctly choosing between any pair of items using the knowledge cue (i.e., vc is the knowledge cue validity). To begin, I will demonstrate that the LIME can occur when α < β. In Table 1 we have 10 items of which 6 are recognized. The left-most column shows the rank of each item on the outcome and the fifth (Cue Rank) column shows their ranks on a knowledge cue to be used for choosing between two recognized items. For purposes of simplification and clarity, throughout this paper I will restrict discussion to a rank-order knowledge cue with no ties.
First, let us determine α. From Table 1, the number of correct choices is the sum of the 0-entries in the “Recog.” column whose ranks is greater (i.e., worse) each of the 1 entries: Cr = 4 + 4 + 3 + 3 + 2 + 1 = 17. The number of incorrect choices is the sum of the 1-entries whose rank is greater than each of the 0 entries: Dr = 4 + 2 + 1 = 7. The result is α = 17/(7+17) = .708.
We use a similar procedure to compute the probability of making a correct choice using the knowledge cue, i.e., the knowledge cue validity vc. The Cc column in Table 1 shows the number of items ranked worse than the item in each row that would be correctly identified by comparing that item’s cue-rank with that of the other items. For example, the first item has cue-rank 1 so by using the cue to compare it with the other 9 items we would correctly choose the first item as the better-ranked. In contrast, the third item has cue-rank 9, so we would make only 1 correct choice in comparing its cue-rank with those of the items that actually are ranked worse. The Dc column shows the corresponding number of incorrect choices. There are Cc = 30 correct and Dc = 15 incorrect choices, resulting in a cue validity vc = 30/(30+15) = .667. Likewise, from the last two columns in Table 1, the probability of choosing correctly between pairs of recognized items by using the knowledge cue is β = Ccr/(Ccr + Dcr) = 14/(14+1) = .933.
Note that vc ≠ β. That is, we have an example of the fact that the probability of making a correct choice between pairs from the 6 recognized items is not the same as the probability of making a correct choice when all 10 items are recognized. Moreover, both α and β can vary depending on the order in which the remaining items are learned (i.e., become recognizable). For example, if the next item learned is item 6 or 10 then the result will be β = .857, whereas if the next is item 3 or 8 then the result will be β = .809. Likewise, if item 6 is learned next α = .714 whereas if item 10 is learned next α = .524. These examples show variation in α and β as n varies, and they demonstrate that both parameters can take different values for alternative collections of recognized items having the same n.
Moreover, there is no generalized relation between the range of possible values of β and vc. Assuming vc ≥ 1/2 (i.e., use any negative cue in reverse), there is always at least one pair of items whose rank-order matches the order of the cue, so that if only those two items have been learned then β = 1. Conversely, if vc < 1 then there is always at least one pair whose rank-order and cue-order are reversed so that if only those two items have been learned then β = 0. By the same argument, α can range from 0 to 1 depending on the order in which items are learned.
Now, we shall build up the probability of making a correct choice between pairs of items in Table 1, initially following Goldstein and Gigerenzer. For those pairs where one item is recognized and the other isn’t, we use the recognition cue and have
| P(correct & untied) = |
| , |
where N is the total number of items and n is the number of recognized items. The probability of a correct choice when both items are unrecognized (i.e., where a guess must be made) is
| P(correct& neither) = |
| . |
Finally, the probability of a correct choice when both items are recognized is
| P(correct& both) = |
| . |
Summing these terms gives Goldstein and Gigerenzer’s (2002) formula. They denote P(correct) by f(n), so using their notation and plugging in the appropriate numbers yields f(n) = .756. Thus, we have the LIME because vc = .667 < f(n) = .756, but we also have α = .708 < β = .933, so we observe that if β is allowed to vary (and thus differ from vc) a LIME can occur when α < β.
When α and β are not constant, not only can the LIME occur when α < β, but the condition α > β does not guarantee a LIME. A counter-example can be constructed by modifying the one in Table 1. Suppose the knowledge cue ranks for the 10 objects are {5,4,3,2,1,6,7,8,9,10}. Then the knowledge cue validity is vc = 35/(35 + 10) = .778. Now suppose the 6 recognized objects have outcome ranks {1,2,3,4,9,10}. Then α = 16/(16 + 8) = .667 and β = 9/(9 + 6) = .6, and α > β is satisfied. However, both α and β are less than vc so no weighted sum of them and 1/2 is going to exceed vc. Indeed, f(n) = .622, so the LIME does not occur. I shall address the issue of how common are occurrences of the LIME when α < β and no LIME when α > β in sections to follow.
Finally, we need to distinguish among various definitions of the LIME. Goldstein and Gigerenzer point out that there are at least three versions: One comparing more and less knowledgeable agents, another comparing performance in different domains, and a third comparing performance as an agent learns new items. The version we have been discussing is the first kind, vc < f(n), which Katsikopoulos (2010) calls the “full experience” LIME. But another is f(n) > f(n+1), which can occur regardless of whether vc < f(n). Let us call this a “local LIME.” The difference between the two is simply that vc = f(N).
The next section of this paper investigates the co-occurrence of the LIME and α < β. The third lays out the conditions under which the LIME can occur under conditions of perfect and imperfect recognition. The fourth deals with the effect of learning items, and there is a brief concluding section. All technical arguments (theorems and proofs) are relegated to the Appendix.
In this section I will demonstrate that the co-occurrence of the LIME and α < β is likely to be quite commonplace. My purpose is twofold: First, to enhance our understanding of their co-occurrence and, second, to develop a perspective that extends our understanding of the LIME and performance of the recognition heuristic generally. To begin, I will alter the Goldstein-Gigerenzer notation by using vr = α and vcr = β. Thus, all cue validities will be denoted by v with an appropriate subscript. Throughout this paper, without much loss of generality, we will limit the treatment of the knowledge cues to a single cue with ranks and no ties.
The Goldstein-Gigerenzer formula for f(n) is
| f(n) = |
| , (1) |
where Qr = (N − n )(N − n − 1). This can be rewritten as
| f(n) = |
| + 1/2, (2) |
where γ r = 2vr−1 and γ cr = 2vcr−1. These γ parameters are Goodman and Kruskal’s gamma coefficient of association. For instance, γ cr = (Ccr−Dcr)/(Ccr + Dcr). Equation (2) shows that deviations of f(n) from 1/2 may be written as a weighted sum of gamma coefficients. It will prove useful at times to interpret the LIME in these terms.
First, substituting (1 + γc)/2 for vc, from equation (2) we may express the LIME as
| γ c < |
| . (3) |
Second, α < β iff γ r < γ cr. Combining this latter inequality with the LIME inequality above and rearranging terms, we satisfy both the LIME and α < β iff
| < γ r < γ cr . (4) |
It is also possible for the LIME to occur even when vr < vc under this condition:
| γr < γc < |
| . (5) |
It certainly is possible for these inequalities to be satisfied under conditions that are quite ordinary. In particular, it can be shown (see Theorem 1 in the Appendix) that when equations (4) or (5) are satisfied if n < N then it is always the case that vc < vcr. This result reveals that the LIME and α < β always can co-occur for some appropriate n if the recognition heuristic moderates the knowledge cue validity so as to increase it within the subset of recognized items. Thus, the knowledge cue “piggy-backs” on the recognition heuristic. Returning to the simple example in the Introduction, we can see that the LIME and α < β co-occur and, indeed, vc = .667 < vcr = .933.
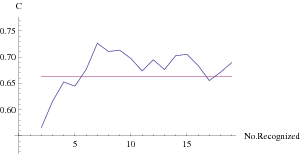
It is all very well to show that the LIME and α < β can co-occur once, but can they repeatedly co-occur as more items become recognized? Suppose we have 20 items ranked 1,2,..., 20 and let the knowledge cue have ranks 2, 5, 10, 12, 19, 20, 4, 6, 3, 9, 8,7 , 1, 14, 13, 11, 15, 18, 17, 16. The knowledge cue validity is vc = .663. Now let the order in which these items become recognized be 1, 3, 7, 4, 6, 12, 14, 2, 19, 18, 9, 15, 20, 5, 8, 11, 10, 13, 16, 17. Figure 1 plots the resulting values for f(n) as items become recognized with vc represented by a horizontal line at .663, with vc < f(n) and therefore the LIME on 12 occasions. Figure 2 plots the cue validity within the recognized items by the recognition validity at each turn. On 10 occasions α < β and 6 of those co-occur with the LIME.
Figure 1: Number of recognized items by probability of correct choice 
Figure 2: Cue validity of recognized items by recognition validity 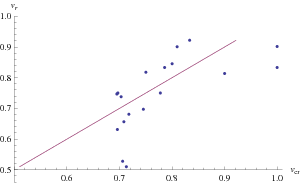
Of course, existence proofs and demonstrations do not indicate whether this co-occurrence is common or not, so let us turn to simulations to pursue this point. The simulations randomly sampled 20 replicates 10,000 times from a trivariate standard normal distribution and converted them to a vector of ranks (x1,x2,x3), where x1 is the outcome rank, x2 is the knowledge cue rank, and x3 is the order of learning rank. The pairwise correlations were set to all possible combinations of {.3, .5, .7}, plus an additional 9 combinations with r13 (the correlation between outcome and order of learning ranks) set to 0, resulting in 36 runs.
Figure 3: P(α<β|vc<f(n)) by r12 and r13 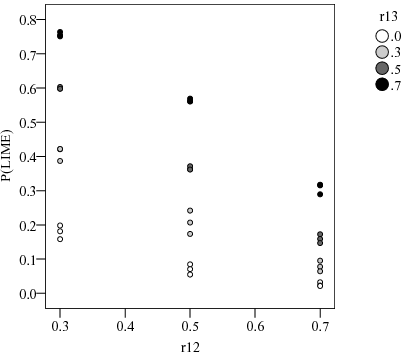
The results are summarized in Figure 3, which displays the proportion of runs where α < β out of those in which vc < f(n), i.e., P(α < β|vc < f(n)). This proportion ranges from about .05 to .43, so this co-occurrence is not uncommon for mid-range cue validities. Moreover, it is apparent that r13, the correlation between outcome and order of learning ranks, drives P(α < β|vc < f(n)). Lower r13 predicts higher P(α<β|vc<f(n)), with the maximum achieved when r13 = 0. In contrast, r12 (the correlation between outcome and the knowledge cue rank) and r23 (the correlation between the order of learning and the knowledge cue rank) have negligible effects. Recall that r13 is a proxy for the cue validity of order of learning which in turn determines the recognition cue validity for each value of n. Therefore, this finding tells us that the co-occurrence of the LIME and α < β is inversely related to the order of learning validity.
We now return to examining the LIME itself. The simulations described earlier may be used to gain intuition about how the LIME is influenced by the cue validities of the knowledge cue and the order of learning, with a “chance” benchmark in which the order of learning is uncorrelated with outcome rank. Figure 4 shows the resulting P(vc<f(n)), the proportion of trials in which the LIME occurred, as a function of r12 and r13. As we might expect, higher r13 predicts a higher probability of the LIME, and for constant r13 a lower r12 predicts more frequent LIMEs. This latter trend reflects the fact that although it is possible for the LIME to occur when α < β, it is easier for it to occur when the opposite is true. As r12 declines it is more likely that α > β and therefore also more likely that the LIME will occur.
Figure 4: P(vc<f(n)) by r12 and r13 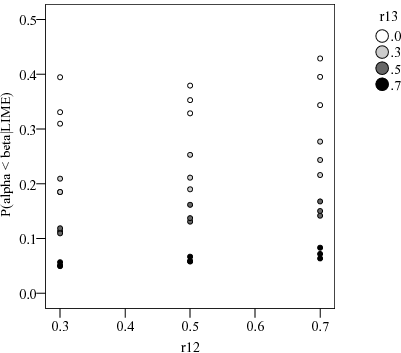
It should be clear that the LIME can occur “by chance,” in the sense that an arbitrary order of learning can sometimes produce the LIME. In the Table 1 example, if item 8 or item 10 is the last item to be learned then just before it is learned f(n) will be .733, both instances of the LIME (recall that vc = .667). However, if item 3 or item 6 is the last to be learned then f(n) will be .644 or .667, neither of which exceeds vc. So, conditional on all items but 3, 6, 8, and 10 having been learned, if each of the remaining four is equally likely to be the last learned then in the last learning stage the probability of the LIME is .5.
Now in Figure 4 note that when r13 = 0, P(vc<f(n)) does not fall to a negligible level. In fact, for r12 = .3 the probability of the LIME is around .15 to .20. It can be driven higher still by allowing a negative correlation between the order of learning and the knowledge cue rank. For r12 = .3 and r23 = −.5, for instance, the simulation resulted in P(vc<f(n)) = .256. At least some occurrences of the LIME are an artifact of random variability in recognition cue validity despite the absence of order-of-learning validity. Therefore, in evaluating the accuracy of the recognition heuristic, it seems advisable to benchmark any empirical findings against appropriate “null” models that track the occurrence of the LIME when the order-of-learning validity is zero.
Is there another general condition restricting when the LIME can occur? This condition can be stated simply but it requires a small addition to the machinery that has been built up so far. Denote by vcnr the probability of choosing correctly between recognized and unrecognized items by using the knowledge cue (rather than the recognition cue), and let vcnn be the probability of correctly choosing between two unrecognized items by using the knowledge cue. Obviously these are “counterfactual” constructions in the sense that the partially ignorant agent cannot use the knowledge cue to choose between items unless both are recognized. Nevertheless, vcnr and vcnn permit us to decompose vc into its three components:
| , |
where again Qr = (N − n )(N − n − 1). From this expression and equation (1) the LIME condition may be written as
| (6) |
This version of the LIME reveals that if vcnn ≥ 1/2 then the LIME occurs only if
| vcnr < vr. (7) |
Recall that in the Goldstein-Gigerenzer notation vr = α. So this really is where the recognition cue’s validity must exceed that of the knowledge cue, namely in choices between a recognized item and an unrecognized item. Schooler and Hertwig’s (2005) implementation of the recognition heuristic in the ACT-R framework uses no knowledge cue and instead assumes guessing when both objects are recognized. That is, they explicitly restrict vcr and vcnn to 0.5 and thus implicitly vcnr also is 0.5. Consequently their simulation obtains a LIME simply by recognition performing above chance level. Conversely, if vcnr ≥ vr the LIME occurs only if vcnn < 1/2. Finally, it should be evident that because vcr (i.e., β) is common to both f(n) and vc, the occurrence of α > β without the LIME may be quite frequent. Indeed, it is no surprise that Pachur and Biele (2007) failed to find a LIME even when the α > β condition was satisfied.
Clearly the order in which items become recognized is crucial in determining whether the LIME will occur. If this order perfectly matches the order of the outcome ranks then of course at each step vr = 1 and the LIME is maximally likely. On the other hand, if pairs of items become recognized whose ranks are equally above and below the median rank then vr = .5 and the LIME is unlikely to occur. The order in which items become recognized acts like another cue with the order of learning determining the ranks of this cue.
Accordingly, let vo denote the validity of the order in which items become recognized. At the point where n items have become recognized we may decompose vo in the same way as vc using an obvious notation, so that we write vo as
| . |
Restrictions on vo impose further restrictions on the conditions under which the LIME occurs. If vo ≤ vc, then vcnr < vr only if γc.r > γo.r, where γc.r is the partial gamma coefficient for the knowledge cue with recognition partialed out and γo.r is the corresponding partial gamma for the order of learning (see Corollary 1 in the Appendix). It may seem counter-intuitive that the LIME could occur even when the order of learning validity is lower than that of the knowledge cue and vcnn ≥ 1/2, but that is unmistakably what this result says. Nor is it difficult to construct such examples.
Table 2 displays one such example with 10 items of which 5 are recognized, vc = .778 < f(n) = .8 and therefore the LIME, and yet vcnn = .6 and vo = .667 < vc. The LIME is achievable here because vcnr = .8 < vr = .88 , and this inequality in turn is achievable because γc.r = .486 > γo.r = .371.
Pleskac (2007) extends the study of the recognition heuristic by introducing a condition that recognition is imperfect, i.e., people do not always recognize the items they have experienced. Thus, instead of just recognized and unrecognized items, there are hits (items correctly identified as having been experienced), misses (items incorrectly identified as not experienced), true rejections (items correctly identified as not experienced), and false alarms (items incorrectly identified as experienced). The result is 10 distinct pairs of items, each with their own decision rule (Pleskac, 2007, Table 1).
Pleskac assumes that the cue validity of experience, denoted by A, is independent of recognition ability, so he replaces α with A. Likewise, he replaces β with B, the validity of the knowledge cue among the experienced (instead of the recognized) items. I have summarized the components of f(n) in his scheme in Table 3, using the abbreviations H for hits, M for misses, T for true rejections, and F for false alarms.
For (M,M), (T,M), and (T,T) pairs a decision maker must guess, so the probability of a correct choice from these three pairs is 1/2. Pleskac (2007: 384) argues that the probabilities of correct choices from the (H,M) and (F,T) pairs also must be 1/2. By definition, the probability of a correct choice from the (T,H) pairs is A, the probability of a correct choice from the (F,M) pairs is 1−A, and the probability of a correct choice from the (H,H) pairs is B.
As Pleskac (2007: 384-5) points out, choices involving the (F,H) pairs benefit partly from experience. Rather than repeating his argument here, suffice it to say that the proportion of correct choices for these pairs is zA+(1−z)/2, where z is the proportion of experienced items that would be chosen over the false-alarm items on the basis of some choice heuristic. In Pleskac’s setup the knowledge cues are binary (either positive or negative) and his version of this heuristic is that the experienced item must have at least one positive cue value. For the time being, we will leave this heuristic unspecified.
Pleskac claims that the LIME can occur only if A > B. In a recent paper Katsikopoulos (2010) disproves this claim, showing that the LIME can co-occur with A < B even allowing Gigerenzer and Goldstein’s assumption. We can extend the argument from section 2 to specify when the LIME can co-occur with A < B. Denoting the hit-rate by h and the false-alarm rate by f, Theorem 2 in the Appendix provides the following characterization of the LIME under imperfect recognition:
| γ c < |
| , (8) |
where ne is the number of items experienced, and γA and γB have the obvious meanings. When h=1 and f=0 (i.e., under perfect recognition) this equation reduces to equation (3) with ne = n, γA = γr, and γB = γcr. Theorem 2 proves that the LIME can co-occur with A < B iff
| < |
| γ A | ⎛ ⎝ | h − f + zhf | ⎞ ⎠ | < γ B | ⎛ ⎝ | h − f + zhf | ⎞ ⎠ | . (9) |
When h=1 and f=0 this equation reduces to equation (4) with the same substitutions as above.
Now, following Katsikopoulos (2010), let
αe = (A − 1/2)(h − f + zhf) + 1/2, and
βe = (B − 1/2)h2 + 1/2.
Thus, αe and βe are analogous to α and β under imperfect recognition. Theorem 2 also shows that the LIME can co-occur with αe < βe iff the γB(h − f + zhf) term in equation (9) is replaced with γBh2. This is a more severe requirement than equation (9), so if the LIME co-occurs with αe < βe it also co-occurs with A < B but the converse does not hold.
A higher value of h and a lower value of f make the inequalities in equations (8) and (9) easier to satisfy, and therefore the LIME more likely to occur. The h − f + zhf term is not positive when f ≥ h/(1−hz), in which case the inequalities cannot hold if γ c, γ B and γ A all are positive. Katsikopoulos (2010) presents a new version of the LIME when f ≥ h/(1−hz), whereby f(n) declines as n increases until n becomes sufficiently large. We will not consider this condition here; a full investigation of the LIME under imperfect recognition is beyond our scope.
Clearly a higher value of z also increases the likelihood of the LIME. Thus, the heuristic driving z when the knowledge cue is ranked instead of binary should be of interest to researchers in this area. A simple heuristic would be to choose the experienced item over the false-alarm item if the knowledge cue rank of the experienced item is better than some benchmark known to the decision maker. On the other hand, a rational decision maker who believes that A > 1/2 should set z = 1.
What form does the general condition for the LIME in equation (7) take under imperfect recognition? To determine this, we begin by assuming that the validity of the knowledge cue differs only across the same three subsets of item pairs as in perfect recognition. This assumption is simply the counterpart of the foregoing assumption regarding the experience cue validity, A, namely that these cue validities are conditionally independent of the agent’s recognition ability. Thus, in Table 4 the knowledge cue validity is B for choices between pairs of experienced items, B1 for choices where one item is experienced and the other not, and B2 when both items are not experienced.
Corollary 2 in the Appendix shows that if the appropriately weighted sum of B2 and B is 1/2 or greater, then the general condition in equation (7) generalizes to the inequality
| γB1 < γA | ⎛ ⎝ | h−f+zhf | ⎞ ⎠ | . (10) |
When h=1 and f=0 this inequality reduces to equation (7) with γA = γr and γB1 = γcnr. As before, higher values of h and z and a lower value of f make this inequality easier to satisfy, and therefore the LIME more likely to occur.
We now will relax the assumption that the experience and recognition are conditionally independent, by allowing the probability of a correct choice between (H,M) pairs to differ from 1/2. This probability is denoted by Q in Table 5. The motivation for relaxing this assumption is to consider the influence that memory effects such as primary or recency might have on the LIME. If the higher-ranked experienced items are more likely to be recognized then Q > 1/2. If the earlier-experienced items are more highly ranked then a primacy effect will result in Q > 1/2, whereas a recency effect would yield Q < 1/2.
Relaxing the conditional independence assumption also affects the probability of a correct choice between (F,M) pairs because the knowledge cue validity for the misses is no longer A. Instead, it is qA, where if Q > 1/2 then 0 < q < 1 whereas if Q < 1/2, q > 1. Corollary 3 in the Appendix shows that the LIME condition in equation (10) generalizes to
| γ B1 | ⎛ ⎝ | N − ne | ⎞ ⎠ | + 2γ B | ⎛ ⎝ | h − h2 | ⎞ ⎠ | ne < |
| γ A | ⎛ ⎝ |
| ⎞ ⎠ | ⎛ ⎝ | N − ne | ⎞ ⎠ | + |
| f | ⎛ ⎝ | 1 − h | ⎞ ⎠ | ⎛ ⎝ | 1 − q | ⎞ ⎠ | ⎛ ⎝ | N − ne | ⎞ ⎠ | + 2γ Q | ⎛ ⎝ | h − h2 | ⎞ ⎠ | ne , (11) |
where γQ = 2Q − 1. For small ne this inequality is dominated by the comparison between γA and γB1, whereas large ne it is dominated by γQ versus γB. Here, the generalized condition for the LIME no longer holds. It is possible for γQ to exceed γB sufficiently to enable the LIME to occur when equation (10) is violated.
In order for a local LIME to occur, f(n) must either rise and then fall or vice-versa. That is, there must be a local “more-is-more” effect (or MIME) followed by a local LIME or vice-versa as items are learned or the reverse sequence if items are being forgotten. There is a corresponding local LIME and MIME pair if we consider removing or adding an item to the collection of items, but we will not deal with that case here. We shall also consider only the case of perfect recognition.
Learning and forgetting items will generally change f(n) but not vc. The conditions under which the direction of change in f(n) can switch sign are of interest, because that is the event that signals a local MIME followed by a local LIME or vice-versa. We will focus on the case where one more item is learned. The results for the case where one item is forgotten differ only in minor respects that are not of interest here.
Let vr1 denote the new probability of correct choices between a recognized and unrecognized pair using the recognition heuristic when one more item has been learned. Likewise, let vcnr1, vcnn1, and vcr1 denote the new probabilities of correct choices using the knowledge cue between a recognized and unrecognized pair, two unrecognized items, and two recognized items respectively. Each of these probabilities will have their corresponding γ parameters as before. Now, consider the change in the proportion of correct choices as one more item is learned: f(n)−f(n+1). Theorem 3 in the Appendix shows that f(n)−f(n+1) = 0 for n < N−1 under the following conditions:
| (12) |
where δr = γr−γr1, δcr = γcr−γcr1, and
| δr0 = |
| . |
When n = N−1, f(n)−f(n+1) = 0 iff
| δcr = |
| . |
For n < (N−1)/2, δr0 > 0 so equation 12 implies that if δr < 0 then δcr > 0. Moreover, even for intermediate values of n ≥ (N−1)/2 it turns out that δr0 is close to 0. Thus, generally equation (12) suggests that in order for a local MIME-LIME sequence to occur, δcr and δr will tend to have opposite signs so that an increase in the recognition validity will be offset by a decrease in the knowledge-cue validity among recognized items and vice-versa.
Now because vc does not change, we also must ascertain the conditions for it to remain constant as one more item is learned. Theorem 4 shows that vc remains constant for n such that n < N−1 under the following conditions:
| (13) |
where δcnr = γcnr−γcnr1, δcnn = γcnn − γcnn1, and
| δcnr0 = |
| . |
When n = N−1, vc remains constant when one more item is learned iff
| δcr = |
| . |
Equation (13) suggests a quasi-hydraulic relation between δcr and both δcnr and δcnn that accords with the commonsense supposition that as an additional item is learned any change in vcr will be compensated by a net opposite change in the weighted sum of vcnr and vcnn due to the fact that vc does not change. For intermediate values of n, it turns out that δcnr0 is close to 0. Consequently, δcnn tends to have a larger effect on δcr than δcnr0 does.
The main results presented in this paper may be summarized as follows.
The results generalize to a binary knowledge cue or an ordinal cue with tied ranks (here I have assumed an ordinal knowledge cue with no tied ranks), and also to a weighted sum of cues. Equivalent examples to those from Table 1 onward using a binary knowledge cue are available from the author on request. Tied ranks sever the analogy with the γ coefficient of association but do not invalidate the results. When the knowledge cue is used to make a choice, I assume guessing is used if the two items are tied on the knowledge cue. Letting Tc denote the number of tied pairs, vc = (Cc + Tc/2)/(Cc + Dc + Tc) and an analogous formula holds for vcr, i.e., β. Now, 2vc − 1 no longer is γc but instead equals Somers’ (1962) dxy, an asymmetric measure of ordinal association (Somers’ measure is related to Kendall’s τb by dxydyx = τb2). Thus, all results in this paper expressed in terms of validities remain as they are, and dealing with ties simply means that all results expressed in terms of γ coefficients have Somers’ dxy substituted for γ.
The findings presented here apply to any binary characteristic whose possession by an item is not fixed but can vary either through assignment by a perceiver or environmental changes. Not only does this include the recognition cue, but any other binary status cue (e.g., membership in a group, organization or club that carries with it relevant knowledge cues and without which those cues are absent). These findings describe how effective status cues earn their keep.
The results also point toward four programmatic recommendations regarding future work on the recognition heuristic. First, despite the demonstrations via analytical results and simulations that α > β is not required for the LIME, it is not known how often α < β and the LIME co-occur in real environments, how often α > β occurs without the LIME, or whether these co-occurrences depend on n and/or N. All three merit further investigation.
Second, the results highlight the importance of the order in which items are learned. No account of the recognition heuristic can be complete without an understanding of the effects of the order of learning, and therefore those aspects of reputational systems and learners determining that order. Population-level models of the recognition heuristic and predictions of its accuracy should incorporate at least an expected order of learning, and preferably an appropriate distributional model of that order.
The implications of these results are compatible with certain other criticisms of empirical research on the recognition heuristic. Dougherty et al. (2008) raise the problem of determining the reference class and ecology within which cue validities are evaluated, and Gigerenzer, Hoffrage and Goldstein’s (2008) response refers to a general confusion between cue validity and ecological validity. The main point is that inferring a LIME via between-agent comparisons requires agents in the same ecology (e.g., German citizens reading German newspapers should not be compared with American citizens reading American newspapers) who are making choices within the same reference class of objects (e.g., f(n) for American cities cannot sensibly be compared with f(n) for German cities).
The results in this paper imply that f(n), α, and β for one set of n recognized objects in a particular ecology and reference class will not necessarily be identical for a different set of n recognized objects, even for the same agent. Moreover, to establish that a LIME has occurred by comparing between agents requires the ecological validity of the knowledge cues to be identical for those agents. Thus, unconfounded between-agent comparisons (agent 1 knows n1 objects and agent 2 knows n2 objects, where n1 > n2) require not only that both agents be located in the same ecology and reference class, but also vc1 = vc2, preferably because both agents use the same knowledge cues in the same way, and the n2 objects are a subset of the n1 objects. Of course, this is unlikely to hold for agents in real environments. For example, Dougherty et al. (2008: 208) suggest that as agents learn more objects they may also learn more effective cues.
The current empirical literature on the recognition heuristic generally is flawed or subject to influences that researchers have not taken into account. For example, Serwe and Frings (2006) compare the predictive accuracy of aggregated rankings of Wimbledon tennis players based on mere recognition with the ATP rankings of these players, so they are not actually evaluating the performance of the recognition heuristic in conjunction with knowledge and guessing. On the other hand, Pohl (2006) and Pachur and Biele (2007) use methods that do this, but the remaining potential confounds in their studies are, first, that the knowledge cue validity vc will be unique for each individual and therefore will have an unknown effect on each person’s β, and second, the sets of objects recognized by subjects whose n is small may not be subsets of the sets of objects recognized by subjects whose n is large.
Within-agent (agent 1 = agent 2) comparisons satisfy nearly all of the aforementioned requirements if the collection of objects remains stable for the duration of the comparisons. Between-agent comparisons or comparisons of mean f(n) for different values of n are vulnerable to confounds except in very restricted or controlled ecologies. A clear recommendation for studying the LIME in its “pure” form with effects due solely to n is tracking agents over time as they learn or forget objects in environments with stable collections of objects.
The order of learning is determined not only by reputational systems but also by learners. The effectiveness of the recognition heuristic therefore hinges not only on aspects of the social environment but also how individuals interact with and learn from that environment, and retain what they have learned. Pleskac (2007) and Katsikopoulos (2010) have made inroads on this topic. Both Katsikopoulos’ paper and the results at the end of section 4 suggest possible joint effects of memory processes (the example used here is primacy versus recency effects) and the reputational system on the performance of the recognition heuristic. Empirical studies would benefit from taking on a more dynamic approach than most recognition heuristic studies, studying how people learn and remember (or forget) about a collection of items.
To date, agent learning or forgetting in regard to the recognition heuristic has been investigated in simulations (e.g., Goldstein & Gigerenzer 1999 and Dougherty et al. 2008) but not empirically. Dougherty et al.’s methods come close to satisfying the requirements for investigating the LIME that have been derived from the results presented here. However, like others in this domain, they have erroneously assumed that β remains constant as n varies and is the same for different collections of n recognized items.
A third direction for future research is the extension of the issues raised in this paper to group inferences. Reimer and Katsikopoulos (2004) present several analytical results characterizing the LIME under various combination rules such as majority-rule. They assume that α and β do not change as n varies, so their findings merit further investigation whereby this assumption is relaxed.
Fourth, collections of items and their ranks on outcomes often are unstable. Ranks can change, of course, because items can improve or decline, even if only through stochastic artifacts such as regression toward the mean. Perhaps more importantly, items may drop out or new ones appear. The disappearance of old items and appearance of novel ones will affect both the order of recognition validity and knowledge cue validity, and therefore the performance of the recognition heuristic. These effects were hinted at but not dealt with here. Understanding them will require the same reorientations described above, namely greater attention to the order in which items are learned (or forgotten), to the joint effects of learner and environment characteristics, and to dynamics in general.
Finally, a few remarks are in order on the limitations and utility of formal analysis as utilized in this paper. As in any mathematization, some idealizations and simplifications have been made. Chief among these is the assumption that the properties of the knowledge cue do not change as more items are learned or forgotten. As Dougherty et al. (2008) observe, it is plausible that this assumption may not hold. On the other hand, the setup in this paper avoids simplifications in earlier analyses that have misguided researchers, most importantly the assumption that α and β are invariant under changes in n or for different collections of n recognized items. I would argue that this new analysis does not commit what Lewandowsky (1993) termed “irrelevant specification.”
Regarding utility, the approach in this paper does what formal analyses and models should (Fum, Missier, & Stocco, 2007). First, it highlights determinants of how the recognition heuristic performs that have been overlooked. It does this by deriving the influence of the order of learning and by introducing “counterfactual” constructs such as vcr, neither of which are obvious in verbal descriptions of the recognition heuristic. Second, it provides guidelines for researchers concerning methods, novel phenomena to investigate, and when the LIME is possible and when it is not.
Andersson, P., Edman, J. & Ekman, M. (2005). Predicting the World Cup 2002 in soccer: Performance and confidence of experts and non-experts. International Journal of Forecasting, 21, 565–576.
Ayton, P., & Önkal, D. (1997). Forecasting football fixtures: Confidence and judged proportion correct. Unpublished manuscript.
Dougherty, M. R., Franco-Watkins, A. M. & Thomas, R. (2008). Psychological plausibility of the theory of probabilistic mental models and the fast and frugal heuristics. Psychological Review, 115, 199–213.
Fum, D., Missier, F., & Stocco, A. (2007). The cognitive modeling of human behavior: Why a model is (sometimes) better than 10,000 words. Cognitive Systems Research, 8, 135-142.
Gigerenzer, G., Hoffrage, U. & Goldstein, D. G. (2008). Fast and frugal heuristics are plausible models of cognition: Reply to Dougherty, Franco-Watkins, and Thomas (2008). Psychological Review, 115, 230–239.
Goldstein, D. G. & Gigerenzer, G. (2002). Models of ecological rationality: The recognition heuristic. Psychological Review, 109, 75–90.
Katsikopoulos, K. V. (2010) The less-is-more effect: Predictions and tests. Judgment and Decision Making, 5, 244–257.
Lewandowsky, S. (1993). The rewards and hazards of computer simulations. Psychological Science, 4, 236-243.
Newell, B. R. & Shanks, D.R. (2004). On the role of recognition in decision making. Journal of Experimental Psychology: Learning, Memory and Cognition, 30, 923-935.
Pachur, T. & Biele, G. (2007). Forecasting from ignorance: the use and usefulness of recognition in lay predictions of sports events. Acta Psychologica, 125, 99-116.
Pleskac, T.J. (2007). A signal detection analysis of the recognition heuristic. Psychonomic Bulletin and Review, 14, 379–391.
Pohl, R. (2006). Empirical tests of the recognition heuristic. Journal of Behavioral Decision Making, 19, 251-271.
Reimer, T. & Katsikopoulos, K. V. (2004) The use of recognition in group decision-making. Cognitive Science, 28, 1009–1029.
Scheibehenne, B. & Bröder, A. (2007). Predicting Wimbledon 2005 tennis results by mere player name recognition. International Journal of Forecasting, 23, 415-426.
Serwe, S. & Frings, C. (2006). Who will win Wimbledon? The recognition heuristic in predicting sports events. Journal of Behavioral Decision Making, 19, 321-332.
Schooler, L. J. & Hertwig, R. (2005). How forgetting aids heuristic inference. Psychological Review, 112, 610-628.
Somers, R. H. (1962). A new asymmetric measure of association for ordinal variables. American Sociological Review, 27, 799-811.
Theorem 1: when equation (4) or (5) is satisfied if n < N then it is always the case that vc < vcr.
Proof: We begin with equation (4). First, we set n = kN and re-express the left-hand inequality in equation (4) as
| = qγ r, |
where 0 < q < 1. Solving for k yields two roots, the relevant one of which is
|
Now, we set γ r = γ, γ c =є γ, and γ cr=δ γ. We also set the restrictions that δ > 1, є > 0, and 0 < q < 1. Setting k < 1, the γ terms cancel out and we get
| <1. |
There are two cases: 2q < δ and 2q > δ. Assuming first that 2q < δ, the above inequality may be rearranged as:
|
Expanding the right-hand side and cancelling common terms on both sides yields
| є < δ. |
Now assuming that 2q > δ, the first inequality may be rearranged as:
|
A similar algebraic argument then leads to є < δ. This requirement immediately implies vc < vcr.
Equation (5) may be rearranged in a similar fashion to solve for k, which yields an identical solution with the additional provisos that q < δ and 0 < є < 1. From the fact that є appears only in the numerator of the root for k tells us that this additional restriction constrains k to lower values than those possible for the co-occurrence of the LIME and α < β, ceteris paribus.
Corollary 1: If vo ≤ vc, then vcnr < vr only if γc.r > γo.r, where γc.r is the partial gamma coefficient for the knowledge cue with recognition partialed out and γo.r is the corresponding partial gamma for the order of learning.
Proof: From the definitions that
| vo = |
|
and
| vc = |
|
it is clear that if vo ≤ vc, then vcnr < vr only if
| vcnnQr + vcr n (n − 1) > vonnQr + vor n (n − 1). |
From the relationship between validities and gamma coefficients, this inequality implies
| γcnnQr + γcr n (n − 1) > γonnQr + γor n (n − 1). |
From the definition of a partial gamma coefficient it follows that
| γc.r = |
|
and
| γo.r = |
| . |
The preceding inequality therefore may be written as
| γc.r > γo.r. |
Theorem 2: the LIME can co-occur with A < B iff
|
| < γ A | ⎛ ⎝ | h − f + zhf | ⎞ ⎠ | < γ B | ⎛ ⎝ | h − f + zhf | ⎞ ⎠ | . |
The LIME also can co-occur with αe < βe iff the γB(h − f + zhf) term in equation (9) is replaced with γBh2. If αe < βe then A < B but the converse does not hold.
Proof:
Constructing f(n) from Pleskac’s Table 1 elements and using the substitutions
A = (γ A + 1)/2 and
B = (γ B + 1)/2,
we may write
| f(n) = |
|
+ 1/2.
From vc = (γ c + 1)/2
we have vc < f(n) iff γc/2 < f(n) − 1/2. Combining A < B with this latter inequality yields
|
| < γ A | ⎛ ⎝ | h − f + zhf | ⎞ ⎠ | < γ B | ⎛ ⎝ | h − f + zhf | ⎞ ⎠ | . |
Now, let
αe = (A − 1/2)(h − f + zhf) + 1/2, and
βe = (B − 1/2)h2 + 1/2.
Then a straightforward algebraic rearrangement of αe < βe yields
γ A(h − f + zhf) < γ Bh2.
The claim that if αe < βe then A < B follows from the observation that
h − f + zhf ≤ h2.
This observation holds because its opposite implies that
h(1−h) < f(zh−1),
which is impossible because the left-hand term is non-negative whereas the right-hand term is non-positive.
Corollary 2: If
|
then vc < f(n) iff
| γB1 < γA | ⎛ ⎝ | h−f+zhf | ⎞ ⎠ | . |
Proof:
Under the inequality specified above and from
Table 3, vc < f(n) iff
|
which may be rearranged to give
| γB1 < γA | ⎛ ⎝ | h−f+zhf | ⎞ ⎠ | . |
Corollary 3: If
|
then vc < f(n) iff
|
where γQ = 2Q − 1.
Proof:
Constructing f(n) from Table 5 and using the substitutions
A = (γ A + 1)/2,
B = (γ B + 1)/2, and
Q = (γ Q + 1)/2,
we may write
|
From vc = (γ c + 1)/2 we get the result immediately.
Theorem 3: For n ≤ N−1, f(n)−f(n+1) = 0 under the following conditions.
For n = N−1,
| δcr = |
| . |
For n < N−1,
| δcr = |
| , |
where
b1 = N−2n−1, b2 = (n+1)(N−n−1),
δcr = γcr−γcr1 and δr = γr−γr1.
Moreover,
δcr < 0 iff δr > δr0 and
δcr ≥ 0 iff δr ≤ δr0,
where
| δr0 = |
| . |
Proof: f(n)−f(n+1) = 0 can be written as a quadratic in n of the form:
| R1n2−R2n+R3 = 0, |
where
R1 = δcr−2δr,
R2 = δcr−2(N−2)δr−2γcr+4γr, and
R3 = 2(N−1)(δr−γr).
This equation is linear in δcr, and a simple algebraic rearrangement yields
| δcr = |
| , |
with b1 and b2 defined as above.
When n = N−1 this equation reduces to
| δcr = |
| . |
Note that the above equation is negative in δr. When n < N−1 setting δcr = 0 and solving for δr yields
| δr = |
| = δr0. |
Thus, for n < N−1,
δcr < 0 iff δr > δr0 and
δcr ≥ 0 iff δr ≤ δr0.
Theorem 4: For n ≤ N−1, the knowledge cue validity remains constant as an additional item is learned, i.e., vc,n−vc,n+1 = 0 (where vc,n denotes the knowledge cue validity when the number of recognized items is n), under the following conditions.
For n = N−1,
| δcr = |
| . |
For n < N−1,
| δcr = |
| , |
where
d1 = N−2n−1,
d2 = N−n−1,
d3 = 2(n+1)(N−n−1),
d4 = 2+N2+3n+n2−N(2n+3),
δcnr = γcnr−γcnr1 and δcnn = γcnn−γcnn1.
Moreover,
δcr < 0 if δcnn > 0 and δcnr = δcnr0,
δcr ≥ 0 if δcnn ≤ 0 and δcnr = δcnr0,
δcr < 0 if δcnr > δcnr0 and δcnn = 0, and
δcr ≥ 0 if δcnr ≤ δcnr0 and δcnn = 0,
where
| δcnr0 = |
| . |
Proof: This proof has the same form as in Theorem 3.
vcn−vcn+1 = 0 can be written as a quadratic in n of the form:
| S1n2−S2n+S3 = 0, |
where
S1 = δcr−δcnn−2δcnr,
S2 = δcr−2N(δcnn−δcnr)+4(γcnr−δcnr) −2(γcr+γcnn), and
S3 = (N−1)(δcnr−γcnr + (N−1)δcnn + 2γcnn).
This equation is linear in δcr, and a simple algebraic rearrangement yields
| δcr = |
| , |
with d1, d2, d3, and d4 defined as above.
When n = N−1 this equation reduces to
| δcr = |
| . |
Note that the above equation is negative in δcnr and in δcnn. When n < N−1 setting δcr = 0 and vc,n−vc,n+1 = 0, and solving these equations for δcnn and δcnr, yields δcnn = 0 and
| δcnr = |
|
| = δcnr0. |
Thus, for n < N−1,we obtain the inequalities in Theorem 4.▫
This document was translated from LATEX by HEVEA.