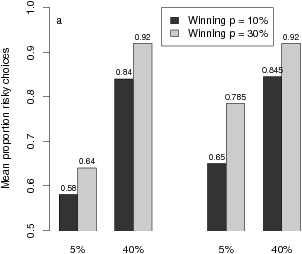
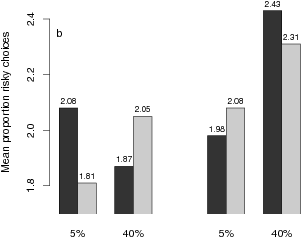
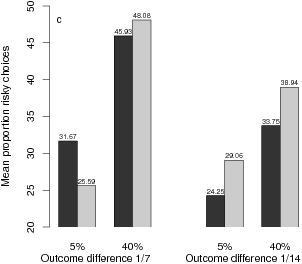
| Figure 1: Mean proportions of risky choices (a), mean difficulty ratings (b), and mean pricing index (c) as a function of experimental conditions. |
Judgment and Decision Making, vol. 5, no. 1 February 2010, pp. 21-32
How to study cognitive decision algorithms: The case of the priority heuristicKlaus Fiedler* |
Although the priority heuristic (PH) is conceived as a cognitive-process model, some of its critical process assumptions remain to be tested. The PH makes very strong ordinal and quantitative assumptions about the strictly sequential, non-compensatory use of three cues in choices between lotteries: (1) the difference between worst outcomes, (2) the difference in worst-case probabilities, and (3) the best outcome that can be obtained. These aspects were manipulated orthogonally in the present experiment. No support was found for the PH. Although the main effect of the primary worst-outcome manipulation was significant, it came along with other effects that the PH excludes. A strong effect of the secondary manipulation of worst-outcome probabilities was not confined to small differences in worst-outcomes; it was actually stronger for large worst-outcome differences. Overall winning probabilities that the PH ignores exerted a systematic influence. The overall rate of choices correctly predicted by the PH was close to chance, although high inter-judge agreement reflected systematic responding. These findings raise fundamental questions about the theoretical status of heuristics as fixed modules.
Keywords: lotteries, non-compensatory heuristics, aspiration level,
risky choice.
For almost four decades, theoretical and empirical work on judgment and decision making has been inspired by the notion of cognitive heuristics. Accordingly, people rarely try to utilize all available information exhaustively, making perfectly accurate judgments. They are usually content with non-optimal but satisficing solutions (Simon, 1983). The cognitive tools that afford such satisficing solutions are commonly called heuristics. Their reputation has improved enormously. Having first been devalued as mental short-cuts, sloppy rules of thumb, and sources of biases and shortcomings, in the more recent literature heuristics are often characterized as fast, frugal, and functional. “Simple heuristics that make us smart” (Gigerenzer, Todd and the ABC research group, 1999; Katsikopoulos et al. 2008) were shown to outperform more ambitious models of rational inference in simulation studies (Gigerenzer & Goldstein, 1996). Yet, in addition to the mathematical proof and simulation that heuristics may perform well when they are applied, the crucial psychological assumption says that decision makers actually do use such heuristics, which are sometimes explained as reflecting phylogenetic, evolutionary learning (Cosmides & Tooby, 2006; Todd, 2000).
Although correlational evidence for the correspondence of a simulated heuristic and a validity criterion is sufficient to study the first (functional) aspect, hypothesis testing about the actual cognitive process supposed in a heuristic calls for the repertoire of experimental cognitive psychology. Thus, for a crucial test of the assumption that judgments of frequency or probability actually follow the availability heuristic (Tversky & Kahneman, 1973), it is essential to manipulate its crucial feature, namely the ease with which information comes to mind. Likewise, for a cogent test of the anchoring heuristic (Tversky & Kahneman, 1974), it has to be shown that judges actually adjust an initial extreme anchor insufficiently. Without appropriate experimental manipulations of the presumed mental operations, it is impossible to prove the causal role of the hypothesized heuristic process. The percentage of a focal heuristic’s correct predictions of judgments or decisions cannot provide cogent and distinct evidence about the underlying process (Hilbig & Pohl, 2008; Roberts & Pashler, 2000).
In the early stage of the heuristics-and-biases research program, though, serious experimental attempts to assess the postulated cognitive operations had been remarkably rare. Hardly any experiment had manipulated the ease of a clearly specified retrieval operation supposed to underlie the availability heuristic (some exceptions were Schwarz et al., 1991, and Wänke & Bless, 2000) or the gradual adjustment process supposed to underlie the anchoring heuristic (Fiedler et al., 2000).1 More recently, though, this situation has been changing. A number of fast and frugal heuristics have been specified precisely enough to allow for strict experimental tests of underlying cognitive processes. Tests of the Take-the-Best heuristic (Gigerenzer et al., 1999) have been concerned with the assumption that cues can be ordered by validity (Bröder & Schiffer, 2003; Newell et al., 2004; Rieskamp & Otto, 2006). Research on the recognition heuristic tested whether comparative judgments are really determined by mere exposure rather than a substantive evaluation of the comparison objects (Hilbig & Pohl, 2008). It seems fair to conclude that strict empirical tests have resulted in a more critical picture of the validity and scope of the postulated heuristics (Dougherty, Franco-Watkins, & Thomas, 2008; but see Gigerenzer, Hoffrage, & Goldstein, 2008).
The present research aims to test the cognitive-process assumptions underlying another heuristic that was recently published in prominent journals, the priority heuristic (PH). The PH (Brandstätter, Gigerenzer & Hertwig, 2006, 2008) constitutes a non-compensatory heuristic that compares decision options on only one cue dimension at a time, rather than trying to integrate compensatory influences of two or more cues. The PH affords an algorithm for choosing between two outcome gambles or lotteries. It consists of three successive steps, concentrating first on the worst outcomes, then on the likelihood of the worst outcomes, and finally on the best possible outcome.2
Specifically, let A and B be two lotteries, each with a maximal outcome, omaxA, omaxB and a minimal outcome ominA, ominB, with corresponding probabilities p(omaxA), p(omaxB), p(ominA), and p(ominB), respectively. Let A for convenience always be the risky lottery with the lowest possible outcome, ominA < ominB. Then PH involves the following three steps:
(1) Consider first the difference in worst outcome ominB – ominA. Choose B and truncate the choice process if the worst-outcome difference in favor of B is larger than 1/10 of the overall maximum (i.e., of both omaxA and omaxB).
(2) If no choice in terms of clearly different worst outcomes is possible, consider next the worst-outcome probabilities, p(ominA), and p(ominB). Truncate the process if the worst-outcome probabilities differ by at least 1/10. In that case, choose the lottery with the lower p(omin); otherwise proceed to the third stage.
(3) Choose the lottery with the higher maximum outcome by comparing omaxA and omaxB. Otherwise guess randomly.
How to test the PH model. Although the PH relies on very strong and specific, hierarchically ordered assumptions about cue priority, truncation rules, and quantitative parameters (i.e., the critical 1/10 factor, called aspiration level, Simon, 1983), it is supposed to be generally applicable to gambles in any content domain. Brandstätter et al. (2006) explicitly propose the PH as a model of the actual cognitive process informing risky choices, assuming that the three cues of the PH, omin, p(omin), and omax, are used in a strictly sequential, non-compensatory way, with only one cue active at each process stage.3 Although Brandstätter et al. (2006) provide choice and latency data to support the PH’s process assumptions, other empirical tests (Ayal & Hochman, 2009; Birnbaum, 2008a; Gloeckner & Betsch, 2008; Hilbig, 2008) suggest that PH assumptions may be hard to maintain. The assumption of a strictly sequential use of singular cues was tackled and refuted by Hilbig (2008) and by Birnbaum (2008a), who found PH-incompatible cue interactions. Ayal and Hochman (2009) showed that reaction times, choice patterns, confidence level, and accuracy were better predicted by compensatory models. Johnson, Schulte-Mecklenbeck, and Willemsen (2008) complained the paucity of process data obtained to substantiate the PH assumptions. However, in spite of this growing evidence, no experiment so far has directly manipulated the aspiration levels of the three-step PH decision process, which together make up the design of the present study. While this is certainly not the only possible way to test the PH, the following considerations provide a straightforward test of its core assumptions.
First, if the initial step involves a comparison of ominB – ominA with 1/10 of the maximal outcome, it is essential to manipulate maximal outcomes to be either smaller or larger than 1/10 of that difference. In the study reported below, the worst-outcome difference factor varies such that ominB – ominA is either 1/7 or 1/14 of omaxA. If the primary PH process assumption is correct, people should uniformly (or at least mostly) choose B in the 1/7 condition. No other factors should influence the decision process in this condition. In particular, no probability should be considered. Even when, say, p(omaxA) is very high, or p(omaxB) is very low, this should be radically ignored if PH assumptions are taken seriously.
Second, for a critical test of the next process step, which should only be reached for worst-outcome differences of 1/14, it is necessary to manipulate the worst-case probability difference, p(ominB) – p(ominA), to be either greater or smaller than 10% (i.e., 1/10 of the possible range of p). Specifically, we manipulate this difference to be +5% versus +40%. If, and only if, p(ominB) and p(ominA) do differ by 40% (i.e., more than 1/10), lottery A should be uniformly chosen. Otherwise, if the worst outcome of B is not clearly more likely than the worst case of A, people should proceed to the third step.
In this final step, the lottery with the higher maximum outcome should be chosen, regardless of all other differences between A and B. Neither the cues considered earlier during the first two steps nor any other aspect of the lotteries should have any influence. For a step-3 test of the strong single-cue assumption, it is appropriate to manipulate one other plausible factor that is irrelevant to the PH. Specifically, we manipulate the overall winning probability for p(omaxB) to be either small or moderate (10% or 30% + increments). According to PH, this irrelevant factor should never play any role for the preference decision. Because p(omaxB) = 1 – p(ominB) and p(omaxA) = 1 – p(ominA), the remaining probability p(omaxA) is equal to p(omaxB) plus the same difference (i.e., 5% or 40%) that holds between p(ominB) – p(ominA).
Such an experiment, to be sure, provides ample opportunities to falsify the PH model: Participants may not uniformly choose B at step 1 when the worst outcome difference is 1/7 of the maximal outcome. Other factors or interactions thereof may influence the choice even when the primary worst-case difference is large enough for a quick step-1 decision. At step 2, people may not choose A if the worst-case probability difference is marked (.40). Rather, the manipulation of p(ominB) – p(ominA) may interact with other factors, contrary to the single-cue assumption of a non-compensatory heuristic. Similarly, at step 3, many people may not choose the option with the highest outcome, or a tendency to do so may interact with the baseline winning probability, or any other factor. While the long list of possible violations of the PH algorithm may appear too strict and almost “unfair”, it only highlights how strong and demanding a process model the PH represents. Rather than protecting the PH from strict tests, my strategy here is to test it critically, taking its precise assumptions seriously. However, such an exercise may yield results that are more generally applicable.
It is worthwhile reasoning about an appropriate sampling of test cases. In prior publications, PH proponents have referred to often-cited choice sets (e.g., Lopes & Oden, 1999; Tversky & Kahneman, 1992) and extreme cases like the Allais (1979) paradox to substantiate the viability and validity of the heuristic. Critiques (Gloeckner & Betsch, 2008; Hilbig, 2008) have applied the PH to randomly constructed tests that were not meant to represent an explicitly defined universe of lotteries or gambles. The stimulus sampling for the present research is guided by the following rationale.
Many economic, social, or health-related decisions involve a trade-off between risk and payoff. To increase one’s payoff or satisfaction, one has to accept an elevated risk level. Accordingly, pairs of lotteries, A and B, were used such that A leads to a high payoff in the fortunate case, whereas in the unfortunate case A’s payoff is lower than in the worst case of a less risky lottery B, which has a flatter outcome distribution. Lotteries that fit this scenario are generated from different basic worst outcomes (i.e., 20,30; 10,80; 80,90; 30,60 for ominA and ominB, respectively), to which a small random increment (chosen from a rectangular distribution of natural numbers from 1 to 10) is added to create different versions. The maximum outcome omaxA is then either 7 times or 14 times as large as the worst outcome difference ominB – ominA. The other lottery’s maximum outcome, omaxB, is set to omaxA · ominA/ominB so that B’s relative advantage in the worst case is proportional to a corresponding disadvantage in the fortunate case. Next the baseline probability p(omaxB) for a success on the non-risky lottery B, p(omaxB), is set to a starting value (either 10% or 30%, again plus a rectangular random increment between 1% and 10%); the complementary probability p(ominB) = 1 – p(omaxB) holds for the unfortunate outcome of B. For the risky option A, a probability increment (either 5% or 40%) is added to the fortunate outcome, p(omaxA) = p(omaxB) + increment, to compensate for A’s disadvantage in omin, while the same decrement is subtracted from the unfortunate outcome, p(ominA) = p(ominB) – increment.
The resulting lotteries (see Appendix A) are meant to be representative of real life trade-offs between risk and hedonic payoff. No boundaries are placed on the ratio of the two options’ expected values (EV). Yet, regarding Brandstätter et al.’s (2006, 2008) contention that the PH functions well only for gambles of similar EV, it should be noted that three of the four worst-outcome starting pairs (20,30; 80,90; 30,60) produce mainly EV ratios well below 2. Only 10,80 tasks often yield higher EV ratios in the range of 2 to 6. In any case, the lotteries’ EV ratio will be controlled in the data analysis as a relevant boundary condition.
Participants and design. Fifty male and female students participated either for payment or to meet a study requirement. They were randomly assigned to one of two questionnaires containing different sets of 32 lottery tasks. Each questionnaire (odd and even row numbers in Appendix A) included four lottery pairs for each of 8 = 2 x 2 x 2 combinations of three within-subjects manipulations: worst-outcome difference (1/7 vs. 1/14 of omax) x worst-case probability difference (5% vs. 40%) x baseline winning probability (10% vs. 30% plus increments). The major dependent variable was the proportion of choices of the risky option (out of the 4 replications per condition), supplemented by ratings of the experienced difficulty of the decision and of an appropriate price to pay for the lottery.
Materials and procedure. Two independent computer-generated sets of 32 lottery tasks comprised the two forms of a questionnaire, both constructed according to the aforementioned generative rules but with different added random components and in different random order. Four lottery pairs were included on each page, each consisting of a tabular presentation of the lottery pair, a prompt to tick the preferred lottery, a pricing task prompted by the sentence “I would be willing to pay the following price for the chosen lottery ____ €”,4 and a five-point rating of how easy or difficult it was to choose A or B (1 = Very easy, 5 = very difficult). The original questionnaire format is present in Appendix B.
Instructions were provided on the cover page. A cover story mentioned that the research aimed at finding out how the attractiveness of lotteries can be increased. In particular, we were allegedly interested in whether the frustration of not winning can be ameliorated when the bad outcome is not zero but some smaller payoff that is still higher than zero. To help the researchers investigate this question, participants were asked to imagine fictitious horse-betting games, each one involving two horses. For each lottery task presented in the format of Appendix B, they had to tick a preferred horse, to indicate their willingness to pay for the lottery in Euro, and to indicate the experienced difficulty on a five-point scale.
Quality of judgments. For a first check on the reliability and regularity of the preference data, I examined the extent to which the 32 lottery tasks solicited similar responses from different judges, using an index of inter-judge agreement suggested by Rosenthal (1987). This index, which is comparable to Cronbach’s internal consistency, can vary between 0 and 1. It increases to the extent that there is little variance between decision makers in discriminating between lotteries. Inter-judge agreement was considerable (r = .73 and .79 for the two sets), testifying to the participants’ accuracy and motivation. Given this initial check on the quality of data, the present results cannot be discarded as due to noise or low motivation.
Figure 1: Mean proportions of risky choices (a), mean difficulty ratings (b), and mean pricing index (c) as a function of experimental conditions.
Lottery preferences. Let us now turn to the crucial question of whether the influences of the experimental manipulations on the lottery preferences support the PH predictions. For a suitable empirical measure, the number of A choices (i.e., choices of the risky alternative) per participant was computed for each of the eight within-subjects conditions, across all four tasks in each condition. Dividing these numbers by four resulted in convenient proportions, which can be called risky choice (RC) scores. These proportion scores were roughly normally distributed with homogeneous variance.
To recapitulate, the PH predicts that RC should be uniformly low for a worst-outcome difference of 1/7, when quick and conflictless step-1 decisions should produce unambivalent choices of the safer alternative, B. Only for an outcome difference of 1/14 should the PH allow for A choices, thus producing high RC scores. Note also that within the present design, the PH predicts always A choices when the worst-outcome difference is 1/14. This clear-cut prediction follows from two design features. Either in the 40% probability-difference condition, option B is too likely to yield its worst outcome in step 2. Or, if no choice is made in the 5% probability difference condition in step 2, step 3 will also lead to an A choice, because omaxA is maximal. In any case, in a three-factorial analysis of variance (ANOVA), the main effect of the worst-outcome difference factor represents a condensed test of all three PH predictions, all implying higher RC scores for the 1/14 than the 1/7 condition.
The PH does not predict any significant influence of the worst-case probability difference manipulation in the present design, because for a worst-outcome difference of 1/7 the probability difference should be bypassed anyway, and for 1/14 both probability differences should equally lead to A choices. Thus, any main effect or interaction involving the probability difference factor can only disconfirm the PH. (Notice that this prediction holds regardless of the probability-difference cutoff.) Similarly, any impact of the third factor, basic winning probability of the risky option, would contradict the PH. To the extent that this PH-irrelevant factor exerts a direct influence, or moderates the influence of other factors’, this could only disconfirm the PH.
A glance at Figure 1a, which displays mean RC as a function of experimental conditions, reveals a pattern that diverges from the PH predictions in many respects. Although a worst-outcome main effect, F(1,49) = 9.37, p < .01, reflects the predicted tendency for RC to increase from 1/7 to 1/14 outcome differences (Mean RC = .734 vs. .833), this tendency is restricted to small (5%) differences of worst-outcome probability (.611 vs. .721). It completely disappears for large (40%) probability differences (.875 vs. .880), as manifested in a worst-outcome x probability difference interaction, F(1,49) = 12.17, p < .01. This pattern is inconsistent with the assumed priority of worst outcomes over worst-outcome probabilities (regardless of the ratio between the worst-outcome difference and the maximum outcome, which the PH requires as a condition for using the worst outcome).
The secondary factor, difference in worst-outcome probability, produces a strong main effect, F(1,49) = 45.39, p < .001. The preference for the risky option A is clearly stronger when the worst-outcome probability difference favors A by 40% rather than only 5% (Mean RC = .878 vs. .666). This dominant effect is not nested within the small (1/14) worst-outcome difference (.880 vs. .760). The interaction (Figure 1a) shows that it is indeed stronger for large (1/7) differences (.875 vs. .611), contrary to the PH’s prediction that probability differences are ignored for worst-outcome differences exceeding 1/10 of the maximal outcome. (Again, this result does not depend on any assumption about the threshold for considering the worst-outcome difference.)
Finally, the main effect of the third factor, overall winning probability, is also significant, F(1,49) = 9.75, p < .01. Risky choices were more frequent for moderate winning chances of 30% (+ increments) than for small chances of 10% (+ increments). The corresponding difference in mean RC amounts to .814 versus .730. According to the PH, winning probabilities should be totally ignored. No other main effect or interaction was significant in the ANOVA of RC scores.
Altogether, this pattern diverges markedly from the core predictions derived from the PH model. The homogeneous main effect for the worst-outcome factor that the PH predicts for the present design was not obtained. Neither the PH’s assumption about the strictly sequential nature of the choice process nor the assumption of a strictly non-compensatory process, with only one cue operating at a time, can be reconciled with the present findings.
Consistency with PH predictions. Within each participant, a fit score was computed as the average proportion of choices consistent with the PH. The average fit score amounts to .526, hardly different from the chance rate of .50. A small standard deviation of only .103 suggests that this low fit holds for most individual participants. Forty-two of the 50 participants had fit scores between .40 and .60; only eight were above .60.5
Counting only difficult lotteries with EV ratios of maximally 1.2, as suggested by Brandstätter et al. (2008), the average fit score does not increase (M = .529).6 The number of participants whose fit score exceeds .50 is 29 (out of 50) for all lotteries and 31 for difficult lotteries with an EV ratio ≤ 1.2. The corresponding numbers for participants exceeding a fit of .65 is 3 and 5, respectively.7
Within participants, though, PH-consistent choices varied strongly as a function of experimental conditions (see Appendix A). A three-factorial ANOVA of the fit scores yielded a strong main effect for the worst-outcome difference, F(1,49) = 84.92, p < .001. PH fit was much lower in the 1/7 than in the 1/14 condition (.256 vs. .795). Apparently, this difference is due to the fact that the PH did not predict the relatively high rate of risky choices that were made even when the difference in worst outcomes exceeded 1/10 of the maximal outcome.
However, a strong worst-outcome difference x worst-case probability difference interaction, F(1,49) = 44.87, p < .001, indicates that the dependence of the PH fit on the first factor was greatly reduced when the probability difference was 5% (.388 vs. .715) rather than 40% (.125 vs. .875). The worst-outcome factor also interacted with the winning probability, F(1,48) = 9.62, p < .01; the impact of worst outcomes increased from low (10%) to moderate (30%) winning probability. The only other significant result was a main effect for the worst-case probability difference, F(1,49) = 11.33, p < .01, reflecting a higher PH fit for probability differences of 5% (.551) rather than 40% (.500). Thus, neither the absolute fit nor the relative differences of PH fit between task conditions lend support to the PH (see Appendix A).
Subjective difficulty. It is interesting to look at the ratings of subjective difficulty. A main effect for the worst-outcome difference in an ANOVA of the difficulty ratings, F(1,48) = 11.57, p < .01,8 shows that choices were experienced as more difficult when the worst-outcome difference decreased from 1/7 (M = 1.95) to 1/14 (M = 2.20), although the PH fit was higher for the latter condition. However, a worst-case probability difference main effect, F(1,48) = 7.53, p < .01, and a worst-outcome difference x probability difference interaction, F(1,48) = 7.51, p < .05, together preclude an interpretation of the worst-outcome main effect as a reflection of the number of process steps. Figure 1b shows that when the probability difference was low (5%) rather than high (40%), the worst-outcome influence on perceived difficulty disappeared completely (Figure 1b).9 I refrain from interpreting the three-way interaction, which was also significant, F(1,48) = 9.54, p < .01.
Willingness to Pay (WTP). Only 26 participants responded persistently to the WTP tasks. For these participants, I calculated a WTP index by multiplying the indicated price by +1 and –1 for A and B choices, respectively. Analogously to the RC index, the WTP index increases to the extent that WTP is higher for A than for B. The WTP ANOVA yielded only a significant main effects for the worst-case probability difference, F(1,25) = 7.06, p < .05, reflecting higher WTP when the probability difference was high (40%) rather than low (5%) (see Figure 1c). Across all 64 lottery items, the correlation between RC and WTP was r = .57.
On summary, the results obtained in the present experiment do not support the PH. Preferential choices between pairs of lotteries did not follow the PH’s three-step decision process that was captured by the three design factors. Although the PH model predicted only one dominant main effect for the worst-outcome difference between the two lotteries, this main effect was strongly moderated by other factors. The strongest result was due to the manipulation of the worst-case probability difference, pertaining to the second stage of the PH process. The impact of this manipulation was not confined to the weak (1/14) worst-outcome difference; it was actually enhanced for the strong (1/7) worst-outcome difference condition, in which the worst-case probability should play no role. Moreover, risky choices also increased as a function of increasing winning probabilities, which should be totally ignored. Altogether, then, this pattern is inconsistent with a sequentially ordered three-stage process, with only one cue being active at every stage. Neither the individual participants’ choices nor the average choices per decision item reached a satisfactory fit with the PH predictions.
One might argue that certain boundary conditions for the domain of the PH were not met. For instance, the PH may be confined to difficult choice problems with EV-ratios as low as maximally 1.2 (Brandstätter et al., 2008). Although this condition was not met for a subset of tasks, the remaining subset of lotteries with an EV ratio of maximally 1.2 yielded the same poor fit. Thus, in the context of 64 problems constructed to represent challenging conditions for the PH, the negative correlation between EV ratio and PH fit seems to disappear.
From a logical or psychological perspective, indeed, introducing such a restrictive EV assumption is highly unsatisfactory for two reasons. First, restricting the PH domain to nearly equal-EV gambles implies that compensation (of a high p by a low o and vice versa) is guaranteed by design. A strong test of the non-compensatory process assumption is not possible if the non-attended dimension (e.g., the p dimension when the focus is on o in the first stage) is not allowed to take values that produce discrepant EVs. And secondly, it is hard to understand why an EV must be determined as a precondition for the selection of a heuristic supposed to be much simpler and faster than EV calculation. Even when some proxy is used to estimate EV, rather than computing EV properly, the question is why the heuristic does not use that proxy but resorts instead to a refined three-stage algorithm.
One might also object that the PH is but one item from an adaptive toolbox containing many different heuristics. The failure of the PH under the present task conditions may mean only that some other heuristic was at work. However, while the adaptive toolbox affords an intriguing theoretical perspective, it has to go beyond the truism that many heuristics can explain many behaviors. It is rather necessary to figure out constraints on the operation of the PH. What conditions delimit the heuristic’s domain, and what behavioral outcomes does the underlying model exclude when the domain-specific conditions are met? Elaborating on these two kinds of constraints is essential for theoretical progress (Platt, 1964; Roberts & Pashler, 2000). Most findings obtained in the present study are of the kind that the PH model would exclude, even though the starting PH conditions were met in most of the lottery tasks. Although the EV ratio exceeded 1.2 in a small subset of tasks, the exclusion of these tasks did not increase the PH’s ability to account for the present decision data.
The purpose of the present study was to test critical implications of the PH. It was not designed to provide a comprehensive test of all alternative models, such as cumulative prospect theory (Tversky & Kahneman, 1992) or the transfer of attention exchange model (Birnbaum, 2008a). Again, an informed test of these models would have to rely on the controlled manipulation of distinct constraints imposed by these models, rather than the mere correlation of their predictions with the present data. Given the extended debate instigated by the PH (Birnbaum, 2008b; Johnson et al., 2008) and the attention it is receiving in decision research, its critical analysis should be a valuable research topic in its own right.
While I defend Popperian scrutiny as constructive and enlightening rather than merely sceptical, I hasten to add that the purpose of the present study has never been only to disconfirm a model as specific as the PH. It is rather motivated by general concerns about the manner in which heuristics as explanatory constructs should be tested. The PH is but a welcome example to illustrate this theoretical and methodological issue. It highlights the notion that rates of correct predictions do not afford an appropriate test of cognitive-process assumptions (Roberts & Pashler, 2000). If correspondence alone counts (i.e., the predictive success of a model across a range of applications), then we would have to accept that Clever Hans, the horse whose enumerative motor responses corresponded to the correct solution of arithmetic problems, was actually able to calculate, rather than using his owner’s subtle non-verbal signals (Pfungst, 1911). Just as explaining Clever Hans’ miracle required more than a correctness count, tests of heuristic models also call for manipulations of their critical features. If a heuristic is to explain the decision process, rather than only providing a paramorphic model (Hoffman, 1960), it is essential to test its distinct process features.
One problematic feature of the PH that I believe deserves to be discussed more openly is the overly strong assumption that only one cue is utilized at a time, in a strictly sequential order. Brunswik’s (1952) notion of vicarious functioning has told us that organisms flexibly change and combine the cues they are using, rather than always adhering to fixed sequential algorithms. Just as depth perception calls for a flexible use of different cues when it is dark rather than light, when one eye is closed, or when sound is available in addition to visual cues, the evaluation of preferences under risk need not obey any specific sequence of domain-unspecific cues, all in a strictly sequential order.
From the cognitive psychology of concept learning (Evans et al., 2003), and scientific hypothesis testing (Mynatt, Doherty, & Tweney, 1977), we know how difficult it is to verify a complex, conjunctive hypothesis. The PH postulates a sophisticated interplay of three specific cues, ordered in one and only one sequence, constrained to only one active cue at a time, applying an ominous 1/10 parameter as a stopping rule, and excluding all other cues. Logically, testing such a complex hypothesis means to exclude hundreds of alternative hypotheses that deviate from the PH in one or two or more aspects, or in countless combinations thereof. A research strategy that focuses on such complex concepts requires hundreds of parametrically organized studies to rule out alternative accounts.
Adaptive cognition is the ability to utilize and combine elementary cues in countless ways, depending on the requirements of the current situation. Organisms can quickly re-learn and invert vertical orientation when wearing mirror glasses (Kohler, 1956). They can reverse the fluency cue, learning that truth is associated with easy rather than difficult stimuli in a certain task context (Unkelbach, 2006). In priming experiments, they can learn to expect incongruent rather than congruent prime-target transitions. Given this amazing flexibility, or vicarious functioning, at the level of elementary cues, the question that suggests itself is what learning process – ontogenetic or phylogenetic — should support the acquisition of a strictly sequential, syntactically ordered cue utilization process that is restricted to one and only one cue, let alone the fundamental question of how singular cues can be distinguished from relational cues and interactions of multiple subordinate cues.
Raising these theoretical and logical questions is the ultimate purpose of the present paper. The PH is but a provocative exemplar of a research program that continues to fascinate psychologists, while at the same time reminding them of persisting theoretical and methodological problems.
Allais, M. (1979). The so-called Allais paradox and rational decisions under uncertainty. In M. Allais & O. Hagen (Eds.), Expected utility hypotheses and the Allais paradox (pp. 437–681). Dordrecht, the Netherlands: Reidel.
Ayal, S. & Hochman, G. (2009). Ignorance or integration: The cognitive processes underlying choice behavior. Journal of Behavioral Decision Making, 22, 455–474.
Birnbaum, M. (2008a). New tests of cumulative prospect theory and the priority heuristic: Probability-outcome tradeoff with branch splitting. Judgment and Decision Making, 3(4), 304–316.
Birnbaum, M. H. (2008b). Evaluation of the priority heuristic as a descriptive model of risky decision making: Comment on Brandstätter, Gigerenzer, and Hertwig (2006). Psychological Review, 115, 253–262.
Brandstätter, E., Gigerenzer, G., & Hertwig, R. (2006). The Priority Heuristic: Making choices without trade-offs. Psychological Review, 113, 409–432.
Brandstätter, E., Gigerenzer, G., & Hertwig, R. (2008). Risky choice with heuristics: Reply to Birnbaum (2008), Johnson, Schulte-Mecklenbeck, and Willemsen (2008), and Rieger and Wang (2008). Psychological Review, 115, 281–289.
Bröder, A., & Schiffer, S. (2003). Take The Best versus simultaneous feature matching: Probabilistic inferences from memory and effects of reprensentation format. Journal of Experimental Psychology: General, 132, 277–293.
Brunswik, E. (1952). Conceptual framework of psychology. Chicago, IL: University of Chicago Press.
Cosmides, L., & Tooby, J. (2006). Evolutionary psychology, moral heuristics, and the law. Heuristics and the law (pp. 175–205). Cambridge, MA Berlin USGermany: MIT Press.
Dougherty, M., Franco-Watkins, A., & Thomas, R. (2008). Psychological plausibility of the theory of probabilistic mental models and the fast and frugal heuristics. Psychological Review, 115, 199–211.
Evans, J. St. B. T., Clibbens, J., Cattani, A., Harris, A., & Dennis, I. (2003). Explicit and implicit processes in multicue judgement. Memory and Cognition, 31, 608–618.
Fiedler, K., Schmid, J., Kurzenhaeuser, S., & Schroeter, V. (2000). Lie detection as an attribution process: The anchoring effect revisited. In V. De Pascalis, V. Gheorghiu, P.W. Sheehan & I. Kirsch (Eds.). Suggestion and suggestibility: Advances in theory and research (pp. 113–136). Munich: M.E.G. Stiftung.
Gigerenzer, G., & Goldstein, D. (1996). Reasoning the fast and frugal way: Models of bounded rationality. Psychological Review, 103, 650–669.
Gigerenzer, G., Hoffrage, U., & Goldstein, D. (2008). Postscript: Fast and frugal heuristics. Psychological Review, 115, 238–239.
Gigerenzer, G., Todd, P. M., and the ABC group. (1999). Simple heuristics that make us smart. Evolution and cognition. New York, NY: Oxford University Press.
Gloeckner, A., & Betsch, T. (2008). Do people make decisions under risk based on ignorance? An empirical test of the priority heuristic against cumulative prospect theory. Organizational Behavior and Human Decision Processes, 107, 75–95.
Hilbig, B. E. (2008). One-reason decision making in risky choice? A closer look at the priority heuristic. Judgment and Decision Making, 3(6), 457–462.
Hilbig, B. E., & Pohl, R. F. (2008). Recognizing users of the recognition heuristic. Experimental Psychology, 55, 394–401.
Hoffman, P.J. (1960). The paramorphic representation of clinical judgment. Psychological Bulletin, 57, 116–131.
Johnson, E. J., Schulte-Mecklenbeck, M., & Willemsen, M. C. (2008). Process models deserve process data: Comment on Brandstätter, Gigerenzer, and Hertwig (2006). Psychological Review, 115, 263–272.
Katsikopoulos, K., Pachur, T., Machery, E., & Wallin, A. (2008). From Meehl to fast and frugal heuristics (and back): New insights into how to bridge the clinical-actuarial divide. Theory & Psychology, 18, 443–464.
Kohler, I. (1956). Der Brillenversuch in der Wahrnehmungspsychologie mit Bemerkungen zur Lehre von der Adaptation [The mirror glass experiment in perception psychology with comments on the study of adaptation]. Zeitschrift für Experimentelle und Angewandte Psychologie, 3, 381–417.
Lopes, L. L., & Oden, G. C. (1999). The role of aspiration level in risky choice: A comparison of cumulative prospect theory and SP/A theory. Journal of Mathematical Psychology, 43, 286–313.
Mynatt, C., Doherty, M., & Tweney, R. (1977). Confirmation bias in a simulated research environment: An experimental study of scientific inference. The Quarterly Journal of Experimental Psychology, 29, 85–95.
Newell, B. R., Rakow, T., Weston, N. J., & Shanks, D. R. (2004). Search strategies in decision making: The success of “success.” Journal of Behavioral Decision Making, 17, 117–137.
Platt, J. R. (1964). Strong inference. Science, 146, 347–353.
Pfungst, O. (1911). Clever Hans. New York: Holt.
Rieskamp, J. (2008). The probabilistic nature of preferential choice. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34, 1446–1465.
Rieskamp, J., & Otto, P. (2006). SSL: A theory of how people learn to select strategies. Journal of Experimental Psychology: General, 135, 207–236.
Roberts, S., & Pashler, H. (2000). How persuasive is a good fit? A comment on theory testing. Psychological Review, 107, 358–367.
Rosenthal, R. (1987). Judgment studies: Design, analysis, and meta-analysis. New York: Cambridge University Press.
Schwarz, N., Bless, H., Strack, F., Klumpp, G., Rittenauer-Schatka, H., & Simons, A. (1991). Ease of retrieval as information: Another look at the availability heuristic. Journal of Personality and Social Psychology, 61, 195–202.
Simon, H. A. (1983). Reason in human affairs. Stanford, CA: Stanford University Press.
Todd, P. (2000). The ecological rationality of mechanisms evolved to make up minds. American Behavioral Scientist, 43, 940–956.
Tversky, A., & Kahneman, D. (1973). Availability: A heuristic for judging frequency and probability. Cognitive Psychology, 5, 207–232.
Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science, 185, 1124–1131.
Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5, 297–323.
Unkelbach, C. (2006). The learned interpretation of cognitive fluency. Psychological Science, 17, 339–345.
Wänke, M., & Bless. H. (2000). How ease of retrieval may affect attitude judgments. In H. Bless & J. Forgas (Eds.) The role of subjective states in social cognition and behavior (pp. 143–161). New York: Psychology Press.
| Risky option A | Conservative option B | ||||||||||||||
| p(omax) | omax | p(omin) | omin | p(omax) | omax | p(omin) | omin | 1st EV | 2nd EV | EV-Ratio | (A choice) | (PHcorrect) | |||
| PH predicts B o-diff = 1/7 p-diff = 5% p(omax) = 10 + Increments | |||||||||||||||
| 16 | 84 | 84 | 22 | 11 | 54 | 89 | 34 | 31.92 | 36.20 | 1.13 | 0.72 | 0.28 | |||
| 19 | 49 | 81 | 28 | 14 | 39 | 86 | 35 | 31.99 | 35.56 | 1.11 | 0.36 | 0.64 | |||
| 21 | 504 | 79 | 18 | 16 | 101 | 84 | 90 | 120.06 | 91.76 | 1.31 | 0.58 | 0.40 | |||
| 21 | 476 | 79 | 15 | 16 | 86 | 84 | 83 | 111.81 | 83.48 | 1.34 | 0.52 | 0.48 | |||
| 17 | 126 | 83 | 81 | 12 | 103 | 88 | 99 | 88.65 | 99.48 | 1.12 | 0.72 | 0.28 | |||
| 17 | 126 | 83 | 81 | 12 | 103 | 88 | 99 | 88.65 | 99.48 | 1.12 | 0.60 | 0.40 | |||
| 21 | 224 | 79 | 38 | 16 | 122 | 84 | 70 | 77.06 | 78.32 | 1.02 | 0.67 | 0.32 | |||
| 23 | 196 | 77 | 38 | 18 | 113 | 82 | 66 | 74.34 | 74.46 | 1.00 | 0.48 | 0.52 | |||
| PH predicts B o-diff = 1/7 p-diff = 40% p(omax) = 10 + Increments | |||||||||||||||
| 55 | 63 | 45 | 25 | 15 | 46 | 85 | 34 | 45.90 | 35.80 | 1.28 | 0.96 | 0.04 | |||
| 53 | 98 | 47 | 26 | 13 | 64 | 87 | 40 | 64.16 | 43.12 | 1.49 | 0.72 | 0.28 | |||
| 56 | 434 | 44 | 20 | 16 | 106 | 84 | 82 | 251.84 | 85.84 | 2.93 | 0.92 | 0.08 | |||
| 59 | 462 | 41 | 18 | 19 | 99 | 81 | 84 | 279.96 | 86.85 | 3.22 | 0.84 | 0.16 | |||
| 54 | 126 | 46 | 82 | 14 | 103 | 86 | 100 | 105.76 | 100.42 | 1.05 | 0.76 | 0.24 | |||
| 57 | 126 | 43 | 81 | 17 | 103 | 83 | 99 | 106.65 | 99.68 | 1.07 | 0.76 | 0.24 | |||
| 50 | 196 | 50 | 35 | 10 | 109 | 90 | 63 | 115.50 | 67.60 | 1.71 | 0.92 | 0.08 | |||
| 55 | 231 | 45 | 33 | 15 | 116 | 85 | 66 | 141.90 | 73.50 | 1.93 | 0.80 | 0.20 | |||
| PH predicts B o-diff = 1/7 p-diff = 5% p(omax) = 30 + Increments | |||||||||||||||
| 44 | 119 | 56 | 22 | 39 | 67 | 61 | 39 | 64.68 | 49.92 | 1.30 | 0.72 | 0.28 | |||
| 35 | 77 | 65 | 23 | 30 | 52 | 70 | 34 | 41.90 | 39.40 | 1.06 | 0.44 | 0.56 | |||
| 40 | 476 | 60 | 17 | 35 | 95 | 65 | 85 | 200.60 | 88.50 | 2.27 | 0.88 | 0.12 | |||
| 39 | 462 | 61 | 16 | 34 | 90 | 66 | 82 | 189.94 | 84.72 | 2.24 | 0.72 | 0.28 | |||
| 36 | 126 | 64 | 82 | 31 | 103 | 69 | 100 | 97.84 | 100.93 | 1.03 | 0.48 | 0.52 | |||
| 38 | 126 | 62 | 81 | 33 | 103 | 67 | 99 | 98.10 | 100.32 | 1.02 | 0.52 | 0.48 | |||
| 44 | 189 | 56 | 38 | 39 | 110 | 61 | 65 | 104.44 | 82.55 | 1.27 | 0.80 | 0.20 | |||
| 38 | 182 | 62 | 38 | 33 | 108 | 67 | 64 | 92.72 | 78.52 | 1.18 | 0.56 | 0.44 | |||
| PH predicts B o-diff = 1/7 p-diff = 40% p(omax) = 30 + Increments | |||||||||||||||
| 77 | 105 | 23 | 25 | 37 | 66 | 63 | 40 | 86.60 | 49.62 | 1.75 | 0.92 | 0.08 | |||
| 72 | 63 | 28 | 27 | 32 | 47 | 68 | 36 | 52.92 | 39.52 | 1.34 | 0.88 | 0.12 | |||
| 72 | 448 | 28 | 19 | 32 | 103 | 68 | 83 | 327.88 | 89.40 | 3.67 | 0.92 | 0.08 | |||
| 73 | 469 | 27 | 20 | 33 | 108 | 67 | 87 | 347.77 | 93.93 | 3.70 | 0.84 | 0.16 | |||
| 78 | 126 | 22 | 82 | 38 | 103 | 62 | 100 | 116.32 | 101.14 | 1.15 | 0.96 | 0.04 | |||
| 73 | 133 | 27 | 81 | 33 | 108 | 67 | 100 | 118.96 | 102.64 | 1.16 | 0.96 | 0.04 | |||
| 70 | 175 | 30 | 38 | 30 | 106 | 70 | 63 | 133.90 | 75.90 | 1.76 | 0.96 | 0.04 | |||
| 75 | 231 | 25 | 36 | 35 | 121 | 65 | 69 | 182.25 | 87.20 | 2.09 | 0.88 | 0.12 | |||
| Note: Odd and even row numbers represent the two questionnaire versions. | |||||||||||||||
| Risky option A | Conservative option B | ||||||||||||||
| p(omax) | omax | p(omin) | omin | p(omax) | omax | p(omin) | omin | 1st EV | 2nd EV | EV-Ratio | (A choice) | (PHcorrect) | |||
| PH predicts A o-diff = 1/14 p-diff = 5% p(omax) = 10 + Increments | |||||||||||||||
| 23 | 196 | 77 | 26 | 18 | 127 | 82 | 40 | 65.10 | 55.66 | 1.17 | 0.76 | 0.76 | |||
| 17 | 224 | 83 | 21 | 12 | 127 | 88 | 37 | 55.51 | 47.80 | 1.16 | 0.52 | 0.52 | |||
| 21 | 854 | 79 | 20 | 16 | 211 | 84 | 81 | 195.14 | 101.80 | 1.92 | 0.70 | 0.64 | |||
| 21 | 1008 | 79 | 17 | 16 | 193 | 84 | 89 | 225.11 | 105.64 | 2.13 | 0.64 | 0.64 | |||
| 24 | 196 | 76 | 85 | 19 | 168 | 81 | 99 | 111.64 | 112.11 | 1.00 | 0.76 | 0.76 | |||
| 17 | 182 | 83 | 81 | 12 | 157 | 88 | 94 | 98.17 | 101.56 | 1.03 | 0.60 | 0.60 | |||
| 20 | 378 | 80 | 40 | 15 | 226 | 85 | 67 | 107.60 | 90.85 | 1.18 | 0.68 | 0.68 | |||
| 15 | 462 | 85 | 33 | 10 | 231 | 90 | 66 | 97.35 | 82.50 | 1.18 | 0.60 | 0.60 | |||
| PH predicts A o-diff = 1/14 p-diff = 40% p(omax) = 10 + Increments | |||||||||||||||
| 52 | 154 | 48 | 21 | 12 | 101 | 88 | 32 | 90.16 | 40.28 | 2.24 | 0.96 | 0.96 | |||
| 50 | 252 | 50 | 21 | 10 | 136 | 90 | 39 | 136.50 | 48.70 | 2.80 | 0.84 | 0.84 | |||
| 58 | 896 | 42 | 17 | 18 | 188 | 82 | 81 | 526.82 | 100.26 | 5.25 | 0.92 | 0.92 | |||
| 51 | 1036 | 49 | 15 | 11 | 175 | 89 | 89 | 535.71 | 98.46 | 5.44 | 0.72 | 0.72 | |||
| 56 | 154 | 44 | 88 | 16 | 137 | 84 | 99 | 124.96 | 105.08 | 1.19 | 0.88 | 0.84 | |||
| 53 | 112 | 47 | 84 | 13 | 102 | 87 | 92 | 98.84 | 93.30 | 1.06 | 0.72 | 0.72 | |||
| 58 | 476 | 42 | 32 | 18 | 231 | 82 | 66 | 289.52 | 95.70 | 3.03 | 0.96 | 0.96 | |||
| 52 | 364 | 48 | 40 | 12 | 221 | 88 | 66 | 208.48 | 84.60 | 2.46 | 0.76 | 0.76 | |||
| PH predicts A o-diff = 1/14 p-diff = 5% p(omax) = 30 + Increments | |||||||||||||||
| 35 | 112 | 65 | 24 | 30 | 84 | 70 | 32 | 54.80 | 47.60 | 1.15 | 0.96 | 0.92 | |||
| 43 | 154 | 57 | 24 | 38 | 106 | 62 | 35 | 79.90 | 61.98 | 1.29 | 0.72 | 0.72 | |||
| 41 | 1092 | 59 | 12 | 36 | 146 | 64 | 90 | 454.80 | 110.16 | 4.13 | 0.84 | 0.84 | |||
| 40 | 1022 | 60 | 13 | 35 | 154 | 65 | 86 | 416.60 | 109.80 | 3.79 | 0.64 | 0.64 | |||
| 41 | 196 | 59 | 81 | 36 | 167 | 64 | 95 | 128.15 | 120.92 | 1.06 | 0.88 | 0.88 | |||
| 38 | 112 | 62 | 85 | 33 | 102 | 67 | 93 | 95.26 | 95.97 | 1.01 | 0.56 | 0.56 | |||
| 40 | 434 | 60 | 31 | 35 | 217 | 65 | 62 | 192.20 | 116.25 | 1.65 | 0.84 | 0.84 | |||
| 44 | 434 | 56 | 34 | 39 | 227 | 61 | 65 | 210.00 | 128.18 | 1.64 | 0.84 | 0.84 | |||
| PH predicts A o-diff = 1/14 p-diff = 40% p(omax) = 30 + Increments | |||||||||||||||
| 72 | 168 | 28 | 25 | 32 | 114 | 68 | 37 | 127.96 | 61.64 | 2.08 | 1.00 | 1.00 | |||
| 78 | 70 | 22 | 26 | 38 | 59 | 62 | 31 | 60.32 | 41.64 | 1.45 | 0.96 | 0.96 | |||
| 78 | 938 | 22 | 19 | 38 | 207 | 62 | 86 | 735.82 | 131.98 | 5.58 | 0.88 | 0.88 | |||
| 76 | 952 | 24 | 19 | 36 | 208 | 64 | 87 | 728.08 | 130.56 | 5.58 | 0.88 | 0.88 | |||
| 76 | 126 | 24 | 84 | 36 | 114 | 64 | 93 | 115.92 | 100.56 | 1.15 | 0.96 | 0.92 | |||
| 77 | 238 | 23 | 83 | 37 | 198 | 63 | 100 | 202.35 | 136.26 | 1.49 | 0.80 | 0.80 | |||
| 79 | 378 | 21 | 35 | 39 | 213 | 61 | 62 | 305.97 | 120.89 | 2.53 | 0.92 | 0.92 | |||
| 77 | 448 | 23 | 36 | 37 | 237 | 63 | 68 | 353.24 | 130.53 | 2.71 | 0.92 | 0.92 | |||
| Note: Odd and even row numbers represent the two questionnaire versions. | |||||||||||||||
| Please tick A or B | Probability of winning | Payoff in case of winning | Probability of not winning | Payoff in case of not winning |
| □ Horse A | 39% | 227 € | 61% | 65 € |
| □ Horse B | 44% | 434 € | 56% | 34 € |
| I am willing to pay the following price for participation: _____ € How easy or difficult was it to make a choice for either A or B? Very easy 1 2 3 4 5 Very difficult |
Outcome difference 1/14 Probability difference 5% Basic winning probabilities .3 Basic not-winning payoff 30 60 | |||
| Please tick A or B | Probability of winning | Payoff in case of winning | Probability of not winning | Payoff in case of not winning |
| □ Horse A | 18% | 113 € | 82% | 66 € |
| □ Horse B | 23% | 196 € | 77% | 38 € |
| I am willing to pay the following price for participation: _____ € How easy or difficult was it to make a choice for either A or B? Very easy 1 2 3 4 5 Very difficult |
Outcome difference 1/7 Probability difference 5% Basic winning probabilities .1 Basic not-winning payoff 10 80 | |||
| Please tick A or B | Probability of winning | Payoff in case of winning | Probability of not winning | Payoff in case of not winning |
| □ Horse A | 55% | 63 € | 45% | 25 € |
| □ Horse B | 15% | 46 € | 85% | 34 € |
| I am willing to pay the following price for participation: _____ € How easy or difficult was it to make a choice for either A or B? Very easy 1 2 3 4 5 Very difficult |
Outcome difference 1/7 Probability difference 40% Basic winning probabilities .1 Basic not-winning payoff 20 30 | |||
| Please tick A or B | Probability of winning | Payoff in case of winning | Probability of not winning | Payoff in case of not winning |
| □ Horse A | 37% | 198 € | 63% | 100 € |
| □ Horse B | 77% | 238 € | 23% | 83 € |
| I am willing to pay the following price for participation: _____ € How easy or difficult was it to make a choice for either A or B? Very easy 1 2 3 4 5 Very difficult |
Outcome difference 1/14 Probability difference 40% Basic winning probabilities .3 Basic not-winning payoff 80 90 | |||
Note: The horse labels “A”
and “B” should not be confused
with the labels used to denote the risky and conservative lottery in
the text. The presented questionnaire did not include the parameter
boxes on the right.
This document was translated from LATEX by HEVEA.